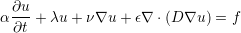
The ADRSolver is designed to solve partial differential equations of the form:
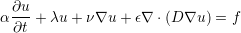 | (4.1) |
in either discontinuous or continuous projections of the solution field. For a full list of the equations which are supported, and the capabilities of each equation, see the table below.
| Equation to solve | EquationType | Dimensions | Projections |
| ∇2u = 0 | Laplace | All | Continuous/Discontinuous |
| ∇2u = f | Poisson | All | Continuous/Discontinuous |
| ∇2u + λu = f | Helmholtz | All | Continuous/Discontinuous |
| ϵ∇2u + V∇u = f | SteadyAdvectionDiffusion | 2D only | Continuous/Discontinuous |
| ϵ∇2u + λu = f | SteadyDiffusionReaction | 2D only | Continuous/Discontinuous |
| ϵ∇2uV∇u + λu = f | SteadyAdvectionDiffusionReaction | 2D only | Continuous/Discontinuous |
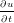 + V∇u = f + V∇u = f | UnsteadyAdvection | All | Continuous/Discontinuous |
 = ϵ∇2u = ϵ∇2u | UnsteadyDiffusion | All | Continuous/Discontinuous |
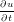 + V∇u = ϵ∇2u + V∇u = ϵ∇2u | UnsteadyAdvectionDiffusion | All | Continuous/Discontinuous |
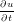 + u∇u = 0 + u∇u = 0 | UnsteadyInviscidBurger | 1D only | Continuous/Discontinuous |