15.1 Fundamental Theories of CompressibleFlowSolver

15.1.1 Governing equations

The governing compressible Navier-Stokes equations, representing conservation of mass, momentum and energy, can be written in abridged form as

(15.1)

where L is the analytical nonlinear spatial operator, U is the vector of conservative variables, F = F(U) is the inviscid flux and G = G(U,∇U) is the viscous flux.

15.1.2 Discretization

Spatial discretization

Various spatial discretization methods are supported, for example the WeakDG and FR for advection term, LDG and IP methods for the diffusion term. Here, we take the weakDG as example. The computational domain (Ω) is divided into N_e non-overlapping elements (Ω_e). The weak form of Eqs. (15.1) is obtained by multiplying the test function ϕ_p and performing integration by parts in Ω_e,

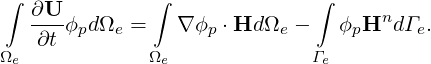(15.2)

The fluxes are calculated at some quadrature points and a quadrature rule with N_Q quadrature points is adopted to calculate the integration in the element and N_Q^Γ quadrature points on element boundaries. This leads to

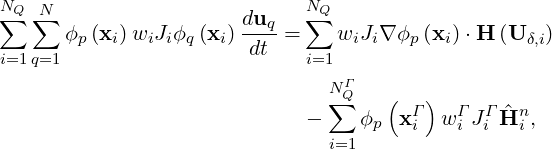(15.3)

where u_q is the coefficient vector of the basis function. The whole discretization can be written in the following matrix form

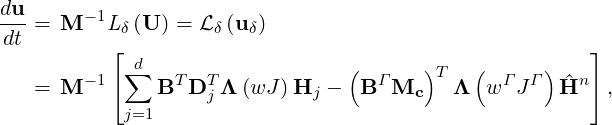(15.4)

where d is the spatial dimension, M = B^T Λ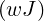B is the mass matrix, Λ represents a diagonal matrix, D_j is the derivative matrix in the jth direction, B^Γ is the backward transformation matrix of ϕ^Γ and M_c is the mapping matrix between ϕ^Γ and ϕ, J is the interpolation matrix from quadrature points of a element to quadrature points of its element boundaries.

The weak DG scheme for the advection term is complete as long as a Riemann numerical flux is used to calculate the normal flux, 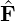ⁿ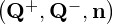, in which Q⁺ and Q^- are variable values on the exterior and interior sides of the element boundaries, respectively. Similarly, LDG or IP methods are needed to provide the numerical fluxes on element boundaries for the diffusion terms.

Time discretization

Various multi-step and multi-stage methods have been implemented in an object-oriented general linear methods framework. Here, the Runge-Kutta methods are took as examples. The ith stage of the Runge-Kutta method is

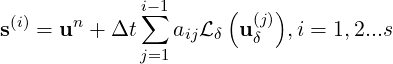(15.5)

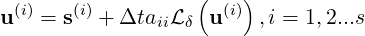(15.6)

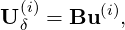(15.7)

where a_ij is the coefficient of the Runge-Kutta method, s is a source term, B is the backward transform matrix. Finally, the solution of the new time step (n + 1) is calculated by

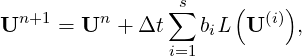(15.8)

For explicit RK methods, a_ii = 0, the discretization is complete and straightforward.

Jacobian-free Newton-Krylov method

Eq. (15.6) of the implicit stages (a_ii≠0) can be written as the nonlinear system

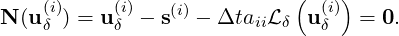(15.9)

This system is iteratively solved by Newton’s method [49] with the Newton step, Δv = v^k+1 -v^k, updated through the solution of the linear system

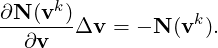(15.10)

where v⁰ = s⁽ⁱ⁾ is adopted as an initial guess. When the Newton residual is smaller than the convergence tolerance of the Newton iterations τ, which is

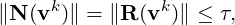(15.11)

u_it⁽ⁱ⁾ = v^k is regarded as the approximate solution of the nonlinear system, where R is the remaining Newton residual vector N(u_it⁽ⁱ⁾) after convergence.

The restarted generalized minimal residual method (GMRES) [60] is used for solving the linear problem (15.10). The Jacobian matrix and vector inner product operator is approximated by the following finite difference

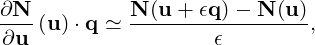(15.12)

where ϵ is the step size of the finite difference approximation.

The use of good preconditioners in GMRES is very important for efficiently solving stiff linear systems. Instead of solving the system of Eq. (15.10) directly, one can get the same solution by solving the preconditioned linear system

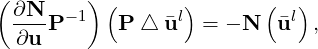(15.13)

where P is the preconditioning matrix. A low memory block relaxed Jacobi iterative preconditioner is implemented.