|
Nektar++
|
|
Nektar++
|
Go to the source code of this file.
Namespaces | |
| namespace | Polylib |
| The namespace associated with the the Polylib library (Polylib introduction) | |
Macros | |
| #define | STOP 30 |
| Maximum number of iterations in polynomial defalation routine Jacobz. | |
| #define | EPS 100*DBL_EPSILON |
| Precision tolerance for two points to be similar. | |
| #define | sign(a, b) ((b)<0 ? -fabs(a) : fabs(a)) |
| return the sign(b)*a | |
| #define | POLYNOMIAL_DEFLATION 0 |
| Define whether to use polynomial deflation (1) or tridiagonal solver (0). | |
| #define | jacobz(n, z, alpha, beta) Jacobz(n,z,alpha,beta) |
| zero determination using Newton iteration with polynomial deflation | |
Functions | |
| static void | Polylib::Jacobz (const int n, double *z, const double alpha, const double beta) |
| Calculate the n zeros, z, of the Jacobi polynomial, i.e. | |
| static void | Polylib::TriQL (const int n, double *d, double *e, double **z) |
| QL algorithm for symmetric tridiagonal matrix. | |
| double | Polylib::gammaF (const double x) |
Calculate the Gamma function , 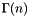 , for integer. , for integer. | |
| static void | Polylib::RecCoeff (const int n, double *a, double *b, const double alpha, const double beta) |
| The routine finds the recurrence coefficients a and. | |
| void | Polylib::JKMatrix (int n, double *a, double *b) |
| Calcualtes the Jacobi-kronrod matrix by determining the. | |
| void | Polylib::chri1 (int n, double *a, double *b, double *a0, double *b0, double z) |
Given a weight function 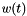 through the first n+1. through the first n+1. | |
| void | Polylib::zwgj (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Jacobi zeros and weights. | |
| void | Polylib::zwgrjm (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Radau-Jacobi zeros and weights with end point at z=-1. | |
| void | Polylib::zwgrjp (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Radau-Jacobi zeros and weights with end point at z=1. | |
| void | Polylib::zwglj (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1. | |
| void | Polylib::zwgk (double *z, double *w, const int npt, const double alpha, const double beta) |
| Gauss-Kronrod-Jacobi zeros and weights. | |
| void | Polylib::zwrk (double *z, double *w, const int npt, const double alpha, const double beta) |
| Gauss-Radau-Kronrod-Jacobi zeros and weights. | |
| void | Polylib::zwlk (double *z, double *w, const int npt, const double alpha, const double beta) |
| Gauss-Lobatto-Kronrod-Jacobi zeros and weights. | |
| void | Polylib::Dgj (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix and its transpose associated. | |
| void | Polylib::Dgrjm (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix and its transpose associated. | |
| void | Polylib::Dgrjp (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix associated with the. | |
| void | Polylib::Dglj (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix associated with the. | |
| double | Polylib::hgj (const int i, const double z, const double *zgj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through. | |
| double | Polylib::hgrjm (const int i, const double z, const double *zgrj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through the. | |
| double | Polylib::hgrjp (const int i, const double z, const double *zgrj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through the. | |
| double | Polylib::hglj (const int i, const double z, const double *zglj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through the. | |
| void | Polylib::Imgj (double *im, const double *zgj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Jacobi points to an. | |
| void | Polylib::Imgrjm (double *im, const double *zgrj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Radau-Jacobi points. | |
| void | Polylib::Imgrjp (double *im, const double *zgrj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Radau-Jacobi points. | |
| void | Polylib::Imglj (double *im, const double *zglj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Lobatto-Jacobi points. | |
| void | Polylib::jacobfd (const int np, const double *z, double *poly_in, double *polyd, const int n, const double alpha, const double beta) |
Routine to calculate Jacobi polynomials, 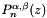 , and their first derivative, , and their first derivative, 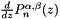 . . | |
| void | Polylib::jacobd (const int np, const double *z, double *polyd, const int n, const double alpha, const double beta) |
| Calculate the derivative of Jacobi polynomials. | |
| void | Polylib::JacZeros (const int n, double *a, double *b, const double alpha, const double beta) |
| Zero and Weight determination through the eigenvalues and eigenvectors of a tridiagonal. | |
| #define EPS 100*DBL_EPSILON |
Precision tolerance for two points to be similar.
Definition at line 18 of file Polylib.cpp.
Referenced by Polylib::hgj(), Polylib::hglj(), Polylib::hgrjm(), Polylib::hgrjp(), and Polylib::Jacobz().
| #define jacobz | ( | n, | |
| z, | |||
| alpha, | |||
| beta | |||
| ) | Jacobz(n,z,alpha,beta) |
zero determination using Newton iteration with polynomial deflation
Definition at line 40 of file Polylib.cpp.
Referenced by Polylib::zwgj(), Polylib::zwglj(), Polylib::zwgrjm(), and Polylib::zwgrjp().
| #define POLYNOMIAL_DEFLATION 0 |
Define whether to use polynomial deflation (1) or tridiagonal solver (0).
Definition at line 32 of file Polylib.cpp.
| #define sign | ( | a, | |
| b | |||
| ) | ((b)<0 ? -fabs(a) : fabs(a)) |
return the sign(b)*a
Definition at line 22 of file Polylib.cpp.
Referenced by Nektar::LocalRegions::Expansion2D::AddEdgeBoundaryInt(), Nektar::LocalRegions::Expansion2D::AddHDGHelmholtzEdgeTerms(), Nektar::MultiRegions::AssemblyMap::AssemblyMap(), Nektar::MultiRegions::GlobalLinSysStaticCond::ConstructNextLevelCondensedSystem(), Nektar::StdRegions::StdExpansion::CreateIndexMap(), Nektar::MultiRegions::PreconditionerLowEnergy::CreateMultiplicityMap(), Nektar::LibUtilities::functions::functions(), Nektar::MultiRegions::ContField3D::GenerateDirBndCondForcing(), Nektar::Extrapolate::GenerateHOPBCMap(), Nektar::LocalRegions::Expansion2D::GetPhysEdgeVarCoeffsFromElement(), main(), Nektar::MultiRegions::PatchMap::SetPatchMap(), Polylib::TriQL(), Nektar::LocalRegions::Expansion2D::v_AddRobinEdgeContribution(), Nektar::LocalRegions::Expansion3D::v_AddRobinMassMatrix(), Nektar::LocalRegions::Expansion2D::v_AddRobinMassMatrix(), Nektar::MultiRegions::ContField3D::v_FillBndCondFromField(), Nektar::MultiRegions::ContField2D::v_FillBndCondFromField(), Nektar::StdRegions::StdQuadExp::v_FwdTrans_BndConstrained(), Nektar::LocalRegions::TriExp::v_FwdTrans_BndConstrained(), Nektar::LocalRegions::QuadExp::v_FwdTrans_BndConstrained(), Nektar::StdRegions::StdTriExp::v_FwdTrans_BndConstrained(), Nektar::LocalRegions::Expansion3D::v_GenMatrix(), Nektar::LocalRegions::Expansion2D::v_GenMatrix(), Nektar::MultiRegions::ContField3D::v_HelmSolve(), Nektar::MultiRegions::ContField3D::v_ImposeDirichletConditions(), Nektar::MultiRegions::ContField2D::v_ImposeDirichletConditions(), Nektar::MultiRegions::ExpListHomogeneous2D::v_PhysDeriv(), Nektar::MultiRegions::ExpListHomogeneous1D::v_PhysDeriv(), Nektar::LaxFriedrichsSolver::v_PointSolve(), and Nektar::LaxFriedrichsSolver::v_PointSolveVisc().
| #define STOP 30 |
Maximum number of iterations in polynomial defalation routine Jacobz.
Definition at line 14 of file Polylib.cpp.
Referenced by Polylib::Jacobz(), and Polylib::TriQL().
 1.8.1.2
1.8.1.2