|
Nektar++
|
|
Nektar++
|
Calculation and storage of geometric factors associated with the mapping from StdRegions reference elements to a given LocalRegions physical element in the mesh. More...
#include <GeomFactors.h>
Public Member Functions | |
| GeomFactors (const GeomType gtype, const int coordim, const StdRegions::StdExpansionSharedPtr &xmap, const Array< OneD, Array< OneD, NekDouble > > &coords) | |
| Constructor for GeomFactors class. More... | |
| GeomFactors (const GeomFactors &S) | |
| Copy constructor. More... | |
| ~GeomFactors () | |
| Destructor. More... | |
| DerivStorage | GetDeriv (const LibUtilities::PointsKeyVector &keyTgt) |
Return the derivative of the mapping with respect to the reference coordinates, 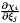 . More... . More... | |
| const Array< OneD, const NekDouble > | GetJac (const LibUtilities::PointsKeyVector &keyTgt) |
| Return the Jacobian of the mapping and cache the result. More... | |
| const Array< TwoD, const NekDouble > | GetGmat (const LibUtilities::PointsKeyVector &keyTgt) |
Return the Laplacian coefficients 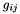 . More... . More... | |
| const Array< TwoD, const NekDouble > | GetDerivFactors (const LibUtilities::PointsKeyVector &keyTgt) |
Return the derivative of the reference coordinates with respect to the mapping, 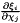 . More... . More... | |
| GeomType | GetGtype () |
| Returns whether the geometry is regular or deformed. More... | |
| bool | IsValid () const |
| Determine if element is valid and not self-intersecting. More... | |
| int | GetCoordim () const |
| Return the number of dimensions of the coordinate system. More... | |
| size_t | GetHash () |
| Computes a hash of this GeomFactors element. More... | |
Protected Member Functions | |
| StdRegions::StdExpansionSharedPtr & | GetXmap () |
| Return the Xmap;. More... | |
Protected Attributes | |
| GeomType | m_type |
| Type of geometry (e.g. eRegular, eDeformed, eMovingRegular). More... | |
| int | m_expDim |
| Dimension of expansion. More... | |
| int | m_coordDim |
| Dimension of coordinate system. More... | |
| bool | m_valid |
| Validity of element (Jacobian positive) More... | |
| StdRegions::StdExpansionSharedPtr | m_xmap |
| Stores information about the expansion. More... | |
| Array< OneD, Array< OneD, NekDouble > > | m_coords |
| Stores coordinates of the geometry. More... | |
| std::map< LibUtilities::PointsKeyVector, Array< OneD, NekDouble > > | m_jacCache |
| Jacobian vector cache. More... | |
| std::map< LibUtilities::PointsKeyVector, Array< TwoD, NekDouble > > | m_derivFactorCache |
| DerivFactors vector cache. More... | |
Private Member Functions | |
| void | CheckIfValid () |
| Tests if the element is valid and not self-intersecting. More... | |
| DerivStorage | ComputeDeriv (const LibUtilities::PointsKeyVector &keyTgt) const |
| Array< OneD, NekDouble > | ComputeJac (const LibUtilities::PointsKeyVector &keyTgt) const |
| Return the Jacobian of the mapping and cache the result. More... | |
| Array< TwoD, NekDouble > | ComputeGmat (const LibUtilities::PointsKeyVector &keyTgt) const |
Computes the Laplacian coefficients 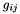 . More... . More... | |
| Array< TwoD, NekDouble > | ComputeDerivFactors (const LibUtilities::PointsKeyVector &keyTgt) const |
Return the derivative of the reference coordinates with respect to the mapping, 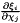 . More... . More... | |
| void | Interp (const LibUtilities::PointsKeyVector &src_points, const Array< OneD, const NekDouble > &src, const LibUtilities::PointsKeyVector &tgt_points, Array< OneD, NekDouble > &tgt) const |
| Perform interpolation of data between two point distributions. More... | |
| void | Adjoint (const Array< TwoD, const NekDouble > &src, Array< TwoD, NekDouble > &tgt) const |
| Compute the transpose of the cofactors matrix. More... | |
Friends | |
| bool | operator== (const GeomFactors &lhs, const GeomFactors &rhs) |
| Tests if two GeomFactors classes are equal. More... | |
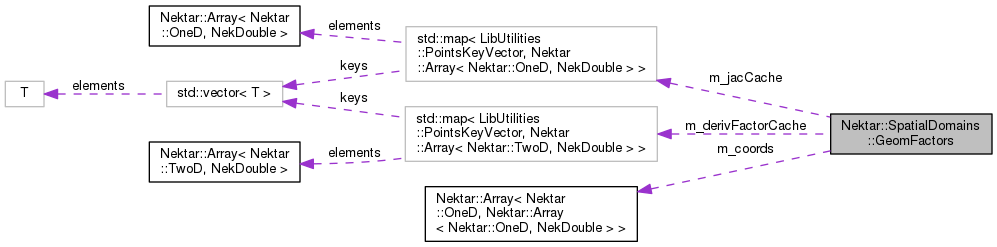
Calculation and storage of geometric factors associated with the mapping from StdRegions reference elements to a given LocalRegions physical element in the mesh.
This class stores the various geometric factors associated with a specific element, necessary for fundamental integration and differentiation operations as well as edge and surface normals.
Initially, these algorithms are provided with a mapping from the reference region element to the physical element. Practically, this is represented using a corresponding reference region element for each coordinate component. Note that for straight-sided elements, these elements will be of linear order. Curved elements are represented using higher-order coordinate mappings. This geometric order is in contrast to the order of the spectral/hp expansion order on the element.
For application of the chain rule during differentiation we require the partial derivatives
![\[\frac{\partial \xi_i}{\partial \chi_j}\]](form_200.png)
evaluated at the physical points of the expansion basis. We also construct the inverse metric tensor 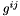 which, in the case of a domain embedded in a higher-dimensional space, supports the conversion of covariant quantities to contravariant quantities. When the expansion dimension is equal to the coordinate dimension the Jacobian of the mapping
which, in the case of a domain embedded in a higher-dimensional space, supports the conversion of covariant quantities to contravariant quantities. When the expansion dimension is equal to the coordinate dimension the Jacobian of the mapping 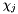 is a square matrix and consequently the required terms are the entries of the inverse of the Jacobian. However, in general this is not the case, so we therefore implement the construction of these terms following the derivation in Cantwell, et. al. [CaYaKiPeSh13]. Given the coordinate maps
is a square matrix and consequently the required terms are the entries of the inverse of the Jacobian. However, in general this is not the case, so we therefore implement the construction of these terms following the derivation in Cantwell, et. al. [CaYaKiPeSh13]. Given the coordinate maps 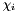 , this comprises of five steps
, this comprises of five steps
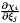 .
.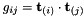 .
.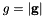 .
.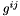 .
.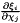 .
. Definition at line 80 of file GeomFactors.h.
| Nektar::SpatialDomains::GeomFactors::GeomFactors | ( | const GeomType | gtype, |
| const int | coordim, | ||
| const StdRegions::StdExpansionSharedPtr & | xmap, | ||
| const Array< OneD, Array< OneD, NekDouble > > & | coords | ||
| ) |
Constructor for GeomFactors class.
| gtype | Specified whether the geometry is regular or deformed. |
| coordim | Specifies the dimension of the coordinate system. |
| Coords | Coordinate maps of the element. |
Definition at line 89 of file GeomFactors.cpp.
References CheckIfValid().
| Nektar::SpatialDomains::GeomFactors::GeomFactors | ( | const GeomFactors & | S | ) |
Copy constructor.
| S | An instance of a GeomFactors class from which to construct a new instance. |
Definition at line 109 of file GeomFactors.cpp.
| Nektar::SpatialDomains::GeomFactors::~GeomFactors | ( | ) |
|
private |
Compute the transpose of the cofactors matrix.
Input and output arrays are of dimension (m_expDim*m_expDim) x num_points. The first index of the input and output arrays are ordered row-by-row.
| src | Input data array. |
| tgt | Storage for adjoint matrix data. |
Definition at line 589 of file GeomFactors.cpp.
References ASSERTL1, Vmath::Fill(), m_expDim, Vmath::Smul(), Vmath::Vcopy(), and Vmath::Vvtvvtm().
Referenced by ComputeDerivFactors(), ComputeGmat(), and ComputeJac().
|
private |
Tests if the element is valid and not self-intersecting.
Constructs the Jacobian as per Spencer's book p158 and tests if negative.
Definition at line 481 of file GeomFactors.cpp.
References Nektar::SpatialDomains::eMovingRegular, Nektar::SpatialDomains::eRegular, GetDeriv(), m_coordDim, m_expDim, m_type, m_valid, m_xmap, Vmath::Vmin(), Vmath::Vvtvp(), and Vmath::Vvtvvtm().
Referenced by GeomFactors().
|
private |
Derivatives are computed at the geometry point distributions and interpolated to the target point distributions.
| tpoints | Target point distributions. |
Definition at line 170 of file GeomFactors.cpp.
References ASSERTL1, Interp(), m_coordDim, m_coords, m_expDim, m_xmap, and Nektar::Utilities::same().
Referenced by ComputeDerivFactors(), ComputeGmat(), ComputeJac(), and GetDeriv().
|
private |
Return the derivative of the reference coordinates with respect to the mapping, 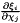 .
.
| keyTgt | Target point distributions. |
Definition at line 398 of file GeomFactors.cpp.
References Adjoint(), ASSERTL1, ComputeDeriv(), Nektar::SpatialDomains::eDeformed, m_coordDim, m_expDim, m_type, Vmath::Vdiv(), Vmath::Vsqrt(), and Vmath::Vvtvp().
Referenced by GetDerivFactors().
|
private |
Computes the Laplacian coefficients 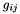 .
.
This routine returns a two-dimensional array of values specifying the inverse metric terms associated with the coordinate mapping of the corresponding reference region to the physical element. These terms correspond to the 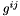 terms in [CaYaKiPeSh13] and, in the case of an embedded manifold, map covariant quantities to contravariant quantities. The leading index of the array is the index of the term in the tensor numbered as
terms in [CaYaKiPeSh13] and, in the case of an embedded manifold, map covariant quantities to contravariant quantities. The leading index of the array is the index of the term in the tensor numbered as
![\[\left(\begin{array}{ccc} 0 & 1 & 2 \\ 1 & 3 & 4 \\ 2 & 4 & 5 \end{array}\right)\]](form_208.png)
. The second dimension is either of size 1 in the case of elements having GeomType eRegular, or of size equal to the number of quadrature points for eDeformed elements.
Definition at line 333 of file GeomFactors.cpp.
References Adjoint(), ASSERTL1, ComputeDeriv(), Nektar::SpatialDomains::eDeformed, m_coordDim, m_expDim, m_type, Vmath::Vdiv(), and Vmath::Vvtvp().
Referenced by GetGmat().
|
private |
Return the Jacobian of the mapping and cache the result.
This routine returns an array of values specifying the Jacobian of the mapping at quadrature points in the element. The array is either of size 1 in the case of elements having GeomType eRegular, or of size equal to the number of quadrature points for eDeformed elements.
Definition at line 253 of file GeomFactors.cpp.
References Adjoint(), ASSERTL1, ComputeDeriv(), Nektar::SpatialDomains::eDeformed, m_coordDim, m_expDim, m_type, Vmath::Vsqrt(), and Vmath::Vvtvp().
Referenced by GetJac(), and Nektar::SpatialDomains::operator==().
|
inline |
Return the number of dimensions of the coordinate system.
This is greater than or equal to the expansion dimension.
Definition at line 297 of file GeomFactors.h.
References m_coordDim.
|
inline |
Return the derivative of the mapping with respect to the reference coordinates, 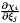 .
.
| tpoints | Target point distributions. |
Definition at line 207 of file GeomFactors.h.
References ComputeDeriv().
Referenced by CheckIfValid().
|
inline |
Return the derivative of the reference coordinates with respect to the mapping, 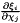 .
.
Returns cached value if available, otherwise computes derivative factors and stores result in cache.
| keyTgt | Target point distributions. |
Definition at line 262 of file GeomFactors.h.
References ComputeDerivFactors(), and m_derivFactorCache.
|
inline |
Return the Laplacian coefficients 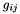 .
.
| keyTgt | Target point distributions. |
Definition at line 246 of file GeomFactors.h.
References ComputeGmat().
|
inline |
Returns whether the geometry is regular or deformed.
A geometric shape is considered regular if it has constant geometric information, and deformed if this information changes throughout the shape.
Definition at line 287 of file GeomFactors.h.
References m_type.
|
inline |
Computes a hash of this GeomFactors element.
The hash is computed from the geometry type, expansion dimension, coordinate dimension and Jacobian.
Definition at line 317 of file GeomFactors.h.
References Nektar::SpatialDomains::eDeformed, GetJac(), m_coordDim, m_expDim, m_type, and m_xmap.
|
inline |
Return the Jacobian of the mapping and cache the result.
Returns cached value if available, otherwise computes Jacobian and stores result in cache.
| keyTgt | Target point distributions. |
Definition at line 223 of file GeomFactors.h.
References ComputeJac(), and m_jacCache.
Referenced by GetHash().
|
inlineprotected |
Return the Xmap;.
Definition at line 337 of file GeomFactors.h.
References m_xmap.
|
private |
Perform interpolation of data between two point distributions.
| map_points | Source data point distribution. |
| src | Source data to be interpolated. |
| tpoints | Target data point distribution. |
| tgt | Target data storage. |
Definition at line 552 of file GeomFactors.cpp.
References ASSERTL1, Nektar::LibUtilities::Interp1D(), Nektar::LibUtilities::Interp2D(), Nektar::LibUtilities::Interp3D(), and m_expDim.
Referenced by ComputeDeriv().
|
inline |
Determine if element is valid and not self-intersecting.
The validity test is performed by testing if the Jacobian is negative at any point in the shape.
Definition at line 307 of file GeomFactors.h.
References m_valid.
|
friend |
Tests if two GeomFactors classes are equal.
Member data equivalence is tested in the following order: shape type, expansion dimension, coordinate dimension and coordinates.
Definition at line 132 of file GeomFactors.cpp.
|
protected |
Dimension of coordinate system.
Definition at line 137 of file GeomFactors.h.
Referenced by CheckIfValid(), ComputeDeriv(), ComputeDerivFactors(), ComputeGmat(), ComputeJac(), GetCoordim(), GetHash(), and Nektar::SpatialDomains::operator==().
Stores coordinates of the geometry.
Definition at line 143 of file GeomFactors.h.
Referenced by ComputeDeriv().
|
protected |
DerivFactors vector cache.
Definition at line 149 of file GeomFactors.h.
Referenced by GetDerivFactors().
|
protected |
Dimension of expansion.
Definition at line 135 of file GeomFactors.h.
Referenced by Adjoint(), CheckIfValid(), ComputeDeriv(), ComputeDerivFactors(), ComputeGmat(), ComputeJac(), GetHash(), Interp(), and Nektar::SpatialDomains::operator==().
|
protected |
|
protected |
Type of geometry (e.g. eRegular, eDeformed, eMovingRegular).
Definition at line 133 of file GeomFactors.h.
Referenced by CheckIfValid(), ComputeDerivFactors(), ComputeGmat(), ComputeJac(), GetGtype(), GetHash(), and Nektar::SpatialDomains::operator==().
|
protected |
Validity of element (Jacobian positive)
Definition at line 139 of file GeomFactors.h.
Referenced by CheckIfValid(), and IsValid().
|
protected |
Stores information about the expansion.
Definition at line 141 of file GeomFactors.h.
Referenced by CheckIfValid(), ComputeDeriv(), GetHash(), GetXmap(), and Nektar::SpatialDomains::operator==().
 1.8.9.1
1.8.9.1