|
Nektar++
|
|
Nektar++
|
Represents a basis of a given type. More...
#include <Basis.h>

Public Member Functions | |
| virtual | ~Basis () |
| Destructor. More... | |
| int | GetNumModes () const |
| Return order of basis from the basis specification. More... | |
| int | GetTotNumModes () const |
| Return total number of modes from the basis specification. More... | |
| int | GetNumPoints () const |
| Return the number of points from the basis specification. More... | |
| int | GetTotNumPoints () const |
| Return total number of points from the basis specification. More... | |
| BasisType | GetBasisType () const |
| Return the type of expansion basis. More... | |
| PointsKey | GetPointsKey () const |
| Return the points specification for the basis. More... | |
| PointsType | GetPointsType () const |
| Return the type of quadrature. More... | |
| const Array< OneD, const NekDouble > & | GetZ () const |
| const Array< OneD, const NekDouble > & | GetW () const |
| void | GetZW (Array< OneD, const NekDouble > &z, Array< OneD, const NekDouble > &w) const |
| const boost::shared_ptr < NekMatrix< NekDouble > > & | GetD (Direction dir=xDir) const |
| const boost::shared_ptr < NekMatrix< NekDouble > > | GetI (const Array< OneD, const NekDouble > &x) |
| const boost::shared_ptr < NekMatrix< NekDouble > > | GetI (const BasisKey &bkey) |
| bool | ExactIprodInt () const |
| Determine if basis has exact integration for inner product. More... | |
| bool | Collocation () const |
| Determine if basis has collocation properties. More... | |
| const Array< OneD, const NekDouble > & | GetBdata () const |
| Return basis definition array m_bdata. More... | |
| const Array< OneD, const NekDouble > & | GetDbdata () const |
| Return basis definition array m_dbdata. More... | |
| const BasisKey | GetBasisKey () const |
| Returns the specification for the Basis. More... | |
| virtual void | Initialize () |
Static Public Member Functions | |
| static boost::shared_ptr< Basis > | Create (const BasisKey &bkey) |
| Returns a new instance of a Basis with given BasisKey. More... | |
Protected Attributes | |
| BasisKey | m_basisKey |
| Basis specification. More... | |
| PointsSharedPtr | m_points |
| Set of points. More... | |
| Array< OneD, NekDouble > | m_bdata |
| Basis definition. More... | |
| Array< OneD, NekDouble > | m_dbdata |
| Derivative Basis definition. More... | |
| NekManager< BasisKey, NekMatrix< NekDouble > , BasisKey::opLess > | m_InterpManager |
Private Member Functions | |
| Basis (const BasisKey &bkey) | |
| Private constructor with BasisKey. More... | |
| Basis () | |
| Private default constructor. More... | |
| boost::shared_ptr< NekMatrix < NekDouble > > | CalculateInterpMatrix (const BasisKey &tbasis0) |
| Calculate the interpolation Matrix for coefficient from one base (m_basisKey) to another (tbasis0) More... | |
| void | GenBasis () |
| Generate appropriate basis and their derivatives. More... | |
|
inlinevirtual |
|
private |
Private constructor with BasisKey.
Definition at line 93 of file Basis.cpp.
References CalculateInterpMatrix(), and m_InterpManager.
|
inlineprivate |
Private default constructor.
Definition at line 340 of file Basis.h.
References ErrorUtil::efatal, and NEKERROR.
Referenced by Create().
|
private |
Calculate the interpolation Matrix for coefficient from one base (m_basisKey) to another (tbasis0)
Definition at line 122 of file Basis.cpp.
References Nektar::LibUtilities::BasisManager(), Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::BasisKey::GetBasisType(), Nektar::LibUtilities::BasisKey::GetNumModes(), and m_basisKey.
Referenced by Basis().
|
inline |
Determine if basis has collocation properties.
Definition at line 302 of file Basis.h.
References Nektar::LibUtilities::BasisKey::Collocation(), and m_basisKey.
|
inline |
Determine if basis has exact integration for inner product.
Definition at line 296 of file Basis.h.
References Nektar::LibUtilities::BasisKey::ExactIprodInt(), and m_basisKey.
|
private |
Generate appropriate basis and their derivatives.
The following expansions are generated depending on the enum type defined in m_basisKey.m_basistype:
NOTE: This definition does not follow the order in the Karniadakis & Sherwin book since this leads to a more compact hierarchical pattern for implementation purposes. The order of these modes dictates the ordering of the expansion coefficients.
In the following m_numModes = P
eModified_A:
m_bdata[i + j*m_numpoints] = 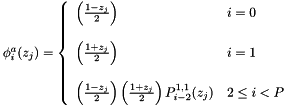
eModified_B:
m_bdata[n(i,j) + k*m_numpoints] = 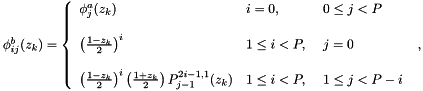
where 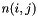 is a consecutive ordering of the triangular indices
is a consecutive ordering of the triangular indices 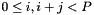 where j runs fastest.
where j runs fastest.
eModified_C:
m_bdata[n(i,j,k) + l*m_numpoints] = 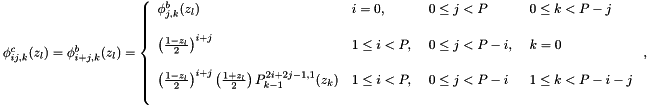
where 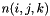 is a consecutive ordering of the triangular indices
is a consecutive ordering of the triangular indices 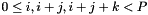 where k runs fastest, then j and finally i.
where k runs fastest, then j and finally i.
Orthogonal basis A
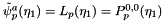
Orthogonal basis B
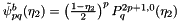 \
\
Orthogonal basis C
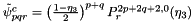 \
\
Definition at line 215 of file Basis.cpp.
References ASSERTL0, Nektar::LibUtilities::BasisManager(), Nektar::LibUtilities::eChebyshev, Nektar::LibUtilities::eFourier, Nektar::LibUtilities::eFourierHalfModeIm, Nektar::LibUtilities::eFourierHalfModeRe, Nektar::LibUtilities::eFourierSingleMode, Nektar::LibUtilities::eGauss_Lagrange, Nektar::LibUtilities::eGaussGaussLegendre, Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::eGLL_Lagrange, Nektar::LibUtilities::eLegendre, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::LibUtilities::eModified_C, Nektar::LibUtilities::eMonomial, Nektar::LibUtilities::eOrtho_A, Nektar::LibUtilities::eOrtho_B, Nektar::LibUtilities::eOrtho_C, GetBasisType(), Nektar::LibUtilities::BasisKey::GetNumModes(), GetNumModes(), GetNumPoints(), Nektar::LibUtilities::BasisKey::GetPointsKey(), Polylib::hgj(), Polylib::hglj(), Polylib::jacobfd(), m_basisKey, m_bdata, m_dbdata, m_points, Nektar::LibUtilities::PointsManager(), and Vmath::Vcopy().
Referenced by Initialize().
|
inline |
Returns the specification for the Basis.
Definition at line 320 of file Basis.h.
References m_basisKey.
|
inline |
Return the type of expansion basis.
Definition at line 242 of file Basis.h.
References Nektar::LibUtilities::BasisKey::GetBasisType(), and m_basisKey.
Referenced by GenBasis().
Return basis definition array m_bdata.
Definition at line 308 of file Basis.h.
References m_bdata.
|
inline |
Return basis definition array m_dbdata.
Definition at line 314 of file Basis.h.
References m_dbdata.
|
inline |
|
inline |
Definition at line 287 of file Basis.h.
References ASSERTL0, Nektar::LibUtilities::PointsKey::GetPointsDim(), Nektar::LibUtilities::BasisKey::GetPointsKey(), and m_InterpManager.
|
inline |
Return order of basis from the basis specification.
Definition at line 218 of file Basis.h.
References Nektar::LibUtilities::BasisKey::GetNumModes(), and m_basisKey.
Referenced by GenBasis(), and Initialize().
|
inline |
Return the number of points from the basis specification.
Definition at line 230 of file Basis.h.
References Nektar::LibUtilities::BasisKey::GetNumPoints(), and m_basisKey.
Referenced by GenBasis().
|
inline |
Return the points specification for the basis.
Definition at line 248 of file Basis.h.
References Nektar::LibUtilities::BasisKey::GetPointsKey(), and m_basisKey.
|
inline |
Return the type of quadrature.
Definition at line 254 of file Basis.h.
References Nektar::LibUtilities::BasisKey::GetPointsType(), and m_basisKey.
|
inline |
Return total number of modes from the basis specification.
Definition at line 224 of file Basis.h.
References Nektar::LibUtilities::BasisKey::GetTotNumModes(), and m_basisKey.
|
inline |
Return total number of points from the basis specification.
Definition at line 236 of file Basis.h.
References Nektar::LibUtilities::BasisKey::GetTotNumPoints(), and m_basisKey.
Referenced by Initialize().
|
inline |
|
virtual |
Definition at line 110 of file Basis.cpp.
References ASSERTL0, GenBasis(), GetNumModes(), and GetTotNumPoints().
|
protected |
Basis specification.
Definition at line 328 of file Basis.h.
Referenced by CalculateInterpMatrix(), Collocation(), ExactIprodInt(), GenBasis(), GetBasisKey(), GetBasisType(), GetNumModes(), GetNumPoints(), GetPointsKey(), GetPointsType(), GetTotNumModes(), and GetTotNumPoints().
Derivative Basis definition.
Definition at line 331 of file Basis.h.
Referenced by GenBasis(), and GetDbdata().
|
protected |
|
protected |
 1.8.8
1.8.8