Nektar++
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
Public Member Functions | Protected Member Functions | Private Member Functions | Private Attributes | List of all members
Nektar::LocalRegions::QuadExp Class Reference

#include <QuadExp.h>

Inheritance diagram for Nektar::LocalRegions::QuadExp:
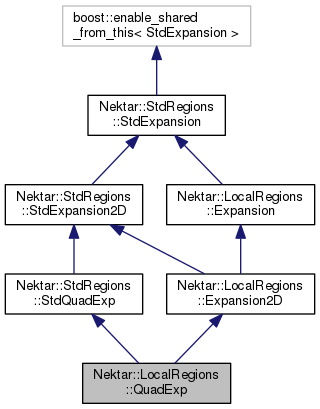
Inheritance graph
[legend]
Collaboration diagram for Nektar::LocalRegions::QuadExp:
Collaboration graph
[legend]

Public Member Functions

 QuadExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const SpatialDomains::QuadGeomSharedPtr &geom)
 Constructor using BasisKey class for quadrature points and order definition. More...
 
 QuadExp (const QuadExp &T)
 
virtual ~QuadExp ()
 
- Public Member Functions inherited from Nektar::StdRegions::StdQuadExp
 StdQuadExp ()
 
 StdQuadExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb)
 Constructor using BasisKey class for quadrature points and order definition. More...
 
 StdQuadExp (const StdQuadExp &T)
 Copy Constructor. More...
 
 ~StdQuadExp ()
 Destructor. More...
 
- Public Member Functions inherited from Nektar::StdRegions::StdExpansion2D
 StdExpansion2D ()
 
 StdExpansion2D (int numcoeffs, const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb)
 
 StdExpansion2D (const StdExpansion2D &T)
 
virtual ~StdExpansion2D ()
 
void PhysTensorDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray_d0, Array< OneD, NekDouble > &outarray_d1)
 Calculate the 2D derivative in the local tensor/collapsed coordinate at the physical points. More...
 
NekDouble Integral (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &w0, const Array< OneD, const NekDouble > &w1)
 
void BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0=true, bool doCheckCollDir1=true)
 
void IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0=true, bool doCheckCollDir1=true)
 
- Public Member Functions inherited from Nektar::StdRegions::StdExpansion
 StdExpansion ()
 Default Constructor. More...
 
 StdExpansion (const int numcoeffs, const int numbases, const LibUtilities::BasisKey &Ba=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bb=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bc=LibUtilities::NullBasisKey)
 Constructor. More...
 
 StdExpansion (const StdExpansion &T)
 Copy Constructor. More...
 
virtual ~StdExpansion ()
 Destructor. More...
 
int GetNumBases () const
 This function returns the number of 1D bases used in the expansion. More...
 
const Array< OneD, const
LibUtilities::BasisSharedPtr > & 		GetBase () const
 This function gets the shared point to basis. More...
 
const
LibUtilities::BasisSharedPtr & 		GetBasis (int dir) const
 This function gets the shared point to basis in the dir direction. More...
 
int GetNcoeffs (void) const
 This function returns the total number of coefficients used in the expansion. More...
 
int GetTotPoints () const
 This function returns the total number of quadrature points used in the element. More...
 
LibUtilities::BasisType GetBasisType (const int dir) const
 This function returns the type of basis used in the dir direction. More...
 
int GetBasisNumModes (const int dir) const
 This function returns the number of expansion modes in the dir direction. More...
 
int EvalBasisNumModesMax (void) const
 This function returns the maximum number of expansion modes over all local directions. More...
 
LibUtilities::PointsType GetPointsType (const int dir) const
 This function returns the type of quadrature points used in the dir direction. More...
 
int GetNumPoints (const int dir) const
 This function returns the number of quadrature points in the dir direction. More...
 
const Array< OneD, const
NekDouble > & 		GetPoints (const int dir) const
 This function returns a pointer to the array containing the quadrature points in dir direction. More...
 
int GetNverts () const
 This function returns the number of vertices of the expansion domain. More...
 
int GetNedges () const
 This function returns the number of edges of the expansion domain. More...
 
int GetEdgeNcoeffs (const int i) const
 This function returns the number of expansion coefficients belonging to the i-th edge. More...
 
int GetTotalEdgeIntNcoeffs () const
 
int GetEdgeNumPoints (const int i) const
 This function returns the number of quadrature points belonging to the i-th edge. More...
 
int DetCartesianDirOfEdge (const int edge)
 
const LibUtilities::BasisKey DetEdgeBasisKey (const int i) const
 
const LibUtilities::BasisKey DetFaceBasisKey (const int i, const int k) const
 
int GetFaceNumPoints (const int i) const
 This function returns the number of quadrature points belonging to the i-th face. More...
 
int GetFaceNcoeffs (const int i) const
 This function returns the number of expansion coefficients belonging to the i-th face. More...
 
int GetFaceIntNcoeffs (const int i) const
 
int GetTotalFaceIntNcoeffs () const
 
int GetTraceNcoeffs (const int i) const
 This function returns the number of expansion coefficients belonging to the i-th edge/face. More...
 
LibUtilities::PointsKey GetFacePointsKey (const int i, const int j) const
 
int NumBndryCoeffs (void) const
 
int NumDGBndryCoeffs (void) const
 
LibUtilities::BasisType GetEdgeBasisType (const int i) const
 This function returns the type of expansion basis on the i-th edge. More...
 
const LibUtilities::PointsKey GetNodalPointsKey () const
 This function returns the type of expansion Nodal point type if defined. More...
 
int GetNfaces () const
 This function returns the number of faces of the expansion domain. More...
 
int GetNtrace () const
 Returns the number of trace elements connected to this element. More...
 
LibUtilities::ShapeType DetShapeType () const
 This function returns the shape of the expansion domain. More...
 
boost::shared_ptr< StdExpansion > GetStdExp (void) const
 
int GetShapeDimension () const
 
bool IsBoundaryInteriorExpansion ()
 
bool IsNodalNonTensorialExp ()
 
void BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 This function performs the Backward transformation from coefficient space to physical space. More...
 
void FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 This function performs the Forward transformation from physical space to coefficient space. More...
 
void FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
NekDouble Integral (const Array< OneD, const NekDouble > &inarray)
 This function integrates the specified function over the domain. More...
 
void FillMode (const int mode, Array< OneD, NekDouble > &outarray)
 This function fills the array outarray with the mode-th mode of the expansion. More...
 
void IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 this function calculates the inner product of a given function f with the different modes of the expansion More...
 
void IProductWRTBase (const Array< OneD, const NekDouble > &base, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, int coll_check)
 
void IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
int GetElmtId ()
 Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...
 
void SetElmtId (const int id)
 Set the element id of this expansion when used in a list by returning value of m_elmt_id. More...
 
void GetCoords (Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2=NullNekDouble1DArray, Array< OneD, NekDouble > &coords_3=NullNekDouble1DArray)
 this function returns the physical coordinates of the quadrature points of the expansion More...
 
void GetCoord (const Array< OneD, const NekDouble > &Lcoord, Array< OneD, NekDouble > &coord)
 given the coordinates of a point of the element in the local collapsed coordinate system, this function calculates the physical coordinates of the point More...
 
DNekMatSharedPtr GetStdMatrix (const StdMatrixKey &mkey)
 
DNekBlkMatSharedPtr GetStdStaticCondMatrix (const StdMatrixKey &mkey)
 
IndexMapValuesSharedPtr GetIndexMap (const IndexMapKey &ikey)
 
const Array< OneD, const
NekDouble > & 		GetPhysNormals (void)
 
void SetPhysNormals (Array< OneD, const NekDouble > &normal)
 
virtual void SetUpPhysNormals (const int edge)
 
void NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, Array< OneD, NekDouble > &outarray)
 
void NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
void NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)
 
void NormVectorIProductWRTBase (const Array< OneD, const Array< OneD, NekDouble > > &Fvec, Array< OneD, NekDouble > &outarray)
 
DNekScalBlkMatSharedPtr GetLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)
 
void DropLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)
 
StdRegions::Orientation GetForient (int face)
 
StdRegions::Orientation GetEorient (int edge)
 
StdRegions::Orientation GetPorient (int point)
 
StdRegions::Orientation GetCartesianEorient (int edge)
 
void SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)
 
void SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
int CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)
 
void ExtractDataToCoeffs (const NekDouble *data, const std::vector< unsigned int > &nummodes, const int nmodes_offset, NekDouble *coeffs)
 
NekDouble StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)
 
int GetCoordim ()
 
void GetBoundaryMap (Array< OneD, unsigned int > &outarray)
 
void GetInteriorMap (Array< OneD, unsigned int > &outarray)
 
int GetVertexMap (const int localVertexId, bool useCoeffPacking=false)
 
void GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
void GetFaceInteriorMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
void GetEdgeToElementMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int P=-1)
 
void GetFaceToElementMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int nummodesA=-1, int nummodesB=-1)
 
void GetEdgePhysVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Extract the physical values along edge edge from inarray into outarray following the local edge orientation and point distribution defined by defined in EdgeExp. More...
 
void GetEdgePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GetTracePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GetVertexPhysVals (const int vertex, const Array< OneD, const NekDouble > &inarray, NekDouble &outarray)
 
void GetEdgeInterpVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GetEdgeQFactors (const int edge, Array< OneD, NekDouble > &outarray)
 Extract the metric factors to compute the contravariant fluxes along edge edge and stores them into outarray following the local edge orientation (i.e. anticlockwise convention). More...
 
void GetFacePhysVals (const int face, const boost::shared_ptr< StdExpansion > &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient=eNoOrientation)
 
void GetEdgePhysMap (const int edge, Array< OneD, int > &outarray)
 
void GetFacePhysMap (const int face, Array< OneD, int > &outarray)
 
void MultiplyByQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
DNekMatSharedPtr CreateGeneralMatrix (const StdMatrixKey &mkey)
 this function generates the mass matrix $\mathbf{M}[i][j] = \int \phi_i(\mathbf{x}) \phi_j(\mathbf{x}) d\mathbf{x}$ More...
 
void GeneralMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDerivMatrixOp (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDirectionalDerivMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassLevelCurvatureMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LinearAdvectionDiffusionReactionMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)
 
void HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
DNekMatSharedPtr GenMatrix (const StdMatrixKey &mkey)
 
void PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
 
void PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void PhysDeriv_s (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_ds)
 
void PhysDeriv_n (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_dn)
 
void PhysDirectionalDeriv (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &direction, Array< OneD, NekDouble > &outarray)
 
void StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
 
void StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void AddRobinMassMatrix (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, DNekMatSharedPtr &inoutmat)
 
void AddRobinEdgeContribution (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, Array< OneD, NekDouble > &coeffs)
 
NekDouble PhysEvaluate (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
 This function evaluates the expansion at a single (arbitrary) point of the domain. More...
 
NekDouble PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)
 This function evaluates the expansion at a single (arbitrary) point of the domain. More...
 
void LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)
 Convert local cartesian coordinate xi into local collapsed coordinates eta. More...
 
const boost::shared_ptr
< SpatialDomains::GeomFactors > & 		GetMetricInfo (void) const
 
virtual int v_GetElmtId ()
 Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...
 
virtual const Array< OneD,
const NekDouble > & 		v_GetPhysNormals (void)
 
virtual void v_SetPhysNormals (Array< OneD, const NekDouble > &normal)
 
virtual void v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, Array< OneD, NekDouble > &outarray)
 
virtual void v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
virtual StdRegions::Orientation v_GetForient (int face)
 
virtual StdRegions::Orientation v_GetPorient (int point)
 
NekDouble Linf (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
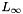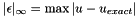 Function to evaluate the discrete $ L_\infty$ error $ |\epsilon|_\infty = \max |u - u_{exact}|$ where $ u_{exact}$ is given by the array sol. More...
 
NekDouble L2 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
 Function to evaluate the discrete 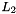$ L_2$ error, $ | \epsilon |_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 dx \right]^{1/2} d\xi_1 $ where $ u_{exact}$ is given by the array sol. More...
 
NekDouble H1 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
 Function to evaluate the discrete 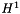$ H^1$ error, $ | \epsilon |^1_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 + \nabla(u - u_{exact})\cdot\nabla(u - u_{exact})\cdot dx \right]^{1/2} d\xi_1 $ where $ u_{exact}$ is given by the array sol. More...
 
const NormalVector & GetEdgeNormal (const int edge) const
 
void ComputeEdgeNormal (const int edge)
 
void NegateEdgeNormal (const int edge)
 
bool EdgeNormalNegated (const int edge)
 
void ComputeFaceNormal (const int face)
 
void NegateFaceNormal (const int face)
 
bool FaceNormalNegated (const int face)
 
void ComputeVertexNormal (const int vertex)
 
const NormalVector & GetFaceNormal (const int face) const
 
const NormalVector & GetVertexNormal (const int vertex) const
 
const NormalVector & GetSurfaceNormal (const int id) const
 
const LibUtilities::PointsKeyVector GetPointsKeys () const
 
Array< OneD, unsigned int > GetEdgeInverseBoundaryMap (int eid)
 
Array< OneD, unsigned int > GetFaceInverseBoundaryMap (int fid, StdRegions::Orientation faceOrient=eNoOrientation)
 
DNekMatSharedPtr BuildInverseTransformationMatrix (const DNekScalMatSharedPtr &m_transformationmatrix)
 
void PhysInterpToSimplexEquiSpaced (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, int npset=-1)
 This function performs an interpolation from the physical space points provided at input into an array of equispaced points which are not the collapsed coordinate. So for a tetrahedron you will only get a tetrahedral number of values. More...
 
void GetSimplexEquiSpacedConnectivity (Array< OneD, int > &conn, bool standard=true)
 This function provides the connectivity of local simplices (triangles or tets) to connect the equispaced data points provided by PhysInterpToSimplexEquiSpaced. More...
 
void EquiSpacedToCoeffs (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 This function performs a projection/interpolation from the equispaced points sometimes used in post-processing onto the coefficient space. More...
 
template<class T >
boost::shared_ptr< T > as ()
 
void IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)
 
- Public Member Functions inherited from Nektar::LocalRegions::Expansion2D
 Expansion2D (SpatialDomains::Geometry2DSharedPtr pGeom)
 
virtual ~Expansion2D ()
 
void SetTraceToGeomOrientation (Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, NekDouble > &inout)
 
Expansion1DSharedPtr GetEdgeExp (int edge, bool SetUpNormal=true)
 
void SetEdgeExp (const int edge, Expansion1DSharedPtr &e)
 
void AddNormTraceInt (const int dir, Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, Array< OneD, NekDouble > > &edgeCoeffs, Array< OneD, NekDouble > &outarray)
 
void AddNormTraceInt (const int dir, Array< OneD, const NekDouble > &inarray, Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, NekDouble > &outarray, const StdRegions::VarCoeffMap &varcoeffs)
 
void AddEdgeBoundaryInt (const int edge, ExpansionSharedPtr &EdgeExp, Array< OneD, NekDouble > &edgePhys, Array< OneD, NekDouble > &outarray, const StdRegions::VarCoeffMap &varcoeffs=StdRegions::NullVarCoeffMap)
 
void AddHDGHelmholtzEdgeTerms (const NekDouble tau, const int edge, Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, NekDouble > &edgePhys, const StdRegions::VarCoeffMap &dirForcing, Array< OneD, NekDouble > &outarray)
 
void AddHDGHelmholtzTraceTerms (const NekDouble tau, const Array< OneD, const NekDouble > &inarray, Array< OneD, ExpansionSharedPtr > &EdgeExp, const StdRegions::VarCoeffMap &dirForcing, Array< OneD, NekDouble > &outarray)
 
Expansion3DSharedPtr GetLeftAdjacentElementExp () const
 
Expansion3DSharedPtr GetRightAdjacentElementExp () const
 
int GetLeftAdjacentElementFace () const
 
int GetRightAdjacentElementFace () const
 
void SetAdjacentElementExp (int face, Expansion3DSharedPtr &f)
 
SpatialDomains::Geometry2DSharedPtr GetGeom2D () const
 
void ReOrientEdgePhysMap (const int nvert, const StdRegions::Orientation orient, const int nq0, Array< OneD, int > &idmap)
 
- Public Member Functions inherited from Nektar::LocalRegions::Expansion
 Expansion (SpatialDomains::GeometrySharedPtr pGeom)
 
 Expansion (const Expansion &pSrc)
 
virtual ~Expansion ()
 
DNekScalMatSharedPtr GetLocMatrix (const LocalRegions::MatrixKey &mkey)
 
DNekScalMatSharedPtr GetLocMatrix (const StdRegions::MatrixType mtype, const StdRegions::ConstFactorMap &factors=StdRegions::NullConstFactorMap, const StdRegions::VarCoeffMap &varcoeffs=StdRegions::NullVarCoeffMap)
 
SpatialDomains::GeometrySharedPtr GetGeom () const
 
void Reset ()
 
DNekMatSharedPtr BuildTransformationMatrix (const DNekScalMatSharedPtr &r_bnd, const StdRegions::MatrixType matrixType)
 
DNekMatSharedPtr BuildVertexMatrix (const DNekScalMatSharedPtr &r_bnd)
 
void AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
void AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
void AddFaceNormBoundaryInt (const int face, const boost::shared_ptr< Expansion > &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
void DGDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, Array< OneD, NekDouble > > &coeffs, Array< OneD, NekDouble > &outarray)
 

Protected Member Functions

virtual NekDouble v_Integral (const Array< OneD, const NekDouble > &inarray)
 Integrates the specified function over the domain. More...
 
virtual NekDouble v_StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)
 
virtual void v_PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
 Calculate the derivative of the physical points. More...
 
virtual void v_PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Calculate the derivative of the physical points in a given direction. More...
 
virtual void v_PhysDirectionalDeriv (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &direction, Array< OneD, NekDouble > &out)
 Physical derivative along a direction vector. More...
 
virtual void v_FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Transform a given function from physical quadrature space to coefficient space. More...
 
virtual void v_FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Calculate the inner product of inarray with respect to the basis B=base0*base1 and put into outarray. More...
 
virtual void v_IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)
 
virtual void v_IProductWRTBase_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_IProductWRTDerivBase_MatOp (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)
 
virtual void v_NormVectorIProductWRTBase (const Array< OneD, const Array< OneD, NekDouble > > &Fvec, Array< OneD, NekDouble > &outarray)
 
virtual
StdRegions::StdExpansionSharedPtr 		v_GetStdExp (void) const
 
virtual void v_GetCoord (const Array< OneD, const NekDouble > &Lcoords, Array< OneD, NekDouble > &coords)
 
virtual void v_GetCoords (Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2, Array< OneD, NekDouble > &coords_3)
 
virtual NekDouble v_PhysEvaluate (const Array< OneD, const NekDouble > &coord, const Array< OneD, const NekDouble > &physvals)
 This function evaluates the expansion at a single (arbitrary) point of the domain. More...
 
virtual void v_GetEdgePhysVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Extract the physical values along edge edge from inarray into outarray following the local edge orientation and point distribution defined by defined in EdgeExp. More...
 
virtual void v_GetEdgePhysVals (const int edge, const StdRegions::StdExpansionSharedPtr &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_GetTracePhysVals (const int edge, const StdRegions::StdExpansionSharedPtr &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient)
 
virtual void v_GetEdgeInterpVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_GetEdgeQFactors (const int edge, Array< OneD, NekDouble > &outarray)
 
virtual void v_ComputeEdgeNormal (const int edge)
 
virtual const
SpatialDomains::GeomFactorsSharedPtr & 		v_GetMetricInfo () const
 
virtual int v_GetCoordim ()
 
virtual void v_ExtractDataToCoeffs (const NekDouble *data, const std::vector< unsigned int > &nummodes, const int mode_offset, NekDouble *coeffs)
 Unpack data from input file assuming it comes from the same expansion type. More...
 
virtual StdRegions::Orientation v_GetEorient (int edge)
 
virtual StdRegions::Orientation v_GetCartesianEorient (int edge)
 
virtual const
LibUtilities::BasisSharedPtr & 		v_GetBasis (int dir) const
 
virtual int v_GetNumPoints (const int dir) const
 
virtual void v_GetEdgePhysMap (const int edge, Array< OneD, int > &outarray)
 
virtual DNekMatSharedPtr v_GenMatrix (const StdRegions::StdMatrixKey &mkey)
 
virtual DNekMatSharedPtr v_CreateStdMatrix (const StdRegions::StdMatrixKey &mkey)
 
DNekScalMatSharedPtr CreateMatrix (const MatrixKey &mkey)
 
DNekScalBlkMatSharedPtr CreateStaticCondMatrix (const MatrixKey &mkey)
 
virtual DNekScalMatSharedPtr v_GetLocMatrix (const MatrixKey &mkey)
 
virtual DNekScalBlkMatSharedPtr v_GetLocStaticCondMatrix (const MatrixKey &mkey)
 
void v_DropLocStaticCondMatrix (const MatrixKey &mkey)
 
virtual void v_MassMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_WeakDerivMatrixOp (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_WeakDirectionalDerivMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_MassLevelCurvatureMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_GeneralMatrixOp_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_LaplacianMatrixOp_MatFree_Kernel (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp)
 
virtual void v_ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_ComputeLaplacianMetric ()
 
virtual void v_SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdRegions::StdMatrixKey &mkey)
 
- Protected Member Functions inherited from Nektar::StdRegions::StdQuadExp
virtual void v_StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
 
virtual void v_StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1)
 
virtual void v_IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1)
 
virtual void v_LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)
 
virtual void v_FillMode (const int mode, Array< OneD, NekDouble > &array)
 Fill outarray with mode mode of expansion. More...
 
virtual int v_GetNverts () const
 
virtual int v_GetNedges () const
 
virtual int v_GetEdgeNcoeffs (const int i) const
 
virtual int v_GetEdgeNumPoints (const int i) const
 
virtual int v_NumBndryCoeffs () const
 
virtual int v_NumDGBndryCoeffs () const
 
virtual LibUtilities::BasisType v_GetEdgeBasisType (const int i) const
 
virtual int v_DetCartesianDirOfEdge (const int edge)
 
virtual int v_CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)
 
virtual const
LibUtilities::BasisKey 		v_DetEdgeBasisKey (const int i) const
 
virtual LibUtilities::ShapeType v_DetShapeType () const
 
virtual bool v_IsBoundaryInteriorExpansion ()
 
virtual void v_GetBoundaryMap (Array< OneD, unsigned int > &outarray)
 
virtual void v_GetInteriorMap (Array< OneD, unsigned int > &outarray)
 
virtual int v_GetVertexMap (int localVertexId, bool useCoeffPacking=false)
 
virtual void v_GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
void v_GetEdgeToElementMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int P=-1)
 
void v_GeneralMatrixOp_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void v_MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_GetSimplexEquiSpacedConnectivity (Array< OneD, int > &conn, bool standard=true)
 
- Protected Member Functions inherited from Nektar::StdRegions::StdExpansion2D
virtual NekDouble v_PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)
 
virtual void v_LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual int v_GetTraceNcoeffs (const int i) const
 
- Protected Member Functions inherited from Nektar::StdRegions::StdExpansion
DNekMatSharedPtr CreateStdMatrix (const StdMatrixKey &mkey)
 
DNekBlkMatSharedPtr CreateStdStaticCondMatrix (const StdMatrixKey &mkey)
 Create the static condensation of a matrix when using a boundary interior decomposition. More...
 
IndexMapValuesSharedPtr CreateIndexMap (const IndexMapKey &ikey)
 Create an IndexMap which contains mapping information linking any specific element shape with either its boundaries, edges, faces, verteces, etc. More...
 
void BwdTrans_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GeneralMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp_MatFree_Kernel (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp)
 
void LaplacianMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp_MatFree (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDerivMatrixOp_MatFree (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDirectionalDerivMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassLevelCurvatureMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LinearAdvectionDiffusionReactionMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)
 
void HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void HelmholtzMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
virtual void v_SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)
 
- Protected Member Functions inherited from Nektar::LocalRegions::Expansion2D
virtual void v_DGDeriv (const int dir, const Array< OneD, const NekDouble > &incoeffs, Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, Array< OneD, NekDouble > > &edgeCoeffs, Array< OneD, NekDouble > &out_d)
 
virtual void v_AddEdgeNormBoundaryInt (const int edge, const ExpansionSharedPtr &EdgeExp, const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddEdgeNormBoundaryInt (const int edge, const ExpansionSharedPtr &EdgeExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddRobinMassMatrix (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, DNekMatSharedPtr &inoutmat)
 
virtual void v_AddRobinEdgeContribution (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, Array< OneD, NekDouble > &coeffs)
 
virtual DNekMatSharedPtr v_BuildVertexMatrix (const DNekScalMatSharedPtr &r_bnd)
 
void GetPhysEdgeVarCoeffsFromElement (const int edge, ExpansionSharedPtr &EdgeExp, const Array< OneD, const NekDouble > &varcoeff, Array< OneD, NekDouble > &outarray)
 
void ReOrientQuadEdgePhysMap (const StdRegions::Orientation orient, const int nq0, Array< OneD, int > &idmap)
 
Array< OneD, unsigned int > v_GetEdgeInverseBoundaryMap (int eid)
 
virtual void v_NegateEdgeNormal (const int edge)
 
virtual bool v_EdgeNormalNegated (const int edge)
 
virtual void v_SetUpPhysNormals (const int edge)
 
const StdRegions::NormalVector & v_GetEdgeNormal (const int edge) const
 
const StdRegions::NormalVector & v_GetSurfaceNormal (const int id) const
 
- Protected Member Functions inherited from Nektar::LocalRegions::Expansion
void ComputeLaplacianMetric ()
 
void ComputeQuadratureMetric ()
 
virtual void v_MultiplyByQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual DNekMatSharedPtr v_BuildTransformationMatrix (const DNekScalMatSharedPtr &r_bnd, const StdRegions::MatrixType matrixType)
 
virtual void v_AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddFaceNormBoundaryInt (const int face, const boost::shared_ptr< Expansion > &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 

Private Member Functions

 QuadExp ()
 

Private Attributes

LibUtilities::NekManager
< MatrixKey, DNekScalMat,
MatrixKey::opLess > 		m_matrixManager
 
LibUtilities::NekManager
< MatrixKey, DNekScalBlkMat,
MatrixKey::opLess > 		m_staticCondMatrixManager
 

Additional Inherited Members

- Protected Attributes inherited from Nektar::StdRegions::StdExpansion
Array< OneD,
LibUtilities::BasisSharedPtr > 		m_base
 
int m_elmt_id
 
int m_ncoeffs
 
LibUtilities::NekManager
< StdMatrixKey, DNekMat,
StdMatrixKey::opLess > 		m_stdMatrixManager
 
LibUtilities::NekManager
< StdMatrixKey, DNekBlkMat,
StdMatrixKey::opLess > 		m_stdStaticCondMatrixManager
 
LibUtilities::NekManager
< IndexMapKey, IndexMapValues,
IndexMapKey::opLess > 		m_IndexMapManager
 
- Protected Attributes inherited from Nektar::LocalRegions::Expansion2D
std::vector< Expansion1DWeakPtr > m_edgeExp
 
std::vector< bool > m_requireNeg
 
std::map< int,
StdRegions::NormalVector > 		m_edgeNormals
 
std::map< int, bool > m_negatedNormals
 
Expansion3DWeakPtr m_elementLeft
 
Expansion3DWeakPtr m_elementRight
 
int m_elementFaceLeft
 
int m_elementFaceRight
 
- Protected Attributes inherited from Nektar::LocalRegions::Expansion
SpatialDomains::GeometrySharedPtr m_geom
 
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
 
MetricMap m_metrics
 

Detailed Description

Definition at line 52 of file QuadExp.h.

Constructor & Destructor Documentation

Nektar::LocalRegions::QuadExp::QuadExp ( const LibUtilities::BasisKey &  Ba,
const LibUtilities::BasisKey &  Bb,
const SpatialDomains::QuadGeomSharedPtr &  geom 
)

Constructor using BasisKey class for quadrature points and order definition.

Definition at line 49 of file QuadExp.cpp.

51  :
52  StdExpansion (Ba.GetNumModes()*Bb.GetNumModes(),2,Ba,Bb),
53  StdExpansion2D(Ba.GetNumModes()*Bb.GetNumModes(),Ba,Bb),
54  StdQuadExp (Ba,Bb),
55  Expansion (geom),
56  Expansion2D (geom),
57  m_matrixManager(
58  boost::bind(&QuadExp::CreateMatrix, this, _1),
59  std::string("QuadExpMatrix")),
60  m_staticCondMatrixManager(
61  boost::bind(&QuadExp::CreateStaticCondMatrix, this, _1),
62  std::string("QuadExpStaticCondMatrix"))
63  {
64  }
Nektar::LocalRegions::QuadExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: QuadExp.h:286
Nektar::LocalRegions::QuadExp::CreateStaticCondMatrix
DNekScalBlkMatSharedPtr CreateStaticCondMatrix(const MatrixKey &mkey)
Definition: QuadExp.cpp:1928
Nektar::LocalRegions::Expansion::Expansion
Expansion(SpatialDomains::GeometrySharedPtr pGeom)
Definition: Expansion.cpp:48
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
Nektar::LocalRegions::QuadExp::CreateMatrix
DNekScalMatSharedPtr CreateMatrix(const MatrixKey &mkey)
Definition: QuadExp.cpp:1614
Nektar::LocalRegions::Expansion2D::Expansion2D
Expansion2D(SpatialDomains::Geometry2DSharedPtr pGeom)
Definition: Expansion2D.cpp:49
Nektar::StdRegions::StdExpansion::StdExpansion
StdExpansion()
Default Constructor.
Definition: StdExpansion.cpp:44
Nektar::LocalRegions::QuadExp::QuadExp ( const QuadExp &  T)

Definition at line 67 of file QuadExp.cpp.

67  :
68  StdExpansion(T),
69  StdExpansion2D(T),
70  StdQuadExp(T),
71  Expansion (T),
72  Expansion2D (T),
73  m_matrixManager(T.m_matrixManager),
74  m_staticCondMatrixManager(T.m_staticCondMatrixManager)
75  {
76  }
Nektar::LocalRegions::QuadExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: QuadExp.h:286
Nektar::LocalRegions::Expansion::Expansion
Expansion(SpatialDomains::GeometrySharedPtr pGeom)
Definition: Expansion.cpp:48
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
Nektar::LocalRegions::Expansion2D::Expansion2D
Expansion2D(SpatialDomains::Geometry2DSharedPtr pGeom)
Definition: Expansion2D.cpp:49
Nektar::StdRegions::StdExpansion::StdExpansion
StdExpansion()
Default Constructor.
Definition: StdExpansion.cpp:44
Nektar::LocalRegions::QuadExp::~QuadExp ( )
virtual

Definition at line 79 of file QuadExp.cpp.

80  {
81  }
Nektar::LocalRegions::QuadExp::QuadExp ( )
private

Member Function Documentation

DNekScalMatSharedPtr Nektar::LocalRegions::QuadExp::CreateMatrix ( const MatrixKey &  mkey)
protected

Definition at line 1614 of file QuadExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), ASSERTL2, Nektar::LocalRegions::Expansion::BuildVertexMatrix(), Nektar::StdRegions::StdMatrixKey::ConstFactorExists(), Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::eFactorGaussEdge, Nektar::StdRegions::eFactorLambda, Nektar::StdRegions::eFactorSVVCutoffRatio, Nektar::StdRegions::eHelmholtz, Nektar::StdRegions::eHybridDGHelmholtz, Nektar::StdRegions::eInterpGauss, Nektar::StdRegions::eInvHybridDGHelmholtz, Nektar::StdRegions::eInvLaplacianWithUnityMean, Nektar::StdRegions::eInvMass, Nektar::StdRegions::eIProductWRTBase, Nektar::StdRegions::eIProductWRTDerivBase0, Nektar::StdRegions::eIProductWRTDerivBase1, Nektar::StdRegions::eIProductWRTDerivBase2, Nektar::StdRegions::eLaplacian, Nektar::StdRegions::eLaplacian00, Nektar::StdRegions::eLaplacian01, Nektar::StdRegions::eLaplacian11, Nektar::StdRegions::eMass, Nektar::SpatialDomains::eNoGeomType, Nektar::StdRegions::ePreconLinearSpace, Nektar::StdRegions::eWeakDeriv0, Nektar::StdRegions::eWeakDeriv1, Nektar::StdRegions::eWeakDeriv2, Nektar::StdRegions::StdExpansion::GenMatrix(), Nektar::StdRegions::StdMatrixKey::GetConstFactor(), Nektar::StdRegions::StdMatrixKey::GetConstFactors(), Nektar::StdRegions::StdExpansion::GetLocStaticCondMatrix(), Nektar::StdRegions::StdMatrixKey::GetMatrixType(), Nektar::StdRegions::StdMatrixKey::GetNVarCoeff(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdMatrixKey::GetShapeType(), Nektar::StdRegions::StdExpansion::GetStdMatrix(), Nektar::StdRegions::StdMatrixKey::GetVarCoeffs(), Nektar::StdRegions::StdExpansion::m_base, m_matrixManager, Nektar::LocalRegions::Expansion::m_metricinfo, and Nektar::Transpose().

1615  {
1616  DNekScalMatSharedPtr returnval;
1617  LibUtilities::PointsKeyVector ptsKeys = GetPointsKeys();
1618 
1619  ASSERTL2(m_metricinfo->GetGtype() != SpatialDomains::eNoGeomType,
1620  "Geometric information is not set up");
1621 
1622  switch (mkey.GetMatrixType())
1623  {
1624  case StdRegions::eMass:
1625  {
1626  if ((m_metricinfo->GetGtype() ==
1627  SpatialDomains::eDeformed) || (mkey.GetNVarCoeff()))
1628  {
1629  NekDouble one = 1.0;
1630  DNekMatSharedPtr mat = GenMatrix(mkey);
1631  returnval = MemoryManager<DNekScalMat>::
1632  AllocateSharedPtr(one,mat);
1633  }
1634  else
1635  {
1636  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1637  DNekMatSharedPtr mat = GetStdMatrix(mkey);
1638  returnval = MemoryManager<DNekScalMat>::
1639  AllocateSharedPtr(jac,mat);
1640  }
1641  }
1642  break;
1643  case StdRegions::eInvMass:
1644  {
1645  if ((m_metricinfo->GetGtype() ==
1646  SpatialDomains::eDeformed) || (mkey.GetNVarCoeff()))
1647  {
1648  NekDouble one = 1.0;
1649  StdRegions::StdMatrixKey masskey(
1650  StdRegions::eMass, DetShapeType(), *this);
1651  DNekMatSharedPtr mat = GenMatrix(masskey);
1652  mat->Invert();
1653 
1654  returnval = MemoryManager<DNekScalMat>::
1655  AllocateSharedPtr(one,mat);
1656  }
1657  else
1658  {
1659  NekDouble fac = 1.0/(m_metricinfo->GetJac(ptsKeys))[0];
1660  DNekMatSharedPtr mat = GetStdMatrix(mkey);
1661  returnval = MemoryManager<DNekScalMat>::
1662  AllocateSharedPtr(fac,mat);
1663  }
1664  }
1665  break;
1666  case StdRegions::eWeakDeriv0:
1667  case StdRegions::eWeakDeriv1:
1668  case StdRegions::eWeakDeriv2:
1669  {
1670  if((m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1671  || (mkey.GetNVarCoeff()))
1672  {
1673  NekDouble one = 1.0;
1674  DNekMatSharedPtr mat = GenMatrix(mkey);
1675 
1676  returnval = MemoryManager<DNekScalMat>::
1677  AllocateSharedPtr(one,mat);
1678  }
1679  else
1680  {
1681  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1682  Array<TwoD, const NekDouble> df =
1683  m_metricinfo->GetDerivFactors(ptsKeys);
1684  int dir = 0;
1685 
1686  switch(mkey.GetMatrixType())
1687  {
1688  case StdRegions::eWeakDeriv0:
1689  dir = 0;
1690  break;
1691  case StdRegions::eWeakDeriv1:
1692  dir = 1;
1693  break;
1694  case StdRegions::eWeakDeriv2:
1695  dir = 2;
1696  break;
1697  default:
1698  break;
1699  }
1700 
1701  MatrixKey deriv0key(StdRegions::eWeakDeriv0,
1702  mkey.GetShapeType(), *this);
1703  MatrixKey deriv1key(StdRegions::eWeakDeriv1,
1704  mkey.GetShapeType(), *this);
1705 
1706  DNekMat &deriv0 = *GetStdMatrix(deriv0key);
1707  DNekMat &deriv1 = *GetStdMatrix(deriv1key);
1708 
1709  int rows = deriv0.GetRows();
1710  int cols = deriv1.GetColumns();
1711 
1712  DNekMatSharedPtr WeakDeriv = MemoryManager<DNekMat>::
1713  AllocateSharedPtr(rows,cols);
1714  (*WeakDeriv) = df[2*dir][0]*deriv0 +
1715  df[2*dir+1][0]*deriv1;
1716  returnval = MemoryManager<DNekScalMat>::
1717  AllocateSharedPtr(jac,WeakDeriv);
1718  }
1719  }
1720  break;
1721  case StdRegions::eLaplacian:
1722  {
1723  if( (m_metricinfo->GetGtype() ==
1724  SpatialDomains::eDeformed) || (mkey.GetNVarCoeff() > 0)
1725  || (mkey.ConstFactorExists
1726  (StdRegions::eFactorSVVCutoffRatio)))
1727  {
1728  NekDouble one = 1.0;
1729  DNekMatSharedPtr mat = GenMatrix(mkey);
1730 
1731  returnval = MemoryManager<DNekScalMat>::
1732  AllocateSharedPtr(one,mat);
1733  }
1734  else
1735  {
1736  MatrixKey lap00key(StdRegions::eLaplacian00,
1737  mkey.GetShapeType(), *this);
1738  MatrixKey lap01key(StdRegions::eLaplacian01,
1739  mkey.GetShapeType(), *this);
1740  MatrixKey lap11key(StdRegions::eLaplacian11,
1741  mkey.GetShapeType(), *this);
1742 
1743  DNekMat &lap00 = *GetStdMatrix(lap00key);
1744  DNekMat &lap01 = *GetStdMatrix(lap01key);
1745  DNekMat &lap11 = *GetStdMatrix(lap11key);
1746 
1747  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1748  Array<TwoD, const NekDouble>
1749  gmat = m_metricinfo->GetGmat(ptsKeys);
1750 
1751  int rows = lap00.GetRows();
1752  int cols = lap00.GetColumns();
1753 
1754  DNekMatSharedPtr lap =
1755  MemoryManager<DNekMat>::AllocateSharedPtr(rows,cols);
1756 
1757  (*lap) = gmat[0][0] * lap00 +
1758  gmat[1][0] * (lap01 + Transpose(lap01)) +
1759  gmat[3][0] * lap11;
1760 
1761  returnval = MemoryManager<DNekScalMat>::
1762  AllocateSharedPtr(jac,lap);
1763  }
1764  }
1765  break;
1766  case StdRegions::eInvLaplacianWithUnityMean:
1767  {
1768  DNekMatSharedPtr mat = GenMatrix(mkey);
1769  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(1.0,mat);
1770  }
1771  break;
1772  case StdRegions::eHelmholtz:
1773  {
1774  NekDouble lambda =
1775  mkey.GetConstFactor(StdRegions::eFactorLambda);
1776 
1777  MatrixKey masskey(mkey, StdRegions::eMass);
1778  DNekScalMat &MassMat = *(this->m_matrixManager[masskey]);
1779 
1780  MatrixKey lapkey(mkey, StdRegions::eLaplacian);
1781  DNekScalMat &LapMat = *(this->m_matrixManager[lapkey]);
1782 
1783  int rows = LapMat.GetRows();
1784  int cols = LapMat.GetColumns();
1785 
1786  DNekMatSharedPtr helm = MemoryManager<DNekMat>::
1787  AllocateSharedPtr(rows,cols);
1788 
1789  NekDouble one = 1.0;
1790  (*helm) = LapMat + lambda*MassMat;
1791 
1792  returnval =
1793  MemoryManager<DNekScalMat>::AllocateSharedPtr(one,helm);
1794  }
1795  break;
1796  case StdRegions::eIProductWRTBase:
1797  {
1798  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1799  {
1800  NekDouble one = 1.0;
1801  DNekMatSharedPtr mat = GenMatrix(mkey);
1802  returnval = MemoryManager<DNekScalMat>::
1803  AllocateSharedPtr(one,mat);
1804  }
1805  else
1806  {
1807  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1808  DNekMatSharedPtr mat = GetStdMatrix(mkey);
1809  returnval = MemoryManager<DNekScalMat>::
1810  AllocateSharedPtr(jac,mat);
1811  }
1812  }
1813  break;
1814  case StdRegions::eIProductWRTDerivBase0:
1815  case StdRegions::eIProductWRTDerivBase1:
1816  case StdRegions::eIProductWRTDerivBase2:
1817  {
1818  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1819  {
1820  NekDouble one = 1.0;
1821  DNekMatSharedPtr mat = GenMatrix(mkey);
1822  returnval = MemoryManager<DNekScalMat>::
1823  AllocateSharedPtr(one,mat);
1824  }
1825  else
1826  {
1827  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1828  const Array<TwoD, const NekDouble>& df =
1829  m_metricinfo->GetDerivFactors(ptsKeys);
1830  int dir = 0;
1831 
1832  switch(mkey.GetMatrixType())
1833  {
1834  case StdRegions::eIProductWRTDerivBase0:
1835  dir = 0;
1836  break;
1837  case StdRegions::eIProductWRTDerivBase1:
1838  dir = 1;
1839  break;
1840  case StdRegions::eIProductWRTDerivBase2:
1841  dir = 2;
1842  break;
1843  default:
1844  break;
1845  }
1846 
1847  MatrixKey iProdDeriv0Key(
1848  StdRegions::eIProductWRTDerivBase0,
1849  mkey.GetShapeType(), *this);
1850  MatrixKey iProdDeriv1Key(
1851  StdRegions::eIProductWRTDerivBase1,
1852  mkey.GetShapeType(), *this);
1853 
1854  DNekMat &stdiprod0 = *GetStdMatrix(iProdDeriv0Key);
1855  DNekMat &stdiprod1 = *GetStdMatrix(iProdDeriv0Key);
1856 
1857  int rows = stdiprod0.GetRows();
1858  int cols = stdiprod1.GetColumns();
1859 
1860  DNekMatSharedPtr mat = MemoryManager<DNekMat>::
1861  AllocateSharedPtr(rows,cols);
1862  (*mat) = df[2*dir][0]*stdiprod0 +
1863  df[2*dir+1][0]*stdiprod1;
1864 
1865  returnval = MemoryManager<DNekScalMat>::
1866  AllocateSharedPtr(jac,mat);
1867  }
1868  }
1869  break;
1870  case StdRegions::eInvHybridDGHelmholtz:
1871  {
1872  NekDouble one = 1.0;
1873 
1874  MatrixKey hkey(StdRegions::eHybridDGHelmholtz,
1875  DetShapeType(), *this,
1876  mkey.GetConstFactors(), mkey.GetVarCoeffs());
1877  DNekMatSharedPtr mat = GenMatrix(hkey);
1878 
1879  mat->Invert();
1880  returnval =
1881  MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
1882  }
1883  break;
1884  case StdRegions::eInterpGauss:
1885  {
1886  DNekMatSharedPtr m_Ix;
1887  Array<OneD, NekDouble> coords(1, 0.0);
1888  StdRegions::ConstFactorMap factors = mkey.GetConstFactors();
1889  int edge = (int)factors[StdRegions::eFactorGaussEdge];
1890 
1891  coords[0] = (edge == 0 || edge == 3) ? -1.0 : 1.0;
1892 
1893  m_Ix = m_base[(edge + 1) % 2]->GetI(coords);
1894  returnval =
1895  MemoryManager<DNekScalMat>::AllocateSharedPtr(1.0,m_Ix);
1896  }
1897  break;
1898  case StdRegions::ePreconLinearSpace:
1899  {
1900  NekDouble one = 1.0;
1901  MatrixKey helmkey(
1902  StdRegions::eHelmholtz, mkey.GetShapeType(), *this,
1903  mkey.GetConstFactors(), mkey.GetVarCoeffs());
1904  DNekScalBlkMatSharedPtr helmStatCond =
1905  GetLocStaticCondMatrix(helmkey);
1906  DNekScalMatSharedPtr A =helmStatCond->GetBlock(0,0);
1907  DNekMatSharedPtr R=BuildVertexMatrix(A);
1908 
1909  returnval =
1910  MemoryManager<DNekScalMat>::AllocateSharedPtr(one, R);
1911  }
1912  break;
1913  default:
1914  {
1915  NekDouble one = 1.0;
1916  DNekMatSharedPtr mat = GenMatrix(mkey);
1917 
1918  returnval =
1919  MemoryManager<DNekScalMat>::AllocateSharedPtr(one, mat);
1920  }
1921  break;
1922  }
1923 
1924  return returnval;
1925  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Nektar::StdRegions::StdExpansion::DetShapeType
LibUtilities::ShapeType DetShapeType() const
This function returns the shape of the expansion domain.
Definition: StdExpansion.h:470
Nektar::StdRegions::StdExpansion::GenMatrix
DNekMatSharedPtr GenMatrix(const StdMatrixKey &mkey)
Definition: StdExpansion.h:1049
Nektar::LibUtilities::PointsKeyVector
std::vector< PointsKey > PointsKeyVector
Definition: Points.h:220
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::LocalRegions::Expansion::BuildVertexMatrix
DNekMatSharedPtr BuildVertexMatrix(const DNekScalMatSharedPtr &r_bnd)
Definition: Expansion.cpp:98
Nektar::StdRegions::ConstFactorMap
std::map< ConstFactorType, NekDouble > ConstFactorMap
Definition: StdRegions.hpp:251
Nektar::StdRegions::StdExpansion::GetLocStaticCondMatrix
DNekScalBlkMatSharedPtr GetLocStaticCondMatrix(const LocalRegions::MatrixKey &mkey)
Definition: StdExpansion.h:747
Nektar::DNekMatSharedPtr
boost::shared_ptr< DNekMat > DNekMatSharedPtr
Definition: NekTypeDefs.hpp:70
Nektar::StdRegions::StdExpansion::GetStdMatrix
DNekMatSharedPtr GetStdMatrix(const StdMatrixKey &mkey)
Definition: StdExpansion.h:700
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
Nektar::DNekScalBlkMatSharedPtr
boost::shared_ptr< DNekScalBlkMat > DNekScalBlkMatSharedPtr
Definition: NekTypeDefs.hpp:74
Nektar::Transpose
NekMatrix< InnerMatrixType, BlockMatrixTag > Transpose(NekMatrix< InnerMatrixType, BlockMatrixTag > &rhs)
Definition: BlockMatrix.hpp:221
Nektar::DNekMat
NekMatrix< NekDouble, StandardMatrixTag > DNekMat
Definition: NekTypeDefs.hpp:52
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
ASSERTL2
#define ASSERTL2(condition, msg)
Assert Level 2 – Debugging which is used FULLDEBUG compilation mode. This level assert is designed t...
Definition: ErrorUtil.hpp:213
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Nektar::DNekScalMat
NekMatrix< NekMatrix< NekDouble, StandardMatrixTag >, ScaledMatrixTag > DNekScalMat
Definition: NekMatrixFwd.hpp:72
DNekScalBlkMatSharedPtr Nektar::LocalRegions::QuadExp::CreateStaticCondMatrix ( const MatrixKey &  mkey)
protected

Definition at line 1928 of file QuadExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), ASSERTL2, Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::eMass, Nektar::SpatialDomains::eNoGeomType, Nektar::StdRegions::StdExpansion::GetBoundaryMap(), Nektar::StdRegions::StdExpansion::GetInteriorMap(), Nektar::LocalRegions::Expansion::GetLocMatrix(), Nektar::StdRegions::StdMatrixKey::GetMatrixType(), Nektar::StdRegions::StdMatrixKey::GetNVarCoeff(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetStdStaticCondMatrix(), Nektar::LocalRegions::Expansion::m_metricinfo, Nektar::StdRegions::StdExpansion::m_ncoeffs, and Nektar::StdRegions::StdExpansion::NumBndryCoeffs().

1930  {
1931  DNekScalBlkMatSharedPtr returnval;
1932 
1933  ASSERTL2(m_metricinfo->GetGtype()
1934  != SpatialDomains::eNoGeomType,
1935  "Geometric information is not set up");
1936 
1937  // set up block matrix system
1938  unsigned int nbdry = NumBndryCoeffs();
1939  unsigned int nint = (unsigned int)(m_ncoeffs - nbdry);
1940  unsigned int exp_size[] = {nbdry,nint};
1941  unsigned int nblks = 2;
1942  returnval = MemoryManager<DNekScalBlkMat>::
1943  AllocateSharedPtr(nblks,nblks,exp_size,exp_size);
1944  //Really need a constructor which takes Arrays
1945  NekDouble factor = 1.0;
1946 
1947  switch (mkey.GetMatrixType())
1948  {
1949  // this can only use stdregions statically condensed system
1950  // for mass matrix
1951  case StdRegions::eMass:
1952  if ((m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1953  ||(mkey.GetNVarCoeff()))
1954  {
1955  factor = 1.0;
1956  goto UseLocRegionsMatrix;
1957  }
1958  else
1959  {
1960  factor = (m_metricinfo->GetJac(GetPointsKeys()))[0];
1961  goto UseStdRegionsMatrix;
1962  }
1963  break;
1964  default: // use Deformed case for both
1965  // regular and deformed geometries
1966  factor = 1.0;
1967  goto UseLocRegionsMatrix;
1968  break;
1969  UseStdRegionsMatrix:
1970  {
1971  NekDouble invfactor = 1.0/factor;
1972  NekDouble one = 1.0;
1973  DNekBlkMatSharedPtr mat = GetStdStaticCondMatrix(mkey);
1974  DNekScalMatSharedPtr Atmp;
1975  DNekMatSharedPtr Asubmat;
1976 
1977  returnval->SetBlock(0,0,Atmp = MemoryManager<DNekScalMat>::
1978  AllocateSharedPtr(factor,Asubmat = mat->GetBlock(0,0)));
1979  returnval->SetBlock(0,1,Atmp = MemoryManager<DNekScalMat>::
1980  AllocateSharedPtr(one,Asubmat = mat->GetBlock(0,1)));
1981  returnval->SetBlock(1,0,Atmp = MemoryManager<DNekScalMat>::
1982  AllocateSharedPtr(factor,Asubmat = mat->GetBlock(1,0)));
1983  returnval->SetBlock(1,1,Atmp = MemoryManager<DNekScalMat>::
1984  AllocateSharedPtr(invfactor,Asubmat = mat->GetBlock(1,1)));
1985  }
1986  break;
1987  UseLocRegionsMatrix:
1988  {
1989  int i,j;
1990  NekDouble invfactor = 1.0/factor;
1991  NekDouble one = 1.0;
1992  DNekScalMat &mat = *GetLocMatrix(mkey);
1993  DNekMatSharedPtr A = MemoryManager<DNekMat>::
1994  AllocateSharedPtr(nbdry,nbdry);
1995  DNekMatSharedPtr B = MemoryManager<DNekMat>::
1996  AllocateSharedPtr(nbdry,nint);
1997  DNekMatSharedPtr C = MemoryManager<DNekMat>::
1998  AllocateSharedPtr(nint,nbdry);
1999  DNekMatSharedPtr D = MemoryManager<DNekMat>::
2000  AllocateSharedPtr(nint,nint);
2001 
2002  Array<OneD,unsigned int> bmap(nbdry);
2003  Array<OneD,unsigned int> imap(nint);
2004  GetBoundaryMap(bmap);
2005  GetInteriorMap(imap);
2006 
2007  for (i = 0; i < nbdry; ++i)
2008  {
2009  for(j = 0; j < nbdry; ++j)
2010  {
2011  (*A)(i,j) = mat(bmap[i],bmap[j]);
2012  }
2013 
2014  for(j = 0; j < nint; ++j)
2015  {
2016  (*B)(i,j) = mat(bmap[i],imap[j]);
2017  }
2018  }
2019 
2020  for (i = 0; i < nint; ++i)
2021  {
2022  for(j = 0; j < nbdry; ++j)
2023  {
2024  (*C)(i,j) = mat(imap[i],bmap[j]);
2025  }
2026 
2027  for(j = 0; j < nint; ++j)
2028  {
2029  (*D)(i,j) = mat(imap[i],imap[j]);
2030  }
2031  }
2032 
2033  // Calculate static condensed system
2034  if(nint)
2035  {
2036  D->Invert();
2037  (*B) = (*B)*(*D);
2038  (*A) = (*A) - (*B)*(*C);
2039  }
2040 
2041  DNekScalMatSharedPtr Atmp;
2042 
2043  returnval->SetBlock(0,0,Atmp = MemoryManager<DNekScalMat>::
2044  AllocateSharedPtr(factor, A));
2045  returnval->SetBlock(0,1,Atmp = MemoryManager<DNekScalMat>::
2046  AllocateSharedPtr(one, B));
2047  returnval->SetBlock(1,0,Atmp = MemoryManager<DNekScalMat>::
2048  AllocateSharedPtr(factor, C));
2049  returnval->SetBlock(1,1,Atmp = MemoryManager<DNekScalMat>::
2050  AllocateSharedPtr(invfactor, D));
2051 
2052  }
2053  }
2054  return returnval;
2055  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::DNekMatSharedPtr
boost::shared_ptr< DNekMat > DNekMatSharedPtr
Definition: NekTypeDefs.hpp:70
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::StdRegions::StdExpansion::GetStdStaticCondMatrix
DNekBlkMatSharedPtr GetStdStaticCondMatrix(const StdMatrixKey &mkey)
Definition: StdExpansion.h:705
Nektar::DNekScalBlkMatSharedPtr
boost::shared_ptr< DNekScalBlkMat > DNekScalBlkMatSharedPtr
Definition: NekTypeDefs.hpp:74
Nektar::StdRegions::StdExpansion::GetInteriorMap
void GetInteriorMap(Array< OneD, unsigned int > &outarray)
Definition: StdExpansion.h:821
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::DNekBlkMatSharedPtr
boost::shared_ptr< DNekBlkMat > DNekBlkMatSharedPtr
Definition: NekTypeDefs.hpp:72
Nektar::LocalRegions::Expansion::GetLocMatrix
DNekScalMatSharedPtr GetLocMatrix(const LocalRegions::MatrixKey &mkey)
Definition: Expansion.cpp:85
ASSERTL2
#define ASSERTL2(condition, msg)
Assert Level 2 – Debugging which is used FULLDEBUG compilation mode. This level assert is designed t...
Definition: ErrorUtil.hpp:213
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Nektar::DNekScalMat
NekMatrix< NekMatrix< NekDouble, StandardMatrixTag >, ScaledMatrixTag > DNekScalMat
Definition: NekMatrixFwd.hpp:72
Nektar::StdRegions::StdExpansion::GetBoundaryMap
void GetBoundaryMap(Array< OneD, unsigned int > &outarray)
Definition: StdExpansion.h:816
void Nektar::LocalRegions::QuadExp::v_ComputeEdgeNormal ( const int  edge)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1189 of file QuadExp.cpp.

References ASSERTL0, Nektar::StdRegions::eBackwards, Nektar::SpatialDomains::eDeformed, Nektar::LibUtilities::eGaussGaussLegendre, Nektar::SpatialDomains::eMovingRegular, Nektar::SpatialDomains::eRegular, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetCoordim(), Nektar::StdRegions::StdExpansion::GetEorient(), Nektar::LocalRegions::Expansion::GetGeom(), Nektar::LibUtilities::PointsKey::GetNumPoints(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetPointsType(), Nektar::LibUtilities::Interp1D(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion2D::m_edgeNormals, Vmath::Reverse(), Vmath::Sdiv(), Vmath::Smul(), v_GetEdgeInterpVals(), Vmath::Vmul(), Vmath::Vsqrt(), Vmath::Vvtvp(), and Vmath::Zero().

1190  {
1191  int i;
1192  const SpatialDomains::GeomFactorsSharedPtr & geomFactors =
1193  GetGeom()->GetMetricInfo();
1194  SpatialDomains::GeomType type = geomFactors->GetGtype();
1195  LibUtilities::PointsKeyVector ptsKeys = GetPointsKeys();
1196  const Array<TwoD, const NekDouble> & df = geomFactors->GetDerivFactors(ptsKeys);
1197  const Array<OneD, const NekDouble> & jac = geomFactors->GetJac(ptsKeys);
1198  int nqe;
1199  if (edge == 0 || edge == 2)
1200  {
1201  nqe = m_base[0]->GetNumPoints();
1202  }
1203  else
1204  {
1205  nqe = m_base[1]->GetNumPoints();
1206  }
1207  int vCoordDim = GetCoordim();
1208 
1209  m_edgeNormals[edge] = Array<OneD, Array<OneD, NekDouble> >
1210  (vCoordDim);
1211  Array<OneD, Array<OneD, NekDouble> > &normal = m_edgeNormals[edge];
1212  for (i = 0; i < vCoordDim; ++i)
1213  {
1214  normal[i] = Array<OneD, NekDouble>(nqe);
1215  }
1216 
1217  // Regular geometry case
1218  if ((type == SpatialDomains::eRegular)||
1219  (type == SpatialDomains::eMovingRegular))
1220  {
1221  NekDouble fac;
1222  // Set up normals
1223  switch (edge)
1224  {
1225  case 0:
1226  for (i = 0; i < vCoordDim; ++i)
1227  {
1228  Vmath::Fill(nqe, -df[2*i+1][0], normal[i], 1);
1229  }
1230  break;
1231  case 1:
1232  for (i = 0; i < vCoordDim; ++i)
1233  {
1234  Vmath::Fill(nqe, df[2*i][0], normal[i], 1);
1235  }
1236  break;
1237  case 2:
1238  for (i = 0; i < vCoordDim; ++i)
1239  {
1240  Vmath::Fill(nqe, df[2*i+1][0], normal[i], 1);
1241  }
1242  break;
1243  case 3:
1244  for (i = 0; i < vCoordDim; ++i)
1245  {
1246  Vmath::Fill(nqe, -df[2*i][0], normal[i], 1);
1247  }
1248  break;
1249  default:
1250  ASSERTL0(false, "edge is out of range (edge < 4)");
1251  }
1252 
1253  // normalise
1254  fac = 0.0;
1255  for (i =0 ; i < vCoordDim; ++i)
1256  {
1257  fac += normal[i][0]*normal[i][0];
1258  }
1259  fac = 1.0/sqrt(fac);
1260  for (i = 0; i < vCoordDim; ++i)
1261  {
1262  Vmath::Smul(nqe, fac, normal[i], 1,normal[i], 1);
1263  }
1264  }
1265  else // Set up deformed normals
1266  {
1267  int j;
1268 
1269  int nquad0 = ptsKeys[0].GetNumPoints();
1270  int nquad1 = ptsKeys[1].GetNumPoints();
1271 
1272  LibUtilities::PointsKey from_key;
1273 
1274  Array<OneD,NekDouble> normals(vCoordDim*max(nquad0,nquad1),0.0);
1275  Array<OneD,NekDouble> edgejac(vCoordDim*max(nquad0,nquad1),0.0);
1276 
1277  // Extract Jacobian along edges and recover local
1278  // derivates (dx/dr) for polynomial interpolation by
1279  // multiplying m_gmat by jacobian
1280 
1281  // Implementation for all the basis except Gauss points
1282  if (m_base[0]->GetPointsType() !=
1283  LibUtilities::eGaussGaussLegendre
1284  && m_base[1]->GetPointsType() !=
1285  LibUtilities::eGaussGaussLegendre)
1286  {
1287  switch (edge)
1288  {
1289  case 0:
1290  for (j = 0; j < nquad0; ++j)
1291  {
1292  edgejac[j] = jac[j];
1293  for (i = 0; i < vCoordDim; ++i)
1294  {
1295  normals[i*nquad0+j] =
1296  -df[2*i+1][j]*edgejac[j];
1297  }
1298  }
1299  from_key = ptsKeys[0];
1300  break;
1301  case 1:
1302  for (j = 0; j < nquad1; ++j)
1303  {
1304  edgejac[j] = jac[nquad0*j+nquad0-1];
1305  for (i = 0; i < vCoordDim; ++i)
1306  {
1307  normals[i*nquad1+j] =
1308  df[2*i][nquad0*j + nquad0-1]
1309  *edgejac[j];
1310  }
1311  }
1312  from_key = ptsKeys[1];
1313  break;
1314  case 2:
1315  for (j = 0; j < nquad0; ++j)
1316  {
1317  edgejac[j] = jac[nquad0*(nquad1-1)+j];
1318  for (i = 0; i < vCoordDim; ++i)
1319  {
1320  normals[i*nquad0+j] =
1321  (df[2*i+1][nquad0*(nquad1-1)+j])
1322  *edgejac[j];
1323  }
1324  }
1325  from_key = ptsKeys[0];
1326  break;
1327  case 3:
1328  for (j = 0; j < nquad1; ++j)
1329  {
1330  edgejac[j] = jac[nquad0*j];
1331  for (i = 0; i < vCoordDim; ++i)
1332  {
1333  normals[i*nquad1+j] =
1334  -df[2*i][nquad0*j]*edgejac[j];
1335  }
1336  }
1337  from_key = ptsKeys[1];
1338  break;
1339  default:
1340  ASSERTL0(false,"edge is out of range (edge < 3)");
1341  }
1342  }
1343  else
1344  {
1345  int nqtot = nquad0 * nquad1;
1346  Array<OneD, NekDouble> tmp_gmat(nqtot, 0.0);
1347  Array<OneD, NekDouble> tmp_gmat_edge(nqe, 0.0);
1348 
1349  switch (edge)
1350  {
1351  case 0:
1352  for (j = 0; j < nquad0; ++j)
1353  {
1354  for (i = 0; i < vCoordDim; ++i)
1355  {
1356  Vmath::Vmul(nqtot,
1357  &(df[2*i+1][0]), 1,
1358  &jac[0], 1,
1359  &(tmp_gmat[0]), 1);
1360  QuadExp::v_GetEdgeInterpVals(
1361  edge, tmp_gmat, tmp_gmat_edge);
1362  normals[i*nquad0+j] = -tmp_gmat_edge[j];
1363  }
1364  }
1365  from_key = ptsKeys[0];
1366  break;
1367  case 1:
1368  for (j = 0; j < nquad1; ++j)
1369  {
1370  for (i = 0; i < vCoordDim; ++i)
1371  {
1372  Vmath::Vmul(nqtot,
1373  &(df[2*i][0]), 1,
1374  &jac[0], 1,
1375  &(tmp_gmat[0]), 1);
1376  QuadExp::v_GetEdgeInterpVals(
1377  edge, tmp_gmat, tmp_gmat_edge);
1378  normals[i*nquad1+j] = tmp_gmat_edge[j];
1379  }
1380  }
1381  from_key = ptsKeys[1];
1382  break;
1383  case 2:
1384  for (j = 0; j < nquad0; ++j)
1385  {
1386  for (i = 0; i < vCoordDim; ++i)
1387  {
1388  Vmath::Vmul(nqtot,
1389  &(df[2*i+1][0]), 1,
1390  &jac[0], 1,
1391  &(tmp_gmat[0]), 1);
1392  QuadExp::v_GetEdgeInterpVals(
1393  edge, tmp_gmat, tmp_gmat_edge);
1394  normals[i*nquad0+j] = tmp_gmat_edge[j];
1395  }
1396  }
1397  from_key = ptsKeys[0];
1398  break;
1399  case 3:
1400  for (j = 0; j < nquad1; ++j)
1401  {
1402  for (i = 0; i < vCoordDim; ++i)
1403  {
1404  Vmath::Vmul(nqtot,
1405  &(df[2*i][0]), 1,
1406  &jac[0], 1,
1407  &(tmp_gmat[0]) ,1);
1408  QuadExp::v_GetEdgeInterpVals(
1409  edge, tmp_gmat, tmp_gmat_edge);
1410  normals[i*nquad1+j] = -tmp_gmat_edge[j];
1411  }
1412  }
1413  from_key = ptsKeys[1];
1414  break;
1415  default:
1416  ASSERTL0(false,"edge is out of range (edge < 3)");
1417  }
1418  }
1419 
1420  int nq = from_key.GetNumPoints();
1421  Array<OneD,NekDouble> work(nqe,0.0);
1422 
1423  // interpolate Jacobian and invert
1424  LibUtilities::Interp1D(
1425  from_key,jac, m_base[0]->GetPointsKey(), work);
1426  Vmath::Sdiv(nq,1.0,&work[0],1,&work[0],1);
1427 
1428  // interpolate
1429  for (i = 0; i < GetCoordim(); ++i)
1430  {
1431  LibUtilities::Interp1D(
1432  from_key,&normals[i*nq],
1433  m_base[0]->GetPointsKey(),
1434  &normal[i][0]);
1435  Vmath::Vmul(nqe, work, 1, normal[i], 1, normal[i], 1);
1436  }
1437 
1438  //normalise normal vectors
1439  Vmath::Zero(nqe,work,1);
1440  for (i = 0; i < GetCoordim(); ++i)
1441  {
1442  Vmath::Vvtvp(nqe,
1443  normal[i], 1,
1444  normal[i],1 ,
1445  work, 1,
1446  work, 1);
1447  }
1448 
1449  Vmath::Vsqrt(nqe,work,1,work,1);
1450  Vmath::Sdiv(nqe,1.0,work,1,work,1);
1451 
1452  for (i = 0; i < GetCoordim(); ++i)
1453  {
1454  Vmath::Vmul(nqe, normal[i], 1, work, 1, normal[i], 1);
1455  }
1456 
1457  // Reverse direction so that points are in
1458  // anticlockwise direction if edge >=2
1459  if (edge >= 2)
1460  {
1461  for (i = 0; i < GetCoordim(); ++i)
1462  {
1463  Vmath::Reverse(nqe, normal[i], 1, normal[i], 1);
1464  }
1465  }
1466  }
1467  if (GetGeom()->GetEorient(edge) == StdRegions::eBackwards)
1468  {
1469  for (i = 0; i < vCoordDim; ++i)
1470  {
1471  if (geomFactors->GetGtype() == SpatialDomains::eDeformed)
1472  {
1473  Vmath::Reverse(nqe, normal[i], 1, normal[i],1);
1474  }
1475  }
1476  }
1477  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::LibUtilities::PointsKeyVector
std::vector< PointsKey > PointsKeyVector
Definition: Points.h:220
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::LocalRegions::Expansion2D::m_edgeNormals
std::map< int, StdRegions::NormalVector > m_edgeNormals
Definition: Expansion2D.h:135
Nektar::StdRegions::StdExpansion::GetEorient
StdRegions::Orientation GetEorient(int edge)
Definition: StdExpansion.h:762
Nektar::LocalRegions::QuadExp::v_GetEdgeInterpVals
virtual void v_GetEdgeInterpVals(const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: QuadExp.cpp:815
Vmath::Sdiv
void Sdiv(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha/y.
Definition: Vmath.cpp:257
Nektar::LibUtilities::eGaussGaussLegendre
1D Gauss-Gauss-Legendre quadrature points
Definition: PointsType.h:47
Vmath::Reverse
void Reverse(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1071
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::LocalRegions::Expansion::GetGeom
SpatialDomains::GeometrySharedPtr GetGeom() const
Definition: Expansion.cpp:150
Nektar::SpatialDomains::GeomFactorsSharedPtr
boost::shared_ptr< GeomFactors > GeomFactorsSharedPtr
Pointer to a GeomFactors object.
Definition: GeomFactors.h:62
Nektar::SpatialDomains::eRegular
Geometry is straight-sided with constant geometric factors.
Definition: SpatialDomains.hpp:55
Nektar::LibUtilities::Interp1D
void Interp1D(const BasisKey &fbasis0, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, Array< OneD, NekDouble > &to)
this function interpolates a 1D function evaluated at the quadrature points of the basis fbasis0 to ...
Definition: Interp.cpp:54
Nektar::SpatialDomains::GeomType
GeomType
Indicates the type of element geometry.
Definition: SpatialDomains.hpp:52
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
Nektar::StdRegions::StdExpansion::GetPointsType
LibUtilities::PointsType GetPointsType(const int dir) const
This function returns the type of quadrature points used in the dir direction.
Definition: StdExpansion.h:216
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::QuadExp::v_ComputeLaplacianMetric ( )
protectedvirtual

Reimplemented from Nektar::LocalRegions::Expansion.

Definition at line 2272 of file QuadExp.cpp.

References Nektar::LocalRegions::Expansion::ComputeQuadratureMetric(), Nektar::SpatialDomains::eDeformed, Nektar::LocalRegions::eMetricLaplacian00, Nektar::LocalRegions::eMetricLaplacian01, Nektar::LocalRegions::eMetricLaplacian02, Nektar::LocalRegions::eMetricLaplacian11, Nektar::LocalRegions::eMetricLaplacian12, Nektar::LocalRegions::eMetricLaplacian22, Nektar::LocalRegions::eMetricQuadrature, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetTotPoints(), Nektar::LocalRegions::Expansion::m_metricinfo, Nektar::LocalRegions::Expansion::m_metrics, Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric(), and Vmath::Vcopy().

2273  {
2274  if (m_metrics.count(eMetricQuadrature) == 0)
2275  {
2276  ComputeQuadratureMetric();
2277  }
2278 
2279  const SpatialDomains::GeomType type = m_metricinfo->GetGtype();
2280  const unsigned int nqtot = GetTotPoints();
2281  const unsigned int dim = 2;
2282  const MetricType m[3][3] = { {eMetricLaplacian00, eMetricLaplacian01, eMetricLaplacian02},
2283  {eMetricLaplacian01, eMetricLaplacian11, eMetricLaplacian12},
2284  {eMetricLaplacian02, eMetricLaplacian12, eMetricLaplacian22}
2285  };
2286 
2287  const Array<TwoD, const NekDouble> gmat =
2288  m_metricinfo->GetGmat(GetPointsKeys());
2289  for (unsigned int i = 0; i < dim; ++i)
2290  {
2291  for (unsigned int j = i; j < dim; ++j)
2292  {
2293  m_metrics[m[i][j]] = Array<OneD, NekDouble>(nqtot);
2294  if (type == SpatialDomains::eDeformed)
2295  {
2296  Vmath::Vcopy(nqtot, &gmat[i*dim+j][0], 1,
2297  &m_metrics[m[i][j]][0], 1);
2298  }
2299  else
2300  {
2301  Vmath::Fill(nqtot, gmat[i*dim+j][0],
2302  &m_metrics[m[i][j]][0], 1);
2303  }
2304  MultiplyByQuadratureMetric(m_metrics[m[i][j]],
2305  m_metrics[m[i][j]]);
2306 
2307  }
2308  }
2309  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric
void MultiplyByQuadratureMetric(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:942
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::StdRegions::StdExpansion::GetTotPoints
int GetTotPoints() const
This function returns the total number of quadrature points used in the element.
Definition: StdExpansion.h:141
Nektar::SpatialDomains::GeomType
GeomType
Indicates the type of element geometry.
Definition: SpatialDomains.hpp:52
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
DNekMatSharedPtr Nektar::LocalRegions::QuadExp::v_CreateStdMatrix ( const StdRegions::StdMatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 1603 of file QuadExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::StdRegions::StdExpansion::m_base.

1605  {
1606  LibUtilities::BasisKey bkey0 = m_base[0]->GetBasisKey();
1607  LibUtilities::BasisKey bkey1 = m_base[1]->GetBasisKey();
1608  StdRegions::StdQuadExpSharedPtr tmp =
1609  MemoryManager<StdQuadExp>::AllocateSharedPtr(bkey0,bkey1);
1610  return tmp->GetStdMatrix(mkey);
1611  }
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::StdRegions::StdQuadExpSharedPtr
boost::shared_ptr< StdQuadExp > StdQuadExpSharedPtr
Definition: StdQuadExp.h:262
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
void Nektar::LocalRegions::QuadExp::v_DropLocStaticCondMatrix ( const MatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 2070 of file QuadExp.cpp.

References m_staticCondMatrixManager.

2071  {
2072  m_staticCondMatrixManager.DeleteObject(mkey);
2073  }
Nektar::LocalRegions::QuadExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: QuadExp.h:286
void Nektar::LocalRegions::QuadExp::v_ExtractDataToCoeffs ( const NekDouble *  data,
const std::vector< unsigned int > &  nummodes,
const int  nmode_offset,
NekDouble *  coeffs 
)
protectedvirtual

Unpack data from input file assuming it comes from the same expansion type.

See also
StdExpansion::ExtractDataToCoeffs

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1491 of file QuadExp.cpp.

References ASSERTL0, ASSERTL1, Nektar::LibUtilities::eGauss_Lagrange, Nektar::LibUtilities::eGaussGaussLegendre, Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::eGLL_Lagrange, Nektar::LibUtilities::eModified_A, Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::LibUtilities::Interp2D(), Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion::m_ncoeffs, Vmath::Vcopy(), and Vmath::Zero().

1496  {
1497  int data_order0 = nummodes[mode_offset];
1498  int fillorder0 = std::min(m_base[0]->GetNumModes(),data_order0);
1499 
1500  int data_order1 = nummodes[mode_offset + 1];
1501  int order1 = m_base[1]->GetNumModes();
1502  int fillorder1 = min(order1,data_order1);
1503 
1504  switch (m_base[0]->GetBasisType())
1505  {
1506  case LibUtilities::eModified_A:
1507  {
1508  int i;
1509  int cnt = 0;
1510  int cnt1 = 0;
1511 
1512  ASSERTL1(m_base[1]->GetBasisType() ==
1513  LibUtilities::eModified_A,
1514  "Extraction routine not set up for this basis");
1515 
1516  Vmath::Zero(m_ncoeffs,coeffs,1);
1517  for (i = 0; i < fillorder0; ++i)
1518  {
1519  Vmath::Vcopy(fillorder1, data + cnt, 1, coeffs +cnt1, 1);
1520  cnt += data_order1;
1521  cnt1 += order1;
1522  }
1523  }
1524  break;
1525  case LibUtilities::eGLL_Lagrange:
1526  {
1527  // Assume that input is also Gll_Lagrange but no way to check;
1528  LibUtilities::PointsKey
1529  p0(nummodes[0], LibUtilities::eGaussLobattoLegendre);
1530  LibUtilities::PointsKey
1531  p1(nummodes[1], LibUtilities::eGaussLobattoLegendre);
1532  LibUtilities::Interp2D(p0, p1, data,
1533  m_base[0]->GetPointsKey(),
1534  m_base[1]->GetPointsKey(),
1535  coeffs);
1536  }
1537  break;
1538  case LibUtilities::eGauss_Lagrange:
1539  {
1540  // Assume that input is also Gll_Lagrange but no way to check;
1541  LibUtilities::PointsKey
1542  p0(nummodes[0],LibUtilities::eGaussGaussLegendre);
1543  LibUtilities::PointsKey
1544  p1(nummodes[1],LibUtilities::eGaussGaussLegendre);
1545  LibUtilities::Interp2D(p0, p1, data,
1546  m_base[0]->GetPointsKey(),
1547  m_base[1]->GetPointsKey(),
1548  coeffs);
1549  }
1550  break;
1551  default:
1552  ASSERTL0(false,
1553  "basis is either not set up or not hierarchicial");
1554  }
1555  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::LibUtilities::eModified_A
Principle Modified Functions .
Definition: BasisType.h:49
Nektar::LibUtilities::eGauss_Lagrange
Lagrange Polynomials using the Gauss points .
Definition: BasisType.h:54
Nektar::LibUtilities::eGaussGaussLegendre
1D Gauss-Gauss-Legendre quadrature points
Definition: PointsType.h:47
Nektar::LibUtilities::Interp2D
void Interp2D(const BasisKey &fbasis0, const BasisKey &fbasis1, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, Array< OneD, NekDouble > &to)
this function interpolates a 2D function evaluated at the quadrature points of the 2D basis...
Definition: Interp.cpp:116
Nektar::StdRegions::StdExpansion::GetBasisType
LibUtilities::BasisType GetBasisType(const int dir) const
This function returns the type of basis used in the dir direction.
Definition: StdExpansion.h:165
Nektar::LibUtilities::eGLL_Lagrange
Lagrange for SEM basis .
Definition: BasisType.h:53
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Nektar::LibUtilities::eGaussLobattoLegendre
1D Gauss-Lobatto-Legendre quadrature points
Definition: PointsType.h:50
void Nektar::LocalRegions::QuadExp::v_FwdTrans ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Transform a given function from physical quadrature space to coefficient space.

See also
StdExpansion::FwdTrans

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 260 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::eCopy, Nektar::StdRegions::eInvMass, Nektar::eWrapper, Nektar::StdRegions::StdExpansion::IProductWRTBase(), Nektar::StdRegions::StdExpansion::m_base, m_matrixManager, Nektar::StdRegions::StdExpansion::m_ncoeffs, and Vmath::Vcopy().

263  {
264  if ((m_base[0]->Collocation())&&(m_base[1]->Collocation()))
265  {
266  Vmath::Vcopy(m_ncoeffs, inarray, 1, outarray, 1);
267  }
268  else
269  {
270  IProductWRTBase(inarray,outarray);
271 
272  // get Mass matrix inverse
273  MatrixKey masskey(StdRegions::eInvMass,
274  DetShapeType(),*this);
275  DNekScalMatSharedPtr matsys = m_matrixManager[masskey];
276 
277  // copy inarray in case inarray == outarray
278  NekVector<NekDouble> in(m_ncoeffs,outarray,eCopy);
279  NekVector<NekDouble> out(m_ncoeffs,outarray,eWrapper);
280 
281  out = (*matsys)*in;
282  }
283  }
Nektar::StdRegions::StdExpansion::DetShapeType
LibUtilities::ShapeType DetShapeType() const
This function returns the shape of the expansion domain.
Definition: StdExpansion.h:470
Nektar::StdRegions::StdExpansion::IProductWRTBase
void IProductWRTBase(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
this function calculates the inner product of a given function f with the different modes of the expa...
Definition: StdExpansion.h:629
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
void Nektar::LocalRegions::QuadExp::v_FwdTrans_BndConstrained ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 286 of file QuadExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eBackwards, Nektar::StdRegions::eMass, Nektar::StdRegions::StdExpansion::GetEdgeToElementMap(), Nektar::StdRegions::StdExpansion::GetEorient(), Nektar::LocalRegions::Expansion2D::GetGeom2D(), Nektar::StdRegions::StdExpansion::GetInteriorMap(), Nektar::StdRegions::StdExpansion::IProductWRTBase(), Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion::m_ncoeffs, m_staticCondMatrixManager, Nektar::StdRegions::StdExpansion::MassMatrixOp(), Nektar::StdRegions::StdExpansion::NumBndryCoeffs(), sign, Vmath::Vcopy(), and Vmath::Vsub().

289  {
290  if ((m_base[0]->Collocation())&&(m_base[1]->Collocation()))
291  {
292  Vmath::Vcopy(m_ncoeffs, inarray, 1, outarray, 1);
293  }
294  else
295  {
296  int i,j;
297  int npoints[2] = {m_base[0]->GetNumPoints(),
298  m_base[1]->GetNumPoints()};
299  int nmodes[2] = {m_base[0]->GetNumModes(),
300  m_base[1]->GetNumModes()};
301 
302  fill(outarray.get(), outarray.get()+m_ncoeffs, 0.0 );
303 
304  Array<OneD, NekDouble> physEdge[4];
305  Array<OneD, NekDouble> coeffEdge[4];
306  StdRegions::Orientation orient[4];
307  for (i = 0; i < 4; i++)
308  {
309  physEdge[i] = Array<OneD, NekDouble>(npoints[i%2]);
310  coeffEdge[i] = Array<OneD, NekDouble>(nmodes[i%2]);
311  orient[i] = GetEorient(i);
312  }
313 
314  for (i = 0; i < npoints[0]; i++)
315  {
316  physEdge[0][i] = inarray[i];
317  physEdge[2][i] = inarray[npoints[0]*npoints[1]-1-i];
318  }
319 
320  for (i = 0; i < npoints[1]; i++)
321  {
322  physEdge[1][i] =
323  inarray[npoints[0]-1+i*npoints[0]];
324  physEdge[3][i] =
325  inarray[(npoints[1]-1)*npoints[0]-i*npoints[0]];
326  }
327 
328  for (i = 0; i < 4; i++)
329  {
330  if ( orient[i] == StdRegions::eBackwards )
331  {
332  reverse((physEdge[i]).get(),
333  (physEdge[i]).get() + npoints[i%2] );
334  }
335  }
336 
337  SegExpSharedPtr segexp[4];
338  for (i = 0; i < 4; i++)
339  {
340  segexp[i] = MemoryManager<LocalRegions::SegExp>::
341  AllocateSharedPtr(
342  m_base[i%2]->GetBasisKey(),GetGeom2D()->GetEdge(i));
343  }
344 
345  Array<OneD, unsigned int> mapArray;
346  Array<OneD, int> signArray;
347  NekDouble sign;
348 
349  for (i = 0; i < 4; i++)
350  {
351  segexp[i%2]->FwdTrans_BndConstrained(
352  physEdge[i],coeffEdge[i]);
353 
354  GetEdgeToElementMap(i,orient[i],mapArray,signArray);
355  for (j=0; j < nmodes[i%2]; j++)
356  {
357  sign = (NekDouble) signArray[j];
358  outarray[ mapArray[j] ] = sign * coeffEdge[i][j];
359  }
360  }
361 
362  int nBoundaryDofs = NumBndryCoeffs();
363  int nInteriorDofs = m_ncoeffs - nBoundaryDofs;
364 
365  if (nInteriorDofs > 0) {
366  Array<OneD, NekDouble> tmp0(m_ncoeffs);
367  Array<OneD, NekDouble> tmp1(m_ncoeffs);
368 
369  StdRegions::StdMatrixKey
370  stdmasskey(StdRegions::eMass,DetShapeType(),*this);
371  MassMatrixOp(outarray,tmp0,stdmasskey);
372  IProductWRTBase(inarray,tmp1);
373 
374  Vmath::Vsub(m_ncoeffs, tmp1, 1, tmp0, 1, tmp1, 1);
375 
376  // get Mass matrix inverse (only of interior DOF)
377  // use block (1,1) of the static condensed system
378  // note: this block alreay contains the inverse matrix
379  MatrixKey
380  masskey(StdRegions::eMass,DetShapeType(),*this);
381  DNekScalMatSharedPtr matsys =
382  (m_staticCondMatrixManager[masskey])->GetBlock(1,1);
383 
384  Array<OneD, NekDouble> rhs(nInteriorDofs);
385  Array<OneD, NekDouble> result(nInteriorDofs);
386 
387  GetInteriorMap(mapArray);
388 
389  for (i = 0; i < nInteriorDofs; i++)
390  {
391  rhs[i] = tmp1[ mapArray[i] ];
392  }
393 
394  Blas::Dgemv('N', nInteriorDofs, nInteriorDofs,
395  matsys->Scale(),
396  &((matsys->GetOwnedMatrix())->GetPtr())[0],
397  nInteriorDofs,rhs.get(),1,0.0,result.get(),1);
398 
399  for (i = 0; i < nInteriorDofs; i++)
400  {
401  outarray[ mapArray[i] ] = result[i];
402  }
403  }
404  }
405 
406  }
Nektar::StdRegions::StdExpansion::DetShapeType
LibUtilities::ShapeType DetShapeType() const
This function returns the shape of the expansion domain.
Definition: StdExpansion.h:470
Nektar::StdRegions::StdExpansion::MassMatrixOp
void MassMatrixOp(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
Definition: StdExpansion.h:971
Nektar::LocalRegions::QuadExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: QuadExp.h:286
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
sign
#define sign(a, b)
return the sign(b)*a
Definition: Polylib.cpp:22
Nektar::StdRegions::StdExpansion::IProductWRTBase
void IProductWRTBase(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
this function calculates the inner product of a given function f with the different modes of the expa...
Definition: StdExpansion.h:629
Nektar::StdRegions::StdExpansion::GetEorient
StdRegions::Orientation GetEorient(int edge)
Definition: StdExpansion.h:762
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::LocalRegions::SegExpSharedPtr
boost::shared_ptr< SegExp > SegExpSharedPtr
Definition: SegExp.h:266
Nektar::LocalRegions::Expansion2D::GetGeom2D
SpatialDomains::Geometry2DSharedPtr GetGeom2D() const
Definition: Expansion2D.h:269
Nektar::StdRegions::StdExpansion::GetInteriorMap
void GetInteriorMap(Array< OneD, unsigned int > &outarray)
Definition: StdExpansion.h:821
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Vmath::Vsub
void Vsub(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Subtract vector z = x-y.
Definition: Vmath.cpp:329
Nektar::StdRegions::StdExpansion::GetEdgeToElementMap
void GetEdgeToElementMap(const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int P=-1)
Definition: StdExpansion.h:846
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
void Nektar::LocalRegions::QuadExp::v_GeneralMatrixOp_MatOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Definition at line 2145 of file QuadExp.cpp.

References Nektar::LocalRegions::Expansion::GetLocMatrix(), Nektar::StdRegions::StdExpansion::m_ncoeffs, and Vmath::Vcopy().

2149  {
2150  MatrixKey newkey(mkey);
2151  DNekScalMatSharedPtr mat = GetLocMatrix(newkey);
2152 
2153  if (inarray.get() == outarray.get())
2154  {
2155  Array<OneD,NekDouble> tmp(m_ncoeffs);
2156  Vmath::Vcopy(m_ncoeffs,inarray.get(),1,tmp.get(),1);
2157 
2158  Blas::Dgemv('N',m_ncoeffs,m_ncoeffs, mat->Scale(),
2159  (mat->GetOwnedMatrix())->GetPtr().get(), m_ncoeffs,
2160  tmp.get(), 1, 0.0, outarray.get(), 1);
2161  }
2162  else
2163  {
2164  Blas::Dgemv('N',m_ncoeffs,m_ncoeffs,mat->Scale(),
2165  (mat->GetOwnedMatrix())->GetPtr().get(), m_ncoeffs,
2166  inarray.get(), 1, 0.0, outarray.get(), 1);
2167  }
2168  }
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::LocalRegions::Expansion::GetLocMatrix
DNekScalMatSharedPtr GetLocMatrix(const LocalRegions::MatrixKey &mkey)
Definition: Expansion.cpp:85
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
DNekMatSharedPtr Nektar::LocalRegions::QuadExp::v_GenMatrix ( const StdRegions::StdMatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 1582 of file QuadExp.cpp.

References Nektar::StdRegions::eHybridDGHelmBndLam, Nektar::StdRegions::eHybridDGHelmholtz, Nektar::StdRegions::eHybridDGLamToQ0, Nektar::StdRegions::eHybridDGLamToQ1, Nektar::StdRegions::eHybridDGLamToQ2, Nektar::StdRegions::eHybridDGLamToU, Nektar::StdRegions::eInvLaplacianWithUnityMean, Nektar::StdRegions::StdMatrixKey::GetMatrixType(), and Nektar::LocalRegions::Expansion2D::v_GenMatrix().

1584  {
1585  DNekMatSharedPtr returnval;
1586  switch (mkey.GetMatrixType())
1587  {
1588  case StdRegions::eHybridDGHelmholtz:
1589  case StdRegions::eHybridDGLamToU:
1590  case StdRegions::eHybridDGLamToQ0:
1591  case StdRegions::eHybridDGLamToQ1:
1592  case StdRegions::eHybridDGLamToQ2:
1593  case StdRegions::eHybridDGHelmBndLam:
1594  case StdRegions::eInvLaplacianWithUnityMean:
1595  returnval = Expansion2D::v_GenMatrix(mkey);
1596  break;
1597  default:
1598  returnval = StdQuadExp::v_GenMatrix(mkey);
1599  }
1600  return returnval;
1601  }
Nektar::DNekMatSharedPtr
boost::shared_ptr< DNekMat > DNekMatSharedPtr
Definition: NekTypeDefs.hpp:70
Nektar::LocalRegions::Expansion2D::v_GenMatrix
virtual DNekMatSharedPtr v_GenMatrix(const StdRegions::StdMatrixKey &mkey)
Definition: Expansion2D.cpp:641
const LibUtilities::BasisSharedPtr & Nektar::LocalRegions::QuadExp::v_GetBasis ( int  dir) const
protectedvirtual

Definition at line 1570 of file QuadExp.cpp.

References ASSERTL1, and Nektar::StdRegions::StdExpansion::m_base.

1571  {
1572  ASSERTL1(dir >= 0 &&dir <= 1, "input dir is out of range");
1573  return m_base[dir];
1574  }
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
StdRegions::Orientation Nektar::LocalRegions::QuadExp::v_GetCartesianEorient ( int  edge)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1564 of file QuadExp.cpp.

References Nektar::LocalRegions::Expansion2D::GetGeom2D().

1565  {
1566  return GetGeom2D()->GetCartesianEorient(edge);
1567  }
Nektar::LocalRegions::Expansion2D::GetGeom2D
SpatialDomains::Geometry2DSharedPtr GetGeom2D() const
Definition: Expansion2D.h:269
void Nektar::LocalRegions::QuadExp::v_GetCoord ( const Array< OneD, const NekDouble > &  Lcoords,
Array< OneD, NekDouble > &  coords 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 628 of file QuadExp.cpp.

References ASSERTL1, and Nektar::LocalRegions::Expansion::m_geom.

630  {
631  int i;
632 
633  ASSERTL1(Lcoords[0] >= -1.0 && Lcoords[1] <= 1.0 &&
634  Lcoords[1] >= -1.0 && Lcoords[1] <=1.0,
635  "Local coordinates are not in region [-1,1]");
636 
637  m_geom->FillGeom();
638  for (i = 0; i < m_geom->GetCoordim(); ++i)
639  {
640  coords[i] = m_geom->GetCoord(i,Lcoords);
641  }
642  }
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
int Nektar::LocalRegions::QuadExp::v_GetCoordim ( void  )
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion2D.

Definition at line 1485 of file QuadExp.cpp.

References Nektar::LocalRegions::Expansion::m_geom.

1486  {
1487  return m_geom->GetCoordim();
1488  }
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
void Nektar::LocalRegions::QuadExp::v_GetCoords ( Array< OneD, NekDouble > &  coords_1,
Array< OneD, NekDouble > &  coords_2,
Array< OneD, NekDouble > &  coords_3 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 619 of file QuadExp.cpp.

References Nektar::LocalRegions::Expansion::v_GetCoords().

623  {
624  Expansion::v_GetCoords(coords_0, coords_1, coords_2);
625  }
Nektar::LocalRegions::Expansion::v_GetCoords
virtual void v_GetCoords(Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2, Array< OneD, NekDouble > &coords_3)
Definition: Expansion.cpp:213
void Nektar::LocalRegions::QuadExp::v_GetEdgeInterpVals ( const int  edge,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 815 of file QuadExp.cpp.

References ASSERTL0, Vmath::Ddot(), Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eFactorGaussEdge, Nektar::StdRegions::eInterpGauss, Nektar::StdRegions::StdExpansion::m_base, and m_matrixManager.

Referenced by v_ComputeEdgeNormal(), v_GetEdgePhysVals(), and v_GetEdgeQFactors().

818  {
819  int i;
820  int nq0 = m_base[0]->GetNumPoints();
821  int nq1 = m_base[1]->GetNumPoints();
822 
823  StdRegions::ConstFactorMap factors;
824  factors[StdRegions::eFactorGaussEdge] = edge;
825 
826  StdRegions::StdMatrixKey key(
827  StdRegions::eInterpGauss,
828  DetShapeType(),*this,factors);
829 
830  DNekScalMatSharedPtr mat_gauss = m_matrixManager[key];
831 
832  switch (edge)
833  {
834  case 0:
835  {
836  for (i = 0; i < nq0; i++)
837  {
838  outarray[i] = Blas::Ddot(
839  nq1, mat_gauss->GetOwnedMatrix()->GetPtr().get(),
840  1, &inarray[i], nq0);
841  }
842  break;
843  }
844  case 1:
845  {
846  for (i = 0; i < nq1; i++)
847  {
848  outarray[i] = Blas::Ddot(
849  nq0, mat_gauss->GetOwnedMatrix()->GetPtr().get(),
850  1, &inarray[i * nq0], 1);
851  }
852  break;
853  }
854  case 2:
855  {
856  for (i = 0; i < nq0; i++)
857  {
858  outarray[i] = Blas::Ddot(
859  nq1, mat_gauss->GetOwnedMatrix()->GetPtr().get(),
860  1, &inarray[i], nq0);
861  }
862  break;
863  }
864  case 3:
865  {
866  for (i = 0; i < nq1; i++)
867  {
868  outarray[i] = Blas::Ddot(
869  nq0, mat_gauss->GetOwnedMatrix()->GetPtr().get(),
870  1, &inarray[i * nq0], 1);
871  }
872  break;
873  }
874  default:
875  ASSERTL0(false, "edge value (< 3) is out of range");
876  break;
877  }
878  }
Nektar::StdRegions::StdExpansion::DetShapeType
LibUtilities::ShapeType DetShapeType() const
This function returns the shape of the expansion domain.
Definition: StdExpansion.h:470
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::StdRegions::ConstFactorMap
std::map< ConstFactorType, NekDouble > ConstFactorMap
Definition: StdRegions.hpp:251
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
Vmath::Ddot
T Ddot(int n, const Array< OneD, const T > &w, const int incw, const Array< OneD, const T > &x, const int incx, const Array< OneD, const int > &y, const int incy)
Definition: VmathArray.hpp:434
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
void Nektar::LocalRegions::QuadExp::v_GetEdgePhysMap ( const int  edge,
Array< OneD, int > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 881 of file QuadExp.cpp.

References ASSERTL0, and Nektar::StdRegions::StdExpansion::m_base.

884  {
885  int nquad0 = m_base[0]->GetNumPoints();
886  int nquad1 = m_base[1]->GetNumPoints();
887 
888  // Get points in Cartesian orientation
889  switch (edge)
890  {
891  case 0:
892  outarray = Array<OneD, int>(nquad0);
893  for (int i = 0; i < nquad0; ++i)
894  {
895  outarray[i] = i;
896  }
897  break;
898  case 1:
899  outarray = Array<OneD, int>(nquad1);
900  for (int i = 0; i < nquad1; ++i)
901  {
902  outarray[i] = (nquad0-1) + i*nquad0;
903  }
904  break;
905  case 2:
906  outarray = Array<OneD, int>(nquad0);
907  for (int i = 0; i < nquad0; ++i)
908  {
909  outarray[i] = i + nquad0*(nquad1-1);
910  }
911  break;
912  case 3:
913  outarray = Array<OneD, int>(nquad1);
914  for (int i = 0; i < nquad1; ++i)
915  {
916  outarray[i] = i + i*(nquad0-1);
917  }
918  break;
919  default:
920  ASSERTL0(false, "edge value (< 3) is out of range");
921  break;
922  }
923 
924  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
void Nektar::LocalRegions::QuadExp::v_GetEdgePhysVals ( const int  edge,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Extract the physical values along edge edge from inarray into outarray following the local edge orientation and point distribution defined by defined in EdgeExp.

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 675 of file QuadExp.cpp.

References ASSERTL0, Nektar::StdRegions::eForwards, Nektar::StdRegions::StdExpansion::GetEorient(), Nektar::StdRegions::StdExpansion::m_base, and Vmath::Vcopy().

Referenced by v_GetTracePhysVals().

679  {
680  int nquad0 = m_base[0]->GetNumPoints();
681  int nquad1 = m_base[1]->GetNumPoints();
682 
683  StdRegions::Orientation edgedir = GetEorient(edge);
684  switch(edge)
685  {
686  case 0:
687  if (edgedir == StdRegions::eForwards)
688  {
689  Vmath::Vcopy(nquad0,&(inarray[0]),1,&(outarray[0]),1);
690  }
691  else
692  {
693  Vmath::Vcopy(nquad0,&(inarray[0])+(nquad0-1),-1,
694  &(outarray[0]),1);
695  }
696  break;
697  case 1:
698  if (edgedir == StdRegions::eForwards)
699  {
700  Vmath::Vcopy(nquad1,&(inarray[0])+(nquad0-1),nquad0,
701  &(outarray[0]),1);
702  }
703  else
704  {
705  Vmath::Vcopy(nquad1,&(inarray[0])+(nquad0*nquad1-1),
706  -nquad0, &(outarray[0]),1);
707  }
708  break;
709  case 2:
710  if (edgedir == StdRegions::eForwards)
711  {
712  Vmath::Vcopy(nquad0,&(inarray[0])+(nquad0*nquad1-1),-1,
713  &(outarray[0]),1);
714  }
715  else
716  {
717  Vmath::Vcopy(nquad0,&(inarray[0])+nquad0*(nquad1-1),1,
718  &(outarray[0]),1);
719  }
720  break;
721  case 3:
722  if (edgedir == StdRegions::eForwards)
723  {
724  Vmath::Vcopy(nquad1,&(inarray[0]) + nquad0*(nquad1-1),
725  -nquad0,&(outarray[0]),1);
726  }
727  else
728  {
729  Vmath::Vcopy(nquad1,&(inarray[0]),nquad0,
730  &(outarray[0]),1);
731  }
732  break;
733  default:
734  ASSERTL0(false,"edge value (< 3) is out of range");
735  break;
736  }
737  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::StdRegions::StdExpansion::GetEorient
StdRegions::Orientation GetEorient(int edge)
Definition: StdExpansion.h:762
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
void Nektar::LocalRegions::QuadExp::v_GetEdgePhysVals ( const int  edge,
const StdRegions::StdExpansionSharedPtr &  EdgeExp,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Definition at line 751 of file QuadExp.cpp.

References ASSERTL0, Nektar::StdRegions::eBackwards, Nektar::LibUtilities::eGaussGaussLegendre, Nektar::StdRegions::StdExpansion::GetCartesianEorient(), Nektar::StdRegions::StdExpansion::GetPointsType(), Nektar::LibUtilities::Interp1D(), Nektar::StdRegions::StdExpansion::m_base, Vmath::Reverse(), v_GetEdgeInterpVals(), and Vmath::Vcopy().

756  {
757  int nquad0 = m_base[0]->GetNumPoints();
758  int nquad1 = m_base[1]->GetNumPoints();
759 
760  // Implementation for all the basis except Gauss points
761  if (m_base[0]->GetPointsType() !=
762  LibUtilities::eGaussGaussLegendre &&
763  m_base[1]->GetPointsType() !=
764  LibUtilities::eGaussGaussLegendre)
765  {
766  // get points in Cartesian orientation
767  switch (edge)
768  {
769  case 0:
770  Vmath::Vcopy(nquad0,&(inarray[0]),1,&(outarray[0]),1);
771  break;
772  case 1:
773  Vmath::Vcopy(nquad1,&(inarray[0])+(nquad0-1),
774  nquad0,&(outarray[0]),1);
775  break;
776  case 2:
777  Vmath::Vcopy(nquad0,&(inarray[0])+nquad0*(nquad1-1),1,
778  &(outarray[0]),1);
779  break;
780  case 3:
781  Vmath::Vcopy(nquad1,&(inarray[0]),nquad0,
782  &(outarray[0]),1);
783  break;
784  default:
785  ASSERTL0(false,"edge value (< 3) is out of range");
786  break;
787  }
788  }
789  else
790  {
791  QuadExp::v_GetEdgeInterpVals(edge, inarray, outarray);
792  }
793 
794  // Interpolate if required
795  if (m_base[edge%2]->GetPointsKey() !=
796  EdgeExp->GetBasis(0)->GetPointsKey())
797  {
798  Array<OneD,NekDouble> outtmp(max(nquad0,nquad1));
799 
800  outtmp = outarray;
801 
802  LibUtilities::Interp1D(
803  m_base[edge%2]->GetPointsKey(), outtmp,
804  EdgeExp->GetBasis(0)->GetPointsKey(), outarray);
805  }
806 
807  //Reverse data if necessary
808  if(GetCartesianEorient(edge) == StdRegions::eBackwards)
809  {
810  Vmath::Reverse(EdgeExp->GetNumPoints(0),&outarray[0], 1,
811  &outarray[0], 1);
812  }
813  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::StdRegions::StdExpansion::GetCartesianEorient
StdRegions::Orientation GetCartesianEorient(int edge)
Definition: StdExpansion.h:772
Nektar::LocalRegions::QuadExp::v_GetEdgeInterpVals
virtual void v_GetEdgeInterpVals(const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: QuadExp.cpp:815
Nektar::LibUtilities::eGaussGaussLegendre
1D Gauss-Gauss-Legendre quadrature points
Definition: PointsType.h:47
Vmath::Reverse
void Reverse(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1071
Nektar::LibUtilities::Interp1D
void Interp1D(const BasisKey &fbasis0, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, Array< OneD, NekDouble > &to)
this function interpolates a 1D function evaluated at the quadrature points of the basis fbasis0 to ...
Definition: Interp.cpp:54
Nektar::StdRegions::StdExpansion::GetPointsType
LibUtilities::PointsType GetPointsType(const int dir) const
This function returns the type of quadrature points used in the dir direction.
Definition: StdExpansion.h:216
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
void Nektar::LocalRegions::QuadExp::v_GetEdgeQFactors ( const int  edge,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 929 of file QuadExp.cpp.

References ASSERTL0, Nektar::SpatialDomains::eDeformed, Nektar::LibUtilities::eGaussGaussLegendre, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetPointsType(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Reverse(), v_GetEdgeInterpVals(), Vmath::Vcopy(), and Vmath::Vmul().

932  {
933  int i;
934  int nquad0 = m_base[0]->GetNumPoints();
935  int nquad1 = m_base[1]->GetNumPoints();
936 
937  LibUtilities::PointsKeyVector ptsKeys = GetPointsKeys();
938  const Array<OneD, const NekDouble>& jac = m_metricinfo->GetJac(ptsKeys);
939  const Array<TwoD, const NekDouble>& df = m_metricinfo->GetDerivFactors(ptsKeys);
940 
941  Array<OneD, NekDouble> j (max(nquad0, nquad1), 0.0);
942  Array<OneD, NekDouble> g0(max(nquad0, nquad1), 0.0);
943  Array<OneD, NekDouble> g1(max(nquad0, nquad1), 0.0);
944  Array<OneD, NekDouble> g2(max(nquad0, nquad1), 0.0);
945  Array<OneD, NekDouble> g3(max(nquad0, nquad1), 0.0);
946 
947  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
948  {
949  // Implementation for all the basis except Gauss points
950  if (m_base[0]->GetPointsType()
951  != LibUtilities::eGaussGaussLegendre
952  && m_base[1]->GetPointsType() !=
953  LibUtilities::eGaussGaussLegendre)
954  {
955  switch (edge)
956  {
957  case 0:
958  Vmath::Vcopy(nquad0, &(df[1][0]),
959  1, &(g1[0]), 1);
960  Vmath::Vcopy(nquad0, &(df[3][0]),
961  1, &(g3[0]), 1);
962  Vmath::Vcopy(nquad0, &(jac[0]),1, &(j[0]), 1);
963 
964  for (i = 0; i < nquad0; ++i)
965  {
966  outarray[i] = j[i]*sqrt(g1[i]*g1[i]
967  + g3[i]*g3[i]);
968  }
969  break;
970  case 1:
971  Vmath::Vcopy(nquad1,
972  &(df[0][0])+(nquad0-1), nquad0,
973  &(g0[0]), 1);
974 
975  Vmath::Vcopy(nquad1,
976  &(df[2][0])+(nquad0-1), nquad0,
977  &(g2[0]), 1);
978 
979  Vmath::Vcopy(nquad1,
980  &(jac[0])+(nquad0-1), nquad0,
981  &(j[0]), 1);
982 
983  for (i = 0; i < nquad1; ++i)
984  {
985  outarray[i] = j[i]*sqrt(g0[i]*g0[i] +
986  g2[i]*g2[i]);
987  }
988  break;
989  case 2:
990 
991  Vmath::Vcopy(nquad0,
992  &(df[1][0])+(nquad0*nquad1-1), -1,
993  &(g1[0]), 1);
994 
995  Vmath::Vcopy(nquad0,
996  &(df[3][0])+(nquad0*nquad1-1), -1,
997  &(g3[0]), 1);
998 
999  Vmath::Vcopy(nquad0,
1000  &(jac[0])+(nquad0*nquad1-1), -1,
1001  &(j[0]), 1);
1002 
1003  for (i = 0; i < nquad0; ++i)
1004  {
1005  outarray[i] = j[i]*sqrt(g1[i]*g1[i]
1006  + g3[i]*g3[i]);
1007  }
1008  break;
1009  case 3:
1010 
1011  Vmath::Vcopy(nquad1,
1012  &(df[0][0])+nquad0*(nquad1-1),
1013  -nquad0,&(g0[0]), 1);
1014 
1015  Vmath::Vcopy(nquad1,
1016  &(df[2][0])+nquad0*(nquad1-1),
1017  -nquad0,&(g2[0]), 1);
1018 
1019  Vmath::Vcopy(nquad1,
1020  &(jac[0])+nquad0*(nquad1-1), -nquad0,
1021  &(j[0]), 1);
1022 
1023  for (i = 0; i < nquad1; ++i)
1024  {
1025  outarray[i] = j[i]*sqrt(g0[i]*g0[i] +
1026  g2[i]*g2[i]);
1027  }
1028  break;
1029  default:
1030  ASSERTL0(false,"edge value (< 3) is out of range");
1031  break;
1032  }
1033  }
1034  else
1035  {
1036  int nqtot = nquad0 * nquad1;
1037  Array<OneD, NekDouble> tmp_gmat0(nqtot, 0.0);
1038  Array<OneD, NekDouble> tmp_gmat1(nqtot, 0.0);
1039  Array<OneD, NekDouble> tmp_gmat2(nqtot, 0.0);
1040  Array<OneD, NekDouble> tmp_gmat3(nqtot, 0.0);
1041  Array<OneD, NekDouble> g0_edge(max(nquad0, nquad1), 0.0);
1042  Array<OneD, NekDouble> g1_edge(max(nquad0, nquad1), 0.0);
1043  Array<OneD, NekDouble> g2_edge(max(nquad0, nquad1), 0.0);
1044  Array<OneD, NekDouble> g3_edge(max(nquad0, nquad1), 0.0);
1045  Array<OneD, NekDouble> jac_edge(max(nquad0, nquad1), 0.0);
1046 
1047  switch (edge)
1048  {
1049  case 0:
1050  Vmath::Vmul(nqtot,&(df[1][0]),1,&jac[0],1,
1051  &(tmp_gmat1[0]),1);
1052  Vmath::Vmul(nqtot,&(df[3][0]),1,&jac[0],1,
1053  &(tmp_gmat3[0]),1);
1054  QuadExp::v_GetEdgeInterpVals(
1055  edge, tmp_gmat1, g1_edge);
1056  QuadExp::v_GetEdgeInterpVals(
1057  edge, tmp_gmat3, g3_edge);
1058 
1059  for (i = 0; i < nquad0; ++i)
1060  {
1061  outarray[i] = sqrt(g1_edge[i]*g1_edge[i] +
1062  g3_edge[i]*g3_edge[i]);
1063  }
1064  break;
1065 
1066  case 1:
1067  Vmath::Vmul(nqtot,
1068  &(df[0][0]), 1,
1069  &jac[0], 1,
1070  &(tmp_gmat0[0]), 1);
1071  Vmath::Vmul(nqtot,
1072  &(df[2][0]), 1,
1073  &jac[0], 1,
1074  &(tmp_gmat2[0]),
1075  1);
1076  QuadExp::v_GetEdgeInterpVals(
1077  edge, tmp_gmat0, g0_edge);
1078  QuadExp::v_GetEdgeInterpVals(
1079  edge, tmp_gmat2, g2_edge);
1080 
1081  for (i = 0; i < nquad1; ++i)
1082  {
1083  outarray[i] = sqrt(g0_edge[i]*g0_edge[i]
1084  + g2_edge[i]*g2_edge[i]);
1085  }
1086 
1087  break;
1088  case 2:
1089 
1090  Vmath::Vmul(nqtot,
1091  &(df[1][0]), 1,
1092  &jac[0], 1,
1093  &(tmp_gmat1[0]), 1);
1094  Vmath::Vmul(nqtot,
1095  &(df[3][0]), 1,
1096  &jac[0], 1,
1097  &(tmp_gmat3[0]),1);
1098  QuadExp::v_GetEdgeInterpVals(
1099  edge, tmp_gmat1, g1_edge);
1100  QuadExp::v_GetEdgeInterpVals(
1101  edge, tmp_gmat3, g3_edge);
1102 
1103 
1104  for (i = 0; i < nquad0; ++i)
1105  {
1106  outarray[i] = sqrt(g1_edge[i]*g1_edge[i]
1107  + g3_edge[i]*g3_edge[i]);
1108  }
1109 
1110  Vmath::Reverse(nquad0,&outarray[0],1,&outarray[0],1);
1111 
1112  break;
1113  case 3:
1114  Vmath::Vmul(nqtot,
1115  &(df[0][0]), 1,
1116  &jac[0], 1,
1117  &(tmp_gmat0[0]), 1);
1118  Vmath::Vmul(nqtot,
1119  &(df[2][0]),1,
1120  &jac[0], 1,
1121  &(tmp_gmat2[0]),1);
1122  QuadExp::v_GetEdgeInterpVals(
1123  edge, tmp_gmat0, g0_edge);
1124  QuadExp::v_GetEdgeInterpVals(
1125  edge, tmp_gmat2, g2_edge);
1126 
1127 
1128  for (i = 0; i < nquad1; ++i)
1129  {
1130  outarray[i] = sqrt(g0_edge[i]*g0_edge[i] +
1131  g2_edge[i]*g2_edge[i]);
1132  }
1133 
1134  Vmath::Reverse(nquad1,
1135  &outarray[0], 1,
1136  &outarray[0], 1);
1137 
1138  break;
1139  default:
1140  ASSERTL0(false,"edge value (< 3) is out of range");
1141  break;
1142  }
1143  }
1144  }
1145  else
1146  {
1147 
1148  switch (edge)
1149  {
1150  case 0:
1151 
1152 
1153 
1154  for (i = 0; i < nquad0; ++i)
1155  {
1156  outarray[i] = jac[0]*sqrt(df[1][0]*df[1][0] +
1157  df[3][0]*df[3][0]);
1158  }
1159  break;
1160  case 1:
1161  for (i = 0; i < nquad1; ++i)
1162  {
1163  outarray[i] = jac[0]*sqrt(df[0][0]*df[0][0] +
1164  df[2][0]*df[2][0]);
1165  }
1166  break;
1167  case 2:
1168  for (i = 0; i < nquad0; ++i)
1169  {
1170  outarray[i] = jac[0]*sqrt(df[1][0]*df[1][0] +
1171  df[3][0]*df[3][0]);
1172  }
1173  break;
1174  case 3:
1175  for (i = 0; i < nquad1; ++i)
1176  {
1177  outarray[i] = jac[0]*sqrt(df[0][0]*df[0][0] +
1178  df[2][0]*df[2][0]);
1179  }
1180  break;
1181  default:
1182  ASSERTL0(false,"edge value (< 3) is out of range");
1183  break;
1184  }
1185  }
1186  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::LibUtilities::PointsKeyVector
std::vector< PointsKey > PointsKeyVector
Definition: Points.h:220
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::LocalRegions::QuadExp::v_GetEdgeInterpVals
virtual void v_GetEdgeInterpVals(const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: QuadExp.cpp:815
Nektar::LibUtilities::eGaussGaussLegendre
1D Gauss-Gauss-Legendre quadrature points
Definition: PointsType.h:47
Vmath::Reverse
void Reverse(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1071
Nektar::StdRegions::StdExpansion::GetPointsType
LibUtilities::PointsType GetPointsType(const int dir) const
This function returns the type of quadrature points used in the dir direction.
Definition: StdExpansion.h:216
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
StdRegions::Orientation Nektar::LocalRegions::QuadExp::v_GetEorient ( int  edge)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1558 of file QuadExp.cpp.

References Nektar::LocalRegions::Expansion::m_geom.

1559  {
1560  return m_geom->GetEorient(edge);
1561  }
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
DNekScalMatSharedPtr Nektar::LocalRegions::QuadExp::v_GetLocMatrix ( const MatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::LocalRegions::Expansion.

Definition at line 2058 of file QuadExp.cpp.

References m_matrixManager.

2059  {
2060  return m_matrixManager[mkey];
2061  }
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
DNekScalBlkMatSharedPtr Nektar::LocalRegions::QuadExp::v_GetLocStaticCondMatrix ( const MatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 2064 of file QuadExp.cpp.

References m_staticCondMatrixManager.

2066  {
2067  return m_staticCondMatrixManager[mkey];
2068  }
Nektar::LocalRegions::QuadExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: QuadExp.h:286
const SpatialDomains::GeomFactorsSharedPtr & Nektar::LocalRegions::QuadExp::v_GetMetricInfo ( ) const
protectedvirtual

Reimplemented from Nektar::LocalRegions::Expansion.

Definition at line 1479 of file QuadExp.cpp.

References Nektar::LocalRegions::Expansion::m_metricinfo.

1480  {
1481  return m_metricinfo;
1482  }
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
int Nektar::LocalRegions::QuadExp::v_GetNumPoints ( const int  dir) const
protectedvirtual

Definition at line 1577 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::GetNumPoints().

1578  {
1579  return GetNumPoints(dir);
1580  }
Nektar::StdRegions::StdExpansion::GetNumPoints
int GetNumPoints(const int dir) const
This function returns the number of quadrature points in the dir direction.
Definition: StdExpansion.h:229
StdRegions::StdExpansionSharedPtr Nektar::LocalRegions::QuadExp::v_GetStdExp ( void  ) const
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 612 of file QuadExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::StdRegions::StdExpansion::m_base.

613  {
614  return MemoryManager<StdRegions::StdQuadExp>
615  ::AllocateSharedPtr(m_base[0]->GetBasisKey(),
616  m_base[1]->GetBasisKey());
617  }
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
void Nektar::LocalRegions::QuadExp::v_GetTracePhysVals ( const int  edge,
const StdRegions::StdExpansionSharedPtr &  EdgeExp,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
StdRegions::Orientation  orient 
)
protectedvirtual

Definition at line 740 of file QuadExp.cpp.

References v_GetEdgePhysVals().

746  {
747  v_GetEdgePhysVals(edge,EdgeExp,inarray,outarray);
748  }
Nektar::LocalRegions::QuadExp::v_GetEdgePhysVals
virtual void v_GetEdgePhysVals(const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Extract the physical values along edge edge from inarray into outarray following the local edge orien...
Definition: QuadExp.cpp:675
void Nektar::LocalRegions::QuadExp::v_HelmholtzMatrixOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 2136 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::HelmholtzMatrixOp_MatFree().

2140  {
2141  QuadExp::HelmholtzMatrixOp_MatFree(inarray, outarray, mkey);
2142  }
Nektar::StdRegions::StdExpansion::HelmholtzMatrixOp_MatFree
void HelmholtzMatrixOp_MatFree(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
Definition: StdExpansion.h:1531
NekDouble Nektar::LocalRegions::QuadExp::v_Integral ( const Array< OneD, const NekDouble > &  inarray)
protectedvirtual

Integrates the specified function over the domain.

See also
StdRegions::StdExpansion::Integral.

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 84 of file QuadExp.cpp.

References Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Smul(), and Vmath::Vmul().

87  {
88  int nquad0 = m_base[0]->GetNumPoints();
89  int nquad1 = m_base[1]->GetNumPoints();
90  Array<OneD, const NekDouble> jac = m_metricinfo->GetJac(GetPointsKeys());
91  NekDouble ival;
92  Array<OneD,NekDouble> tmp(nquad0*nquad1);
93 
94  // multiply inarray with Jacobian
95  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
96  {
97  Vmath::Vmul(nquad0*nquad1, jac, 1, inarray, 1, tmp, 1);
98  }
99  else
100  {
101  Vmath::Smul(nquad0*nquad1, jac[0], inarray, 1, tmp, 1);
102  }
103 
104  // call StdQuadExp version;
105  ival = StdQuadExp::v_Integral(tmp);
106  return ival;
107  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::QuadExp::v_IProductWRTBase ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Calculate the inner product of inarray with respect to the basis B=base0*base1 and put into outarray.

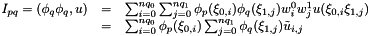
$ \begin{array}{rcl} I_{pq} = (\phi_q \phi_q, u) & = & \sum_{i=0}^{nq_0} \sum_{j=0}^{nq_1} \phi_p(\xi_{0,i}) \phi_q(\xi_{1,j}) w^0_i w^1_j u(\xi_{0,i} \xi_{1,j}) \\ & = & \sum_{i=0}^{nq_0} \phi_p(\xi_{0,i}) \sum_{j=0}^{nq_1} \phi_q(\xi_{1,j}) \tilde{u}_{i,j} \end{array} $

where

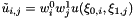
$ \tilde{u}_{i,j} = w^0_i w^1_j u(\xi_{0,i},\xi_{1,j}) $

which can be implemented as

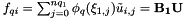
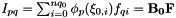
$ f_{qi} = \sum_{j=0}^{nq_1} \phi_q(\xi_{1,j}) \tilde{u}_{i,j} = {\bf B_1 U} $ $ I_{pq} = \sum_{i=0}^{nq_0} \phi_p(\xi_{0,i}) f_{qi} = {\bf B_0 F} $

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 409 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::IProductWRTBase_SumFac(), Nektar::StdRegions::StdExpansion::m_base, and Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric().

412  {
413  if (m_base[0]->Collocation() && m_base[1]->Collocation())
414  {
415  MultiplyByQuadratureMetric(inarray,outarray);
416  }
417  else
418  {
419  IProductWRTBase_SumFac(inarray,outarray);
420  }
421  }
Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric
void MultiplyByQuadratureMetric(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:942
Nektar::StdRegions::StdExpansion::IProductWRTBase_SumFac
void IProductWRTBase_SumFac(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)
Definition: StdExpansion.h:1414
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
void Nektar::LocalRegions::QuadExp::v_IProductWRTBase_MatOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 463 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eIProductWRTBase, Nektar::StdRegions::StdExpansion::GetTotPoints(), m_matrixManager, and Nektar::StdRegions::StdExpansion::m_ncoeffs.

466  {
467  int nq = GetTotPoints();
468  MatrixKey
469  iprodmatkey(StdRegions::eIProductWRTBase,DetShapeType(),*this);
470  DNekScalMatSharedPtr iprodmat = m_matrixManager[iprodmatkey];
471 
472  Blas::Dgemv('N',m_ncoeffs,nq,iprodmat->Scale(),
473  (iprodmat->GetOwnedMatrix())->GetPtr().get(),
474  m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
475 
476  }
Nektar::StdRegions::StdExpansion::DetShapeType
LibUtilities::ShapeType DetShapeType() const
This function returns the shape of the expansion domain.
Definition: StdExpansion.h:470
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::StdRegions::StdExpansion::GetTotPoints
int GetTotPoints() const
This function returns the total number of quadrature points used in the element.
Definition: StdExpansion.h:141
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
void Nektar::LocalRegions::QuadExp::v_IProductWRTBase_SumFac ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
bool  multiplybyweights = true 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 433 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::m_base, and Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric().

437  {
438  int nquad0 = m_base[0]->GetNumPoints();
439  int nquad1 = m_base[1]->GetNumPoints();
440  int order0 = m_base[0]->GetNumModes();
441 
442  if(multiplybyweights)
443  {
444  Array<OneD,NekDouble> tmp(nquad0*nquad1+nquad1*order0);
445  Array<OneD,NekDouble> wsp(tmp+nquad0*nquad1);
446 
447  MultiplyByQuadratureMetric(inarray,tmp);
448  StdQuadExp::IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
449  m_base[1]->GetBdata(),
450  tmp,outarray,wsp,true,true);
451  }
452  else
453  {
454  Array<OneD,NekDouble> wsp(nquad1*order0);
455 
456  StdQuadExp::IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
457  m_base[1]->GetBdata(),
458  inarray,outarray,wsp,true,true);
459  }
460  }
Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric
void MultiplyByQuadratureMetric(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:942
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
void Nektar::LocalRegions::QuadExp::v_IProductWRTDerivBase ( const int  dir,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 424 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::IProductWRTDerivBase_SumFac().

428  {
429  IProductWRTDerivBase_SumFac(dir,inarray,outarray);
430  }
Nektar::StdRegions::StdExpansion::IProductWRTDerivBase_SumFac
void IProductWRTDerivBase_SumFac(const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:1467
void Nektar::LocalRegions::QuadExp::v_IProductWRTDerivBase_MatOp ( const int  dir,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 535 of file QuadExp.cpp.

References ASSERTL1, Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eIProductWRTDerivBase0, Nektar::StdRegions::eIProductWRTDerivBase1, Nektar::StdRegions::eIProductWRTDerivBase2, Nektar::StdRegions::StdExpansion::GetTotPoints(), m_matrixManager, and Nektar::StdRegions::StdExpansion::m_ncoeffs.

539  {
540  int nq = GetTotPoints();
541  StdRegions::MatrixType mtype = StdRegions::eIProductWRTDerivBase0;
542 
543  switch (dir)
544  {
545  case 0:
546  {
547  mtype = StdRegions::eIProductWRTDerivBase0;
548  }
549  break;
550  case 1:
551  {
552  mtype = StdRegions::eIProductWRTDerivBase1;
553  }
554  break;
555  case 2:
556  {
557  mtype = StdRegions::eIProductWRTDerivBase2;
558  }
559  break;
560  default:
561  {
562  ASSERTL1(false,"input dir is out of range");
563  }
564  break;
565  }
566 
567  MatrixKey iprodmatkey(mtype,DetShapeType(),*this);
568  DNekScalMatSharedPtr iprodmat = m_matrixManager[iprodmatkey];
569 
570  Blas::Dgemv('N', m_ncoeffs, nq, iprodmat->Scale(),
571  (iprodmat->GetOwnedMatrix())->GetPtr().get(),
572  m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
573  }
Nektar::StdRegions::StdExpansion::DetShapeType
LibUtilities::ShapeType DetShapeType() const
This function returns the shape of the expansion domain.
Definition: StdExpansion.h:470
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::StdRegions::StdExpansion::GetTotPoints
int GetTotPoints() const
This function returns the total number of quadrature points used in the element.
Definition: StdExpansion.h:141
Nektar::LocalRegions::QuadExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: QuadExp.h:285
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
void Nektar::LocalRegions::QuadExp::v_IProductWRTDerivBase_SumFac ( const int  dir,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 479 of file QuadExp.cpp.

References ASSERTL1, Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion2D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_geom, Nektar::LocalRegions::Expansion::m_metricinfo, Nektar::StdRegions::StdExpansion::m_ncoeffs, Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric(), Vmath::Smul(), Vmath::Vadd(), and Vmath::Vmul().

483  {
484  ASSERTL1((dir==0) || (dir==1) || (dir==2),
485  "Invalid direction.");
486  ASSERTL1((dir==2) ? (m_geom->GetCoordim() ==3):true,
487  "Invalid direction.");
488 
489  int nquad0 = m_base[0]->GetNumPoints();
490  int nquad1 = m_base[1]->GetNumPoints();
491  int nqtot = nquad0*nquad1;
492  int nmodes0 = m_base[0]->GetNumModes();
493 
494  const Array<TwoD, const NekDouble>& df = m_metricinfo->GetDerivFactors(GetPointsKeys());
495 
496  Array<OneD, NekDouble> tmp1(2*nqtot+m_ncoeffs+nmodes0*nquad1);
497  Array<OneD, NekDouble> tmp2(tmp1 + nqtot);
498  Array<OneD, NekDouble> tmp3(tmp1 + 2*nqtot);
499  Array<OneD, NekDouble> tmp4(tmp1 + 2*nqtot+m_ncoeffs);
500 
501  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
502  {
503  Vmath::Vmul(nqtot,
504  &df[2*dir][0], 1,
505  inarray.get(), 1,
506  tmp1.get(), 1);
507  Vmath::Vmul(nqtot,
508  &df[2*dir+1][0], 1,
509  inarray.get(), 1,
510  tmp2.get(),1);
511  }
512  else
513  {
514  Vmath::Smul(nqtot,
515  df[2*dir][0], inarray.get(), 1,
516  tmp1.get(), 1);
517  Vmath::Smul(nqtot,
518  df[2*dir+1][0], inarray.get(), 1,
519  tmp2.get(), 1);
520  }
521 
522  MultiplyByQuadratureMetric(tmp1,tmp1);
523  MultiplyByQuadratureMetric(tmp2,tmp2);
524 
525  IProductWRTBase_SumFacKernel(
526  m_base[0]->GetDbdata(), m_base[1]->GetBdata(),
527  tmp1, tmp3, tmp4, false, true);
528  IProductWRTBase_SumFacKernel(
529  m_base[0]->GetBdata() , m_base[1]->GetDbdata(),
530  tmp2, outarray, tmp4, true, false);
531  Vmath::Vadd(m_ncoeffs, tmp3, 1, outarray, 1, outarray, 1);
532  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric
void MultiplyByQuadratureMetric(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:942
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::StdRegions::StdExpansion2D::IProductWRTBase_SumFacKernel
void IProductWRTBase_SumFacKernel(const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0=true, bool doCheckCollDir1=true)
Definition: StdExpansion2D.cpp:200
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::QuadExp::v_LaplacianMatrixOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 2085 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::LaplacianMatrixOp_MatFree().

2089  {
2090  QuadExp::LaplacianMatrixOp_MatFree(inarray, outarray, mkey);
2091  }
Nektar::StdRegions::StdExpansion::LaplacianMatrixOp_MatFree
void LaplacianMatrixOp_MatFree(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
Definition: StdExpansion.h:1489
void Nektar::LocalRegions::QuadExp::v_LaplacianMatrixOp ( const int  k1,
const int  k2,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 2094 of file QuadExp.cpp.

2100  {
2101  StdExpansion::LaplacianMatrixOp_MatFree(
2102  k1, k2, inarray, outarray, mkey);
2103  }
void Nektar::LocalRegions::QuadExp::v_LaplacianMatrixOp_MatFree_Kernel ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
Array< OneD, NekDouble > &  wsp 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 2220 of file QuadExp.cpp.

References ASSERTL1, Nektar::LocalRegions::Expansion::ComputeLaplacianMetric(), Nektar::LocalRegions::eMetricLaplacian00, Nektar::LocalRegions::eMetricLaplacian01, Nektar::LocalRegions::eMetricLaplacian11, Nektar::StdRegions::StdExpansion2D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metrics, Nektar::StdRegions::StdExpansion::m_ncoeffs, Vmath::Vadd(), and Vmath::Vvtvvtp().

2224  {
2225  if (m_metrics.count(eMetricLaplacian00) == 0)
2226  {
2227  ComputeLaplacianMetric();
2228  }
2229 
2230  int nquad0 = m_base[0]->GetNumPoints();
2231  int nquad1 = m_base[1]->GetNumPoints();
2232  int nqtot = nquad0*nquad1;
2233  int nmodes0 = m_base[0]->GetNumModes();
2234  int nmodes1 = m_base[1]->GetNumModes();
2235  int wspsize = max(max(max(nqtot,m_ncoeffs),nquad1*nmodes0),nquad0*nmodes1);
2236 
2237  ASSERTL1(wsp.num_elements() >= 3*wspsize,
2238  "Workspace is of insufficient size.");
2239 
2240  const Array<OneD, const NekDouble>& base0 = m_base[0]->GetBdata();
2241  const Array<OneD, const NekDouble>& base1 = m_base[1]->GetBdata();
2242  const Array<OneD, const NekDouble>& dbase0 = m_base[0]->GetDbdata();
2243  const Array<OneD, const NekDouble>& dbase1 = m_base[1]->GetDbdata();
2244  const Array<OneD, const NekDouble>& metric00 = m_metrics[eMetricLaplacian00];
2245  const Array<OneD, const NekDouble>& metric01 = m_metrics[eMetricLaplacian01];
2246  const Array<OneD, const NekDouble>& metric11 = m_metrics[eMetricLaplacian11];
2247 
2248  // Allocate temporary storage
2249  Array<OneD,NekDouble> wsp0(wsp);
2250  Array<OneD,NekDouble> wsp1(wsp+wspsize);
2251  Array<OneD,NekDouble> wsp2(wsp+2*wspsize);
2252 
2253  StdExpansion2D::PhysTensorDeriv(inarray,wsp1,wsp2);
2254 
2255  // wsp0 = k = g0 * wsp1 + g1 * wsp2 = g0 * du_dxi1 + g1 * du_dxi2
2256  // wsp2 = l = g1 * wsp1 + g2 * wsp2 = g0 * du_dxi1 + g1 * du_dxi2
2257  // where g0, g1 and g2 are the metric terms set up in the GeomFactors class
2258  // especially for this purpose
2259  Vmath::Vvtvvtp(nqtot,&metric00[0],1,&wsp1[0],1,&metric01[0],1,&wsp2[0],1,&wsp0[0],1);
2260  Vmath::Vvtvvtp(nqtot,&metric01[0],1,&wsp1[0],1,&metric11[0],1,&wsp2[0],1,&wsp2[0],1);
2261 
2262  // outarray = m = (D_xi1 * B)^T * k
2263  // wsp1 = n = (D_xi2 * B)^T * l
2264  IProductWRTBase_SumFacKernel(dbase0,base1,wsp0,outarray,wsp1,false,true);
2265  IProductWRTBase_SumFacKernel(base0,dbase1,wsp2,wsp1, wsp0,true,false);
2266 
2267  // outarray = outarray + wsp1
2268  // = L * u_hat
2269  Vmath::Vadd(m_ncoeffs,wsp1.get(),1,outarray.get(),1,outarray.get(),1);
2270  }
Vmath::Vvtvvtp
void Vvtvvtp(int n, const T *v, int incv, const T *w, int incw, const T *x, int incx, const T *y, int incy, T *z, int incz)
vvtvvtp (vector times vector plus vector times vector):
Definition: Vmath.cpp:523
Nektar::StdRegions::StdExpansion2D::IProductWRTBase_SumFacKernel
void IProductWRTBase_SumFacKernel(const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0=true, bool doCheckCollDir1=true)
Definition: StdExpansion2D.cpp:200
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
void Nektar::LocalRegions::QuadExp::v_MassLevelCurvatureMatrixOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 2126 of file QuadExp.cpp.

2130  {
2131  StdExpansion::MassLevelCurvatureMatrixOp_MatFree(
2132  inarray, outarray, mkey);
2133  }
void Nektar::LocalRegions::QuadExp::v_MassMatrixOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 2076 of file QuadExp.cpp.

2080  {
2081  StdExpansion::MassMatrixOp_MatFree(inarray, outarray, mkey);
2082  }
void Nektar::LocalRegions::QuadExp::v_NormVectorIProductWRTBase ( const Array< OneD, const NekDouble > &  Fx,
const Array< OneD, const NekDouble > &  Fy,
const Array< OneD, const NekDouble > &  Fz,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 576 of file QuadExp.cpp.

References Nektar::SpatialDomains::eDeformed, Nektar::LocalRegions::Expansion2D::GetLeftAdjacentElementExp(), Nektar::LocalRegions::Expansion2D::GetLeftAdjacentElementFace(), Nektar::StdRegions::StdExpansion::IProductWRTBase(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Svtsvtp(), Vmath::Svtvp(), Vmath::Vvtvp(), and Vmath::Vvtvvtp().

581  {
582  int nq = m_base[0]->GetNumPoints()*m_base[1]->GetNumPoints();
583  Array<OneD, NekDouble> Fn(nq);
584 
585  const Array<OneD, const Array<OneD, NekDouble> > &normals =
586  GetLeftAdjacentElementExp()->GetFaceNormal(
587  GetLeftAdjacentElementFace());
588 
589  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
590  {
591  Vmath::Vvtvvtp(nq,&normals[0][0],1,&Fx[0],1,
592  &normals[1][0],1,&Fy[0],1,&Fn[0],1);
593  Vmath::Vvtvp (nq,&normals[2][0],1,&Fz[0],1,&Fn[0],1,&Fn[0],1);
594  }
595  else
596  {
597  Vmath::Svtsvtp(nq,normals[0][0],&Fx[0],1,
598  normals[1][0],&Fy[0],1,&Fn[0],1);
599  Vmath::Svtvp (nq,normals[2][0],&Fz[0],1,&Fn[0],1,&Fn[0],1);
600  }
601 
602  IProductWRTBase(Fn,outarray);
603  }
Nektar::StdRegions::StdExpansion::IProductWRTBase
void IProductWRTBase(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
this function calculates the inner product of a given function f with the different modes of the expa...
Definition: StdExpansion.h:629
Vmath::Svtvp
void Svtvp(int n, const T alpha, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
svtvp (scalar times vector plus vector): z = alpha*x + y
Definition: Vmath.cpp:471
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::LocalRegions::Expansion2D::GetLeftAdjacentElementExp
Expansion3DSharedPtr GetLeftAdjacentElementExp() const
Definition: Expansion2D.h:223
Vmath::Vvtvvtp
void Vvtvvtp(int n, const T *v, int incv, const T *w, int incw, const T *x, int incx, const T *y, int incy, T *z, int incz)
vvtvvtp (vector times vector plus vector times vector):
Definition: Vmath.cpp:523
Vmath::Svtsvtp
void Svtsvtp(int n, const T alpha, const T *x, int incx, const T beta, const T *y, int incy, T *z, int incz)
vvtvvtp (scalar times vector plus scalar times vector):
Definition: Vmath.cpp:577
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
void Nektar::LocalRegions::QuadExp::v_NormVectorIProductWRTBase ( const Array< OneD, const Array< OneD, NekDouble > > &  Fvec,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 605 of file QuadExp.cpp.

References Nektar::StdRegions::StdExpansion::NormVectorIProductWRTBase().

608  {
609  NormVectorIProductWRTBase(Fvec[0], Fvec[1], Fvec[2], outarray);
610  }
Nektar::StdRegions::StdExpansion::NormVectorIProductWRTBase
void NormVectorIProductWRTBase(const Array< OneD, const NekDouble > &Fx, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:727
void Nektar::LocalRegions::QuadExp::v_PhysDeriv ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  out_d0,
Array< OneD, NekDouble > &  out_d1,
Array< OneD, NekDouble > &  out_d2 = NullNekDouble1DArray 
)
protectedvirtual

Calculate the derivative of the physical points.

For quadrilateral region can use the Tensor_Deriv function defined under StdExpansion.

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 110 of file QuadExp.cpp.

References Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Smul(), Vmath::Vmul(), and Vmath::Vvtvp().

Referenced by v_PhysDeriv().

115  {
116  int nquad0 = m_base[0]->GetNumPoints();
117  int nquad1 = m_base[1]->GetNumPoints();
118  int nqtot = nquad0*nquad1;
119  const Array<TwoD, const NekDouble>& df = m_metricinfo->GetDerivFactors(GetPointsKeys());
120  Array<OneD,NekDouble> diff0(2*nqtot);
121  Array<OneD,NekDouble> diff1(diff0+nqtot);
122 
123  StdQuadExp::v_PhysDeriv(inarray, diff0, diff1);
124 
125  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
126  {
127  if (out_d0.num_elements())
128  {
129  Vmath::Vmul (nqtot, df[0], 1, diff0, 1, out_d0, 1);
130  Vmath::Vvtvp (nqtot, df[1], 1, diff1, 1, out_d0, 1,
131  out_d0,1);
132  }
133 
134  if(out_d1.num_elements())
135  {
136  Vmath::Vmul (nqtot,df[2],1,diff0,1, out_d1, 1);
137  Vmath::Vvtvp (nqtot,df[3],1,diff1,1, out_d1, 1, out_d1,1);
138  }
139 
140  if (out_d2.num_elements())
141  {
142  Vmath::Vmul (nqtot,df[4],1,diff0,1, out_d2, 1);
143  Vmath::Vvtvp (nqtot,df[5],1,diff1,1, out_d2, 1, out_d2,1);
144  }
145  }
146  else // regular geometry
147  {
148  if (out_d0.num_elements())
149  {
150  Vmath::Smul (nqtot, df[0][0], diff0, 1, out_d0, 1);
151  Blas::Daxpy (nqtot, df[1][0], diff1, 1, out_d0, 1);
152  }
153 
154  if (out_d1.num_elements())
155  {
156  Vmath::Smul (nqtot, df[2][0], diff0, 1, out_d1, 1);
157  Blas::Daxpy (nqtot, df[3][0], diff1, 1, out_d1, 1);
158  }
159 
160  if (out_d2.num_elements())
161  {
162  Vmath::Smul (nqtot, df[4][0], diff0, 1, out_d2, 1);
163  Blas::Daxpy (nqtot, df[5][0], diff1, 1, out_d2, 1);
164  }
165  }
166  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::QuadExp::v_PhysDeriv ( const int  dir,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  out_d0 
)
protectedvirtual

Calculate the derivative of the physical points in a given direction.

See also
StdRegions::StdExpansion::PhysDeriv

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 169 of file QuadExp.cpp.

References ASSERTL1, Nektar::NullNekDouble1DArray, and v_PhysDeriv().

173  {
174  switch (dir)
175  {
176  case 0:
177  {
178  v_PhysDeriv(inarray, outarray, NullNekDouble1DArray,
179  NullNekDouble1DArray);
180  }
181  break;
182  case 1:
183  {
184  v_PhysDeriv(inarray, NullNekDouble1DArray, outarray,
185  NullNekDouble1DArray);
186  }
187  break;
188  case 2:
189  {
190  v_PhysDeriv(inarray, NullNekDouble1DArray,
191  NullNekDouble1DArray, outarray);
192  }
193  break;
194  default:
195  {
196  ASSERTL1(false,"input dir is out of range");
197  }
198  break;
199  }
200  }
Nektar::NullNekDouble1DArray
static Array< OneD, NekDouble > NullNekDouble1DArray
Definition: SharedArray.hpp:784
Nektar::LocalRegions::QuadExp::v_PhysDeriv
virtual void v_PhysDeriv(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
Calculate the derivative of the physical points.
Definition: QuadExp.cpp:110
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
void Nektar::LocalRegions::QuadExp::v_PhysDirectionalDeriv ( const Array< OneD, const NekDouble > &  inarray,
const Array< OneD, const NekDouble > &  direction,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Physical derivative along a direction vector.

See also
StdRegions::StdExpansion::PhysDirectionalDeriv

D_v = d/dx_v^s + d/dx_v^r

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 203 of file QuadExp.cpp.

References ASSERTL1, Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_geom, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Vmul(), and Vmath::Vvtvp().

207  {
208  int nquad0 = m_base[0]->GetNumPoints();
209  int nquad1 = m_base[1]->GetNumPoints();
210  int nqtot = nquad0*nquad1;
211 
212  const Array<TwoD, const NekDouble>& df = m_metricinfo->GetDerivFactors(GetPointsKeys());
213 
214  Array<OneD,NekDouble> diff0(2*nqtot);
215  Array<OneD,NekDouble> diff1(diff0+nqtot);
216 
217  StdQuadExp::v_PhysDeriv(inarray, diff0, diff1);
218 
219  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
220  {
221  Array<OneD, Array<OneD, NekDouble> > tangmat(2);
222 
223  // d/dx_v^s = v_x*ds/dx + v_y*ds/dy + v_z*dx/dz
224  for (int i=0; i< 2; ++i)
225  {
226  tangmat[i] = Array<OneD, NekDouble>(nqtot,0.0);
227  for (int k=0; k<(m_geom->GetCoordim()); ++k)
228  {
229  Vmath::Vvtvp(nqtot,
230  &df[2*k+i][0], 1,
231  &direction[k*nqtot], 1,
232  &tangmat[i][0], 1,
233  &tangmat[i][0], 1);
234  }
235  }
236 
237  /// D_v = d/dx_v^s + d/dx_v^r
238  if (out.num_elements())
239  {
240  Vmath::Vmul (nqtot,
241  &tangmat[0][0], 1,
242  &diff0[0], 1,
243  &out[0], 1);
244  Vmath::Vvtvp (nqtot,
245  &tangmat[1][0], 1,
246  &diff1[0], 1,
247  &out[0], 1,
248  &out[0], 1);
249  }
250 
251  }
252  else
253  {
254  ASSERTL1(m_metricinfo->GetGtype() ==
255  SpatialDomains::eDeformed,"Wrong route");
256  }
257  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
NekDouble Nektar::LocalRegions::QuadExp::v_PhysEvaluate ( const Array< OneD, const NekDouble > &  coords,
const Array< OneD, const NekDouble > &  physvals 
)
protectedvirtual

This function evaluates the expansion at a single (arbitrary) point of the domain.

This function is a wrapper around the virtual function v_PhysEvaluate()

Based on the value of the expansion at the quadrature points, this function calculates the value of the expansion at an arbitrary single points (with coordinates 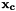$ \mathbf{x_c}$ given by the pointer coords). This operation, equivalent to

\[ u(\mathbf{x_c}) = \sum_p \phi_p(\mathbf{x_c}) \hat{u}_p \]

is evaluated using Lagrangian interpolants through the quadrature points:

\[ u(\mathbf{x_c}) = \sum_p h_p(\mathbf{x_c}) u_p\]

This function requires that the physical value array 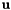$\mathbf{u}$ (implemented as the attribute #m_phys) is set.

Parameters
coordsthe coordinates of the single point
Returns
returns the value of the expansion at the single point

Reimplemented from Nektar::StdRegions::StdExpansion2D.

Definition at line 659 of file QuadExp.cpp.

References ASSERTL0, and Nektar::LocalRegions::Expansion::m_geom.

662  {
663  Array<OneD,NekDouble> Lcoord = Array<OneD, NekDouble>(2);
664 
665  ASSERTL0(m_geom,"m_geom not defined");
666  m_geom->GetLocCoords(coord,Lcoord);
667 
668  return StdQuadExp::v_PhysEvaluate(Lcoord, physvals);
669  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
void Nektar::LocalRegions::QuadExp::v_ReduceOrderCoeffs ( int  numMin,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 2170 of file QuadExp.cpp.

References Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::eOrtho_A, Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::LibUtilities::InterpCoeff2D(), Nektar::StdRegions::StdExpansion::m_base, Vmath::Vcopy(), and Vmath::Zero().

2174  {
2175  int n_coeffs = inarray.num_elements();
2176 
2177  Array<OneD, NekDouble> coeff (n_coeffs);
2178  Array<OneD, NekDouble> coeff_tmp(n_coeffs, 0.0);
2179  Array<OneD, NekDouble> tmp, tmp2;
2180 
2181  int nmodes0 = m_base[0]->GetNumModes();
2182  int nmodes1 = m_base[1]->GetNumModes();
2183  int numMax = nmodes0;
2184 
2185  Vmath::Vcopy(n_coeffs,inarray,1,coeff_tmp,1);
2186 
2187  const LibUtilities::PointsKey Pkey0(
2188  nmodes0, LibUtilities::eGaussLobattoLegendre);
2189  const LibUtilities::PointsKey Pkey1(
2190  nmodes1, LibUtilities::eGaussLobattoLegendre);
2191  LibUtilities::BasisKey b0(
2192  m_base[0]->GetBasisType(), nmodes0, Pkey0);
2193  LibUtilities::BasisKey b1(
2194  m_base[1]->GetBasisType(), nmodes1, Pkey1);
2195  LibUtilities::BasisKey bortho0(
2196  LibUtilities::eOrtho_A, nmodes0, Pkey0);
2197  LibUtilities::BasisKey bortho1(
2198  LibUtilities::eOrtho_A, nmodes1, Pkey1);
2199 
2200  LibUtilities::InterpCoeff2D(
2201  b0, b1, coeff_tmp, bortho0, bortho1, coeff);
2202 
2203  Vmath::Zero(n_coeffs, coeff_tmp, 1);
2204 
2205  int cnt = 0;
2206  for (int i = 0; i < numMin+1; ++i)
2207  {
2208  Vmath::Vcopy(numMin,
2209  tmp = coeff+cnt,1,
2210  tmp2 = coeff_tmp+cnt,1);
2211 
2212  cnt = i*numMax;
2213  }
2214 
2215  LibUtilities::InterpCoeff2D(
2216  bortho0, bortho1, coeff_tmp,
2217  b0, b1, outarray);
2218  }
Nektar::LibUtilities::eOrtho_A
Principle Orthogonal Functions .
Definition: BasisType.h:46
Nektar::StdRegions::StdExpansion::GetBasisType
LibUtilities::BasisType GetBasisType(const int dir) const
This function returns the type of basis used in the dir direction.
Definition: StdExpansion.h:165
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1422
Nektar::LibUtilities::InterpCoeff2D
void InterpCoeff2D(const BasisKey &fbasis0, const BasisKey &fbasis1, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, Array< OneD, NekDouble > &to)
Definition: InterpCoeff.cpp:73
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Nektar::LibUtilities::eGaussLobattoLegendre
1D Gauss-Lobatto-Legendre quadrature points
Definition: PointsType.h:50
NekDouble Nektar::LocalRegions::QuadExp::v_StdPhysEvaluate ( const Array< OneD, const NekDouble > &  Lcoord,
const Array< OneD, const NekDouble > &  physvals 
)
protectedvirtual

Given the local cartesian coordinate Lcoord evaluate the value of physvals at this point by calling through to the StdExpansion method

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 651 of file QuadExp.cpp.

654  {
655  // Evaluate point in local (eta) coordinates.
656  return StdQuadExp::v_PhysEvaluate(Lcoord,physvals);
657  }
void Nektar::LocalRegions::QuadExp::v_SVVLaplacianFilter ( Array< OneD, NekDouble > &  array,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 2311 of file QuadExp.cpp.

References Nektar::SpatialDomains::eDeformed, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetTotPoints(), Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Vdiv(), Vmath::Vmul(), and Vmath::Vsqrt().

2314  {
2315  int nq = GetTotPoints();
2316 
2317  // Calculate sqrt of the Jacobian
2318  Array<OneD, const NekDouble> jac =
2319  m_metricinfo->GetJac(GetPointsKeys());
2320  Array<OneD, NekDouble> sqrt_jac(nq);
2321  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
2322  {
2323  Vmath::Vsqrt(nq,jac,1,sqrt_jac,1);
2324  }
2325  else
2326  {
2327  Vmath::Fill(nq,sqrt(jac[0]),sqrt_jac,1);
2328  }
2329 
2330  // Multiply array by sqrt(Jac)
2331  Vmath::Vmul(nq,sqrt_jac,1,array,1,array,1);
2332 
2333  // Apply std region filter
2334  StdQuadExp::v_SVVLaplacianFilter( array, mkey);
2335 
2336  // Divide by sqrt(Jac)
2337  Vmath::Vdiv(nq,array,1,sqrt_jac,1,array,1);
2338  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1328
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Nektar::StdRegions::StdExpansion::GetTotPoints
int GetTotPoints() const
This function returns the total number of quadrature points used in the element.
Definition: StdExpansion.h:141
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::QuadExp::v_WeakDerivMatrixOp ( const int  i,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdQuadExp.

Definition at line 2106 of file QuadExp.cpp.

2111  {
2112  StdExpansion::WeakDerivMatrixOp_MatFree(i, inarray, outarray, mkey);
2113  }
void Nektar::LocalRegions::QuadExp::v_WeakDirectionalDerivMatrixOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 2116 of file QuadExp.cpp.

2120  {
2121  StdExpansion::WeakDirectionalDerivMatrixOp_MatFree(
2122  inarray, outarray, mkey);
2123  }

Member Data Documentation

LibUtilities::NekManager<MatrixKey, DNekScalMat, MatrixKey::opLess> Nektar::LocalRegions::QuadExp::m_matrixManager
private

Definition at line 285 of file QuadExp.h.

Referenced by CreateMatrix(), v_FwdTrans(), v_GetEdgeInterpVals(), v_GetLocMatrix(), v_IProductWRTBase_MatOp(), and v_IProductWRTDerivBase_MatOp().

LibUtilities::NekManager<MatrixKey, DNekScalBlkMat, MatrixKey::opLess> Nektar::LocalRegions::QuadExp::m_staticCondMatrixManager
private

Definition at line 286 of file QuadExp.h.

Referenced by v_DropLocStaticCondMatrix(), v_FwdTrans_BndConstrained(), and v_GetLocStaticCondMatrix().

Generated on Wed May 4 2016 17:54:30 for Nektar++ by   doxygen 1.8.8