|
Nektar++
|
|
Nektar++
|
The namespace associated with the the Polylib library (Polylib introduction) More...
Functions | |
| static void | Jacobz (const int n, double *z, const double alpha, const double beta) |
| Calculate the n zeros, z, of the Jacobi polynomial, i.e. More... | |
| static void | TriQL (const int n, double *d, double *e, double **z) |
| QL algorithm for symmetric tridiagonal matrix. More... | |
| double | gammaF (const double x) |
Calculate the Gamma function , 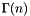 , for integer. More... , for integer. More... | |
| static void | RecCoeff (const int n, double *a, double *b, const double alpha, const double beta) |
| The routine finds the recurrence coefficients a and. More... | |
| void | JKMatrix (int n, double *a, double *b) |
| Calcualtes the Jacobi-kronrod matrix by determining the. More... | |
| void | chri1 (int n, double *a, double *b, double *a0, double *b0, double z) |
Given a weight function 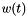 through the first n+1. More... through the first n+1. More... | |
| void | zwgj (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Jacobi zeros and weights. More... | |
| void | zwgrjm (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Radau-Jacobi zeros and weights with end point at z=-1. More... | |
| void | zwgrjp (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Radau-Jacobi zeros and weights with end point at z=1. More... | |
| void | zwglj (double *z, double *w, const int np, const double alpha, const double beta) |
| Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1. More... | |
| void | zwgk (double *z, double *w, const int npt, const double alpha, const double beta) |
| Gauss-Kronrod-Jacobi zeros and weights. More... | |
| void | zwrk (double *z, double *w, const int npt, const double alpha, const double beta) |
| Gauss-Radau-Kronrod-Jacobi zeros and weights. More... | |
| void | zwlk (double *z, double *w, const int npt, const double alpha, const double beta) |
| Gauss-Lobatto-Kronrod-Jacobi zeros and weights. More... | |
| void | Dgj (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix and its transpose associated. More... | |
| void | Dgrjm (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix and its transpose associated. More... | |
| void | Dgrjp (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix associated with the. More... | |
| void | Dglj (double *D, const double *z, const int np, const double alpha, const double beta) |
| Compute the Derivative Matrix associated with the. More... | |
| double | hgj (const int i, const double z, const double *zgj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through. More... | |
| double | hgrjm (const int i, const double z, const double *zgrj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through the. More... | |
| double | hgrjp (const int i, const double z, const double *zgrj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through the. More... | |
| double | hglj (const int i, const double z, const double *zglj, const int np, const double alpha, const double beta) |
| Compute the value of the i th Lagrangian interpolant through the. More... | |
| void | Imgj (double *im, const double *zgj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Jacobi points to an. More... | |
| void | Imgrjm (double *im, const double *zgrj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Radau-Jacobi points. More... | |
| void | Imgrjp (double *im, const double *zgrj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Radau-Jacobi points. More... | |
| void | Imglj (double *im, const double *zglj, const double *zm, const int nz, const int mz, const double alpha, const double beta) |
| Interpolation Operator from Gauss-Lobatto-Jacobi points. More... | |
| void | jacobfd (const int np, const double *z, double *poly_in, double *polyd, const int n, const double alpha, const double beta) |
Routine to calculate Jacobi polynomials, 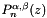 , and their first derivative, , and their first derivative, 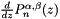 . More... . More... | |
| void | jacobd (const int np, const double *z, double *polyd, const int n, const double alpha, const double beta) |
| Calculate the derivative of Jacobi polynomials. More... | |
| void | JacZeros (const int n, double *a, double *b, const double alpha, const double beta) |
| Zero and Weight determination through the eigenvalues and eigenvectors of a tridiagonal. More... | |
| std::complex< Nektar::NekDouble > | ImagBesselComp (int n, std::complex< Nektar::NekDouble > y) |
| Calcualte the bessel function of the first kind with complex double input y. Taken from Numerical Recipies in C. More... | |
The namespace associated with the the Polylib library (Polylib introduction)
| void Polylib::chri1 | ( | int | n, |
| double * | a, | ||
| double * | b, | ||
| double * | a0, | ||
| double * | b0, | ||
| double | z | ||
| ) |
Given a weight function 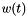 through the first n+1.
through the first n+1.
coefficients a and b of its orthogonal polynomials
this routine generates the first n recurrence coefficients for the orthogonal
polynomials relative to the modified weight function 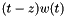 .
.
The result will be placed in the array a0 and b0.
Definition at line 2931 of file Polylib.cpp.
Referenced by zwlk(), and zwrk().
| void Polylib::Dgj | ( | double * | D, |
| const double * | z, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the Derivative Matrix and its transpose associated.
with the Gauss-Jacobi zeros.
associated with the n_th order Lagrangian interpolants through the
np Gauss-Jacobi points z such that
![$ \frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j]) $](form_116.png)
Definition at line 937 of file Polylib.cpp.
References jacobd().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateDerivMatrix(), and main().
| void Polylib::Dglj | ( | double * | D, |
| const double * | z, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the Derivative Matrix associated with the.
Gauss-Lobatto-Jacobi zeros.
order Lagrange interpolants through the np
Gauss-Lobatto-Jacobi points z such that
![$ \frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j]) $](form_116.png)
Definition at line 1221 of file Polylib.cpp.
References gammaF(), and jacobd().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateDerivMatrix(), and main().
| void Polylib::Dgrjm | ( | double * | D, |
| const double * | z, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the Derivative Matrix and its transpose associated.
with the Gauss-Radau-Jacobi zeros with a zero at z=-1.
order Lagrangian interpolants through the np Gauss-Radau-Jacobi
points z such that
![$ \frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j]) $](form_116.png)
Definition at line 1023 of file Polylib.cpp.
References gammaF(), and jacobd().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateDerivMatrix(), and main().
| void Polylib::Dgrjp | ( | double * | D, |
| const double * | z, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the Derivative Matrix associated with the.
Gauss-Radau-Jacobi zeros with a zero at z=1.
order Lagrangian interpolants through the np Gauss-Radau-Jacobi
points z such that
![$ \frac{du}{dz}(z[i]) = \sum_{j=0}^{np-1} D[i*np+j] u(z[j]) $](form_116.png)
Definition at line 1121 of file Polylib.cpp.
References gammaF(), and jacobd().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateDerivMatrix(), and main().
| double Polylib::gammaF | ( | const double | x | ) |
Calculate the Gamma function , 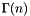 , for integer.
, for integer.
values and halves.
Determine the value of 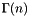 using:
using:
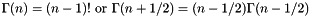
where 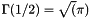
Definition at line 2205 of file Polylib.cpp.
Referenced by Dglj(), Dgrjm(), Dgrjp(), RecCoeff(), zwgj(), zwglj(), zwgrjm(), and zwgrjp().
| double Polylib::hgj | ( | const int | i, |
| const double | z, | ||
| const double * | zgj, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the value of the i th Lagrangian interpolant through.
the np Gauss-Jacobi points zgj at the arbitrary location z.
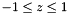
![$ \begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{P_{np}^{\alpha,\beta}(z)} {[P_{np}^{\alpha,\beta}(z_j)]^\prime (z-z_j)} & \mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array} $](form_118.png)
Definition at line 1345 of file Polylib.cpp.
References EPS, jacobd(), jacobfd(), and CellMLToNektar.cellml_metadata::p.
Referenced by Nektar::LibUtilities::Basis::GenBasis(), and Imgj().
| double Polylib::hglj | ( | const int | i, |
| const double | z, | ||
| const double * | zglj, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the value of the i th Lagrangian interpolant through the.
np Gauss-Lobatto-Jacobi points zgrj at the arbitrary location
z.
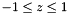
![$ \begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{(1-z^2) P_{np-2}^{\alpha+1,\beta+1}(z)} {((1-z^2_j) [P_{np-2}^{\alpha+1,\beta+1}(z_j)]^\prime - 2 z_j P_{np-2}^{\alpha+1,\beta+1}(z_j) ) (z-z_j)}&\mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array} $](form_121.png)
Definition at line 1589 of file Polylib.cpp.
References EPS, jacobd(), jacobfd(), and CellMLToNektar.cellml_metadata::p.
Referenced by Nektar::LibUtilities::Basis::GenBasis(), and Imglj().
| double Polylib::hgrjm | ( | const int | i, |
| const double | z, | ||
| const double * | zgrj, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the value of the i th Lagrangian interpolant through the.
np Gauss-Radau-Jacobi points zgrj at the arbitrary location
z. This routine assumes zgrj includes the point -1.
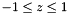
![$ \begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{(1+z) P_{np-1}^{\alpha,\beta+1}(z)} {((1+z_j) [P_{np-1}^{\alpha,\beta+1}(z_j)]^\prime + P_{np-1}^{\alpha,\beta+1}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array} $](form_119.png)
Definition at line 1421 of file Polylib.cpp.
References EPS, jacobd(), jacobfd(), and CellMLToNektar.cellml_metadata::p.
Referenced by Imgrjm().
| double Polylib::hgrjp | ( | const int | i, |
| const double | z, | ||
| const double * | zgrj, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Compute the value of the i th Lagrangian interpolant through the.
np Gauss-Radau-Jacobi points zgrj at the arbitrary location
z. This routine assumes zgrj includes the point +1.
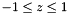
![$ \begin{array}{rcl} h_j(z) = \left\{ \begin{array}{ll} \displaystyle \frac{(1-z) P_{np-1}^{\alpha+1,\beta}(z)} {((1-z_j) [P_{np-1}^{\alpha+1,\beta}(z_j)]^\prime - P_{np-1}^{\alpha+1,\beta}(z_j) ) (z-z_j)} & \mbox{if $z \ne z_j$}\\ & \\ 1 & \mbox{if $z=z_j$} \end{array} \right. \end{array} $](form_120.png)
Definition at line 1505 of file Polylib.cpp.
References EPS, jacobd(), jacobfd(), and CellMLToNektar.cellml_metadata::p.
Referenced by Imgrjp().
| std::complex< Nektar::NekDouble > Polylib::ImagBesselComp | ( | int | n, |
| std::complex< Nektar::NekDouble > | y | ||
| ) |
Calcualte the bessel function of the first kind with complex double input y. Taken from Numerical Recipies in C.
Returns a complex double
Definition at line 2999 of file Polylib.cpp.
Referenced by Nektar::IncNavierStokes::SetWomersleyBoundary().
| void Polylib::Imgj | ( | double * | im, |
| const double * | zgj, | ||
| const double * | zm, | ||
| const int | nz, | ||
| const int | mz, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Interpolation Operator from Gauss-Jacobi points to an.
arbitrary distribution at points zm
interpolate a function from at Gauss-Jacobi distribution of nz
zeros zgrj to an arbitrary distribution of mz points zm, i.e.
![$ u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zgj[j]) $](form_122.png)
Definition at line 1657 of file Polylib.cpp.
References hgj().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateInterpMatrix(), and main().
| void Polylib::Imglj | ( | double * | im, |
| const double * | zglj, | ||
| const double * | zm, | ||
| const int | nz, | ||
| const int | mz, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Interpolation Operator from Gauss-Lobatto-Jacobi points.
to an arbitrary distrubtion at points zm
interpolate a function from at Gauss-Lobatto-Jacobi distribution of
nz zeros zgrj (where zgrj[0]=-1) to an arbitrary
distribution of mz points zm, i.e.
![$ u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zgj[j]) $](form_122.png)
Definition at line 1837 of file Polylib.cpp.
References hglj().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateInterpMatrix(), and main().
| void Polylib::Imgrjm | ( | double * | im, |
| const double * | zgrj, | ||
| const double * | zm, | ||
| const int | nz, | ||
| const int | mz, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Interpolation Operator from Gauss-Radau-Jacobi points.
(including z=-1) to an arbitrary distrubtion at points zm
interpolate a function from at Gauss-Radau-Jacobi distribution of
nz zeros zgrj (where zgrj[0]=-1) to an arbitrary
distribution of mz points zm, i.e.
![$ u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zgj[j]) $](form_122.png)
Definition at line 1715 of file Polylib.cpp.
References hgrjm().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateInterpMatrix(), and main().
| void Polylib::Imgrjp | ( | double * | im, |
| const double * | zgrj, | ||
| const double * | zm, | ||
| const int | nz, | ||
| const int | mz, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Interpolation Operator from Gauss-Radau-Jacobi points.
(including z=1) to an arbitrary distrubtion at points zm
interpolate a function from at Gauss-Radau-Jacobi distribution of
nz zeros zgrj (where zgrj[nz-1]=1) to an arbitrary
distribution of mz points zm, i.e.
![$ u(zm[i]) = \sum_{j=0}^{nz-1} im[i*nz+j] \ u(zgj[j]) $](form_122.png)
Definition at line 1775 of file Polylib.cpp.
References hgrjp().
Referenced by Nektar::LibUtilities::GaussPoints::CalculateInterpMatrix(), and main().
| void Polylib::jacobd | ( | const int | np, |
| const double * | z, | ||
| double * | polyd, | ||
| const int | n, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Calculate the derivative of Jacobi polynomials.
n th order Jacobi polynomial 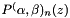 at the
at the
np points z.
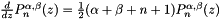
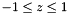
Definition at line 2151 of file Polylib.cpp.
References jacobfd().
Referenced by Dgj(), Dglj(), Dgrjm(), Dgrjp(), hgj(), hglj(), hgrjm(), hgrjp(), Nektar::LibUtilities::NodalUtilTriangle::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilTetrahedron::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilPrism::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilQuad::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilHex::v_OrthoBasisDeriv(), Nektar::SolverUtils::AdvectionFR::v_SetupCFunctions(), Nektar::SolverUtils::DiffusionLFR::v_SetupCFunctions(), Nektar::SolverUtils::DiffusionLFRNS::v_SetupCFunctions(), and zwgj().
| void Polylib::jacobfd | ( | const int | np, |
| const double * | z, | ||
| double * | poly_in, | ||
| double * | polyd, | ||
| const int | n, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Routine to calculate Jacobi polynomials, 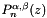 , and their first derivative,
, and their first derivative, 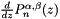 .
.
containing the value of the 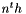 order Jacobi polynomial
order Jacobi polynomial
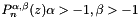 and its
and its
derivative at the np points in z[i]
relationship (see appendix A ref [4]) :
![$ \begin{array}{rcl} P^{\alpha,\beta}_0(z) &=& 1 \\ P^{\alpha,\beta}_1(z) &=& \frac{1}{2} [ \alpha-\beta+(\alpha+\beta+2)z] \\ a^1_n P^{\alpha,\beta}_{n+1}(z) &=& (a^2_n + a^3_n z) P^{\alpha,\beta}_n(z) - a^4_n P^{\alpha,\beta}_{n-1}(z) \\ a^1_n &=& 2(n+1)(n+\alpha + \beta + 1)(2n + \alpha + \beta) \\ a^2_n &=& (2n + \alpha + \beta + 1)(\alpha^2 - \beta^2) \\ a^3_n &=& (2n + \alpha + \beta)(2n + \alpha + \beta + 1) (2n + \alpha + \beta + 2) \\ a^4_n &=& 2(n+\alpha)(n+\beta)(2n + \alpha + \beta + 2) \end{array} $](form_127.png)
the relationship (see appendix A ref [4]) :
![$ \begin{array}{rcl} b^1_n(z)\frac{d}{dz} P^{\alpha,\beta}_n(z)&=&b^2_n(z)P^{\alpha,\beta}_n(z) + b^3_n(z) P^{\alpha,\beta}_{n-1}(z) \hspace{2.2cm} \\ b^1_n(z) &=& (2n+\alpha + \beta)(1-z^2) \\ b^2_n(z) &=& n[\alpha - \beta - (2n+\alpha + \beta)z]\\ b^3_n(z) &=& 2(n+\alpha)(n+\beta) \end{array} $](form_128.png)
Definition at line 1951 of file Polylib.cpp.
Referenced by Nektar::LibUtilities::Basis::GenBasis(), hgj(), hglj(), hgrjm(), hgrjp(), jacobd(), Jacobz(), main(), Nektar::MultiRegions::ExpList1D::PeriodicEval(), Nektar::LibUtilities::NodalUtilTriangle::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilTetrahedron::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilPrism::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilQuad::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilHex::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilTriangle::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilTetrahedron::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilPrism::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilQuad::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilHex::v_OrthoBasisDeriv(), zwglj(), zwgrjm(), and zwgrjp().
|
static |
Calculate the n zeros, z, of the Jacobi polynomial, i.e.
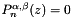
This routine is only value for 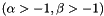
and uses polynomial deflation in a Newton iteration
Definition at line 2279 of file Polylib.cpp.
References EPS, jacobfd(), and STOP.
| void Polylib::JacZeros | ( | const int | n, |
| double * | a, | ||
| double * | b, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Zero and Weight determination through the eigenvalues and eigenvectors of a tridiagonal.
matrix from the three term recurrence relationship.
Set up a symmetric tridiagonal matrix
![$ \left [ \begin{array}{ccccc} a[0] & b[0] & & & \\ b[0] & a[1] & b[1] & & \\ 0 & \ddots & \ddots & \ddots & \\ & & \ddots & \ddots & b[n-2] \\ & & & b[n-2] & a[n-1] \end{array} \right ] $](form_137.png)
Where the coefficients a[n], b[n] come from the recurrence relation
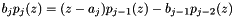
where 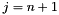 and
and 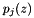 are the Jacobi (normalized)
are the Jacobi (normalized)
orthogonal polynomials 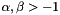 ( integer values and
( integer values and
halves). Since the polynomials are orthonormalized, the tridiagonal
matrix is guaranteed to be symmetric. The eigenvalues of this
matrix are the zeros of the Jacobi polynomial.
Definition at line 2389 of file Polylib.cpp.
References RecCoeff(), and TriQL().
| void Polylib::JKMatrix | ( | int | n, |
| double * | a, | ||
| double * | b | ||
| ) |
Calcualtes the Jacobi-kronrod matrix by determining the.
a and coefficients.
The first 3n+1 coefficients are already known
For more information refer to:
"Dirk P. Laurie, Calcualtion of Gauss-Kronrod quadrature rules"
Definition at line 2769 of file Polylib.cpp.
Referenced by zwgk(), zwlk(), and zwrk().
|
static |
The routine finds the recurrence coefficients a and.
b of the orthogonal polynomials
Definition at line 2449 of file Polylib.cpp.
References gammaF().
Referenced by JacZeros(), zwgk(), zwlk(), and zwrk().
|
static |
QL algorithm for symmetric tridiagonal matrix.
This subroutine is a translation of an algol procedure,
num. math. 12, 377-383(1968) by martin and wilkinson, as modified
in num. math. 15, 450(1970) by dubrulle. Handbook for
auto. comp., vol.ii-linear algebra, 241-248(1971). This is a
modified version from numerical recipes.
This subroutine finds the eigenvalues and first components of the
eigenvectors of a symmetric tridiagonal matrix by the implicit QL
method.
on input:
in its first n-2 positions.
on output:
e contains the weight values - modifications of the first component
of normalised eigenvectors
Definition at line 2565 of file Polylib.cpp.
References CellMLToNektar.cellml_metadata::p, sign, and STOP.
Referenced by JacZeros(), zwgk(), zwlk(), and zwrk().
| void Polylib::zwgj | ( | double * | z, |
| double * | w, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Gauss-Jacobi zeros and weights.
associated with the Jacobi polynomial 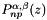 ,
,
Definition at line 107 of file Polylib.cpp.
References gammaF(), jacobd(), and jacobz.
Referenced by Nektar::LibUtilities::GaussPoints::CalculatePoints(), and main().
| void Polylib::zwgk | ( | double * | z, |
| double * | w, | ||
| const int | npt, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Gauss-Kronrod-Jacobi zeros and weights.
associated with the Jacobi polynomial 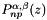 ,
,
Definition at line 385 of file Polylib.cpp.
References JKMatrix(), RecCoeff(), and TriQL().
Referenced by Nektar::LibUtilities::GaussPoints::CalculatePoints().
| void Polylib::zwglj | ( | double * | z, |
| double * | w, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Gauss-Lobatto-Jacobi zeros and weights with end point at z=-1,1.
associated with polynomial 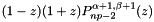
Definition at line 311 of file Polylib.cpp.
References gammaF(), jacobfd(), and jacobz.
Referenced by Nektar::LibUtilities::GaussPoints::CalculatePoints(), and main().
| void Polylib::zwgrjm | ( | double * | z, |
| double * | w, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Gauss-Radau-Jacobi zeros and weights with end point at z=-1.
associated with the polynomial 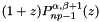 .
.
Definition at line 163 of file Polylib.cpp.
References gammaF(), jacobfd(), and jacobz.
Referenced by Nektar::LibUtilities::GaussPoints::CalculatePoints(), and main().
| void Polylib::zwgrjp | ( | double * | z, |
| double * | w, | ||
| const int | np, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Gauss-Radau-Jacobi zeros and weights with end point at z=1.
associated with the polynomial 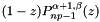 .
.
Definition at line 239 of file Polylib.cpp.
References gammaF(), jacobfd(), and jacobz.
Referenced by Nektar::LibUtilities::GaussPoints::CalculatePoints(), and main().
| void Polylib::zwlk | ( | double * | z, |
| double * | w, | ||
| const int | npt, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Gauss-Lobatto-Kronrod-Jacobi zeros and weights.
associated with the Jacobi polynomial 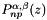 ,
,
Definition at line 711 of file Polylib.cpp.
References chri1(), JKMatrix(), RecCoeff(), and TriQL().
Referenced by Nektar::LibUtilities::GaussPoints::CalculatePoints().
| void Polylib::zwrk | ( | double * | z, |
| double * | w, | ||
| const int | npt, | ||
| const double | alpha, | ||
| const double | beta | ||
| ) |
Gauss-Radau-Kronrod-Jacobi zeros and weights.
associated with the Jacobi polynomial 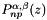 ,
,
Definition at line 519 of file Polylib.cpp.
References chri1(), JKMatrix(), RecCoeff(), and TriQL().
Referenced by Nektar::LibUtilities::GaussPoints::CalculatePoints().
 1.8.8
1.8.8