[prev] [prev-tail] [tail] [up]

Chapter 3
Stability analysis

3.1 Direct

In the folder $NEKTUTORIAL/stability/Direct there are the files that are required for the direct stability analysis. Since, the computation would normally take several hours to converge, we will use a restart file and a Krylov-space of just κ = 4. Therefore, it will be possible to obtain the eigenvalue and the corresponding eigenmode after 2 iterations.

Task: 3.1 Define a Kyrlov space of 4 and compute the leading 2 eigenvalues and the eigenvectors of the problem using Arpack and the restart file Cylinder_Direct.rst.

The simulation should converge in 6 iterations and the terminal screen should look similar to the one below:

======================================================================= 
                EquationType: UnsteadyNavierStokes 
                Session Name: Cylinder_Direct 
                Spatial Dim.: 2 
          Max SEM Exp. Order: 7 
              Expansion Dim.: 2 
             Projection Type: Continuous Galerkin 
                   Advection: explicit 
                   Diffusion: explicit 
                   Time Step: 0.0008 
                No. of Steps: 1250 
         Checkpoints (steps): 1000 
            Integration Type: IMEXOrder2 
======================================================================= 
        Arnoldi solver type    : Arpack 
        Arpack problem type    : LM 
        Single Fourier mode    : false 
        Beta set to Zero       : false 
        Evolution operator     : Direct 
        Krylov-space dimension : 4 
        Number of vectors      : 2 
        Max iterations         : 500 
        Eigenvalue tolerance   : 1e-06 
====================================================== 
Initial Conditions: 
  - Field u: from file Cylinder_Direct.rst 
  - Field v: from file Cylinder_Direct.rst 
  - Field p: from file Cylinder_Direct.rst 
Writing: "Cylinder_Direct_0.chk" 
        Inital vector       : input file 
Iteration 0, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk" 
Steps: 1250     Time: 1            CPU Time: 46.5477s 
Time-integration  : 46.5477s 
Writing: "Cylinder_Direct.fld" 
Iteration 1, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk" 
Steps: 1250     Time: 2            CPU Time: 41.7221s 
Time-integration  : 41.7221s 
Iteration 2, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk" 
Steps: 1250     Time: 3            CPU Time: 41.8717s 
Time-integration  : 41.8717s 
Iteration 3, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk" 
Steps: 1250     Time: 4            CPU Time: 41.9465s 
Time-integration  : 41.9465s 
Iteration 4, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk" 
Steps: 1250     Time: 5            CPU Time: 41.987s 
Time-integration  : 41.987s 
Iteration 5, output: 0, ido=1 
Writing: "Cylinder_Direct_1.chk" 
Steps: 1250     Time: 6            CPU Time: 42.2642s 
Time-integration  : 42.2642s 
Iteration 6, output: 0, ido=99 
Converged in 6 iterations 
Converged Eigenvalues: 2 
         Magnitude   Angle       Growth      Frequency 
EV: 0 0.9792      0.726586    -0.0210196  0.726586 
Writing: "Cylinder_Direct_eig_0.fld" 
EV: 1 0.9792      -0.726586   -0.0210196  -0.726586 
Writing: "Cylinder_Direct_eig_1.fld" 
L 2 error (variable u) : 0.0501837 
L inf error (variable u) : 0.0296123 
L 2 error (variable v) : 0.0635524 
L inf error (variable v) : 0.0355673 
L 2 error (variable p) : 0.0344665 
L inf error (variable p) : 0.0176009

Task: 3.2 Verify that the leading eigenvalues show a growth rate of σ = −2.10196 × 10−2 and a frequency ω = ±7.26586 × 10−1.
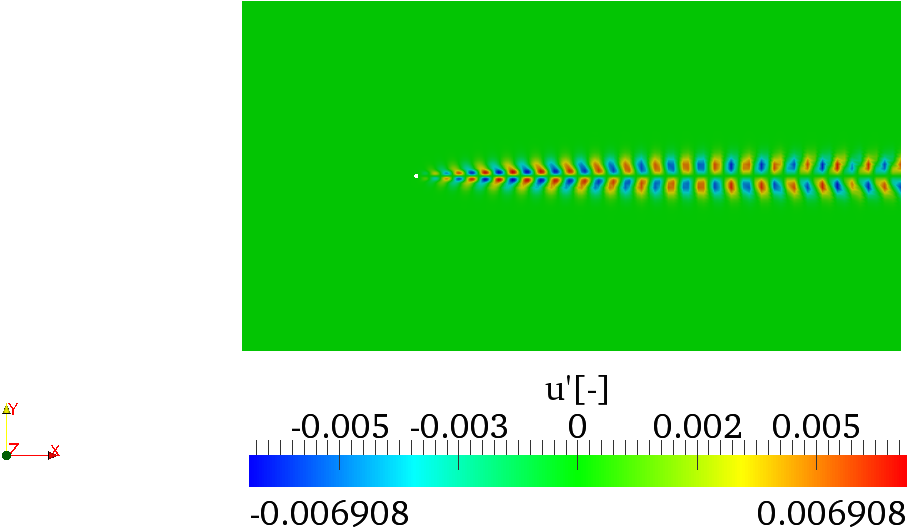
Task: 3.3 Plot the leading eigenvector in Paraview or VisIt. This should look like the solution shown in figures 3.1.

PIC PIC

Figure 3.1: u′-component and v′-component of the eigenmode

3.2 Adjoint

After the direct stability analysis, it is now interesting to compute the eigenvalues and eigenvectors of the adjoint operator A∗ that allows us to evaluate the effects of generic initial conditions and forcing terms on the asymptotic behaviour of the solution of the linearised equations. In the folder Cylinder/Stability/Adjoint there is the file Cylinder_Adjoint.xml that is used for the adjoint analysis.

Task: 3.4 Set the EvolutionOperator to Adjoint, the Krylov space to 4 and compute the leading eigenvalue and eigenmode of the adjoint operator, using the restart file Cylinder_Adjoint.rst

The solution should converge after 4 iterations and the terminal screen should look like this:

======================================================================= 
                EquationType: UnsteadyNavierStokes 
                Session Name: Cylinder_Adjoint 
                Spatial Dim.: 2 
          Max SEM Exp. Order: 7 
              Expansion Dim.: 2 
             Projection Type: Continuous Galerkin 
                   Advection: explicit 
                   Diffusion: explicit 
                   Time Step: 0.001 
                No. of Steps: 1000 
         Checkpoints (steps): 1000 
            Integration Type: IMEXOrder3 
======================================================================= 
        Arnoldi solver type    : Arpack 
        Arpack problem type    : LM 
        Single Fourier mode    : false 
        Beta set to Zero       : false 
        Evolution operator     : Adjoint 
        Krylov-space dimension : 4 
        Number of vectors      : 2 
        Max iterations         : 500 
        Eigenvalue tolerance   : 0.001 
====================================================== 
Initial Conditions: 
Field p not found. 
  - Field u: from file Cylinder_Adjoint.rst 
  - Field v: from file Cylinder_Adjoint.rst 
  - Field p: from file Cylinder_Adjoint.rst 
Writing: "Cylinder_Adjoint_0.chk" 
        Inital vector       : input file 
Iteration 0, output: 0, ido=1 Steps: 1000     Time: 27     CPU Time: 42.0192s 
Writing: "Cylinder_Adjoint_1.chk" 
Time-integration  : 42.0192s 
 
Writing: "Cylinder_Adjoint.fld" 
Iteration 1, output: 0, ido=1 Steps: 1000     Time: 28     CPU Time: 37.1084s 
Writing: "Cylinder_Adjoint_1.chk" 
Time-integration  : 37.1084s 
Iteration 2, output: 0, ido=1 Steps: 1000     Time: 29     CPU Time: 37.4794s 
Writing: "Cylinder_Adjoint_1.chk" 
Time-integration  : 37.4794s 
Iteration 3, output: 0, ido=1 Steps: 1000     Time: 30     CPU Time: 37.3142s 
Writing: "Cylinder_Adjoint_1.chk" 
Time-integration  : 37.3142s 
Iteration 4, output: 0, ido=99 
Converged in 4 iterations 
Converged Eigenvalues: 2 
         Magnitude   Angle       Growth      Frequency 
EV: 0 0.980493    0.727526    -0.0197     0.727526 
Writing: "Cylinder_Adjoint_eig_0.fld" 
EV: 1 0.980493    -0.727526   -0.0197     -0.727526 
Writing: "Cylinder_Adjoint_eig_1.fld" 
L 2 error (variable u) : 0.434746 
L inf error (variable u) : 0.156905 
L 2 error (variable v) : 0.698425 
L inf error (variable v) : 0.120624 
L 2 error (variable p) : 0.216948 
L inf error (variable p) : 0.0676028

Task: 3.5 Verify that the eigenvalues of the system are λ1,2 = 0.980495 ×e±i0.727502 with a growth rate equal to σ = −1.969727 × 10−2 and a frequency ω = ±7.275024 × 10−1.

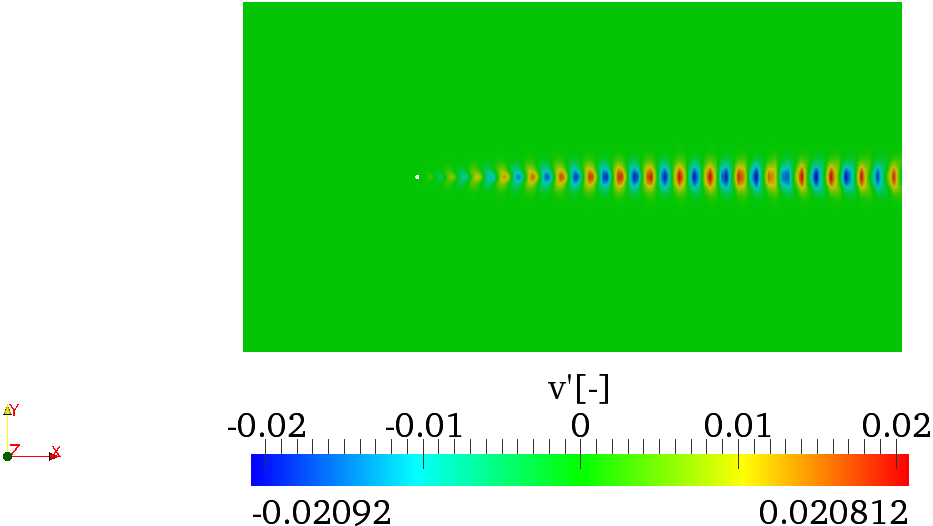
Task: 3.6 Plot the leading eigenmode in Paraview or VisIt that should look like figures 3.2 and 3.2.

Note that, in spatially developing flows, the eigenmodes of the direct stability operator tend to be located far downstream while the eigenmodes of the adjoint operator tend to be located upstream and near to the body, as can be seen in figures 3.2 and 3.3. From the profiles of the eigemodes, it can be deducted that the regions with the maximum receptivity for the momentum forcing and mass injection are near the wake of the cylinder, close to the upper and lower sides of the body surface, in accordance with results reported in the literature.

PIC

Figure 3.2: Close-up of the u∗-component of the adjoint eigenmode.

PIC

Figure 3.3: The v∗-component of the adjoint eigenmode extends far upstream of the cylinder

[prev] [prev-tail] [front] [up]