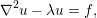
Welcome to the tutorial on solving the Helmholtz problem using the Advection-Diffusion-Reaction (ADR) Solver in the Nektar++ framework. This tutorial is aimed to show the main features of the ADR solver in a simple manner. If you have not already downloaded and installed Nektar++, please do so by visiting http://www.nektar.info, where you can also find the User-Guide with the instructions to install the library.
This tutorial requires:
After the completion of this tutorial, you will be familiar with:
/usr/bin. If
you compile from source they will be in the sub-directory dist/bin of the build
directory you created in the Nektar++ source tree. We will refer to the directory
containing the executables as $NEK for the remainder of the tutorial.
tar -xzvf basics-helmholtz.tar.gz to produce a directory
basics-helmholtz with subdirectories called tutorial and complete.
We will refer to the tutorial directory as $NEKTUTORIAL.
The tutorial folder contains:
Helm_mesh.geo;
Helm_mesh.msh;
The ADR solver can solve various problems, including the unsteady advection, unsteady diffusion, unsteady advection diffusion equation, etc. For a more detailed description of this solver, please refer to the User-Guide.
In this tutorial we focus on the Helmholtz equation
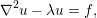 | (1.1) |
where u is the independent variable. The Helmholtz equation can be solved in one, two and three spatial dimensions. We will here consider a two-dimensional problem.
The problem we want to solve consists of known boundary conditions and forcing function which depend on x and y. To model this problem we create a computational domain also referred to as mesh or grid (see section 2) on which we apply the following two-dimensional function with Dirichlet and Neumann boundary conditions.
![2 2
∇ u − λu = − (2π + λ)cos(πx )cos(πy ),
u (x,y ) = cos(πx)cos(πy),
u (xb = ±1, yb) = cos(πxb)cos(πyb),
∂-u(xb,yb = ±1) = ± ∂-u(xb,yb = ±1) = ∓ π[cos(πxb )sin(πyb)]
dn dy](basics-helmholtz1x.png) | (1.2) |
where xb and yb represent the boundaries of the computational domain (see section 2.1) and λ is a positive constant.
We will set the boundary conditions and forcing function for this solver (see section 2.1) then, after running the solver (see section 3) we will post-process the data in order to visualise the results (see section 4).