Chapter 3
Stability analysis
3.1 Direct
In the folder $NEKTUTORIAL/stability/Direct there are the files that are required for the
direct stability analysis. Since, the computation would normally take several hours to
converge, we will use a restart file and a Krylov-space of just κ = 4. Therefore, it
will be possible to obtain the eigenvalue and the corresponding eigenmode after 2
iterations.
Task: 3.1 Define a Kyrlov space of 4 and compute the leading 2 eigenvalues and the
eigenvectors of the problem using Arpack and the restart file Cylinder_Direct.rst.
The simulation should converge in 6 iterations and the terminal screen should look similar to
the one below:
=======================================================================
EquationType: UnsteadyNavierStokes
Session Name: Cylinder_Direct
Spatial Dim.: 2
Max SEM Exp. Order: 7
Expansion Dim.: 2
Projection Type: Continuous Galerkin
Advection: explicit
Diffusion: explicit
Time Step: 0.0008
No. of Steps: 1250
Checkpoints (steps): 1000
Integration Type: IMEXOrder2
=======================================================================
Arnoldi solver type : Arpack
Arpack problem type : LM
Single Fourier mode : false
Beta set to Zero : false
Evolution operator : Direct
Krylov-space dimension : 4
Number of vectors : 2
Max iterations : 500
Eigenvalue tolerance : 1e-06
======================================================
Initial Conditions:
- Field u: from file Cylinder_Direct.rst
- Field v: from file Cylinder_Direct.rst
- Field p: from file Cylinder_Direct.rst
Writing: "Cylinder_Direct_0.chk"
Inital vector : input file
Iteration 0, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk"
Steps: 1250 Time: 1 CPU Time: 46.5477s
Time-integration : 46.5477s
Writing: "Cylinder_Direct.fld"
Iteration 1, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk"
Steps: 1250 Time: 2 CPU Time: 41.7221s
Time-integration : 41.7221s
Iteration 2, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk"
Steps: 1250 Time: 3 CPU Time: 41.8717s
Time-integration : 41.8717s
Iteration 3, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk"
Steps: 1250 Time: 4 CPU Time: 41.9465s
Time-integration : 41.9465s
Iteration 4, output: 0, ido=1 Writing: "Cylinder_Direct_1.chk"
Steps: 1250 Time: 5 CPU Time: 41.987s
Time-integration : 41.987s
Iteration 5, output: 0, ido=1
Writing: "Cylinder_Direct_1.chk"
Steps: 1250 Time: 6 CPU Time: 42.2642s
Time-integration : 42.2642s
Iteration 6, output: 0, ido=99
Converged in 6 iterations
Converged Eigenvalues: 2
Magnitude Angle Growth Frequency
EV: 0 0.9792 0.726586 -0.0210196 0.726586
Writing: "Cylinder_Direct_eig_0.fld"
EV: 1 0.9792 -0.726586 -0.0210196 -0.726586
Writing: "Cylinder_Direct_eig_1.fld"
L 2 error (variable u) : 0.0501837
L inf error (variable u) : 0.0296123
L 2 error (variable v) : 0.0635524
L inf error (variable v) : 0.0355673
L 2 error (variable p) : 0.0344665
L inf error (variable p) : 0.0176009
Task: 3.2 Verify that the leading eigenvalues show a growth rate of σ = −2.10196 × 10−2
and a frequency ω = ±7.26586 × 10−1.
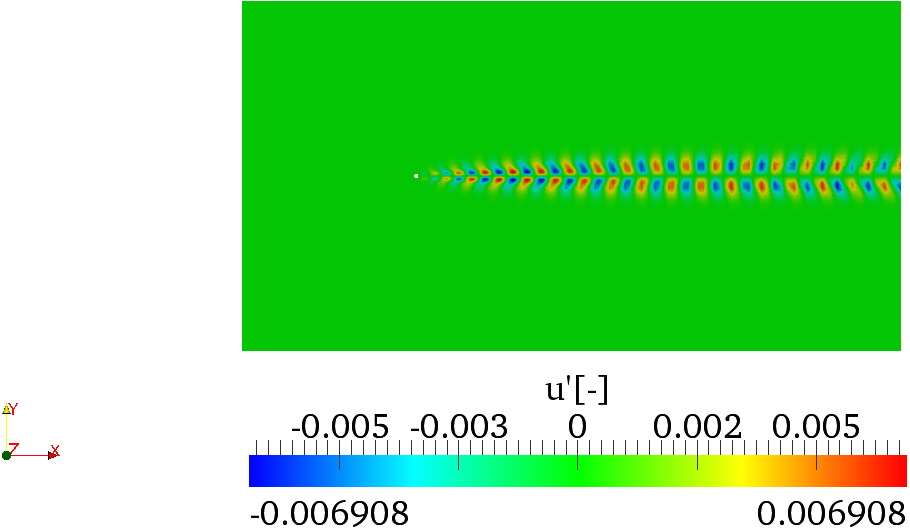
Task: 3.3 Plot the leading eigenvector in
Paraview or VisIt. This should look like the
solution shown in figures
3.1.
3.2 Adjoint
After the direct stability analysis, it is now interesting to compute the eigenvalues and
eigenvectors of the adjoint operator A∗ that allows us to evaluate the effects of generic initial
conditions and forcing terms on the asymptotic behaviour of the solution of the
linearised equations. In the folder Cylinder/Stability/Adjoint there is the file
Cylinder_Adjoint.xml that is used for the adjoint analysis.
Task: 3.4 Set the EvolutionOperator to Adjoint, the Krylov space to 4 and compute
the leading eigenvalue and eigenmode of the adjoint operator, using the restart file
Cylinder_Adjoint.rst
The solution should converge after 4 iterations and the terminal screen should look like this:
=======================================================================
EquationType: UnsteadyNavierStokes
Session Name: Cylinder_Adjoint
Spatial Dim.: 2
Max SEM Exp. Order: 7
Expansion Dim.: 2
Projection Type: Continuous Galerkin
Advection: explicit
Diffusion: explicit
Time Step: 0.001
No. of Steps: 1000
Checkpoints (steps): 1000
Integration Type: IMEXOrder3
=======================================================================
Arnoldi solver type : Arpack
Arpack problem type : LM
Single Fourier mode : false
Beta set to Zero : false
Evolution operator : Adjoint
Krylov-space dimension : 4
Number of vectors : 2
Max iterations : 500
Eigenvalue tolerance : 0.001
======================================================
Initial Conditions:
Field p not found.
- Field u: from file Cylinder_Adjoint.rst
- Field v: from file Cylinder_Adjoint.rst
- Field p: from file Cylinder_Adjoint.rst
Writing: "Cylinder_Adjoint_0.chk"
Inital vector : input file
Iteration 0, output: 0, ido=1 Steps: 1000 Time: 27 CPU Time: 42.0192s
Writing: "Cylinder_Adjoint_1.chk"
Time-integration : 42.0192s
Writing: "Cylinder_Adjoint.fld"
Iteration 1, output: 0, ido=1 Steps: 1000 Time: 28 CPU Time: 37.1084s
Writing: "Cylinder_Adjoint_1.chk"
Time-integration : 37.1084s
Iteration 2, output: 0, ido=1 Steps: 1000 Time: 29 CPU Time: 37.4794s
Writing: "Cylinder_Adjoint_1.chk"
Time-integration : 37.4794s
Iteration 3, output: 0, ido=1 Steps: 1000 Time: 30 CPU Time: 37.3142s
Writing: "Cylinder_Adjoint_1.chk"
Time-integration : 37.3142s
Iteration 4, output: 0, ido=99
Converged in 4 iterations
Converged Eigenvalues: 2
Magnitude Angle Growth Frequency
EV: 0 0.980493 0.727526 -0.0197 0.727526
Writing: "Cylinder_Adjoint_eig_0.fld"
EV: 1 0.980493 -0.727526 -0.0197 -0.727526
Writing: "Cylinder_Adjoint_eig_1.fld"
L 2 error (variable u) : 0.434746
L inf error (variable u) : 0.156905
L 2 error (variable v) : 0.698425
L inf error (variable v) : 0.120624
L 2 error (variable p) : 0.216948
L inf error (variable p) : 0.0676028
Task: 3.5 Verify that the eigenvalues of the system are λ1,2 = 0.980495 ×e±i0.727502 with a
growth rate equal to σ = −1.969727 × 10−2 and a frequency ω = ±7.275024 × 10−1.
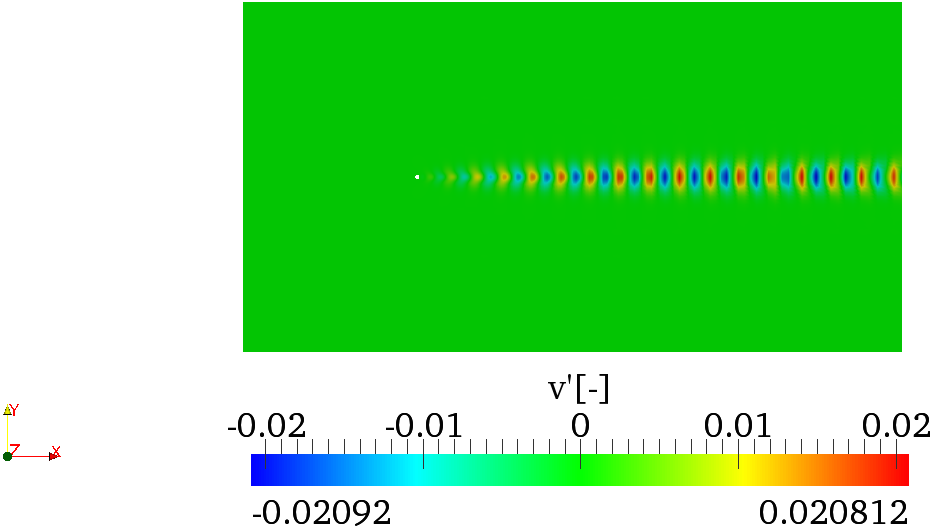
Task: 3.6 Plot the leading eigenmode in
Paraview or VisIt that should look like figures
3.2
and
3.2.
Note that, in spatially developing flows, the eigenmodes of the direct stability operator tend to
be located far downstream while the eigenmodes of the adjoint operator tend to be located
upstream and near to the body, as can be seen in figures 3.2 and 3.3. From the profiles of the
eigemodes, it can be deducted that the regions with the maximum receptivity for the
momentum forcing and mass injection are near the wake of the cylinder, close to the upper
and lower sides of the body surface, in accordance with results reported in the literature.