Chapter 2
Differentiation

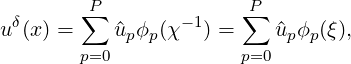
Assuming a polynomial approximation of the form:

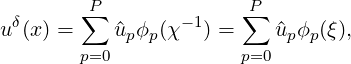
where χ(ξ) is the mapping from the standard region ξ ∈ Ω^s to the region containing x in the interval [a,b], we can differentiate u(x) using the chain rule to obtain

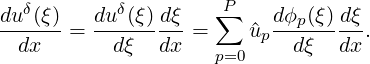
The differentiation of u^δ(x) is therefore dependent on evaluating dϕ_p(ξ)∕dξ and 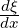. In this section we shall consider the case where ϕ_p(ξ) is the Lagrange polynomial h_p(ξ) and discuss how to evaluate dϕ_p(ξ)∕dξ. If χ(ξ) is an isoparametric mapping this technique can also be used to evaluate = ^-1. Differentiation of this form is often referred to as differentiation in physical space or collocation differentiation.

If we assume that u^δ(ξ) is a polynomial of order equal to or less than P [that is, u^δ(ξ) ∈ P_P ([-1,1])], then it can be exactly expressed in terms of Lagrange polynomials h_i(ξ) through a set of q nodal points ξ_i (0 ≤ i ≤ q - 1) as

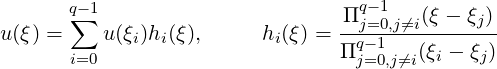
where q ≥ P + 1. Therefore the derivative of u(ξ) can be represented as

Typically, we only require the derivative at the nodal points ξ_i which is given by

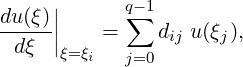
where

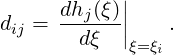
An alternative representation of the Lagrange polynomial is

Taking the derivative of h_i(ξ) we obtain

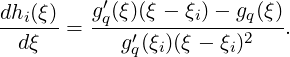
Finally, noting that because numerator and denominator of this expression are zero as ξ → ξ_i, and because P_q(ξ_i) = 0 by definition,

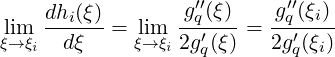
so we can write d_ij as

(2.1)

Equation (2.1) is the general representation of the derivative of the Lagrange polynomials evaluated at the nodal points ξ_i (0 ≤ i ≤ q - 1). To proceed further we need to know specific information about the nodal points ξ_i which will allow us to deduce alternative forms of g′_q(ξ_i) and g′′_q(ξ_i).

2.1 Legendre Formulae

The most common differentiation matrices d_ij are those corresponding to the Gauss-Legendre quadrature points. In this section we illustrate the final form of the differential matrices that correspond to the use of Gauss-Legendre, Gauss-Radau-Legendre, and Gauss-Lobatto-Legendre quadrature points. Denoting by ξ_i,P ^α,β the P zeros of the Jacobi polynomial P_P ^α,β(ξ) such that

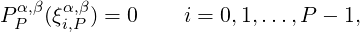
the derivative matrix d_ij used to evaluate 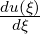at ξ_i, that is,

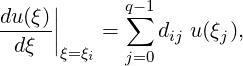
is defined as:

(1) Gauss-Legendre

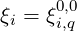
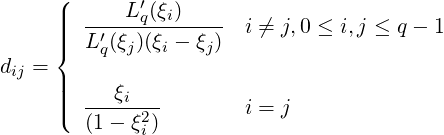
(2) Gauss-Radau-Legendre

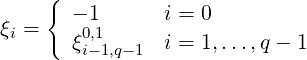
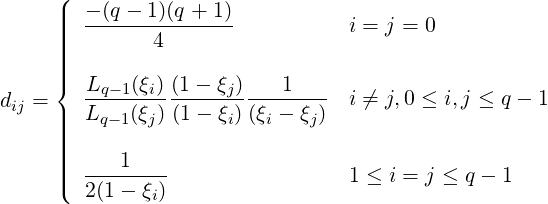
(3) Gauss-Lobatto-Legendre

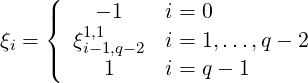
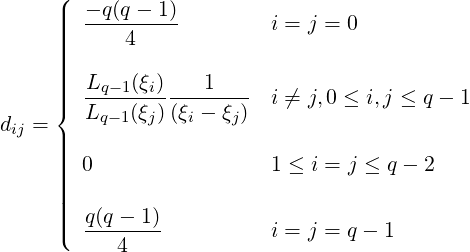
In a similar way to the quadrature formulae the construction of the differen- tiation matrices require the quadrature zeros to be determined numerically. Having determined the zeros, the components of the differentiation matrix can be evaluated directly from the above formulae by generating the Legendre polynomial from the recursion relationship.