[prev] [prev-tail] [tail] [up]

Chapter 3
Computational Exercises

3.1 One dimensional differentiation in a standard segment

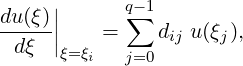
In this first exercise we will demonstrate how to differentiate the function f(ξ) = ξ7 in the standard segment ξ ∈ [-1,1] using Gaussian quadrature. The Gaussian quadrature zeros and the differentiation matrix are coded in the LIbUtilities library and for future reference this can be found under the directory $NEKDIST/library/LibUtilities/Foundations/. For the following exercises we will access the zeros and differentiation matrix from the PointsManager. The PointsManager is a type of map (or manager) which requires a key defining known Gaussian quadrature types called PointsKey.

In the $NEKDIST/tutorial/fundamentals-differentiation/tutorial directory open the file named StdDifferentiation1D.cpp. Look over the comments supplied in the file which outline how to define the number of quadrature points to apply, the type of Gaussian quadrature, a differentiation matrix and some arrays to hold the zeros and solution. Finally a PointsKey is defined which is then used to obtain the zeros in an array called quadZeros and the differentiation matrix in a pointer to a matrix called derivMatrix.

Task: 3.1

Implement a short block of code where you see the comments “Write your code here” which evaluates the loop

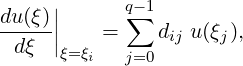
du(ξ)|| q∑-1 --dξ-|| = dij u (ξj), ξ=ξi j=0

Tip: To access individual elements in MatrixSharedPtrType, the pointer must first be dereferenced then accessed using the parantheses operator. This should look like (*derivMatrix)(i, j). On the other hand, to access elements in Array<OneD, NekDouble>, the bracket operator can be directly used such as quadZerosDir1[i]. If the array is two-dimensional (Array<TwoD, NekDouble>), elements would be accessed through quadDerivsDir1[i][j].

To compile your code type

make StdDifferentiation1D

in the tutorial directory. When your code compiles successfully1 then type

./StdDifferentiation1D

You should now get some output similar to

====================================================== 
|      DIFFERENTIATION IN A 1D STANDARD REGION       | 
====================================================== 
Differentiate the function f(xi) = xi^7 in the 
standard segment xi=[-1,1] using quadrature points 
         Q = 7: Error = 1.49647

Task: 3.2 Evaluate the previous derivatives for a quadrature order of Q = Qmax where Qmax = 8 is the number of quadrature points required for an exact evaluation of the derivatives (calculate this value analytically). Verify that the error is zero (up to numerical precision).

We can also use Gauss-Lobatto-Legendre type differentiation rather than Gauss-Legendre type in the previous exercises. To do this we replace

LibUtilities::PointsType quadPointsType = 
                        LibUtilities::eGaussGaussLegendre;

with

LibUtilities::PointsType quadPointsType = 
                        LibUtilities::eGaussLobattoLegendre;

3.2 Two-dimensional differentiation in a standard and local region

3.2.1 Quadrilateral element in a standard region

A straightforward extension of the one-dimensional Gaussian rule is to the two-dimensional standard quadrilateral region and similarly to the three-dimensional hexahedral region. Differentiation in Q2 = {-1 ≤ ξ1,ξ2 ≤ 1} in the ξ1 direction is defined as

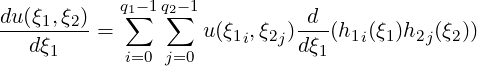
q -1q -1 du(ξ1,ξ2) 1∑ 2∑ -d- dξ1 = u(ξ1i,ξ2j)dξ1(h1i(ξ1)h2j(ξ2)) i=0 j=0

where h1 and h2 are the polynomials associated respectively with coordinates ξ1 and ξ2.

Because h2 is not a function of ξ1, we can rewrite the formula as

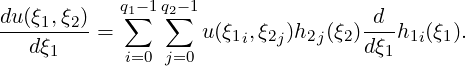q1- 1q2- 1 du-(ξ1,ξ2) = ∑ ∑ u(ξ ,ξ )h (ξ )-d-h (ξ ). dξ1 i=0 j=0 1i 2j 2j 2 dξ1 1i 1
(3.1)

Typically, we only require the derivative at the nodal points (ξ1i,ξ2j). At these points, h2 has trivial values, i.e. unit value at ξ2j and null value at all other points. The summation over j therefore drops and we are left with the same formula as in our one-dimensional problem

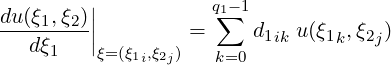du(ξ1,ξ2)|| q1∑-1 ---------|| = d1ik u (ξ1k,ξ2j) dξ1 ξ=(ξ1i,ξ2j) k=0
(3.2)

where d1ik is the differentiation matrix in the ξ1 direction such that

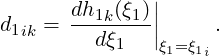
| d = dh1k(ξ1)|| . 1ik dξ1 |ξ1=ξ1i

Likewise, the derivative with respect to ξ2 can be expressed by

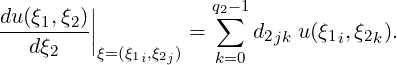
| q2-1 du(ξ1,ξ2)-|| = ∑ d u (ξ ,ξ ). dξ2 |ξ=(ξ1i,ξ2j) 2jk 1i 2k k=0

Task: 3.3 Differentiate the function f(ξ1,ξ2) = ξ17 ξ29 in the standard quadrilateral element Q ∈ [-1,1] × [-1,1] using Gaussian quadrature points.

Using a series of one-dimensional Gaussian quadrature rules as outlined above evaluate the derivative in each direction and for each quadrature point by completing the first part of the code in the file StdDifferentiation2D.cpp in the directory

$NekDist/tutorial/fundamentals-differentiation/tutorial.

The quadrature zeros and differentiation matrices in each of the coordinate directions have already been setup and are initially set to q1 = 7,q2 = 9 using a Gauss-Lobatto-Legendre quadrature rule. Complete the code by writing a structure of loops which implement the two-dimensional Gaussian quadrature rule2 . The expected output is given below). Also verify that the error is zero when q1 = 8,q2 = 10.

Recall that to compile the file you type

make StdDifferentiation2D

When executing the tutorial with the quadrature order q1 = 7,q2 = 9 you should get an output of the form:

=========================================================== 
|    DIFFERENTIATION IN 2D ELEMENT in Standard Region     | 
=========================================================== 
 
Differentiate the function f(x1,x2) = (x1)^7*(x2)^9 
on the standard quadrilateral element: 
         q1 = 7, q2 = 9: Error = 7.19196

3.2.2 General straight-sided quadrilateral element

PIC

Figure 3.1: To construct a C0 expansion from multiple elements of specified shapes (for example, triangles or rectangles), each elemental region Ωe is mapped to a standard region Ωst in which all local operations are evaluated.

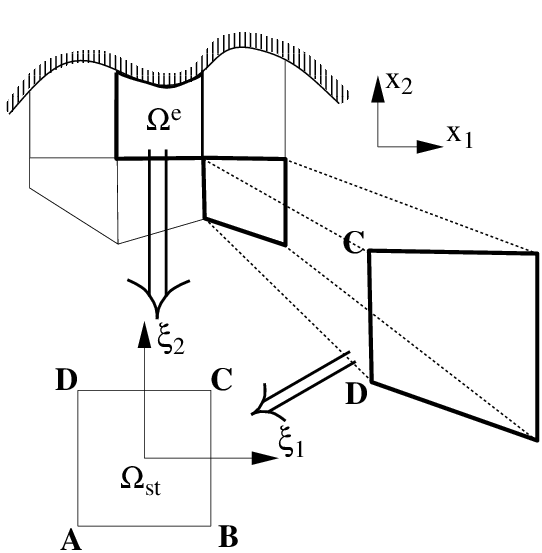
For elemental shapes with straight sides a simple mapping may be constructed using a linear mapping similar to the vertex modes of a hierarchical/modal expansion. For the straight-sided quadrilateral with vertices labeled as shown in figure 3.1(b) the mapping can be defined as:

(1 - ξ )(1- ξ ) (1 + ξ )(1- ξ ) xi = χi(ξ1,ξ2) = xAi------1------2--+ xBi------1------2-- 2 2 2 2 +xD (1---ξ1)-(1+-ξ2)+ xC(1-+-ξ1)(1+-ξ2). i = 1,2 (3.3) i 2 2 i 2 2

We denote an arbitrary quadrilateral region by Ωe which is a function of the global Cartesian coordinate system (x1,x2) in two-dimensions. To differentiate in Ωe we transform this region into the standard region Ωst defined in terms of (ξ1,ξ2). We begin with the basic definition of differentiation:

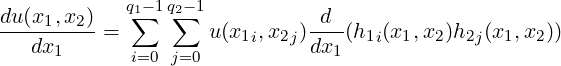
q- 1q- 1 du(x1,x2)- ∑1 ∑2 -d-- dx1 = u(x1i,x2j)dx1 (h1i(x1,x2)h2j(x1,x2)) i=0 j=0

Unlike differentiation in the standard region, both h1 and h2 are functions of both local coordinates. The chain rule can be applied to obtain a system similar to the previous exercise:

du(x1,x2) q∑1- 1q∑2- 1 dξ1 d dξ2 d ---dx-----= u(x1i,x2j)[h2j(ξ2)dx--dξ-h1i(ξ1)) + h1i(ξ1)dx--dξ-h2j(ξ2))] 1 i=0 j=0 1 1 1 2
(3.4)

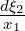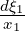where h1 and h2 are functions of ξ1 and ξ2 respectively only and where dξ2- x1 and dξ1 x1 come from the inverse two-dimensional Jacobian matrix due to the transformation, defined as:

⌊ ⌋ ⌊ ⌋ ∂x1- ∂x1- -1 ∂ξ1- ∂-ξ1- -1 || ∂ξ1 ∂ξ2 || || ∂x1 ∂x2 || J2D = ⌈ ∂x2- ∂x2- ⌉ = ⌈ ∂ξ2- ∂-ξ2- ⌉ ∂ξ1 ∂ξ2 ∂x1 ∂x2

As we have assumed that we know the form of the mapping [i.e., x1 = χ1(ξ1,ξ2), x2 = χ2(ξ1,ξ2)] we can evaluate all the partial derivatives required to determine the Jacobian matrix. If the elemental region is straight-sided then we have seen that a mapping from (x1,x2) → (ξ1,ξ2) is given by equations (3.3).

Equation (3.4) turns out to be similar to equation (3.1) in the standard region and can be also rewritten in the style of equation (3.2):

| | q-1 du(x1,x2)|| -dξ1|| 1∑ dx1 |x= (x1 ,x2) = dx1 |x= (x1 ,x2) d1ik u(x1k,x2j) i j | i j k=0 -dξ2|| q2∑-1 + dx1 |x= (x ,x ) d2jk u(x1i,x2k ) (3.5) 1i 2j k=0

Similarly to the differentiation in the standard region, derivatives with respect to the other local coordinate can also be found by substituting dx2 for dx1. We can also note that equation (3.2) is a particular case of equation (3.5) where 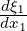ddξx1 1 = 1 and 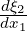ddxξ2- 1 = 0. This effectively corresponds to the situation where the local region has the same shape and dimensions as the standard region (with the admission of a translation in the plane).

Task: 3.4 We now consider how to differentiate the function f(x1,x2) = x17 x29 in a local rectangular quadrilateral element. Consider the local quadrilateral element with vertices

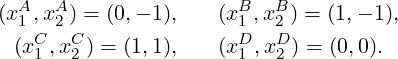
(xA1 ,xA2) = (0,- 1), (xB1 ,xB2 ) = (1,- 1), (xC,xC ) = (1,1), (xD ,xD) = (0,0). 1 2 1 2

This is clearly similar to the previous exercise. However, as we are calculating the derivatives of a function defined in a local element rather than in a reference element, we have to take into account the geometry of the element. Therefore, the implementation is altered in two ways:

  1. The quadrature zeros should be transformed to local coordinates to evaluate the function f(x1,x2) at the quadrature points.
  2. Elements of the inverse Jacobian matrix of the transformation between local and reference coordinates should be taken into account when evaluating the derivatives.

In the file LocDifferentiation2D.cpp you are provided with the same set up as the previous task but now with a definition of the coordinate mapping included. Evaluate the expression for the Jacobian matrix analytically and find its inverse. Then write a line of code in the loop for the Jacobian as indicated by the comments “Write your code here”. When you have written your expression you can compile the code with the command

make LocDifferentiation2D

Using the quadrature order specified in the file your output should look like:

========================================================= 
|     DIFFERENTIATION IN 2D ELEMENT in Local Region     | 
========================================================= 
 
Differentiate the function f(x1,x2) = x1^7 * x2^9 
in a local quadrilateral element: 
         q1 = 8, q2 = 10: Average Error = 0.0346594

Advanced Task: 3.5

As it turns out in the previous task, the average error is not equal to zero. Why is that?

Try different values of q1 and q2 and plot the average error with respect to these two parameters, either one by one or simultaneously. Why are the values of q1max and q2max (at which the average error reaches computer precision) different from those expected in the standard region?3

[prev] [prev-tail] [front] [up]