[prev] [prev-tail] [tail] [up]

Chapter 3
Stability analysis

We will now perform transient growth analysis with a Krylov subspace of kdim=4. The parameters and properties needed for this are present in the file bfs_tg.xml in $NEKTUTORIAL/stability. In this case the Arpack library was used to compute the largest eigenvalue of the system and the corresponding eigenmode. We will compute the maximum growth for a time horizon of τ = 1, usually denoted G(1).

Task: 3.1 Configure the bfs_tg.xml session for performing transient growth analysis:

Now run the simulation

IncNavierStokesSolver bfs_tg.xml

The terminal screen should look like this: 

======================================================================= 
                EquationType: UnsteadyNavierStokes 
                Session Name: bfs_tg 
                Spatial Dim.: 2 
          Max SEM Exp. Order: 7 
              Expansion Dim.: 2 
             Projection Type: Continuous Galerkin 
                   Advection: explicit 
                   Diffusion: explicit 
                   Time Step: 0.002 
                No. of Steps: 500 
         Checkpoints (steps): 500 
            Integration Type: IMEXOrder2 
======================================================================= 
        Arnoldi solver type    : Arpack 
        Arpack problem type    : LM 
        Single Fourier mode    : false 
        Beta set to Zero       : false 
        Evolution operator     : TransientGrowth 
        Krylov-space dimension : 4 
        Number of vectors      : 1 
        Max iterations         : 500 
        Eigenvalue tolerance   : 1e-06 
====================================================== 
Initial Conditions: 
Field p not found. 
Field p not found. 
  - Field u: from file bfs_tg.rst 
  - Field v: from file bfs_tg.rst 
  - Field p: from file bfs_tg.rst 
Writing: "bfs_tg_0.chk" 
        Inital vector       : input file 
Iteration 0, output: 0, ido=1 Steps: 500      Time: 1     CPU Time: 10.4384s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 10.4384s 
Steps: 500      Time: 29           CPU Time: 8.96463s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 8.96463s 
Writing: "bfs_tg.fld" 
Iteration 1, output: 0, ido=1 Steps: 500      Time: 2     CPU Time: 8.90168s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 8.90168s 
Steps: 500      Time: 30           CPU Time: 8.90607s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 8.90607s 
Iteration 2, output: 0, ido=1 Steps: 500      Time: 3     CPU Time: 8.96875s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 8.96875s 
Steps: 500      Time: 31           CPU Time: 8.92276s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 8.92276s 
Iteration 3, output: 0, ido=1 Steps: 500      Time: 4     CPU Time: 8.92597s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 8.92597s 
Steps: 500      Time: 32           CPU Time: 8.96103s 
Writing: "bfs_tg_1.chk" 
Time-integration  : 8.96103s 
Iteration 4, output: 0, ido=99 
Converged in 4 iterations 
Converged Eigenvalues: 1 
         Magnitude   Angle       Growth      Frequency 
EV: 0 3.23586     0           1.1743      0 
Writing: "bfs_tg_eig_0.fld" 
L 2 error (variable u) : 0.0118694 
L inf error (variable u) : 0.0118647 
L 2 error (variable v) : 0.0174185 
L inf error (variable v) : 0.0244285 
L 2 error (variable p) : 0.0109063 
L inf error (variable p) : 0.0138423

Initially, the solution will be evolved forward in time using the operator A , then backward in time through the adjoint operator A*.

Task: 3.2 Verify that the leading eigenvalue is equal to λ = 3.23586.
The leading eigenvalue corresponds to the largest possible transient growth at the time horizon τ = 1. The leading eigenmode is shown in figures 3.1 and 3.2. This is the optimal initial condition which will lead to the greatest growth when evolved under the linearised Navier-Stokes equations.

PIC

Figure 3.1: u′-component of the eigenmode

PIC

Figure 3.2: v′-component of the eigenmode

We can visualise graphically the optimal growth, recalling that the energy of the perturbation field at any given time t is defined by means of the inner product:

1 ′ ′ 1 ∫ ′ ′ E (τ) = 2(u (t),u (t)) = 2- u ⋅u dv Ω
(3.1)

The solver can output the evolution of the energy of the perturbation in time by using the ModalEnergy filter (defined in the FILTERS section of the XML file): 

1<FILTER TYPE="ModalEnergy"> 
2   <PARAM NAME="OutputFile">energy</PARAM> 
3   <PARAM NAME="OutputFrequency">10</PARAM> 
4</FILTER>

This will write the energy of the perturbation every 10 time steps to the file energy.mld. Repeating these simulations for different τ with the optimal initial perturbation as the initial condition, it is possible to create a plot similar to figure 3.3. Each curve necessarily meets the optimal growth envelope (denoted by the circles) at its corresponding value of τ, and never exceeds it.

The $NEKTUTORIAL/energy folder contains the files bfs_energy_tau01.xml and bfs_energy_tau20.xml, as well as the pre-computed optimal initial condition for τ = 20 (bfs_energy_tau20.rst), with corresponding optimal growth of 2172.9.

PIC

Figure 3.3: Envelope of two-dimensional optimal at Re = 500 together with curves of linear energy evolution starting from the three optimal initial conditions for specific values of τ 20, 60 and 100. Figure reproduced from J. Fluid. Mech. (2008), vol 603, pp. 271-304.

Task: 3.3 (Advanced/Optional) Generate energy curves for the optimal initial condition (leading eigenmode) computed in the previous task for τ = 1, and for τ = 20.

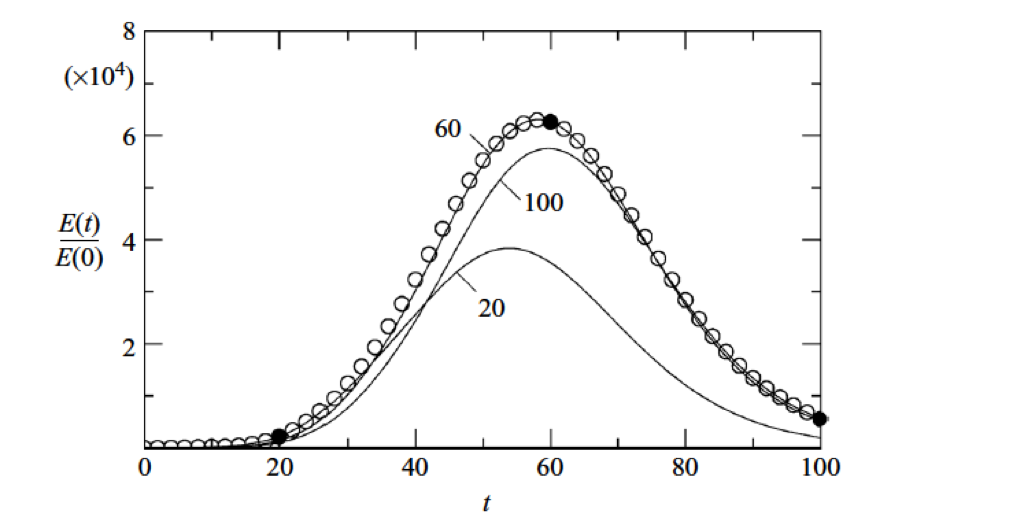
Use your favourite plotting program (e.g. MATLAB or GNUPlot) to read in the files produced by the energy filter and plot the normalised energy growth curves.

Tip: You will need to switch to using the Standard driver. You should also use the Direct evolution operator for this task, similar to the channel example.

Examine your plot. Verify the energy at time t = τ matches the optimal growth in each case. Now examine the plot at time t = 1. Note that although the overall energy growth for the τ = 20 curve is far greater than the corresponding τ = 1 curve, the τ = 1 curve has greater growth at t = τ = 1.

[prev] [prev-tail] [front] [up]