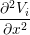 + giy
+ giy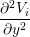
![[ ∂(V - V ) ]
Cm ---i----e-+ Gm (Vi - Ve)
∂t](user-guide37x.png)
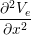 + gey
+ gey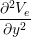
![[ ]
∂(Vi --Ve)
Cm ∂t + Gm (Vi - Ve)](user-guide40x.png) .
.The CardiacEPSolver is used to model the electrophysiology of cardiac tissue, specifically using the monodomain or bidomain model. These models are continuum models and represent an average of the electrical activity over many cells. The system is a reaction-diffusion system, with the reaction term modeling the flow of current in and out of the cells using a separate set of ODEs.
The Bidomain model is given by the following PDEs,
gix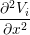 + giy + giy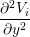 | = χ![[ ∂(V - V ) ]
Cm ---i----e-+ Gm (Vi - Ve)
∂t](user-guide37x.png) | ||
gex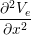 + gey + gey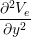 | = -χ![[ ]
∂(Vi --Ve)
Cm ∂t + Gm (Vi - Ve)](user-guide40x.png) . . |
χ![[ ∂Vm ]
Cm -∂t- + Jion](user-guide41x.png) | = gex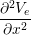 + gey + gey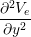 | ||
(gix + gex)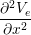 + (giy + gey) + (giy + gey)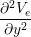 | = -gix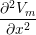 - giy - giy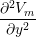 |
In the case where the intracellular and extracellular conductivities are proportional, that is gix = kgex for some k, then the above two PDEs can be reduced to a single PDE:
χ![[ ]
∂Vm-
Cm ∂t + Jion](user-guide48x.png) | = ∇⋅ (σ∇V m) |
The action potential of a cardiac cell can be modelled at either a biophysical level of detail, including a number of transmembrane currents, or as a phenomenological model, to reproduce the features of the action potential, with fewer variables. Each cell model will include a unique system of ODEs to represent the gating variables of that model.
A number of ionic cell models are currently supported by the solver including:
Phenomological cell models are also supported:
It is important to ensure that the units of the voltage and currents from the cell model are consistent with the units expected by the tissue level solver (monodomain/bidomain). We will show as an example the Courtemanche, Ramirez, Nattel, 1998 human atrial model.
The monodomain equation:
χ![[ ]
∂Vm-
Cm ∂t + Jion](user-guide49x.png) | = ∇⋅ (σ∇V m) |