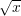3.6 Analytic Expressions
This section discusses particulars related to analytic expressions appearing in Nektar++.
Analytic expressions in Nektar++ are used to describe spatially or temporally varying
properties, for example
- velocity profiles on a boundary
- some reference functions (e.g. exact solutions)
which can be retrieved in the solver code.
Analytic expressions appear as the content of VALUE attribute of
- boundary condition type tags within
<REGION> subsection of
<BOUNDARYCONDITIONS>, e.g. <D>, <N> etc.
- expression declaration tag
<E> within <FUNCTION> subsection.
The tags above declare analytic expressions as well as link them to one of the field variables
declared in <EXPANSIONS> section. For example, the declaration
1 <D VAR="u" VALUE="sin(PI*x)*cos(PI*y)" />
registers expression sin(πx)cos(πy) as a Dirichlet boundary constraint associated with field
variable u.
Enforcing the same velocity profile at multiple boundary regions and/or field variables results
in repeated re-declarations of a corresponding analytic expression. Currently one cannot
directly link a boundary condition declaration with an analytic expression uniquely specified
somewhere else, e.g. in the <FUNCTION> subsection. However this duplication does not affect an
overall computational performance.
3.6.1 Variables and coordinate systems
Declarations of analytic expressions are formulated in terms of problem space-time
coordinates. The library code makes a number of assumptions to variable names and their
order of appearance in the declarations. This section describes these assumptions.
Internally, the library uses 3D global coordinate space regardless of problem dimension.
Internal global coordinate system has natural basis (1,0,0),(0,1,0),(0,0,1) with coordinates
”’x”’,”’y”’ and ”’z”’. In other words, variables ”’x”’,”’y”’ and ”’z”’ are considered to be first,
second and third coordinates of a point (”’x”’,”’y”’,”’z”’).
Declarations of problem spatial variables do not exist in the current XML file format. Even
though field variables are declarable as in the following code snippet,
1 <VARIABLES>
2 <V ID="0"> u </V>
3 <V ID="1"> v </V>
4 </VARIABLES>
there are no analogous tags for space variables. However an attribute SPACE of <GEOMETRY>
section tag declares the dimension of problem space. For example,
1 <GEOMETRY DIM="1" SPACE="2"> ...
2 </GEOMETRY>
specifies 1D flow within 2D problem space. The number of spatial variables presented in
expression declaration should match space dimension declared via <GEOMETRY> section
tag.
The library assumes the problem space also has natural basis and spatial coordinates have
names ”’x”’,”’y”’ and”’z”’.
Problem space is naturally embedded into the global coordinate space: each point of
- 1D problem space with coordinate x is represented by 3D point (x,0,0) in the global
coordinate system;
- 2D problem space with coordinates (x,y) is represented by 3D point (x,y,0) in the
global coordinate system;
- 3D problem space with coordinates (x,y,z) has the same coordinates in the global
space coordinates.
Currently, there is no way to describe rotations and translations of problem space relative to
the global coordinate system.
The list of variables allowed in analytic expressions depends on the problem dimension:
- For 1D problem analytic expressions must make use of variable ”’x”’ only;
- For 2D problem analytic expressions should make use of variables ”’x”’ and ”’y”’.
- 3D problems may use variables ”’x”’, ”’y”’ and ”’z”’ in their analytic expressions.
Violation of these constraints yields unpredictable results of expression evaluation. The
current implementation assigns magic value -9999 to each dimensionally excessive spacial
variable appearing in analytic expressions. For example, the following declaration
1 <GEOMETRY DIM="2" SPACE="2"> ...
2 </GEOMETRY> ...
3 <CONDITIONS> ...
4 <BOUNDARYCONDITIONS>
5 <REGION REF="0">
6 <D VAR="u" VALUE="x+y+z" /> <D VAR="v" VALUE="sin(PI*x)*cos(PI*y)" />
7 </REGION>
8 </BOUNDARYCONDITIONS>
9 ...
10 </CONDITIONS>
results in expression x + y + z being evaluated at spatial points (xi,yi,-9999) where
xi and yi are the spacial coordinates of boundary degrees of freedom. However,
the library behaviour under this constraint violation may change at later stages
of development (e.g., magic constant 0 may be chosen) and should be considered
unpredictable.
Another example of unpredictable behaviour corresponds to wrong ordering of variables:
1 <GEOMETRY DIM="1" SPACE="1"> ...
2 </GEOMETRY> ...
3 <CONDITIONS> ...
4 <BOUNDARYCONDITIONS>
5 <REGION REF="0">
6 <D VAR="u" VALUE="sin(y)" />
7 </REGION>
8 </BOUNDARYCONDITIONS>
9 ...
10 </CONDITIONS>
Here one declares 1D problem, so Nektar++ library assumes spacial variable is ”’x”’. At the
same time, an expression sin(y) is perfectly valid on its own, but since it does not depend on
”’x”’, it will be evaluated to constant sin(-9999) regardless of degree of freedom under
consideration.
3.6.1.1 Time dependence
Variable ”’t”’ represents time dependence within analytic expressions. The boundary condition
declarations need to add an additional property USERDEFINEDTYPE="TimeDependent" in order
to flag time dependency to the library.
3.6.1.2 Syntax of analytic expressions
Analytic expressions are formed of
- brackets (). Bracketing structure must be balanced.
- real numbers: every representation is allowed that is correct for
boost::lexical_cast<double>(),
e.g.
- mathematical constants
- parameters: alphanumeric names with underscores, e.g.
GAMMA_123, GaM123_45a_,
_gamma123 are perfectly acceptable parameter names. However parameter name cannot start
with a numeral. Parameters must be defined with <PARAMETERS>...</PARAMETERS>.
Parameters play the role of constants that may change their values in between of
expression evaluations.
- variables (i.e.,
x, y, z and t)
- unary minus operator (e.g.
-x)
- binary arithmetic operators
+, -, *, /, ^ Powering operator allows using real
exponents (it is implemented with std::pow() function)
- boolean comparison operations
<, <=, >, >=, == evaluate their sub-expressions to real
values 0.0 or 1.0.
- mathematical functions of one or two arguments:
| Identifier | Meaning |
abs(x) | absolute value |x| |
asin(x) | inverse sine arcsin x |
acos(x) | inverse cosine arccosx |
ang(x,y) | computes polar coordinate θ = arctan(y∕x) from (x,y) |
atan(x) | inverse tangent arctan x |
atan2(y,x) | inverse tangent function (used in polar transformations) |
ceil(x) | round up to nearest integer ⌈x⌉ |
cos(x) | cosine cosx |
cosh(x) | hyperbolic cosine cosh x |
exp(x) | exponential ex |
fabs(x) | absolute value (equivalent to abs) |
floor(x) | rounding down ⌊x⌋ |
log(x) | logarithm base e, ln x = log x |
log10(x) | logarithm base 10, log 10x |
rad(x,y) | computes polar coordinate r = 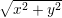 from (x,y) from (x,y) |
sin(x) | sine sin x |
sinh(x) | hyperbolic sine sinh x |
sqrt(x) | square root 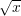 |
tan(x) | tangent tan x |
tanh(x) | hyperbolic tangent tanh x |
| |
These functions are implemented by means of the cmath library:
http://www.cplusplus.com/reference/clibrary/cmath/. Underlying data type is
double at each stage of expression evaluation. As consequence, complex-valued
expressions (e.g. (-2)0.123) get value nan (not a number). The operator ^
is implemented via call to std::pow() function and accepts arbitrary real
exponents.
- random noise generation functions. Currently implemented is
awgn(sigma) - Gaussian
Noise generator, where σ is the variance of normal distribution with zero mean.
Implemented using the boost::mt19937 random number generator with boost variate
generators (see http://www.boost.org/libs/random)
3.6.1.3 Examples
Some straightforward examples include
- Basic arithmetic operators:
0.5*0.3164/(3000^0.25)
- Simple polynomial functions:
y*(1-y)
- Use of values defined in
PARAMETERS section: -2*Kinvis*(x-1)
- More complex expressions involving trigonometric functions, parameters and
constants:
(LAMBDA/2/PI)*exp(LAMBDA*x)*sin(2*PI*y)
- Boolean operators for multi-domain functions:
(y<0)*sin(y) + (y>=0)*y
3.6.2 Performance considerations
Processing analytic expressions is split into two stages:
- parsing with pre-evaluation of constant sub-expressions,
- evaluation to a number.
Parsing of analytic expressions with their partial evaluation take place at the time of setting
the run up (reading an XML file). Each analytic expression, after being pre-processed, is
stored internally and quickly retrieved when it turns to evaluation at given spatial-time
point(s). This allows to perform evaluation of expressions at a large number of spacial points
with minimal setup costs.
3.6.2.1 Pre-evaluation details
Partial evaluation of all constant sub-expressions makes no sense in using derived constants
from table above. This means, either make use of pre-defined constant LN10^2 or
straightforward expression log10(2)^2 results in constant 5.3018981104783980105 being
stored internally after pre-processing. The rules of pre-evaluation are as follows:
- constants, numbers and their combinations with arithmetic, analytic and
comparison operators are pre-evaluated,
- appearance of a variable or parameter at any recursion level stops pre-evaluation of
all upper level operations (but doesn’t stop pre-evaluation of independent parallel
sub-expressions).
For example, declaration
1 <D VAR="u" VALUE="exp(-x*sin(PI*(sqrt(2)+sqrt(3))/2)*y )" />
results in expression exp(-x*(-0.97372300937516503167)*y ) being stored internally:
sub-expression sin(PI*(sqrt(2)+sqrt(3))/2) is evaluated to constant but appearance of x
and y variables stops further pre-evaluation.
Grouping predefined constants and numbers together helps. Its useful to put brackets
to be sure your constants do not run out and become factors of some variables or
parameters.
Expression evaluator does not do any clever simplifications of input expressions, which is clear
from example above (there is no point in double negation). The following subsection addresses
the simplification strategy.
3.6.2.2 Preparing analytic expression
The total evaluation cost depends on the overall number of operations. Since evaluator is not
making simplifications, it worth trying to minimise the total number of operations in input
expressions manually.
Some operations are more computationally expensive than others. In an order of increasing
complexity:
+, -, <, >, <=, >=, ==,
*, /, abs, fabs, ceil, floor,
^, sqrt, exp, log, log10, sin, cos, tan, sinh, cosh, tanh, asin,
acos, atan.
For example,
x*x is faster than x^2 — it is one double multiplication vs generic calculation of
arbitrary power with real exponents.
(x+sin(y))^2 is faster than (x+sin(y))*(x+sin(y)) - sine is an expensive
operation. It is cheaper to square complicated expression rather than compute it
twice and add one multiplication.
- An expression
exp(-41*( (x+(0.3*cos(2*PI*t)))^2 + (0.3*sin(2*PI*t))^2
)) makes use of 5 expensive operations (exp, sin, cos and power ^ twice) while an
equivalent expression exp(-41*( x*x+0.6*x*cos(2*PI*t) + 0.09 )) uses only
2 expensive operations.
If any simplifying identity applies to input expression, it may worth applying it,
provided it minimises the complexity of evaluation. Computer algebra systems may
help.
3.6.2.3 Vectorized evaluation
Expression evaluator is able to calculate an expression for either given point (its space-time
coordinates) or given array of points (arrays of their space-time coordinates, it uses SoA).
Vectorized evaluation is faster then sequential due to a better data access pattern. Some
expressions give measurable speedup factor 4.6. Therefore, if you are creating your own solver,
it worth making vectorized calls.
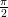
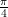

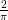
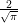
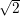
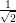
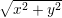 from (x,y)
from (x,y)