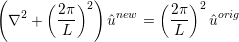
FieldConvert allows the user to manipulate the Nektar++ output binary files (.chk and .fld)
by using the flag -m (which stands for module).. Specifically, FieldConvert has these additional
functionalities
C0Projection: Computes the C0 projection of a given output file;
QCriterion: Computes the Q-Criterion for a given output file;
addFld: Sum two .fld files;
concatenate: Concatenate a Nektar++ binary output (.chk or .fld) field file into
single file;
equispacedoutput: Write data as equi-spaced output using simplices to represent
the data for connecting points;
extract: Extract a boundary field;
homplane: Extract a plane from 3DH1D expansions;
innerproduct: take the inner product between one or a series of fields with another
field (or series of fields).
interpfield: Interpolates one field to another, requires fromxml, fromfld to be
defined;
interppointdatatofld: Interpolates given discrete data using a finite difference
approximation to a fld file given an xml file;
interppoints: Interpolates a set of points to another, requires fromfld and
fromxml to be defined, a line or plane of points can be defined;
isocontour: Extract an isocontour of “fieldid” variable and at value “fieldvalue”.
Optionally “fieldstr” can be specified for a string defiition or “smooth” for
smoothing;
jacobianenergy: Shows high frequency energy of Jacobian;
meanmode: Extract mean mode (plane zero) of 3DH1D expansions;
pointdatatofld: Given discrete data at quadrature points project them onto an
expansion basis and output fld file;
printfldnorms: Print L2 and LInf norms to stdout;
scalargrad: Computes scalar gradient field;
scaleinputfld: Rescale input field by a constant factor;
shear: Computes time-averaged shear stress metrics: TAWSS, OSI, transWSS,
TAAFI, TACFI, WSSG;
surfdistance: Computes height of a prismatic boundary layer mesh and projects
onto the surface (for e.g. y+ calculation).
vorticity: Computes the vorticity field.
wss: Computes wall shear stress field.The module list above can be seen by running the command
In the following we will detail the usage of each module.
To smooth the data of a given .fld file one can use the C0Projection module of FieldConvert
where the file test-C0Proj.fld can be processed in a similar way as described in section 5.1
to visualise the result either in Tecplot, Paraview or VisIt.
The option localtoglobalmap will do a global gather of the coefficients and then scatter
them back to the local elements. This will replace the coefficients shared between two elements
with the coefficients of one of the elements (most likely the one with the highest id). Although
not a formal projection it does not require any matrix inverse and so is very cheap to
perform.
The option usexmlbcs will enforce the boundary conditions specified in the input xml
file.
The option helmsmoothing=L will perform a Helmholtz smoothing projection of the
form
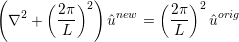
which can be interpreted in a Fourier sense as smoothing the original coefficients using a low pass filter of the form
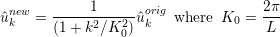
and so L is the length scale below which the coefficients values are halved or more. Since this form of the Helmholtz operator is not possitive definite, currently a direct solver is necessary and so this smoother is mainly of use in two-dimensions.
To perform the Q-criterion calculation and obtain an output data containing the Q-criterion solution, the user can run
where the file test-QCrit.fld can be processed in a similar way as described in section 5.1 to
visualise the result either in Tecplot, Paraview or VisIt.
To sum two .fld files one can use the addFld module of FieldConvert
In this case we use it in conjunction with the command scale which multiply the values of a
given .fld file by a constant value. file1.fld is the file multiplied by value, file1.xml is the
associated session file, file2.fld is the .fld file which is summed to file1.fld and finally
file3.fld is the output which contain the sum of the two .fld files. file3.fld can be
processed in a similar way as described in section 5.1 to visualise the result either in Tecplot,
Paraview or VisIt.
To concatenate file1.fld and file2.fld into file-conc.fld one can run the following
command
where the file file-conc.fld can be processed in a similar way as described in section 5.1 to
visualise the result either in Tecplot, Paraview or VisIt.
This module interpolates the output data to an truly equispaced set of points (not equispaced along the collapsed coordinate system). Therefore a tetrahedron is represented by a tetrahedral number of poinst. This produces much smaller output files. The points are then connected together by simplices (triangles and tetrahedrons).
or
The boundary region of a domain can be extracted from the output data using the following command line
The option bnd specifies which boundary region to extract. Note this is different to NekMesh
where the parameter surf is specified and corresponds to composites rather boundaries. If bnd
is not provided, all boundaries are extracted to different fields. The fldtoboundary is an
optional command argument which copies the expansion of test.fld into the boundary region
before outputting the .fld file. This option is on by default. If it turned off using
fldtoboundary=0 the extraction will only evaluate the boundary condition from the xml file.
The output will be placed in test-boundary-b2.fld. If more than one boundary region is
specified the extension -b0.fld, -b1.fld etc will be outputted. To process this file you will
need an xml file of the same region. This can be generated using the command:
The surface to be extracted in this command is the composite number and so needs to correspond to the boundary region of interest. Finally to process the surface file one can use
This will obviously generate a Tecplot output if a .dat file is specified as last argument. A .vtu extension will produce a Paraview or VisIt output.
To compute the spatial gradients of all fields one can run the following command
where the file file-grad.fld can be processed in a similar way as described in section 5.1 to
visualise the result either in Tecplot, Paraview or VisIt.
To obtain a 2D expansion containing one of the planes of a 3DH1D field file, use the command:
If the option wavespace is used, the Fourier coefficients corresponding to planeid are
obtained. The command in this case is:
The output file file-plane.fld can be processed in a similar way as described in section 5.1
to visualise it either in Tecplot or in Paraview.
You can take the inner product of one field with another field using the following command:
This command will load the file1.fld and file2.fld assuming they both are spatially
defined by files.xml and determine the inner product of these fields. The input option
fromfld must therefore be specified in this module.
Optional arguments for this module are fields which allow you to specify the fields that you
wish to use for the inner product, i.e.
will only take the inner product between the variables 0,1 and 2 in the two fields files. The default is to take the inner product between all fields provided.
Additional options include multifldids and allfromflds which allow for a series of fields to
be evaluated in the following manner:
will take the inner product between a file names field1_0.fld, field1_1.fld, field1_2.fld and field1_3.fld with respect to field2.fld.
Analogously including the options allfromflds, i.e.
Will take the inner product of all the from fields, i.e. field1_0.fld,field1_1.fld,field1_2.fld and field1_3.fld with respect to each other. This option essentially ignores file2.fld. Only the unique inner products are evaluated so if four from fields are given only the related trianuglar number 4 × 5∕2 = 10 of inner products are evaluated.
This option can be run in parallel.
To interpolate one field to another, one can use the following command:
This command will interpolate the field defined by file1.xml and file1.fld to the new
mesh defined in file2.xml and output it to file2.fld. The fromxml and fromfld must be
specified in this module. In addition there are two optional arguments clamptolowervalue
and clamptouppervalue which clamp the interpolation between these two values. Their
default values are -10,000,000 and 10,000,000.
To interpolate discrete point data to a field, use the interppointdatatofld module:
This command will interpolate the data from file1.pts to the mesh and expansions defined
in file1.xml and output the field to file1.fld. The file file.pts is of the form:
where DIM="1" FIELDS="a,b,c specifies that the field is one-dimensional and contains three
variables, a, b, and c. Each line defines a point, while the first column contains its
x-coordinate, the second one contains the a-values, the third the b-values and so on. In case of
n-dimensional data, the n coordinates are specified in the first n columns accordingly. In order
to interpolate 1D data to a nD field, specify the matching coordinate in the output field using
the interpcoord argument:
This will interpolate the 1D scattered point data from 1D-file1.pts to the y-coordinate of
the 3D mesh defined in 3D-file1.xml. The resulting field will have constant values along the
x and z coordinates. For 1D Interpolation, the module implements a quadratic scheme
and automatically falls back to a linear method if only two data points are given.
A modified inverse distance method is used for 2D and 3D interpolation. Linear
and quadratic interpolation require the data points in the .pts-file to be sorted by
their location in ascending order. The Inverse Distance implementation has no such
requirement.
You can interpolate one field to a series of given points using the following command:
This command will interpolate the field defined by file1.xml and file1.fld to the points
defined in file2.pts and output it to file2.dat. The fromxml and fromfld must be
specified in this module. The format of the file file2.pts is of the same form as for the
interppointdatatofld module:
There are three optional arguments clamptolowervalue, clamptouppervalue and
defaultvalue the first two clamp the interpolation between these two values and the third
defines the default value to be used if the point is outside the domain. Their default values are
-10,000,000, 10,000,000 and 0.
In addition, instead of specifying the file file2.pts, a module list of the form
can be specified where npts is the number of equispaced points between (x0,y0) to (x1,y1)
which can also be used in 3D by specifying (x0,y0,z0) to (x1,y1,z1).
An extraction of a plane of points can also be specified by
where npts1,npts2 is the number of equispaced points in each direction and (x0,y0,z0),
(x1,y1,z1), (x2,y2,z2) and (x3,y3,z3) define the plane of points specified in a clockwise or
anticlockwise direction.
In addition an extraction of a box of points can also be specified by
where npts1,npts2,npts3 is the number of equispaced points in each direction
and (xmin,ymin,zmin) and (xmax,ymax,zmax3) define the limits of the box of
points.
For the plane and box interpolation there is an additional optional argument cp=p0,q which
adds to the interpolated fields the value of cp = (p-p0)∕q and cp0 = (p-p0 + 0.5u2)∕q where
p0 is a reference pressure and q is the free stream dynamics pressure. If the input does not
contain a field “p” or a velocity field “u,v,w” then cp and cp0 are not evaluated accordingly
Extract an isocontour from a field file. This option automatically take the field to an
equispaced distribution of points connected by linear simplicies of triangles or tetrahedrons.
The linear simplices are then inspected to extract the isocontour of interest. To specify the
field fieldid can be provided giving the id of the field of interest and fieldvalue provides
the value of the isocontour to be extracted.
Alternatively fieldstr=”u+v” can be specified to calculate the field u2 and extract its
isocontour. You can also specify fieldname=”UplusV” to define the name of the isocontour in
the .dat file, i.e.
Optionally smooth can be specified to smooth the isocontour with default values
smoothnegdiffusion=0.495, smoothnegdiffusion=0.5 and smoothiter=100. This option
typically should be used wiht the globalcondense option which removes multiply defined
verties from the simplex definition which arise as isocontour are generated element by element.
The smooth option preivously automatically called the globalcondense option but this has
been depracated since it is now possible to read isocontour files directly and so it is useful to
have these as separate options.
In addition to the smooth or globalcondense options you can specify removesmallcontour=100
which will remove separate isocontours of less than 100 triangles.
The option topmodes can be used to specify the number of top modes to keep.
The output file jacenergy.fld can be processed in a similar way as described in section 5.1 to
visualise the result either in Tecplot, Paraview or VisIt.
To obtain a 2D expansion containing the mean mode (plane zero in Fourier space) of a 3DH1D field file, use the command:
The output file file-mean.fld can be processed in a similar way as described in section 5.1 to
visualise the result either in Tecplot or in Paraview or VisIt.
To project a series of points given at the same quadrature distribution as the .xml file and write out a .fld file use the pointdatatofld module:
This command will read in the points provided in the file.pts and assume these are
given at the same quadrature distribution as the mesh and expansions defined in
file.xml and output the field to file.fld. If the points do not match an error will be
dumped.
The file file.pts which is assumed to be given by an interpolation from another source is of
the form:
where DIM="3" FIELDS="p specifies that the field is three-dimensional and contains one
variable, p. Each line defines a point, the first, second, and third columns contains the
x,y,z-coordinate and subsequent columns contain the field values, in this case the p-value So
in the general case of n-dimensional data, the n coordinates are specified in the first n columns
accordingly followed by the field data.
The default argument is to use the equipapced (but potentially collapsed) coordinates which can be obtained from the command.
In this case the pointdatatofld module shoudl be used without the –noequispaced
option. However this can lead to problems when peforming an elemental forward
projection/transform since the mass matrix in a deformed element can be singular
as the equispaced points do not have a sufficiently accurate quadrature rule that
spans the polynomial space. Therefore it is adviseable to use the set of points given
by
which produces a set of points at the gaussian collapsed coordinates. In this case one must also
use the –noequispaced option when projecting to a field.
Finally the option setnantovalue=0 can also be used which sets any nan values in the
interpolation to zero or any specified value in this option.
This module does not create an output file which is reinforced by the out.stdout option. The L2 and LInf norms for each field variable are then printed to the stdout.
The scalar gradient of a field is computed by running:
The option bnd specifies which boundary region to extract. Note this is different to NekMesh
where the parameter surf is specified and corresponds to composites rather boundaries. If bnd
is not provided, all boundaries are extracted to different fields. To process this file you will
need an xml file of the same region.
To scale a .fld file by a given scalar quantity, the user can run:
The argument scale=value rescales of a factor value test.fld by the factor value. The
output file file-conc.fld can be processed in a similar way as described in section 5.1 to
visualise the result either in Tecplot, Paraview or VisIt.
Time-dependent wall shear stress derived metrics relevant to cardiovascular fluid dynamics research can be computed using this module. They are
To compute these, the user can run:
The argument N and fromfld are compulsory arguments that respectively define the number
of fld files corresponding to the number of discrete equispaced time-steps, and the first fld
file which should have the form of test_id_b0.fld where the first underscore in the name
marks the starting time-step file ID.
The input .fld files are the outputs of the wss module. If they do not contain the surface
normals (an optional output of the wss modle), then the shear module will not compute the
last metric, |WSSG|.
The surface distance module computes the height of a prismatic boundary layer and projects
this value onto the surface of the boundary, in a similar fashion to the extract
module. In conjunction with a mesh of the surface, which can be obtained with
NekMesh, and a value of the average wall shear stress, one potential application
of this module is to determine the distribution of y+ grid spacings for turbulence
calculations.
To compute the height of the prismatic layer connected to boundary region 3, the user can issue the command:
Note that no .fld file is required, since the mesh is the only input required in order to
calculate the element height. This produces a file output_b3.fld, which can be visualised
with the appropriate surface mesh from NekMesh.
To perform the vorticity calculation and obtain an output data containing the vorticity solution, the user can run
where the file test-vort.fld can be processed in a similar way as described in section
5.1.
To obtain the wall shear stres vector and magnitude, the user can run:
The option bnd specifies which boundary region to extract. Note this is different to NekMesh
where the parameter surf is specified and corresponds to composites rather boundaries. If bnd
is not provided, all boundaries are extracted to different fields. The addnormals is an optional
command argument which, when turned on, outputs the normal vector of the extracted
boundary region as well as the shear stress vector and magnitude. This option is
off by default. To process the output file(s) you will need an xml file of the same
region.
FieldConvert has support for two modules that can be used in conjunction with the linear elastic solver, as shown in chapter 11. To do this, FieldConvert has an XML output module, in addition to the Tecplot and VTK formats.
The deform module, which takes no options, takes a displacement field and applies it to the
geometry, producing a deformed mesh:
The displacement module is designed to create a boundary condition field file.
Its intended use is for mesh generation purposes. It can be used to calculate the
displacement between the linear mesh and a high-order surface, and then produce a fld file,
prescribing the displacement at the boundary, that can be used in the linear elasticity
solver.
Presently the process is somewhat convoluted and must be used in conjunction with NekMesh
to create the surface file. However the bash input below describes the procedure. Assume the
high-order mesh is in a file called mesh.xml, the linear mesh is mesh-linear.xml that can be
generated by removing the CURVED section from mesh.xml, and that we are interested in the
surface with ID 123.