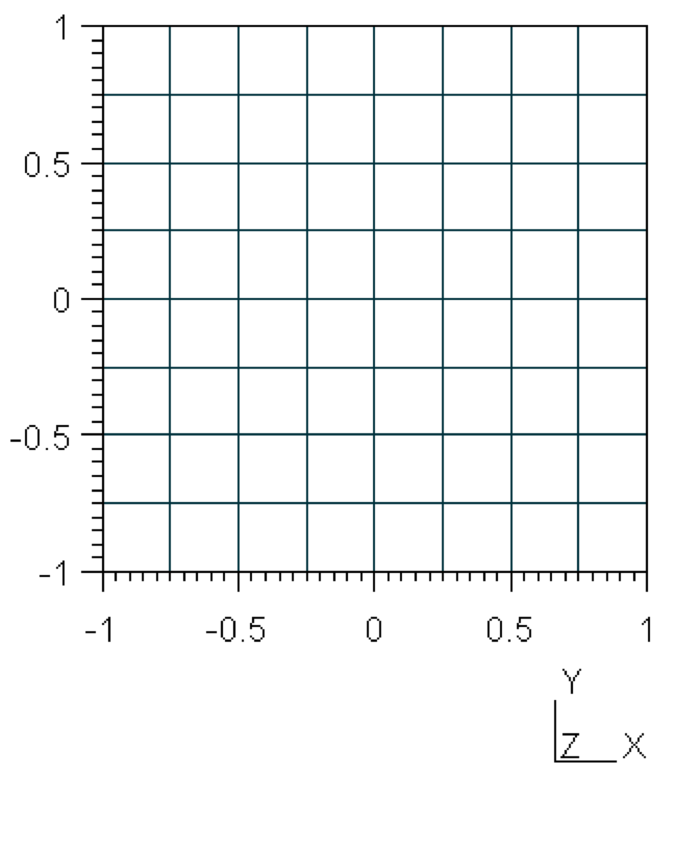
In this section we explain how to set up a simple simulation of aeroacoustics in Nektar++. We will study the propagation of an acoustic wave in the simple case where the base flow is ui = 0,p = p∞ = 106,ρ = ρ0 = 1.204. The geometry consists of 64 quadrilateral elements, as shown in Fig. 7.1.

We require a discontinuous Galerkin projection and use an explicit fourth-order Runge-Kutta time integration scheme. We therefore set the following solver information:
To maintain numerical stability we must use a small time-step. The total simulation time is 150 time units. Finally, we set the density, heat ratio and ambient pressure.
Let us note that to solve efficiently this problem a discontinuous Garlerkin approach was used. The system is excited via the initial conditions putting a Gaussian pulse for pulse fluctuations. Finally, it is necessary to specify the base flow and the eventual source terms using the following functions:
Fig. 7.2 shows the pressure profile at different time steps, showing the acoustic propagation.
It is possible to show the profile of the pressure perturbations with respect to the spatial coordinate. The pressure fluctuations, that are concentrated in a specific locations at the beginning (as specified by the initial conditions), propagate with time and for sufficiently large time the decay is exponential as predicted by literature [10].