Figure 10.3: Velocity profiles for the Kovasznay Flow (2D).
This example demonstrates the use of the velocity correction o solve the 2D Kovasznay flow at Reynolds number Re = 40. In the following we will numerically solve for the two dimensional velocity and pressure fields with steady boundary conditions.
The input for this example is given in the example file KovaFlow_m8.xml. The mesh consists
of 12 quadrilateral elements.
We will use a 7th-order polynomial expansions (N = 8 modes) using the modified Legendre basis and therefore require the following expansion definition.
We next specify the solver information for our problem. In particular, we select the velocity correction scheme formulation, using a continuous Galerkin projection. For this scheme, an implicit-explicit ime-integration scheme must be used and we choose one of second order.
The key parameters are listed below. Since the problem is unsteady we prescribe the time step
and the total number of time steps. We also know the required Reynolds number, but we must
prescribe the kinematic viscosity to the solver. We first define a dummy parameter for the
Reynolds number, and then define the kinematic viscosity as the inverse of this. The value of λ
is used when defining the boundary conditions and exact solution. Note that PI is a
pre-defined constant.
We choose to impose a mixture of boundary condition types as defined below.
Initial conditions are obtained from the file KovaFlow_m8.rst, which is a Nektar++ field file.
This is the output of an earlier simulation, renamed with the extension rst to avoid being
overwritten, and is used in this case to reduce the integration time necessary to obtain the
steady flow.
Note the use of the F tag to indicate the use of a file. In contrast, the exact solution is
prescribed using analytic expressions which requires the use of the E tag.
Launch the simulation using the following command
After completing the prescribed 100 time-steps, the difference between the computed solution and the exact solution will be displayed. The actual mantissas may vary slightly, but the overall magnitude should be as shown.
The output of the simulation is written to KovaFlow_m8.fld. This can be visualised by
converting it to a visualisation format. For example, to use ParaView, convert the output into
VTK format using the tility.
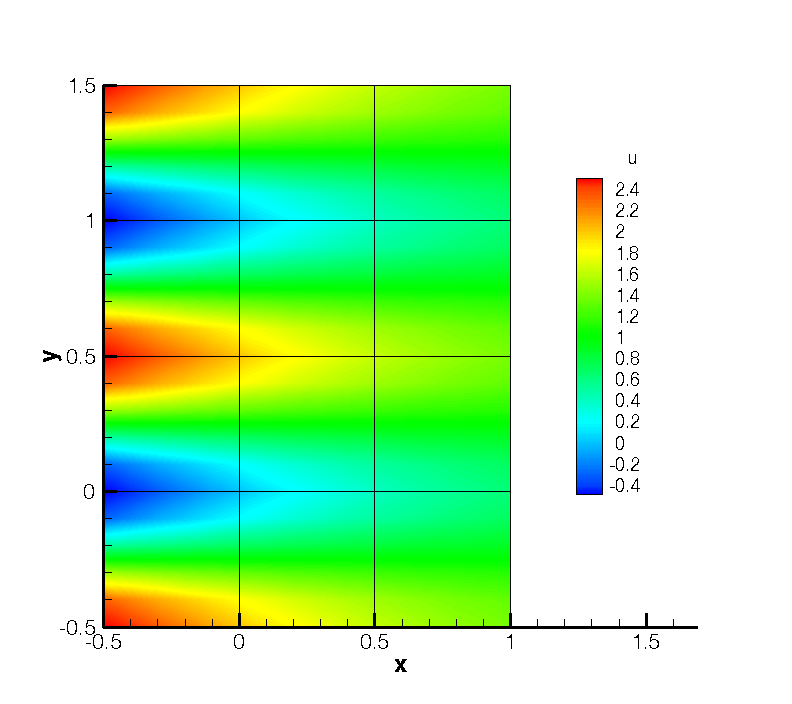
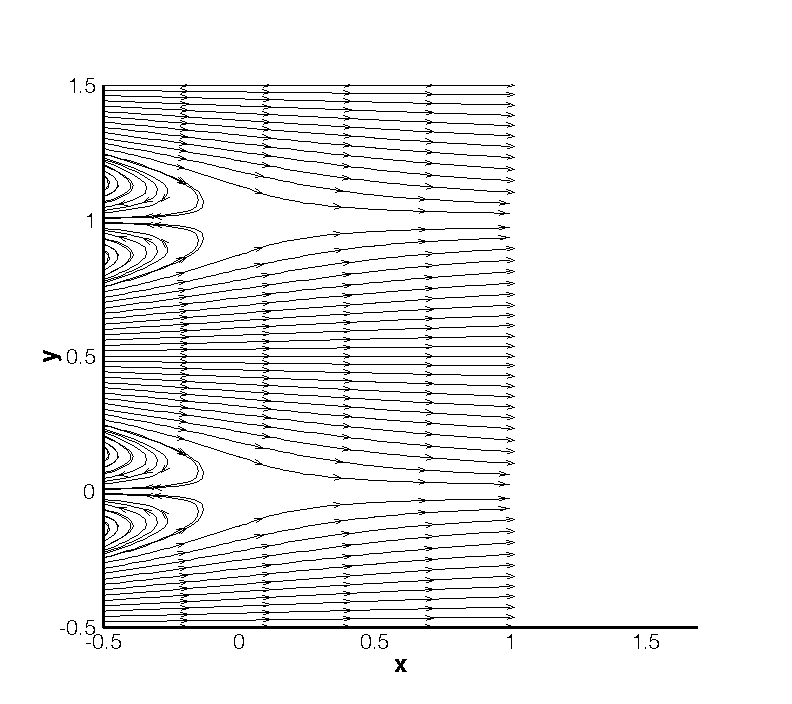
The result should look similar to that shown in Figure 10.3.
In this example, we solve the same case of 2D Kovasznay flow on severely-truncated computational domain but using a high-order outflow boundary condition, which is much more accurate and robust for unbounded flows [9]. The solver information and parameters used here are similar to the previous one. What only we need to modify in the input file is just the boundary condition type upon the outlet region shown as below
We note that in this example the “VALUE” property is set based on the analytic solution but this is not typically known and so often a VALUE of zero will be specified.
Instead of loading an initial condition from a specified file, we initialized the flow fields in this example by using following expressions
We then launch the simulation by the same solver as that in the previous example
The solution with errors displayed as below
The physical solution visualized in velocity profiles is also illustrated in Figure 10.4.
In this example, we instead compute the steadhy Kovasznay Oseen flow using the direct solver. In contrast to the velocity correction scheme in which we time-step the solution to the final time, the direct solver computes the solution with a single solve.
We can begin with the same input file as for the previous example, but with the
following modifications. For reference, the modified version is provided in the example
Oseen_m8.xml.
In the solver information, we must instead select the Steady-Oseen equation type and choose to use the coupled linearised Navier-Stokes
p in the session. In particular, it should be
removed from the EXPANSIONS, VARIABLES, BOUNDARYCONDITIONS and FUNCTIONS sections of
the file.
Instead of loading an initial condition from file, we can simply prescribe a zero field.
We must also provide an advection velocity.
Run the simulation using
The resulting flow field should match the solution from the previous example.
In this example, we will simulate the flow through a channel at Reynolds number 1 with fixed boundary conditions.
The input file for this example is given in ChanFlow_m3_SKS.xml. The geometry is a square
channel with height and length D = 1, discretised using four quadrilateral elements. We use a
quadratic expansion order, which is sufficient to capture the quadratic flow profile. In this
example, we choose to use the skew-symmetric form of the advection term. This is chosen in
the solver information section:
A first-order time integration scheme is used and we set the time-step and number of time integration steps in the parameters section. We also prescribe the kinematic viscosity ν = 1∕Re = 1.
Boundary conditions are defined on the walls (region 0) and at the inflow (regions 1) as Dirichlet for the velocity field and as high-order for the pressure. At the outflow the velocity is left free using Neumann boundary conditions and the pressure is pinned to zero.
Initial conditions are set to zero. The exact solution is a parabolic profile with a pressure gradient dependent on the Reynolds number. This is defined to allow verification of the calculation.
The error in the solution should be displayed and be close to machine precision
The solution should look similar to that shown in Figure 10.5.
We now solve the incompressible Navier-Stokes equations on a three-dimensional domain. In particular, we solver the three-dimensional equivalent of the previous example. We will also solve the problem in parallel.
The input file for this example is given in Tet_channel_m8_par.xml. In this example we use
tetrahedral elements, indicated by the A element tags in the geometry section. All dimensions
have length D = 1. We will use a 7th-order polynomial expansion. Since we now have three
dimensions, and therefore three velocity components, the expansions section is now
The solver information and parameters are similar to the previous example. Boundary conditions must now be defined on the six faces of the domain. Flow is prescribed in the z-direction through imposing a Poiseulle profile on the inlet and side walls. The outlet is zero-Neumann and top and bottom faces impose zero-Dirichlet conditions.
Initial conditions and exact solutions are also prescribed.
To run the solver in parallel, we use the mpirun command.
The expected results are shown in Figure 10.6.
For domains where at least one direction is geometrically homogeneous, a more efficient discretisation is to use a pure spectral discretisation, such as a Fourier expansion, in these directions. We use this approach to solve the same problem as in the previous example. We reuse the two-dimensional spectral/hp element mesh from the nd couple this with a Fourier expansion in the third component.
The input file for this example is ChanFlow_3DH1D_MVM.xml. We indicate that we are coupling
the spectral/hp element domain with a pure spectral expansion using the following solver
information
We must also specify parameters to describe the particular spectral expansion
The parameter HomModesZ specifies the number of Fourier modes to use in the homogeneous
direction. The LZ parameter specifies the physical length of the domain in that
direction.
As with the the spectral/hp element mesh consists of four quadrilateral elements with a second-order polynomial expansion. Since our domain is three-dimensional we have to now include the third velocity component
The remaining parameters and solver information is similar to previous examples.
Boundary conditions are specified as for the two-dimensional case (except with the addition of the third velocity component) since the side walls are now implicitly periodic. The initial conditions and exact solution are prescribed as for the fully three-dimensional case.
The results can be post-processed and should match those of the fully three-dimensional case as shown in Figure 10.6.
In this example we model turbulence in a three-dimensional square channel at a Reynolds number of 2000.
The input file for this example is TurbChFl_3DH1D.xml. The geometry makes used of the
homogeneous extension discussed in the previous example. The channel has height D = 2 and
length L = 4π and is discretised using quadratic quadrilateral elements in the spectral/hp
element plane and a Fourier basis in the third coordinate direction. The elements are
non-uniformly distributed so as to best capture the flow features with fewest degrees of
freedom and is shown in Figure 10.7.
The spanwise length of the channel is set using the LZ parameter and discretised with 32
Fourier modes by setting the value of HomModesZ.
A second-order IMEX scheme is used for time-integration scheme is used with a time-step of 0.0001. The length of the simulation is 1 time-unit (10,000 steps).
Periodicity is naturally enforced in the spanwise direction, so boundary conditions need only
be provided for the upper and lower walls, inlet and outlet as denoted by the following
BOUNDARYREGIONS.
In this example, we will use a body force to drive the flow and so, in addition to the spanwise periodicity, enforce periodicity in the streamwise direction of the spectral/hp element mesh. This is achieved by imposing the following boundary conditions
Here, we use P to denote the boundary type is periodic, and the value in square brackets
denotes the boundary region to which the given boundary is periodic with. In this case regions
1 and 2 are denoted periodic with each other.
A streamwise plug-profile initial condition is prescribed such that u = 1 everywhere, except
the wall boundaries. The body force requires two components in the XML file. The first
specifies the type of forcing to apply and appears directly within the NEKTAR tag.
The second defines the BodyForce function which will be used and is located within the
CONDITIONS section,
To improve numerical stability, we also enable dealising of the advection term. This uses additional points to perform the quadrature and then truncates the higher-order terms when projecting back onto the polynomial space, thereby removing spurious oscillations. It is enabled by setting the solver information tag
This feature is only available when using the FFTW library is used, so we enable this using
To run the solver, we use the following command
The result after transition has occurred is illustrated in Figure 10.8.
In this example we simulate flow in a pipe at Reynolds number 3000 using a mixed spectral/hp element and Fourier discretisation. The Fourier expansion is used in the streamwise direction in this case and the spectral/hp elements are used to capture the circular cross-section.
The circular pipe has diameter D = 1, the 2D mesh is composed of 64 quadrilateral elements and the streamwise direction is discretised with 128 Fourier modes. An illustrative diagram of the discretisation is given in Figure 10.9.
The input file for this example is Pipe_turb.xml. We use 7th-order lagrange polynomials
through the Gauss-Lobatto-Legendre points for the quadrilateral expansions.
We set the Fourier options, as in the previous example, except using 128 modes and a length of 5 non-dimensional units. A small amplitude noise is also added to the initial condition, which is a plug profile, to help stimulate transition. Since the streamwise direction is the Fourier direction, we must necessarily use a body force to drive the flow.
In this example we will run the solver in parallel. Due to the large number of Fourier modes
and relatively few elements, it is more efficient to parallelise in the streamwise direction. We
can specify this by providing an additional flag to the solver, –npz. This indicates the number
of partitions in the z-coordinate. In this example, we will only run two processes. We
therefore would specify –npz 2 to ensure parallelisation only occurs in the Fourier
direction.
To improve the efficiency of the solver further, we would prefer to solve the Helmholtz problems within the spectral/hp element planes using a direct solver (since no parallelisation is necessary). The default when running in parallel is to use an iterative solver, so we explicitly specify the type of algorithm to use in the session file solver information:
The solver can now be run as follows
When the pipe transitions, the result should look similar to Figure 10.10.
The following example demonstrates the application of the incompressible Navier-Stokes solver using the Velocity Correction Scheme algorithm for modelling viscid Newtonian blood flow in a region of a rabbit descending thoracic aorta with intercostal branch pairs. Such studies are necessary to understand the effect local blood flow changes have on cardiovascular diseases such as atherosclerosis.
In the following we will numerically solve for the three dimensional velocity and pressure field for steady boundary conditions. The Reynolds number under consideration is 300, which is physiologically relevant.
Geometry
The geometry under consideration is a segment of a rabbit descending aorta with two pairs of intercostal arteries branching off. The inlet has a diameter D = 3.32mm.
In order to capture the physics of the flow in the boundary layer, a thin layer consisting of prismatic elements is created adjacent to the surface, and curved using spherigons. The interior consist of tetrahedral elements.
Input parameters
In this example we will use a fourth order polynomial expansion. There are two composites defined here since we have both prismatic and tetrahedral elements.
Since we are prescribing a Reynolds number of 300, and to simplify the problem definition, we
set the mean inlet velocity to 1, this allows us to define the kinematic viscosity as
ν =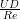 
= 
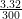= 1∕90.36.
For the purpose of this example a blunted inlet velocity profile has been prescribed. Ideally to obtain more significant results, the velocity profile at the inlet would be obtained from previous simulations on the complete rabbit aorta (including aortic root, aortic arch, and descending aorta with all 5 pairs of intercostal arteries), where a blunted profile at the aortic root is a better representation of reality.
Dirichlet boundary conditions are imposed for the velocity at the inlet, as well as on the wall to account for the no-slip condition. Neumann boundary conditions are imposed for the velocity field at the outlets where fully developed flow is imposed.
We can visualise the internal velocity field by applying a volume render filter in ParaView.
It is possible to visualise the wall shear stress distribution by running the FldAddWSS utility.
As a computationally efficient model, strip theory-based modeling technique has been proposed previously to predict vortex-induced vibration (VIV) for higher Reynolds number flows. In the strip theory-based model, the fluid flow solution is obtained on a series of 2D computational planes (also called as “strips”) along the riser’s axis direction. These strips then are coupled with each other through structural dynamic model of the riser, and then VIV response prediction is achieved by the strip-structure interactions.In the 2D strip theory, it is assumed that the flow is purely two-dimensional without spanwise correlation, which allows the problems to be split into various 2D planes. A consequence of 2D strip solution under this assumption is that it is unable to reflect the influence of spanwise wake turbulence on the structural dynamics. In order to overcome this shortcoming, we proposed a new module in the framework of Nektar++, in which a spanwise scale is locally allocated to each one of the strips, so that the spanwise velocity correlation is reconstructed in the flow field within each strips. In particular, this model lets the fluid domain to be divided in N strips with thickness ratio of Lz∕D and evenly distributed along the spanwise (z) direction. The gap between the neighboring strips, represented by Lg, satisfies relation Lc = N(Lz + Lg). Since the strip in this model has finite scale in the z-direction, we named it as finite strip to distinguish from traditional 2D strip plane. Next, the flow dynamics within each individual strips are modeled by viscous incompressible Navier-Stokes equations, while a tensioned beam model is employed to govern the dynamics of the flexible structures. In this example, we will show how to perform a finite-strip model to predict the vortex-induced vibration responses of flexible cables. Let us consider a vortex-induced vibration of a slender cable with an aspect ratio of Lz∕D=4π, which is immersed in uniform flows at Re=100.
The cable with a mass ratio (defined as the ratio of the total oscillating mass to the mass of
displaced fluid) of 1 has diameter D = 1, the 2D mesh is composed of 284 quadrilateral
elements. The spanwise direction is split in 16 strips with thickness ratio of Lc∕D=π/8 and
one pair of complex Fourier modes for each one of the strips. We will use a sixth order
polynomial expansion for the spectral element and the input file for this example is
CylFlow_HomoStrip.xml.
To use the finite strip routines we need just to insert a flag of "HomoStrip" in the solver
information as below, in addition, we need to specify the types of vibration and support ends
for the cables. In this case, the vibration type is specified as VALUE="CONSTRAINED", which
means that the cable’s vibration is constrained only in the crossflow direction. Other options
include VALUE="FREE" and "FORCED", respectively corresponding to the free vibrations in both
streamwise and crossflow directions and forced vibration by specified functions given in input
file. For the support ends of the cable, another option of VALUE="PINNED-PINNED" is available
for the simulations, which satisfies the condition of zero values of displacements on the support
ends.
All the simulation parameters are specified in the section as follows.
In this example we will run the solver in parallel. We can specify the number of the strips by providing an additional flag to the solver, –nsz. In this example, we will run 16 strips, therefore it would be specified as –nsz 16. The solver can now be run as follows
The simulation results are illustrated in spanwise vorticity contours in Figure 10.15. The wake response of the cable appears as standing wave patter in the earlier stage and then it transitions into traveling wave response, as shown in this figure.
In this example, it will be illustrated how to perform a direct stability analysis using Nektar++. Let us consider a canonical stability problem, the flow in a channel which is confined in the wall-normal direction between two infinite plates (Poiseuille flow) at Reynolds number 7500. This problem is a particular case of the stability solver for the IncNavierStokesSolver.
We consider the linearised Incompressible Navier-Stokes equations:
We are interested to compute the leading eigenvalue of the system using the Arnoldi method.
The geometry under consideration is a 2D channel.
In the GEOMETRY section, the dimensions of the problem are defined. Then, the coordinates
(XSCALE, YSCALE, ZSCALE) of each vertices of each element are specified. As this input file
defines a two-dimensional problem: ZSCALE = 0.
Edges can now be defined by two vertices.
In the ELEMENT section, the tag T and Q define respectively triangular and quadrilateral
element. Triangular elements are defined by a sequence of three edges and quadrilateral
elements by a sequence of four edges.
Finally, collections of elements are listed in the COMPOSITE section and the DOMAIN section
specifies that the mesh is composed by all the triangular and quadrilateral elements. The other
composites will be used to enforce boundary conditions.
This section defines the polynomial expansions used on each composites. For this example we will use a 10th order polynomial, i.e. P = 11.
In this example the EvolutionOperator must be Direct to consider the linearised
Navier-Stokes equations and the Driver was set up to ModifiedArnoldi for the solution of
the eigenproblem.
All the stability parameters are specified in this section.
We need to set up the base flow that can be specified as a function BaseFlow. In case the base
flow is not analytical, it can be generated by means of the Nonlinear evolution operator
using the same mesh and polynomial expansion. The initial guess is specified in the
InitialConditions functions and can be both analytical or a file. In this example it is read
from a file.
IncNavierStokesSolver ChanStability.xml
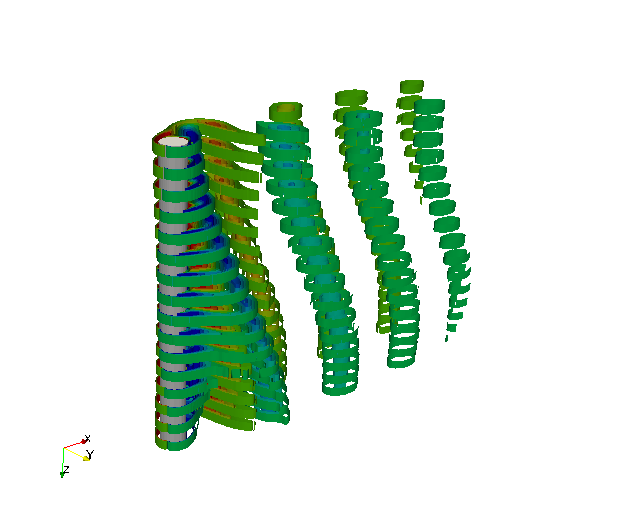
The stability simulation takes about 250 iterations to converge and the dominant eigenvalues (together with the respective eigenvectors) will be printed. In this case it was found λ1,2 = 1.000224 ×e±0.24984i. Therefore, since the magnitude of the eigenvalue is larger than 1, the flow is absolutely unstable. It is possible to visualise the eigenvectors using the post-processing utilities. The figure shows the profile of the two eigenmode component, which shows the typical Tollmien - Schlichting waves that arise in viscous boundary layers.
In this example, it will be illustrated how to perform an adjoint stability analysis using Nektar++. Let us consider a canonical stability problem, the flow in a channel which is confined in the wall-normal direction between two infinite plates (Poiseuille flow) at Reynolds number 7500
We consider the equations:
We are interested in computing the leading eigenvalue of the system using the Arnoldi method.
The geometry and mesh are the same ones used for the direct stability analysis in the previous example.
This sections defines the problem solved. In this example the EvolutionOperator must be
Adjoint to consider the adjoint Navier-Stokes equations and the Driver was set up to
ModifiedArnoldi for the solution of the eigenproblem.
We need to set up the base flow that can be specified as a function BaseFlow. In case the base
flow is not analytical, it can be generated by means of the Nonlinear evolution operator using
the same mesh and polynomial expansion.
The initial guess is specified in the InitialConditions functions and can be both analytical
or a file. In this example it is read from a file.
IncNavierStokesSolver ChanStability_adj.xml
The equations will then be evolved backwards in time (consistently with the negative sign in front of the time derivative) and the leading eigenvalues will be computed after about 300 iterations. It is interesting to note that their value is the same one computed for the direct problem, but the eigenmodes present a different shape.
In this section it will be described how to perform a transient growth stability analysis using Nektar++. Let us consider a flow past a backward-facing step (figure 10.20). This is an important case because it allows us to understand the effects of separation caused by abrupt changes in the geometry and it is a common geometry in several studies of flow control and turbulence of separated flow.
Transient growth analysis allows us to study the presence of convective instabilities that can arise in stable flows. Despite the fact that these instabilities will decay for a long time (due to the stability of the flow), they can produce significant increases in the energy of perturbations. The phenomenon of transient growth is associated with the non-normality of the linearised Navier-Stokes equations and it consists in computing the perturbation that leads to the highest energy growth for a fixed time horizon.
In the GEOMETRY section, the dimensions of the problem are defined. Then, the coordinates
(XSCALE, YSCALE, ZSCALE) of each vertices are specified. As this input file defines a
two-dimensional problem: ZSCALE = 0.
Edges can now be defined by two vertices.
In the ELEMENT section, the tag T and Q define respectively triangular and quadrilateral
element. Triangular elements are defined by a sequence of three edges and quadrilateral
elements by a sequence of four edges.
Finally, collections of elements are listed in the COMPOSITE section and the DOMAIN section
specifies that the mesh is composed by all the triangular and quadrilateral elements. The other
composites will be used to enforce boundary conditions.
For this example we will use a 6th order polynomial, i.e. P = 7:
This sections defines the problem solved. In this example the EvolutionOperator must be
TransientGrowth and the Driver was set up to Arpack for the solution of the
eigenproblem.
We need to set up the base flow that can be specified as a function BaseFlow. In case the base
flow is not analytical, it can be generated by means of the Nonlinear evolution operator using
the same mesh and polynomial expansion.
The initial guess is specified in the InitialConditions functions and in this case is read from
a file.
IncNavierStokesSolver bfs_tg-AR.xml
The solution will be evolved forward in time using the operator A, then backward in time through the adjoint operator A∗. The leading eigenvalue is λ = 3.236204). This corresponds to the largest possible transient growth at the time horizon τ = 1. The leading eigenmode is shown below. This is the optimal initial condition which will lead to the greatest growth when evolved under the linearised Navier-Stokes equations.
It is possible to visualise the transient growth plotting the energy evolution over time if the system is initially perturbed with the leading eigenvector. This analysis was performed for a time horizon τ = 60. It can be seen that the energy grows in time reaching its maximum value at x = 24 and then decays, almost disappearing after 100 temporal units.
In this example it will be described how to run a BiGlobal stability analysis for a time-periodic base flow using Nektar++. Let us consider a flow past a circular cylinder at Re = 220 has a 2D time-periodic wake that is unstable to a 3D synchronous "mode A" instability.
The numerical solution of the fully three- dimensional linear eigenvalue problem is often computationally demanding and may not have significant advantages over performing a direct numerical simulation. Therefore, some simplifications are required; the most radical consist in considering that the base flow depends only on one spatial coordinate, assuming that the other two spatial coordinates are homogenous. While this method offers a good prediction for the instability of boundary layers, it is not able to predict the instability of Hagen-Poiseuille flow in a pipe at all Reynolds numbers. Between a flow that depends upon one and three-spatial directions, it is possible to consider a steady or time-periodic base flow depending upon two spatial directions and impose three-dimensional disturbances that are periodic in the the third homogeneous spatial direction. This approach is known as BiGlobal stability analysis and it represents the extension of the classic linear stability theory; let us consider a base flow U that is function of only two spatial coordinates: mathbfU(x,y,t). The perturbation velocity can u′ can be expressed in a similar form, but with the dependence on the third homogeneous direction incorporated through the Fourier mode: u′ = û′(x,y,t)eiβz, where β = 2π∕L)and L is the length in the homogeneous direction.
In this example we use a mesh of 500 quadrilateral elements with a 6th order polynomial
expansion. The base flow has been computed using the Nonlinear evolution operator with
appropriate boundary conditions. From its profile, it was possible to determine the periodicity
of the flow sampling the velocity profile over time. In order to reconstruct the temporal
behaviour of the flow, 32 time slices were considered over one period. Using these data it is
possible to set up the stability simulation for a specified β, for example β = 1.7. Let us note
that while the base flow is 2D, the stability simulation that we are performing is
3D.
In this example we will use a 6th order polynomial expansion, i.e. P = 7.
IncNavierStokesSolver session.xml
The stability simulation takes about 20 cycles to converge and the leading eigenvalue is λ = 1.2670 with a growth rate σ = 4.7694e − 02. The figure below shows the profile of the magnitude of the eigenmode at z = 2.
