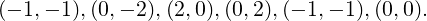
The first example is the classic L-shaped domain, in which an exact solution is known, which makes it an ideal test case [23]. The domain is the polygon formed from the vertices
The exact solution for the displacements is known in polar co-ordinates (r,θ) as
| ur(r,θ) | = 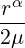 ![[C1(C2 - α - 1)cos((α - 1)θ)- (α + 1)cos((α + 1)θ)]](user-guide162x.png) | ||
| uθ(r,θ) | = 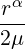 ![[(α + 1)sin((α+ 1)θ) + C1(C2 + α - 1)sin ((α - 1)θ)]](user-guide164x.png) |
where α ≈ 0.544483737… is the solution of the equation α sin(2ω) + sin(2ωα) = 0,
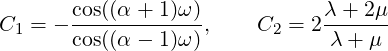
with λ and μ being the Lamé constants and ω = 3π∕4. Boundary conditions are set to be the exact solution and f = 0. The solution has a singularity at the origin, and so in order to test convergence h-refinement is required.
A simple example of how the linear elastic solver can be set up can be found in the
Tests/L-shaped.xml session file in the linear elastic solver directory. A more refined domain
with the obtained u solution is shown in figure 12.1. The solver can be run using the
command:
The obtained solution L-domain.fld can be applied to the mesh to obtain a deformed XML
file using the deform module in FieldConvert:
In this example we use the iterative elastic system to apply a large deformation to a triangular
boundary layer mesh of a square mesh Ω = [0,1]2. At the bottom edge, we apply a Dirichlet
condition g =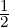 
sin(πx) that is enforced by splitting it into N substeps, so that at each step we
solve the system with the boundary condition gn(x) = g(x)∕N. The process is depicted in
figure 12.2.
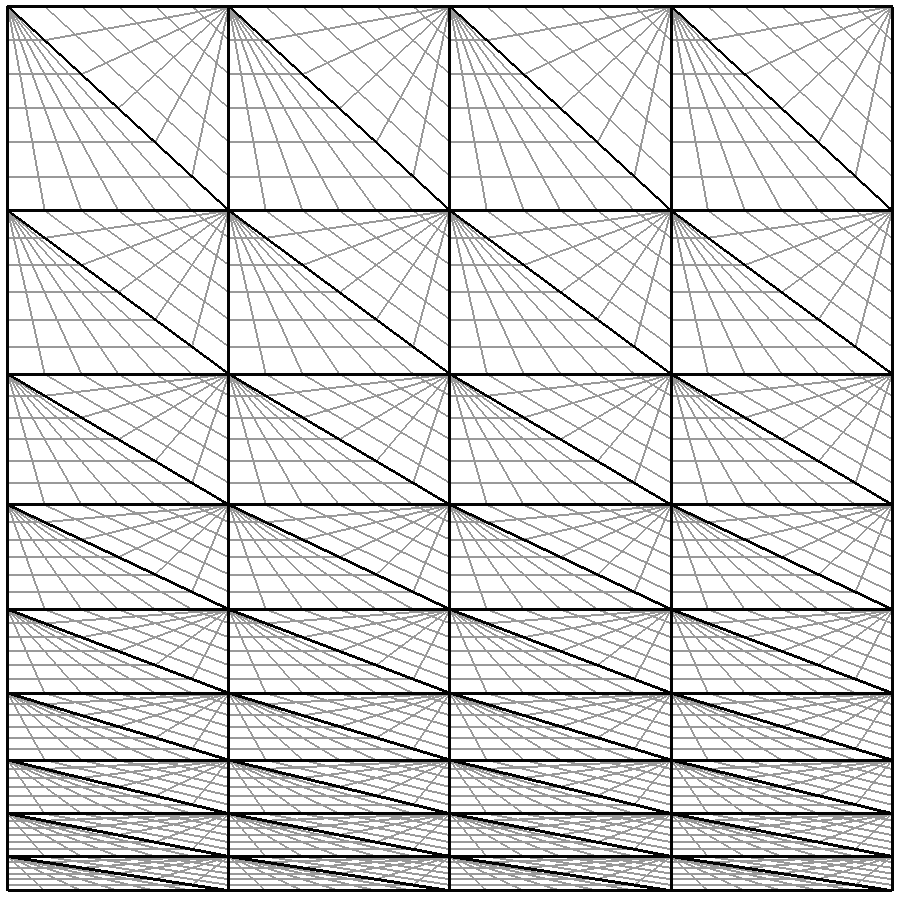
The setup is very straightforward. The geometry can be found inside the file
Examples/bl-mesh.xml and the conditions inside Examples/bl-conditions.xml.
The solver can be set up using the following parameters, with NumSteps denoting
N:
To identify the boundary that we intend to split up into substeps, we must assign the WALL tag
to our boundary regions:
The solver can then be run using the command:
This will produce a series of meshes bl-mesh-%d.xml, where %d is an integer running between
0 and 100. If at any point the mesh becomes invalid, that is, a negative Jacobian is detected,
execution will cease.
