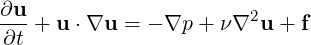 | (11.1a) |
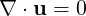 | (11.1b) |
A useful tool implemented in Nektar++ is the incompressible Navier Stokes solver that allows one to solve the governing equation for viscous Newtonians fluids governed by:
where V is the velocity, p is the specific pressure (including density) and ν the kinematic viscosity.
The first approach uses a splitting/projection method where the velocity system and the pressure are typically decoupled. Splitting schemes are typically favoured for their numerical efficiency since the velocity and pressure are handled independently, requiring the solution of three (in two dimensions) elliptic systems of rank N (opposed to a single system of rank 3N solved in the Stokes problem). However, a drawback of this approach is the splitting scheme error which is introduced when decoupling the pressure and the velocity system, although this can be made consistent with the overall temporal accuracy of the scheme by appropriate discretisation of the pressure boundary conditions.
In the original approach a stiffly-stable time integration was proposed in the work of Karniadakis, Israeli and Orszag [20]. This was then later fully analysed in the work of Guermond and Shen [17].
Briefly, high order splitting scheme was originally proposed in three steps involving explicit advection of the non-linear terms, followed by the solution of the pressure Poisson system and finally solving a Helmholtz problem to enforce the viscous terms and velocity boundary conditions. In the following however we briefly formulate this scheme as a two steps using a formulation outline by Guermond and Shen.
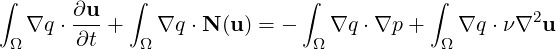 | (11.2) |
where N(u) = u ⋅∇u. We recall that the term ∫ Ω∇q ⋅∇p is the weak approximation to the Laplacian operator for pressure. To decouple this term from the velocity system a few steps are necessary. Using the identity
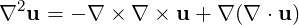
we can enforce the divergence to be zero by setting the last term to zero. If we now integrate the 1st, 2nd and last term in equation (11.2) by parts we can obtain the weak pressure equation
| ∫ Ω∇q ⋅∇pn+1 | = ∫
Ωq ∇⋅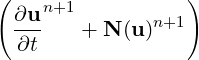 | ||
-∫
∂Ωq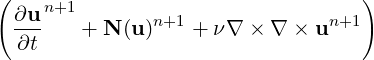 ⋅n ⋅n | (11.3) |
where ∂Ω is the boundary of the domain and we have used the factor that ∇⋅ (∇×∇×u) = 0. To get the final form of the weak pressure Poisson equation we can use a backward approximation of the time derivative to obtain
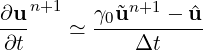 | (11.4) |
where 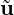 n+1 is an intermediate velocity upon which to decouple the system we impose
that ∇⋅
n+1 is an intermediate velocity upon which to decouple the system we impose
that ∇⋅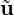 n+1 = 0 and
n+1 = 0 and
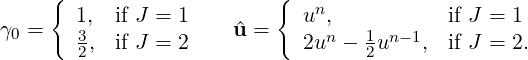
Finally we introduce a consistent extrapolation for the non-linear terms and the curl of vorticity terms of the form:
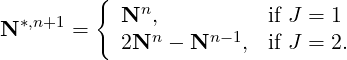
A similar extrapolation can be used on the curl-curl term to end up with the final weak pressure approximation
| ∫ Ω∇q ⋅∇pn+1 | = ∫
Ωq ∇⋅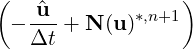 | ||
-∫
∂Ωq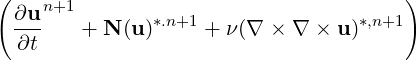 ⋅n ⋅n | (11.5) |
We note this can be recast into an equivalent strong form of the pressure Poisson equation of the form
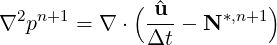 | (11.6) |
with consistent Neumann boundary conditions prescribed as
![∂p-n+1 [∂u-n+1 *,n+1 *,n+1]
∂n = - ∂t + ν(∇ × ∇ × u ) + N ⋅n](user-guide102x.png) | (11.7) |
In this step now approximate the time derivative using
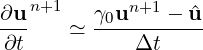 | (11.8) |
which leads us to the Helmholtz problem
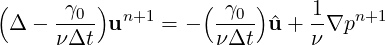 | (11.9) |
This scheme is activated in the SolverInfo section with the SolverType specification:
As presented in the previous section in the work of Guermond and Shen [17] and subsequent work they formulate the pressure in a weak rather than strong form to obtain the pressure Poisson system. Therefore if we take the inner product of equation (11.1a) with respect to the gradient of the test space, ∇q, we obtain equation (11.2)
We again make the approximation
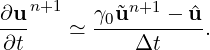 | (11.10) |
However this time we only integrate by parts the last term and do not integrate the non-linear
term by parts. However we still need to enforce the condition that ∇⋅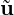 n+1 = 0 and so we also
integrate just this part of the time derivate by parts to arrive at a weak pressure system of the
form:
n+1 = 0 and so we also
integrate just this part of the time derivate by parts to arrive at a weak pressure system of the
form:
| ∫ Ω∇q ⋅∇pn+1+ | 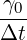 ∫
∂Ω0q ∫
∂Ω0q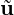 n+1 ⋅n = ∫
Ω∇q ⋅ ( n+1 ⋅n = ∫
Ω∇q ⋅ (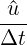 -N⋆,n+1) -N⋆,n+1) | ||
-∫
∂Ω
d⋃
∂Ω0q ν(∇×∇×u)*,n+1 ⋅n + 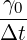 ∫
∂Ωdqwn+1 ⋅n ∫
∂Ωdqwn+1 ⋅n | (11.11) |
where ∂Ωd is the Dirichlet boundary conditions for the velocity and ∂Ω0 is the outflow boundary.
This scheme is activated in the SolverInfo section with the SolverType specification:
In order to specify the pressure boundary conditions given by equation (11.7) or for the
equivalent conditions in the VCSWeakPressure scheme the USERDEFINEDTYPE condition “H”
can be used. Therefore a zero velocity wall boundary condition on boundary region 0 in
two-dimensions can be specified as
The most straightforward outflow condition is to specify fully developed conditions of ∇un+1 ⋅n = 0 and p = 0 which can be specified as
However when energetic vortices pass through an outflow region one can experience instabilities as identified by the work of Dong, Karnidakis and Chryssostomidis [11]. In this paper they suggest to impose a pressure Dirichlet outflow condition of the form
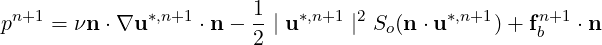 | (11.12) |
with a step function defined by So(n ⋅u) = 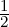 (1 - tanh
(1 - tanh 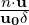 ), where u0 is the characteristic
velocity scale and δ is a non-dimensional positive constant chosen to be sufficiently small. fb is
the forcing term in this case the analytical conditions can be given but if these are not known
explicitly, it is set to zero, i.e. fb = 0. (see the test KovaFlow_m8_short_HOBC.xml
for a non-zero example). Note that in the paper [11] they define this term as the
negative of what is shown here so that it could be use used to impose a default
pressure values. This does however mean that the forcing term is imposed through the
velocity components u,v by specifying the entry
), where u0 is the characteristic
velocity scale and δ is a non-dimensional positive constant chosen to be sufficiently small. fb is
the forcing term in this case the analytical conditions can be given but if these are not known
explicitly, it is set to zero, i.e. fb = 0. (see the test KovaFlow_m8_short_HOBC.xml
for a non-zero example). Note that in the paper [11] they define this term as the
negative of what is shown here so that it could be use used to impose a default
pressure values. This does however mean that the forcing term is imposed through the
velocity components u,v by specifying the entry VALUE (An example can be found in
ChanFlow_m3_VCSWeakPress_ConOBC.xml). For the velocity component one can
specify
![[ ]
∇un+1 ⋅ n = 1-pn+1n + 1-| u *,n+1 |2 S (n ⋅u*,n+1) - ν(∇ ⋅u*,n+1)n- fn+1
ν 2 o b](user-guide114x.png) | (11.13) |
This condition can be enforced using the USERDEFINEDTYPE “HOutflow”, i.e.
Note that in the moving body work of Bao et al. [4] some care must be made to identify when the flow over the boundary is incoming or outgoing and so a modification of the term
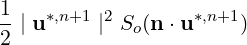
is replaced with
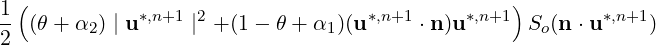
where the default values are given by θ = 1,α1 = 0,α2 = 0 and these values can be set through
the parameters OutflowBC_theta, OutflowBC_alpha1 and OutflowBC_alpha2.
Dong has also suggested convective like outflow conditions in [10] which can be enforced through a Robin type specification of the form
![n+1 [
∂u---- + γ0D0-un+1 = 1- fn+1 + E (n,u*,n+1)+ pn+1n - ν(∇ ⋅u *,n+1)n] + D0-^u
∂n Δt ν Δt](user-guide117x.png) | (11.14) |
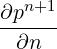 + + 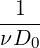 pn+1 pn+1 | = -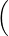 -ν(∇×∇×u)*,n+1 + N*,n+1 -ν(∇×∇×u)*,n+1 + N*,n+1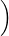 ⋅n ⋅n | ||
-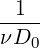 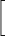 fn+1 + E(n,u*,n+1 + pn+1n - ν(∇⋅u*,n+1)n fn+1 + E(n,u*,n+1 + pn+1n - ν(∇⋅u*,n+1)n![]](user-guide124x.png) | (11.15) |
It is possible to use different time steps in the velocity correction scheme using a substepping (also known as subcycling) [38] or auxiliary semi-Lagrangian approach [46]. Originally the scheme was proposed by Maday, Patera and Ronquist who referred to as an operator-integration-factor splitting method [27]

A schematic of the approach can be understood from figure 11.1.1.5 where we observe that
smaller time steps can be used for the explicit advection steps whilst a larger overall time step
is adopted for the more expensive implicit solve for the diffusion operator. More details of the
implementation can be found in [46] and [38]. In the following sections we outline the
parameters that can be used to set up this scheme. Since the explicit part is advanced using a
DG scheme it is necessary to use a Mixed_CG_Discontinuous expansion with this
option.
$NEKHOME/Solver/IncNavierStokesSolver/Tests/ directory:
KovaFlow_SubStep_2order.xml, Hex_Kovasnay_SubStep.xml and Tet_Kovasnay_SubStep.xml.
For well resolved simulations it appears that often using the same polynomial space for the pressure and velocity does give suitable answer but this does not satisfy the so-called LBB or inf-sup condition. Therefore, it is potentially better to specify an equivalent of the Taylor Hood approximation and use one higher polynomial order for velocity than the pressure with a continuous expansion. To specify this type of expansion you can use an expansion section of the form:
In the above example the “u,v” fields are specified to have a polynomial order of 7 using a
modified expansion. Implicitly this form of the expansion definition uses a quadrature order of
9. The above definition then also uses a modified expansion for pressure but of polynomial
order 6. Since currently for this solver to run we need to use a consistent quadrature order for
both the velocity and pressure fields we specify the MODIFIEDQUADPLUS1 to tell the solver to
use an additional quadrature point and therefore also use 9 quadrature points in each 1D
direction for the pressure.
In other cases it is sometimes useful to run with an even higher quadrature order, for example to handle highly deformed elements where the Jacobian is represented by a polynomial expansion. This can be done by using a more detailed definition of the expansion of the form:
In this example we have specified an 8th order expansion for “u,v” and a 7th order expansion for “p”. The BasisType is given as “Modified_A, Modified_B” which is for a triangular expansion (note that for a quadrilateral expansion it would have been “Modified_A,Modified_A”) and so the number of quadrature points in this case is 9 in the first direction which uses Gauss-Lobatto-Legendre points but only 8 in the second direction since this uses a Gauss-Radau formula with α = 1,β = 0 weights (see [21] for details on why).
The second approach consists of directly solving the matrix problem arising from the discretization of the Stokes problem. The direct solution of the Stokes system introduces the problem of appropriate spaces for the velocity and the pressure systems to satisfy the inf-sup condition and it requires the solution of the full velocity-pressure system. However, if a discontinuous pressure space is used then all but the constant mode of the pressure system can be decoupled from the velocity. When implementing this approach with a spectral/hp element discretization, the remaining velocity system may then also be statically condensed to decouple the so called interior elemental degrees of freedom, reducing the Stokes problem to a smaller system expressed on the elemental boundaries. The direct solution of the Stokes problem provides a very natural setting for the solution of the pressure system which is not easily dealt with in a splitting scheme. Further, the solution of the full coupled velocity system allows the introduction of a spatially varying viscosity, which arise for non-Newtonian flows, with only minor modifications.
DirectStaticCond) which prevents its use in
parallel.
We consider the weak form of the Stokes problem for the velocity field u = [u,v]T and the pressure field p:
where the components of A,B and C are ∇ϕb,ν∇ub, ∇ϕb,ν∇ui and ∇ϕi,ν∇ui and the components Db and Di are q,∇ub and q,∇ui. The indices b and i refer to the degrees of freedom on the elemental boundary and interior respectively. In constructing the system we have lumped the contributions form each component of the velocity field into matrices A,B and C. However, we note that for a Newtonian fluid the contribution from each field is decoupled. Since the interior degrees of freedom of the velocity field do not overlap, the matrix C is block diagonal and to take advantage of this structure we can statically condense out the C matrix to obtain the system:
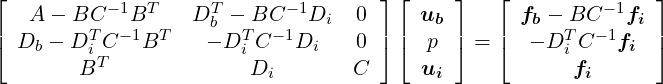 | (11.17) |
To extend the above Stokes solver to an unsteady Navier-Stokes solver we first introduce the unsteady term, ∂u∕∂t, into the Stokes problem. This has the principal effect of modifying the weak Laplacian operator ∇ϕ,ν∇u] into a weak Helmholtz operator ∇ϕ,ν∇u) -λ(ϕ,u where λ depends on the time integration scheme. The second modification requires the explicit discretisation of the non-linear terms in a similar manner to the splitting scheme and this term is then introduced as the forcing term f. For more details see [1, 39].
Hydrodynamic stability is an important part of fluid-mechanics that has a relevant role in understanding how an unstable flow can evolve into a turbulent state of motion with chaotic three-dimensional vorticity fields and a broad spectrum of small temporal and spatial scales. The essential problems of hydrodynamic stability were recognised and formulated in 19th century, notably by Helmholtz, Kelvin, Rayleigh and Reynolds.
Conventional linear stability assumes a normal representation of the perturbation fields that can be represented as independent wave packets, meaning that the system is self-adjoint. The main aim of the global stability analysis is to evaluate the amplitude of the eigenmodes as time grows and tends to infinity. However, in most industrial applications, it is also interesting to study the behaviour at intermediate states that might affects significantly the functionality and performance of a device. The study of the transient evolution of the perturbations is seen to be strictly related to the non-normality of the linearised Navier-Stokes equations, therefore the normality assumption of the system is no longer assumed. The eigenmodes of a non-normal system do not evolve independently and their interaction is responsible for a non-negligible transient growth of the energy. Conventional stability analysis generally does not capture this behaviour, therefore other techniques should be used.
A popular approach to study the hydrodynamic stability of flows consists in performing a direct numerical simulation of the linearised Navier-Stokes equations using iterative methods for computing the solution of the associated eigenproblem. However, since linearly stable flows could show a transient increment of energy, it is necessary to extend this analysis considering the combined effect of the direct and adjoint evolution operators. This phenomenon has noteworthy importance in several engineering applications and it is known as transient growth.
In Nektar++ it is then possible to use the following tools to perform stability analysis:
The equations that describe the evolution of an infinitesimal disturbance in the flow can be derived decomposing the solution into a basic state (U,p) and a perturbed state U + εu′ with ε « 1 that both satisfy the Navier-Stokes equations. Substituting into the Navier-Stokes equations and considering that the quadratic terms u′⋅∇u′ can be neglected, we obtain the linearised Navier-Stokes equations:
The linearised Navier-Stokes equations are identical in form to the non-linear equation, except for the non-linear advection term. Therefore the numerical techniques used for solving Navier-Stokes equations can still be applied as long as the non-linear term is substituted with the linearised one. It is possible to define the linear operator that evolved the perturbation forward in time:
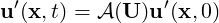 | (11.19) |
Let us assume that the base flow U is steady, then the perturbations are autonomous and we can assume that:
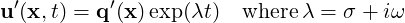 | (11.20) |
Then we obtain the associated eigenproblem:
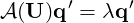 | (11.21) |
The dominant eigenvalue determines the behaviour of the flow. If the real part is positive then there exist exponentially growing solutions. Conversely, if all the eigenvalues have negative real part then the flow is linearly stable. If the real part of the eigenvalue is zero, it is a bifurcation point.
The adjoint of a linear operator is one of the most important concepts in functional analysis and it plays an important role in understanding transition to turbulence. Let us write the linearised Navier-Stokes equation in a compact form:
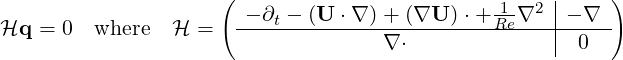 | (11.22) |
The adjoint operator H* is defined as:
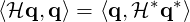 | (11.23) |
Integrating by parts and employing the divergence theorem, it is possible to express the adjoint equations:
The adjoint fields are in fact related to the concept of receptivity. The value of the adjoint velocity at a point in the flow indicates the response that arises from an unsteady momentum source at that point. The adjoint pressure and the adjoint stream function play instead the same role for mass and vorticity sources respectively. Therefore, the adjoint modes can be seen as a powerful tool to understand where to act in order to ease/inhibit the transition.
Transient growth is a phenomenon that occurs when a flow that is linearly stable, but whose perturbations exhibit a non-negligible transient response due to regions of localised convective instabilities. This situation is common in many engineering applications, for example in open flows where the geometry is complex, producing a steep variation of the base flow. Therefore, the main question to answer is if it exists a bounded solution that exhibit large growth before inevitably decaying. Let us introduce a norm to quantify the size of a perturbation. It is physically meaningful to use the total kinetic energy of a perturbation on the domain Ω. This is convenient because it is directly associated with the standard-L2 inner product:
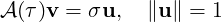 | (11.25) |
where σ = 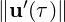 . This is no other than the singular value decomposition of A(τ). The
phenomenology of the transient growth can be explained considering the non-normality of the
linearised Navier-Stokes evolution operator. This can be simply understood using the simple
geometric example showed in figure 11.1.3.3. Let us assume a unit-length vector f
represented in a non-orthogonal basis .This vector is defined as the difference of the
nearly collinear vectors Φ1 and Φ2. With the time progression, the component of
these two vectors decrease respectively by 20% and 50%. The vector f increases
substantially in length before decaying to zero. Thus, the superposition of decaying
non-orthogonal eigenmode can produce in short term a growth in the norm of the
perturbations.
. This is no other than the singular value decomposition of A(τ). The
phenomenology of the transient growth can be explained considering the non-normality of the
linearised Navier-Stokes evolution operator. This can be simply understood using the simple
geometric example showed in figure 11.1.3.3. Let us assume a unit-length vector f
represented in a non-orthogonal basis .This vector is defined as the difference of the
nearly collinear vectors Φ1 and Φ2. With the time progression, the component of
these two vectors decrease respectively by 20% and 50%. The vector f increases
substantially in length before decaying to zero. Thus, the superposition of decaying
non-orthogonal eigenmode can produce in short term a growth in the norm of the
perturbations.
To compute linear stability analysis, the choice of the base flow, around which the system will be linearised, is crucial. If one wants to use the steady-state solution of the Navier-Stokes equations as base flow, a steady-state solver is implemented in Nektar++. The method used is the encapsulated formulation of the Selective Frequency Damping method [19]. Unstable steady base flows can be obtained with this method. The SFD method is based on the filtering and control of unstable temporal frequencies within the flow. The time continuous formulation of the SFD method is
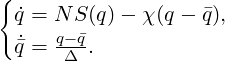 | (11.26) |
where q represents the problem unknown(s), the dot represents the time derivative, NS represents the Navier-Stokes equations, χ ∈ ℝ+ is the control coefficient, is a filtered version of q, and Δ ∈ ℝ+* is the filter width of a first-order low-pass time filter. The steady-state solution is reached when q = .
The convergence of the method towards a steady-state solution depends on the choice of the parameters χ and Δ. They have to be carefully chosen: if they are too small, the instabilities within the flow can not be damped; but if they are too large, the method may converge extremely slowly. If the dominant eigenvalue of the flow studied is known (and given as input), the algorithm implemented can automatically select parameters that ensure a fast convergence of the SFD method. Most of the time, the dominant eigenvalue is not know, that is why an adaptive algorithm that adapts χ and Δ all along the solver execution is also implemented.
Note that this method can not be applied for flows with a pure exponential growth of the instabilities (e.g. jet flow within a pipe). In other words, if the frequency of the dominant eigenvalue is zero, then the SFD method is not a suitable tool to obtain a steady-state solution.