5.6 FieldConvert modules -m

FieldConvert allows the user to manipulate the Nektar++ output binary files (.chk and .fld) by using the flag -m (which stands for module). Specifically, FieldConvert has these additional functionalities

1. C0Projection: Computes the C0 projection of a given output file;
2. CFL: Computes the CFL number over the solution domain for Incompressible flow
3. QCriterion: Computes the Q-Criterion for a given output file;
4. L2Criterion: Computes the Lambda 2 Criterion for a given output file;
5. addcompositeid: Adds the composite ID of an element as an additional field;
6. fieldfromstring: Modifies or adds a new field from an expression involving the existing fields;
7. addFld: Sum two .fld files;
8. combineAvg: Combine two Nektar++ binary output (.chk or .fld) field file containing averages of fields (and possibly also Reynolds stresses) into single file;
9. concatenate: Concatenate a Nektar++ binary output (.chk or .fld) field file into single file (deprecated);
10. dof: Count the total number of DOF;
11. equispacedoutput: Write data as equi-spaced output using simplices to represent the data for connecting points;
12. extract: Extract a boundary field;
13. gradient: Computes gradient of fields;
14. halfmodetofourier: Convert HalfMode expansion to SingleMode for further processing;
15. homplane: Extract a plane from 3DH1D expansions;
16. homstretch: Stretch a 3DH1D expansion by an integer factor;
17. innerproduct: take the inner product between one or a series of fields with another field (or series of fields).
18. interpfield: Interpolates one field to another, requires fromxml, fromfld to be defined;
19. interppointdatatofld: Interpolates given discrete data using a finite difference approximation to a fld file given an xml file;
20. interppoints: Interpolates a field to a set of points. Requires fromfld, fromxml to be defined, and a topts, line, plane or box of target points;
21. interpptstopts: Interpolates a set of points to another. Requires a topts, line, plane or box of target points;
22. isocontour: Extract an isocontour of “fieldid” variable and at value “fieldvalue”. Optionally “fieldstr” can be specified for a string definition or “smooth” for smoothing;
23. jacobianenergy: Shows high frequency energy of Jacobian;
24. qualitymetric: Evaluate a quality metric of the underlying mesh to show mesh quality;
25. mean: Evaluate the mean of variables on the domain;
26. meanmode: Extract mean mode (plane zero) of 3DH1D expansions;
27. pointdatatofld: Given discrete data at quadrature points project them onto an expansion basis and output fld file;
28. printfldnorms: Print L2 and LInf norms to stdout;
29. removefield: Removes one or more fields from .fld files;
30. scalargrad: Computes scalar gradient field;
31. scaleinputfld: Rescale input field by a constant factor;
32. shear: Computes time-averaged shear stress metrics: TAWSS, OSI, transWSS, TAAFI, TACFI, WSSG;
33. streamfunction: Calculates stream function of a 2D incompressible flow.
34. surfdistance: Computes height of a prismatic boundary layer mesh and projects onto the surface (for e.g. y⁺ calculation).
35. vorticity: Computes the vorticity field.
36. wss: Computes wall shear stress field.
37. phifile: Computes the Φ function representing a body defined in an .stl file. Useful for the Smoothed Profile Method solver.
38. wallNormalData: Interpolate values for a set of points in the wall-normal direction (for e.g. extract boundary layer profiles).

The module list above can be seen by running the command

In the following we will detail the usage of each module.

5.6.1 Smooth the data: C0Projection module

To smooth the data of a given .fld file one can use the C0Projection module of FieldConvert

where the file test-C0Proj.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

The option localtoglobalmap will do a global gather of the coefficients and then scatter them back to the local elements. This will replace the coefficients shared between two elements with the coefficients of one of the elements (most likely the one with the highest id). Although not a formal projection it does not require any matrix inverse and so is very cheap to perform.

The option usexmlbcs will enforce the boundary conditions specified in the input xml file.

The option helmsmoothing=L will perform a Helmholtz smoothing projection of the form

which can be interpreted in a Fourier sense as smoothing the original coefficients using a low pass filter of the form

and so L is the length scale below which the coefficients values are halved or more. Since this form of the Helmholtz operator is not possitive definite, currently a direct solver is necessary and so this smoother is mainly of use in two-dimensions.

5.6.2 Calculate CFL number: CFL module

This module calculates the CFL number over the domain. It currently only supports the solution results from the Incompressible flow simulaitons, i.e. the outputs of IncNavierStokesSolver. To Estimate the CFL number, the user can run

where the file test-cfl.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.3 Calculate Q-Criterion: QCriterion module

To perform the Q-criterion calculation and obtain an output data containing the Q-criterion solution, the user can run

where the file test-QCrit.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.4 Calculate λ₂: L2Criterion module

To perform the λ₂ vortex detection calculation and obtain an output data containing the values of the λ₂ eigenvalue, the user can run

where the file test-L2Crit.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.5 Add composite ID: addcompositeid module

When dealing with a geometry that has many surfaces, we need to identify the composites to assign boundary conditions. To assist in this, FieldConvert has a addcompositeid module, which adds the composite ID of every element as a new field. To use this we simply run

In this case, we have produced a Tecplot file which contains the mesh and a variable that contains the composite ID. To assist in boundary identification, the input file mesh.xml should be a surface XML file that can be obtained through the NekMesh extract module (see section 4.5.3).

5.6.6 Add new field: fieldfromstring module

To modify or create a new field using an expression involving the existing fields, one can use the fieldfromstring module of FieldConvert

In this case fieldstr is a required parameter describing a function of the coordinates and the existing variables, and fieldname is an optional parameter defining the name of the new or modified field (the default is newfield). file3.fld is the output containing both the original and the new fields, and can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.7 Sum two .fld files: addFld module

To sum two .fld files one can use the addFld module of FieldConvert

In this case we use it in conjunction with the command scale which multiply the values of a given .fld file by a constant value. file1.fld is the file multiplied by value, file1.xml is the associated session file, file2.fld is the .fld file which is summed to file1.fld and finally file3.fld is the output which contain the sum of the two .fld files. file3.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.8 Combine two .fld files containing time averages: combineAvg module

To combine two .fld files obtained through the AverageFields or ReynoldsStresses filters, use the combineAvg module of FieldConvert

file3.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.9 Concatenate two files: concatenate module

To concatenate file1.fld and file2.fld into file-conc.fld one can run the following command

where the file file-conc.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt. The concatenate module previously used for this purpose is not required anymore, and will be removed in a future release.

5.6.10 Count the number of DOF: dof module

To count the number of DOF in a solution file, one can run the following command

5.6.11 Equi-spaced output of data: equispacedoutput module

This module interpolates the output data to a truly equispaced set of points (not equispaced along the collapsed coordinate system). Therefore a tetrahedron is represented by a tetrahedral number of poinst. This produces much smaller output files. The points are then connected together by simplices (triangles and tetrahedrons).

or

5.6.12 Extract a boundary region: extract module

The boundary region of a domain can be extracted from the output data using the following command line

The option bnd specifies which boundary region to extract. Note this is different to NekMesh where the parameter surf is specified and corresponds to composites rather boundaries. If bnd is not provided, all boundaries are extracted to different fields. The output will be placed in test-boundary_b2.fld. If more than one boundary region is specified the extension _b0.fld, _b1.fld etc will be outputted. To process this file you will need an xml file of the same region. This can be generated using the command:

The surface to be extracted in this command is the composite number and so needs to correspond to the boundary region of interest. Finally to process the surface file one can use

This will obviously generate a Tecplot output if a .dat file is specified as last argument. A .vtu extension will produce a Paraview or VisIt output.

5.6.13 Compute the gradient of a field: gradient module

To compute the spatial gradients of all fields one can run the following command

where the file file-grad.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.14 Convert HalfMode expansion to SingleMode for further processing: halfmodetofourier module

To obtain full Fourier expansion form a HalfMode result, use the comand:

In linear stability analysis with halfmode expansion, the variable w, whose variable number is 2, is a imaginary mode but it is output as a real mode in the eigenvector field file. By setting option realmodetoimag=2, w can be transformed to a imaginary mode correctly.

5.6.15 Extract a plane from 3DH1D expansion: homplane module

To obtain a 2D expansion containing one of the planes of a 3DH1D field file, use the command:

If the option wavespace is used, the Fourier coefficients corresponding to planeid are obtained. The command in this case is:

The output file file-plane.fld can be processed in a similar way as described in section 5.2 to visualise it either in Tecplot or in Paraview.

5.6.16 Stretch a 3DH1D expansion: homstretch module

To stretch a 3DH1D expansion in the z-direction, use the command:

The number of modes in the resulting field can be chosen using the command-line parameter --output-points-hom-z.

The output file file-stretch.fld can be processed in a similar way as described in section 5.2 to visualise it either in Tecplot or in Paraview.

5.6.17 Inner Product of a single or series of fields with respect to a single or series of fields: innerproduct module

You can take the inner product of one field with another field using the following command:

This command will load the file1.fld and file2.fld assuming they both are spatially defined by files.xml and determine the inner product of these fields. The input option fromfld must therefore be specified in this module.

Optional arguments for this module are fields which allow you to specify the fields that you wish to use for the inner product, i.e.

will only take the inner product between the variables 0,1 and 2 in the two fields files. The default is to take the inner product between all fields provided.

Additional options include multifldids and allfromflds which allow for a series of fields to be evaluated in the following manner:

will take the inner product between a file names field1_0.fld, field1_1.fld, field1_2.fld and field1_3.fld with respect to field2.fld.

Analogously including the options allfromflds, i.e.

Will take the inner product of all the from fields, i.e. field1_0.fld,field1_1.fld,field1_2.fld and field1_3.fld with respect to each other. This option essentially ignores file2.fld. Only the unique inner products are evaluated so if four from fields are given only the related trianuglar number 4 × 5∕2 = 10 of inner products are evaluated.

This option can be run in parallel.

5.6.18 Interpolate one field to another: interpfield module

To interpolate one field to another, one can use the following command:

This command will interpolate the field defined by file1.xml and file1.fld to the new mesh defined in file2.xml and output it to file2.fld. The fromxml and fromfld must be specified in this module. In addition there are two optional arguments clamptolowervalue and clamptouppervalue which clamp the interpolation between these two values. Their default values are -10,000,000 and 10,000,000.

If the fromfld is a 3DH1D field and uses HalfMode expansion, you can use realmodetoimag=n1,n2,...,nm to transform the n₁,n₂,...,n_mth variables from real modes to imaginary modes. Variable index starts from 0.

5.6.19 Interpolate scattered point data to a field: interppointdatatofld module

To interpolate discrete point data to a field, use the interppointdatatofld module:

or alternatively for csv data:

This command will interpolate the data from file1.pts (file1.csv) to the mesh and expansions defined in file1.xml and output the field to file1.fld. The file file.pts must be of the form:

where DIM="1" FIELDS="a,b,c specifies that the field is one-dimensional and contains three variables, a, b, and c. Each line defines a point, while the first column contains its x-coordinate, the second one contains the a-values, the third the b-values and so on. In case of n-dimensional data, the n coordinates are specified in the first n columns accordingly. An equivalent csv file is:

In order to interpolate 1D data to a nD field, specify the matching coordinate in the output field using the interpcoord argument:

This will interpolate the 1D scattered point data from 1D-file1.pts to the y-coordinate of the 3D mesh defined in 3D-file1.xml. The resulting field will have constant values along the x and z coordinates. For 1D Interpolation, the module implements a quadratic scheme and automatically falls back to a linear method if only two data points are given. A modified inverse distance method is used for 2D and 3D interpolation. Linear and quadratic interpolation require the data points in the .pts-file to be sorted by their location in ascending order. The Inverse Distance implementation has no such requirement.

5.6.20 Interpolate a field to a series of points: interppoints module

You can interpolate one field to a series of given points using the following command:

This command will interpolate the field defined by file1.xml and file1.fld to the points defined in file2.pts and output it to file2.dat. The fromxml and fromfld must be specified in this module. The format of the file file2.pts is of the same form as for the interppointdatatofld module:

Similar to the interppointdatatofld module, the .pts file can be interchanged with a .csv file (the output can also be written to .csv):

There are three optional arguments clamptolowervalue, clamptouppervalue and defaultvalue the first two clamp the interpolation between these two values and the third defines the default value to be used if the point is outside the domain. Their default values are -10,000,000, 10,000,000 and 0.

In addition, instead of specifying the file file2.pts, a module list of the form

can be specified where npts is the number of equispaced points between (x₀,y₀) to (x₁,y₁). This also works in 3D, by specifying (x₀,y₀,z₀) to (x₁,y₁,z₁).

An extraction of a plane of points can also be specified by

where npts1,npts2 is the number of equispaced points in each direction and (x₀,y₀,z₀), (x₁,y₁,z₁), (x₂,y₂,z₂) and (x₃,y₃,z₃) define the plane of points specified in a clockwise or anticlockwise direction.

In addition, an extraction of a box of points can also be specified by

where npts1,npts2,npts3 is the number of equispaced points in each direction and (x_min,y_min,z_min) and (x_max,y_max,z_max) define the limits of the box of points.

There is also an additional optional argument cp=p0,q which adds to the interpolated fields the value of c_p = (p-p0)∕q and c_p0 = (p-p0 + 0.5u²)∕q where p0 is a reference pressure and q is the free stream dynamics pressure. If the input does not contain a field “p” or a velocity field “u,v,w” then cp and cp0 are not evaluated accordingly.

If the fromfld is a 3DH1D field and uses HalfMode expansion, you can use realmodetoimag=n1,n2,...,nm to transform the n₁,n₂,...,n_mth variables from real modes to imaginary modes. Variable index starts from 0.

5.6.21 Interpolate a set of points to another: interpptstopts module

You can interpolate one set of points to another using the following command:

This command will interpolate the data in file1.pts to a new set of points defined in file2.pts and output it to file2.dat.

Similarly to the interppoints module, the target point distribution can also be specified using the line, plane or box options. The optional arguments clamptolowervalue, clamptouppervalue, defaultvalue and cp are also supported with the same meaning as in interppoints.

One useful application for this module is with 3DH1D expansions, for which currently the interppoints module does not work. In this case, we can use for example

With this usage, the equispacedoutput module will be automatically called to interpolate the field to a set of equispaced points in each element. The result is then interpolated to a plane by the interpptstopts module.

5.6.22 Isocontour extraction: iscontour module

Extract an isocontour from a field file. This option automatically take the field to an equispaced distribution of points connected by linear simplicies of triangles or tetrahedrons. The linear simplices are then inspected to extract the isocontour of interest. To specify the field fieldid can be provided giving the id of the field of interest and fieldvalue provides the value of the isocontour to be extracted.

Alternatively fieldstr="u+v" can be specified to calculate the field u + v and extract its isocontour. You can also specify fieldname="UplusV" to define the name of the isocontour in the .dat file, i.e.

Optionally smooth can be specified to smooth the isocontour with default values smoothnegdiffusion=0.495, smoothnegdiffusion=0.5 and smoothiter=100. This option typically should be used wiht the globalcondense option which removes multiply defined verties from the simplex definition which arise as isocontour are generated element by element. The smooth option preivously automatically called the globalcondense option but this has been depracated since it is now possible to read isocontour files directly and so it is useful to have these as separate options.

In addition to the smooth or globalcondense options you can specify removesmallcontour=100 which will remove separate isocontours of less than 100 triangles.

5.6.23 Show high frequency energy of the Jacobian: jacobianenergy module

The option topmodes can be used to specify the number of top modes to keep.

The output file jacenergy.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.24 Calculate mesh quality: qualitymetric module

The qualitymetric module assesses the quality of the mesh by calculating a per-element quality metric and adding an additional field to any resulting output. This does not require any field input, therefore an example usage looks like

Two quality metrics are implemented that produce scalar fields Q:

• By default a metric outlined in [14] is produced, where all straight sided elements have quality Q = 1 and Q < 1 shows the deformation between the curved element and the straight-sided element. If Q = 0 then the element is invalid. Note that Q varies over the volume of the element but is not guaranteed to be continuous between elements.
• Alternatively, if the scaled option is passed through to the module, then the scaled Jacobian
  

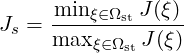
  (i.e. the ratio of the minimum to maximum Jacobian of each element) is calculated. Again Q = 1 denotes an ideal element, but now invalid elements are shown by Q < 0. Any elements with Q near zero are determined to be low quality.

5.6.25 Evaluate the mean of variables on the domain: mean module

To evaluate the mean of variables on the domain one can use the mean module of FieldConvert

This module does not create an output file which is reinforced by the out.stdout option. The integral and mean for each field variable are then printed to the stdout.

5.6.26 Extract mean mode of 3DH1D expansion: meanmode module

To obtain a 2D expansion containing the mean mode (plane zero in Fourier space) of a 3DH1D field file, use the command:

The output file file-mean.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot or in Paraview or VisIt.

5.6.27 Project point data to a field: pointdatatofld module

To project a series of points given at the same quadrature distribution as the .xml file and write out a .fld file use the pointdatatofld module:

This command will read in the points provided in the file.pts and assume these are given at the same quadrature distribution as the mesh and expansions defined in file.xml and output the field to file.fld. If the points do not match an error will be dumped.

The file file.pts which is assumed to be given by an interpolation from another source is of the form:

where DIM="3" FIELDS="p specifies that the field is three-dimensional and contains one variable, p. Each line defines a point, the first, second, and third columns contains the x,y,z-coordinate and subsequent columns contain the field values, in this case the p-value So in the general case of n-dimensional data, the n coordinates are specified in the first n columns accordingly followed by the field data. Alternatively, the file.pts can be interchanged with a csv file.

The default argument is to use the equispaced (but potentially collapsed) coordinates which can be obtained from the command.

In this case the pointdatatofld module should be used without the –noequispaced option. However this can lead to problems when peforming an elemental forward projection/transform since the mass matrix in a deformed element can be singular as the equispaced points do not have a sufficiently accurate quadrature rule that spans the polynomial space. Therefore it is advisable to use the set of points given by

which produces a set of points at the gaussian collapsed coordinates.

Finally the option setnantovalue=0 can also be used which sets any nan values in the interpolation to zero or any specified value in this option.

5.6.28 Print L2 and LInf norms: printfldnorms module

This module does not create an output file which is reinforced by the out.stdout option. The L2 and LInf norms for each field variable are then printed to the stdout.

5.6.29 Removes one or more fields from .fld files: removefield module

This module allows to remove one or more fields from a .fld file:

where the file test-removed.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt. The lighter resulting file speeds up the postprocessing of large files when not all fields are required.

5.6.30 Computes the scalar gradient: scalargrad module

The scalar gradient of a field is computed by running:

The option bnd specifies which boundary region to extract. Note this is different to NekMesh where the parameter surf is specified and corresponds to composites rather boundaries. If bnd is not provided, all boundaries are extracted to different fields. To process this file you will need an xml file of the same region.

5.6.31 Scale a given .fld: scaleinputfld module

To scale a .fld file by a given scalar quantity, the user can run:

The argument scale=value rescales of a factor value test.fld by the factor value. The output file file-scal.fld can be processed in a similar way as described in section 5.2 to visualise the result either in Tecplot, Paraview or VisIt.

5.6.32 Time-averaged shear stress metrics: shear module

Time-dependent wall shear stress derived metrics relevant to cardiovascular fluid dynamics research can be computed using this module. They are

• TAWSS: time-averaged wall shear stress;
• OSI: oscillatory shear index;
• transWSS: transverse wall shear stress;
• TACFI: time-averaged cross-flow index;
• TAAFI: time-averaged aneurysm formation index;
• |WSSG|: wall shear stress gradient.

To compute these, the user can run:

The argument N and fromfld are compulsory arguments that respectively define the number of fld files corresponding to the number of discrete equispaced time-steps, and the first fld file which should have the form of test_id_b0.fld where the first underscore in the name marks the starting time-step file ID.

The input .fld files are the outputs of the wss module. If they do not contain the surface normals (an optional output of the wss modle), then the shear module will not compute the last metric, |WSSG|.

5.6.33 Stream function of a 2D incompressible flow: streamfunction module

The streamfunction module calculates the stream function of a 2D incompressible flow, by solving the Poisson equation

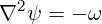
where ω is the vorticity. Note that this module applies the same boundary conditions specified for the y-direction velocity component v to the stream function, what may not be the most appropriate choice.

To use this module, the user can run

where the file test-streamfunc.fld can be processed in a similar way as described in section 5.2.

5.6.34 Boundary layer height calculation: surfdistance module

The surface distance module computes the height of a boundary layer formed by quadrilaterals (in 2D) or prisms and hexahedrons (in 3D) and projects this value onto the surface of the boundary, in a similar fashion to the extract module. In conjunction with a mesh of the surface, which can be obtained with NekMesh, and a value of the average wall shear stress, one potential application of this module is to determine the distribution of y⁺ grid spacings for turbulence calculations.

To compute the height of the prismatic layer connected to boundary region 3, the user can issue the command:

Note that no .fld file is required, since the mesh is the only input required in order to calculate the element height. This produces a file output_b3.fld, which can be visualised with the appropriate surface mesh from NekMesh.

5.6.35 Calculate vorticity: vorticity module

To perform the vorticity calculation and obtain an output data containing the vorticity solution, the user can run

where the file test-vort.fld can be processed in a similar way as described in section 5.2.

5.6.36 Computing the wall shear stress: wss module

To obtain the wall shear stres vector and magnitude, the user can run:

The option bnd specifies which boundary region to extract. Note this is different to NekMesh where the parameter surf is specified and corresponds to composites rather boundaries. If bnd is not provided, all boundaries are extracted to different fields. The addnormals is an optional command argument which, when turned on, outputs the normal vector of the extracted boundary region as well as the shear stress vector and magnitude. This option is off by default. To process the output file(s) you will need an xml file of the same region.
The output fields are wall shear stress in streamwise direction (Shear_s), normal direction (Shear_n) and magnitude of the wall shear stress vector (Shear_mag) for 2D simulations. For 3D simulations, wall shear stress in the spanwise direction (Shear_z) is also included in the output fileds. Note that the streamwise and normal directions are local at each point on the corresponding boundary.

5.6.37 Calculating the shape function Φ for an SPM case: phifile module

This FieldConvert module converts a binary .stl CAD file into .fld or .vtu/.dat files that can be used as inputs for the Smoothed Profile Method solver. Running the command:

will generate an output file geom.fld with all the information required to define a shape function Φ representing the geometry specified in geom.stl. The option scale sets the value of ξ as it is described in the Synopsis chapter of the Incompressible N-S solver. If the output file gets the extension .vtu or .dat, the module will produce a graphical representation of the shape function; however, the recommended way to proceed is to generate an .fld file and then, use FieldConvert to obtain the .vtu or .dat files if needed for visualisation purposes:

This module can also be used to produce a .fld and .vtu / .dat file of shapes defined directly in the session file through an analytical expression. In this case, the commands simplify to:

The algorithm computes an octree for the triangles that define the 3D object in the .stl file, and then loops over all the nodes of the computational mesh looking for the shortest distance to the 3D object. Since this module is currently in experimental phase, it only runs in serial and therefore its performance in computing the shape function from the .stl file is limited, especially in 3D cases. In addition to this, it is recommended to make sure that the angles between triangles are not strictly equal to 90^∘, since the algorithm will probably fail to find the real Φ function.

5.6.38 Interpolate values for a point array: wallNormalData module

To obtain the values of an array of points in the wall-normal direction, such as boundary layer profiles, the user can run:

The option bnd specifies the target boundary region, to which the input point specified by xorig will be projected as the first point in the interpolation points array. The projection direction is specified by projDir, which does not have to be a unit vector but will be automatically normalized. The input point and projetion direction must be set carefully to make sure a projected point can be found on the target boundary. In cases with curved boundaries on which multiple projected points might exist, the user can use maxDist to limit the maximum projection distance between the input point to the projected point.

After the projected point is found, this module will compute the wall-normal direction at the point, and an array of points will be set in this direction. The number of points is specified by nptsH, and the parameter d controls the distribution of the points as follows

where ξ is equally-spaced parametric parameter varying from 0 to 1; H is the distance between the first point (on the booundary) and the last point, which is specified distH; δ is given by d. This distribution is employed for 0 < δ ≤ 0.95 while δ > 0.95 for evenly-spaced distribution.

Finally, this module will interpolate the values at the points from test.fld, and save the result in test.pts.

5.6.39 Manipulating meshes with FieldConvert

FieldConvert has support for two modules that can be used in conjunction with the linear elastic solver, as shown in chapter 12. To do this, FieldConvert has an XML output module, in addition to the Tecplot and VTK formats.

The deform module, which takes no options, takes a displacement field and applies it to the geometry, producing a deformed mesh:

The displacement module is designed to create a boundary condition field file. Its intended use is for mesh generation purposes. It can be used to calculate the displacement between the linear mesh and a high-order surface, and then produce a fld file, prescribing the displacement at the boundary, that can be used in the linear elasticity solver.

Presently the process is somewhat convoluted and must be used in conjunction with NekMesh to create the surface file. However the bash input below describes the procedure. Assume the high-order mesh is in a file called mesh.xml, the linear mesh is mesh-linear.xml that can be generated by removing the CURVED section from mesh.xml, and that we are interested in the surface with ID 123.