![N
w (r,t) = A (1- (r∕R )2)+ ∑ A˜ [1- J0(i3∕2αnr-∕R-)]eiωnt
0 n=1 n J0(i3∕2α)](user-guide170x.png)
In the following the possible options are shown for the incompressible Navier-Stokes. The
Expansion section for an incompressible flow simulation can be set as for other solvers
regardless of the projection type. Here an example for a 3D simulation (for 2D simulations the
specified fields would be just u,v,p).
In case of a simulation using the Direct Solver we need to set FIELDS=u,v as the pressure
expansion order will be automatically set to fulfil the inf-sup condition. Possible choices for
the expansion TYPE are:
| Basis | TYPE |
Modal | MODIFIED |
Nodal | GLL_LAGRANGE |
Nodal SEM | GLL_LAGRANGE_SEM |
The following parameters can be specified in the SOLVERINFO section of the session
file:
EqType: sets the kind of equations we want to solve on the domain as:
Possible values are:
| Equations | EQTYPE | Dim. | Projections | Alg. |
| Steady Stokes (SS) | SteadyStokes | All | CG | VCS |
| Steady Oseen (SO) | SteadyOseen | All | CG | DS |
| Unsteady Stokes (US) | UnsteadyStokes | All | CG | VCS |
| Steady Linearised NS (SLNS) | SteadyLinearisedNS | All | CG | DS |
| Unsteady Linearised NS (ULNS) | UnsteadyLinearisedNS | All | CG | VCS,DS |
| Unsteady NS (UNS) | UnsteadyNavierStokes | All | CG,CG-DG | VCS |
SolverType: sets the scheme we want to use to solve the set of equations as
Possible values are:
| Algorithm | SolverType | Dimensions | Projections |
| Velocity Correction Scheme (VCS) | VelocityCorrectionScheme | 2D, Quasi-3D, 3D | CG, CG-DG |
| Smoothed Profile Method (SPM) | SmoothedProfileMethod | 2D, Quasi-3D, 3D | CG, CG-DG |
| VCS with weak pressure | VCSWeakPressure | 2D, Quasi-3D, 3D | CG, CG-DG |
| Direct solver | CoupledLinearisedNS | 2D, Quasi-3D | CG |
Driver: this specifies the type of problem to be solved:
| Driver | Description | Dimensions | Projections |
Standard | Time integration of the equations | All | CG, DG |
SteadyState | Steady-state solver (see Sec. 11.1.5) | All | CG, DG |
Projection: sets the Galerkin projection type as
Possible values are:
| Galerkin Projection | Projection | Dimensions | Equations | Algorithms |
| Continuous (CG) | Continuous | All | All | All |
| Discontinuous (DG) | DisContinuous | All | ... | ... |
| Mixed CG and DG (CG-DG) | Mixed_CG_Discontinuous | 2D,3D | just UNS | VCS-substepping |
TimeIntegrationScheme: sets the time integration as
Possible values are
| Time-Integration Scheme | Method | Order | Dimensions | Equations | Projections |
| IMEX Order 1 | IMEX | 1 | all | US, UNS | CG |
| IMEX Order 2 | IMEX | 2 | all | US, UNS | CG |
| IMEX Order 3 | IMEX | 3 | all | US, UNS | CG |
| Backward Euler | BackwardEuler | 1 | all | US, UNS | CG-DG |
| BDF Order 1 | BDFImplicit | 1 | all | US, UNS | CG-DG |
| BDF Order 2 | BDFImplicit | 2 | all | US, UNS | CG-DG |
Extrapolation: Specify the extrapolation method (standard or substepping) to be used
in velocity correction scheme. Essentially this activates the sub-stepping routine which
requires the mixed CG-DG projection
Possible values are SubStepping or Standard with “Standard” being the default value if
nothing is specifiied.
SubStepIntScheme: choose the substep DG time integration scheme so that a different
order schems can be used as compared to the overal time integraiton scheme.
Possible values are
| Time-Integration Scheme | SubStepIntScheme |
| ForwardEuler, Order 1 | ForwardEuler, Order 1 |
| RungeKutta, Order 2 | RungeKutta, Variant SSP, Order 2 |
This option is useful if you wish to use an overall scheme that is first order accurate for example with TimeIntegrationScheme as BDFImplicit Order 1 but using a second order RungeKutta, Variant SSP, Order 2 for greater stability in the substep.
GlobalSysSoln: sets the approach we use to solve the the linear systems of the type
Ax = b appearing in the solution steps, such as the Poisson equation for the pressure in
the splitting-scheme. It can be set as
Possible values are
| System solution | GlobalSysSoln | Parallel |
| Direct Solver (DS) | DirectFull | just quasi-3D |
| DS with Static Condensation | DirectStaticCond | just Quasi-3D |
| DS with Multilevel Static Condensation | DirectMultiLevelStaticCond | just Quasi-3D |
| Iterative Solver (IS) | IterativeFull | just Quasi-3D |
| IS with Static Condensation | IterativeStaticCond | quasi-3D |
| IS with Multilevel Static Condensation | IterativeMultiLevelStaticCond | quasi-3D |
Default values are DirectMultiLevelStaticCond in serial and IterativeStaticCond in
parallel.
SmoothAdvection: activates a stabilization technique which smooths the advection term
using the pressure inverse mass matrix. It can be used just in combination with nodal
expansion basis for efficiency reasons.
SpectralVanishingViscosity: activates a stabilization technique which increases the
viscosity on the modes with the highest frequencies.
In a Quasi-3D simulation, this will affect both the Fourier and the spectral/hp expansions.
To activate them independently, use SpectralVanishingViscositySpectralHP and
SpectralVanishingViscosityHomo1D.
There are three spectral vanishing viscosity kernels available:
| SVV Kernel | SpectralVanishingViscosity |
| Exponential Kernel | True |
| Power Kernel | PowerKernel |
| DG Kernel | DGKernel |
The Exponential kernel is based on the work of Maday et al. [29], its extension to 2D can be found in [22]. A diffusion coefficient can be specified which defines the base magnitude of the viscosity; this parameter is scaled by h∕p. SVV viscosity is activated for expansion modes greater than the product of the cut-off ratio and the expansion order. The Power kernel is a smooth function with no cut-off frequency; it focusses on a narrower band of higher expansion modes as the polynomial order increases. The cut-off ratio parameter for the Power kernel corresponds to the power ratio, see Moura et al. [31]. The DG-Kernel is an attempt to match the dissipation of CG-SVV to DG schemes of lower expansion orders. This kernel does not require any parameters although the diffusion coefficient can still be modified.
GJPStabilisation: activates the gradient jump penalty[32] stabilization technique. The
GJP is less dissipative than the spectral vanishing viscousity (SVV) stabilisation and
gives a better turbulent structures specially when the simulaiton is under-resolved or in
other words when the polynomial order is low. It is expected that with increasing the
polynomial order and approaching towards a resolved solution both SVV and GJP
stabilisation solutions approaches each other. Since the GJP is less dissipative than the
SVV, it means that it probably requires a smaller Δt for the stable solution. Further,
GJP only affects the spectral/hp discretisations and doesn’t have any stabilisation effect
on the Fourier discritisation. This means that in the Quasi-3D simulations, if GJP is
activated we still needs to use the SpectralVanishingViscousityHomo1D to stablise the
solution in the spanwise direction which is discretised using the Fourier method.
For the 2D and full 3D problems, GJP stabilisation should suffices though.
Another option for the GJP stabilisation is to use Explicit for its value instead of
SemiImplicit. If the Explicit value is set, there is an additional option that can be set
for the explicit GJP stabilisation in the solver info as follwos.
Using the GJPNormalVelocity, the GJP formulation will uses the average velocity
normal to the edge/face as the velocity scaling of jump term.
DEALIASING: activates the 3/2 padding rule on the advection term of a Quasi-3D
simulation.
SPECTRALHPDEALIASING: activates the spectral/hp dealiasing to stabilize the simulation.
This method is based on the work of Kirby and Sherwin [7].
The following parameters can be specified in the PARAMETERS section of the session
file:
TimeStep: sets the timestep for the integration in time formula.
NumSteps: sets the number of time-steps.
IO_CheckSteps: sets the number of steps between successive checkpoint files.
IO_InfoSteps: sets the number of steps between successive info stats are printed
to screen.
Kinvis: sets the cinematic viscosity coefficient formula.
SubStepCFL: sets the CFL safety limit for the sub-stepping algorithm (default
value = 0.5).
MinSubSteps: perform a minimum number of substeps in sub-stepping algorithm
(default is 1).
MaxSubSteps: perform a maxmimum number of substeps in sub-stepping algorithm
otherwise exit (default is 100).
SVVCutoffRatio: sets the ratio of Fourier frequency not affected by the SVV
technique (default value = 0.75, i.e. the first 75% of frequency are not damped).
SVVDiffCoeff: sets the SVV diffusion coefficient (default value = 0.1 (Exponential
and Power kernel), 1 (DG-Kernel)).
GJPJumpScale: This is a parameter that scales all of the jump terms in the GJP
stabilisation formualtion. The default value GJPJumpScale=1.
IO_CFLWriteFld: sets a treshold value for the CFL number. If CFL exceeds this
value, the flow field is written to file (only once). This is useful for debugging
purposes, allowing to visually inspect a flow field that is becoming unstable.
IO_CFLWriteFldNumSteps: sets the number of timesteps after
which IO_CFLWriteFld becomes operational. This avoids writing the flow field at
the beginning of a simulation when initialising a new geometry.
It is possible to define the time-dependent Womersley velocity profile for pulsatile flow in a pipe. The modulation of the velocity profile is based on the desired peak or centerline velocity which can be represented by a Fourier expansion Umax = A(ωn)eiωnt where A are the Fourier modes and ω the frequency. The womersely solution is then defined as:
![N
w (r,t) = A (1- (r∕R )2)+ ∑ A˜ [1- J0(i3∕2αnr-∕R-)]eiωnt
0 n=1 n J0(i3∕2α)](user-guide170x.png)
where the womersley number α is defined:
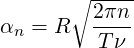
and 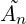 (n = 1 : N)are the Fourier coefficients scaled in the following way:
(n = 1 : N)are the Fourier coefficients scaled in the following way:
![1
A˜n = 2An ∕[1- J-(i3∕2α-)]
0](user-guide173x.png)
The Womersley velocity profile is implemented in the following way:
A file containing the Fourier coefficients, Ã, must be in the directory where the solver is called
from. The name of the file is defined by the string given in the attribute USERDEFINEDTYPE
after the “:” and contains the real and imaginary coefficients. This file has the format
Each value of à is provided in the FOURIERCOEFFS section and provided as separate entries
containing the real and imaginary components, i.e. the mean component provided above is
0.600393641193,0.0.
Similarly in the WOMPARAMS section the key parameters of the boundary condition are also
provided as:
RADIUS is the radius of the boundary.
PERIOD is the cycle time period,
AXISNORMAL defines the normal direction to the boundary,
AXISPOINT defines a coordinate in the boundary centre,
This force type allows the user to solve the interaction system of an incompressible fluid flowing past a flexible moving bodies [36]. By this forcing function, one can eliminate the difficulty of moving mesh by using body-fitted coordinates, so that an additional acceleration term(i.e., forcing term) is introduced to the momentum equations by the non-inertial transform from the deformed and moving coordinate system to non-deformed and stationary one.
Available options of the motion type for the moving body include free, constrained
and forced vibrations, which can be specified in the TIMEINTEGRATIONSCHEME and
SOLVERINFO section. The free type of motion allows the body to move in both streamwise
and crossflow directions, while the constrained type limits the motion only in the
crossflow direction. For the forced type, the vibration profiles of the body should be
specified as a given function or read from input file in MovingBody section. For
example:
A moving body type boundary condition should be specified in BOUNDARYCONDITIONS for the
velocities on the moving body,
For the simulation of low mass ratio, there is an option to activate fictitious mass method for
stabilizing explicit coupling between the fluid solver and structural dynamic solver. Here
we need to specify the values of fictitious mass and damping in PARAMETERS, for
example,
A filter called MovingBody is encapsulated in this module to evaluate the aerodynamic forces
along the moving body surface. The forces for each computational plane are projected along
the Cartesian axes and the pressure and viscous contributions are computed in each
direction.
The following parameters are supported:
| Option name | Required | Default | Description |
OutputFile | ✗ | session | Prefix of the output filename to which the forces are written. |
Frequency | ✗ | 1 | Number of timesteps after which output is written. |
Boundary | ✓ | - | Boundary surfaces on which the forces are to be evaluated. |
To enable the filter, add the following to the FORCE tag::
During the execution a file named DragLift.fce will be created and the value of the
aerodynamic forces on boundary 0, defined in the GEOMETRY section, will be output every 10
time steps.evaluates the aerodynamic forces along the moving body surface. The forces for
each computational plane are projected along the Cartesian axes and the pressure and viscous
contributions are computed in each direction.
Also, to use this module a MAPPING needs to be specified, as described in section 11.6. In the
case of free and constrained motion presented here, the functions defined by the mapping act
as initial conditions. Also, when using the MovingBody forcing, it is not necessary to set the
TIMEDEPENDENT property of the mapping.
The following filters are supported exclusively for the incompressible Navier-Stokes solver. Further filters from section 3.4 are also available for this solver.