NekMesh is designed to provide a pipeline approach to mesh generation. To do this, we break
up tasks into three different types. Each task is called a module and a chain of modules
specifies the pipeline.
The figure below depicts how these might be coupled together to form a pipeline:
On the command line, we would define this as:
Process modules can also have parameters passed to them, that can take arguments, or not.
To list all available modules use the -l command line argument:
and then to see the options for a particular module, use the -p command line argument:
-p option. Input modules should be preceded
by in:, processing modules by proc: and output modules by out:.
Input and output modules use file extension names to determine the correct module to use. Not every module is capable of reading high-order information, where it exists. The table below indicates support currently implemented.
| Format | Extension | High-order | Notes |
| Gmsh | msh | ✓ | Only reads nodes, elements and physical groups (which are mapped to composites). File format versions 2.x and 4.x currently supported. |
| Nektar | rea | ✓ | Reads elements, fluid boundary conditions. Most curve types are unsupported: high-order information must be defined in an accompanying .hsf file. |
| Nektar++ | xml | ✓ | Fully supported. |
| PLY | ply | ✗ | Reads only the ASCII format.. |
| Semtex | sem | ✓ | Reads elements and boundary
conditions. In order
to read high-order information,
run |
| Star-CCM+ | dat | ✗ | Star outputs plt file which currently needs to be coverted to ascii using Tecplot. Reads mesh only, only support for quads and triangles (2D) and hexes, prisms, tetrahedra (3D). |
| Star-CCM+ | ccm | ✗ | Reads start ccm format. Reads mesh only, only support for quads and triangles (2D) and hexes, prisms, tetrahedra (3D). Requires NEKTAR_USE_CCM option to be activated in cmake and then requires ccmio library to be compiled by user. |
| VTK | vtk | ✗ | Experimental support. Only ASCII triangular data is supported. |
Note that you can override the module used on the command line. For example, Semtex
session files rarely have extensions. So for a session called pipe-3d we can convert this using
the syntax
The NekMesh input module also has an option to re-process all composites. By default only
composites are reprocessed. However when extracting a smaller mesh from a larger mesh
definition by redefining the composite of volumetric elements you can force the edges
and/or faces to be reprocessed removing the definition of any edges and/or faces
not required in the smaller mesh. This option is called processall and has the
syntax
Typically, mesh generators allow physical surfaces and volumes to contain many element
types; for example a cube could be constructed from a mixture of hexes and prisms. In
Nektar++, a composite can only contain a single element type. Whilst the converter will
attempt to preserve the numbering of composites from the original mesh type, sometimes a
renumbering will occur when a domain contains many element types. For example, for a
domain with the tag 150 containing quadrilaterals and triangles, the Gmsh reader will print a
notification along the lines of:
The resulting file therefore has two composites of IDs 150 and 151 respectively, containing the
triangular and quadrilateral elements of the original mesh. We note there is one exception to
this convention in three-dimensional meshes where a face composite can contain both
triangular and quadrilateral elements.
Typically a NekMesh call requires both an input and output module to be called, however, by
specifying the output file name or file extension as stdout no output file will be created. This
option is typically used for mesh statistics processing or inspecting composite values etc. An
example call would be:
or
The following output formats are supported:
| Format | Extension | High-order | Notes |
| Gmsh | msh | ✓ | High-order hexes, quads, tetrahedra and triangles are supported up to arbitrary order. Prisms supported up to order 4, pyramids up to order 1. |
| Nektar++ | xml | ✓ | Most functionality supported. |
| HDF5 | nekg | ✓ | Most functionality supported. |
| VTK | vtk | ✗ | Outputs mesh only, supports line segments in 1D, triangles and quadrilaterals in 2D and tetrahedra, hexahedra, prisms and pyramids in 3D. The VTK legacy format and XML format, both compressed and uncompressed, are supported. Requires NEKTAR_USE_VTK option to be activated in cmake. |
Note that for Gmsh, it is highly likely that you will need to experiment with the source code in
order to successfully generate meshes since robustness is not guaranteed.
The default for xml and vtk is into binary data which has been converted into base64. If you
wish to see an ascii output you need to specify the output module option uncompress. For the
uncompressed xml the user can execute:
If the user wishes to obtain the vtk output in the legacy format, the output module option
legacy should be specified by executing:
Finally, both the Gmsh and Nektar++ output modules support an order parameter, which
allows you to generate a mesh of a uniform polynomial order. This is used in the same manner
as the above, so that the command
will generate an order 7 Gmsh mesh. In the rest of these subsections, we discuss the various
processing modules available within NekMesh.
It is possible to use FieldConvert to extract a smaller region of a mesh from a larger mesh using the “-r xmin,xmax,ymin,ymax,zmin” range option, e.g.
However this will not provide a composite of he faces on the boundary if they were not part of
the original boundary composites of the original bigMesh.xml. These can however be
recovered by an output module option chkbndcomp in NekMesh. To do this one should specify
this will then add a composite for any face that is on the boundary and not part of an existing
boundary condition and put it into a composite with id=9999. This capability is currently
only set up for 3D meshes
NekMesh and all solvers within Nektar++ - along with subsequent FieldConvert modules - also support the HDF5 format. This allows for faster loading of geometries and meshes within each solver - and is a significant improvement over the XML format. HDF5 is recommended input format for any larger cases.
Converting from XML to HDF5 is a simple task that only requires the one NekMesh command:
This will create two files HDF5Mesh.xml and HDF5Mesh.nekg which are both needed in the
same directory to run the simulation. An additional flag in the session file is required, ensuring
it is placed before the expansion list being:
HDF5 also has the additional advantage of ensuring the mesh and session file are split - which
allows for easy ammending of the session file - whilst allowing for use of FieldCovnert modules
that require only 1 XML input file - rather than having to concatenate the session and mesh
XML files. Solvers and any FieldConvert modules can be run by referencing only the session
file after the GEOMETRY tag is included.
Often one wants to visualise surfaces of a 3D mesh, or extract the values of variables on the
surface and visualise them. To support this, NekMesh can extract two-dimensional surfaces
which can be visualised using FieldConvert in order to extract the value of a 3D field on a
given surface.
As an example, we can extract composite surfaces 2 and 3-5 from a mesh using the extract
module:
If you also wish to have the boundaries of the extracted surface detected add the detectbnd
option
which will produce new composites for the extracted boundary.
To detect elements with negative Jacobian determinant, use the jac module:
To get a detailed list of elements which have negative Jacobians, one may use the list option:
and to extract the elements for the purposes of visualisation within the domain, use the
extract boolean parameter:
To turn off curvature associated with negative jacobians one can try to use the linearise
module:
This option will remove all high order curvature on all element types with singular jacobians.
Where high-order information is not available (e.g. when using meshes from imaging software),
various techniques can be used to apply a smoothing to the high-order element. In NekMesh we
use spherigons, a kind of patch used in the computer graphics community used for efficiently
smoothing polygon surfaces.
Spherigons work through the use of surface normals, where in this sense ‘surface’ refers to the
underlying geometry. If we have either the exact or approximate surface normal at each given
vertex, spherigon patches approximate the edges connecting two vertices by arcs of a circle. In
NekMesh we can either approximate the surface normals from the linear elements which
connect to each vertex (this is done by default), or supply a file which gives the surface
normals.
To apply spherigon patches on two connected surfaces 11 and 12 use the following command:
If the two surfaces "11" and "12" are not connected, or connect at a sharp edge which is C0 continuous but not C1 smooth, use two separate instances of the spherigon module.
This is to avoid the approximated surface normals being incorrect at the edge.
If you have a high-resolution mesh of the surfaces 11 and 12 in ply format it can be used to
improve the normal definition of the spherigons. Run:
This can be useful, for example, when meshing the Leading edge of an airfoil. Starting from a linear mesh (left figure) the spherigon patches curve the surface elements producing leading edge closer to the underlying geometry:
When using periodic boundary conditions, the order of the elements within the boundary composite determines which element edges are periodic with the corresponding boundary composite.
To facilitate this alignment, NekMesh has a periodic alignment module which attempts to
identify pairs of mutually periodic edges. Given two surfaces surf1 and surf2, which for
example correspond to the physical surface IDs specified in Gmsh, and an axis which defines
the periodicity direction, the following command attempts to reorder the composites:
Here the surfaces with IDs 11 and 12 will be aligned normal to the y-axis and the surfaces 13 and 14 will be aligned normal to the z-axis.
Note that this command cannot perform magic – it assumes that any given edge or face lying on the surface is periodic with another face on the opposing surface, that there are the same number of elements on both surfaces, and the corresponding edge or face is the same size and shape but translated along the appropriate axis.
When using periodic boundary conditions that are rotationally aligned the following rotational options should be applied:
where rot specifies the rotation angle in radians from surf1 to surf2 about the axis specified
by dir (i.e. the “x” axis in this example).
The rotation/translation is assumed to be exact within a relative tolerance. An optional
factor, which is used to scale the tolerance, tolfact can also be specified. The default
tolerance factor is 4, and it needs to be tolfact ≥ 1. For example:
In 3D, where prismatic or tetrahedral elements are connected to one or both of the surfaces,
additional logic is needed to guarantee connectivity in the XML file. In this case we append
the orient parameter:
orient is that it throws away all high-order
information and works only on the linear element. This can be gotten around if you are just
doing e.g. spherigon patches by running this peralign module before the spherigon
module.
Often it is the case that one can generate a coarse boundary layer grid of a mesh. NekMesh has
a method for splitting prismatic and hexahedral elements into finer elements based on the
work presented in [33] and [34]. You must have a prismatic mesh that is O-type
– that is, you can modify the boundary layer without modifying the rest of the
mesh.
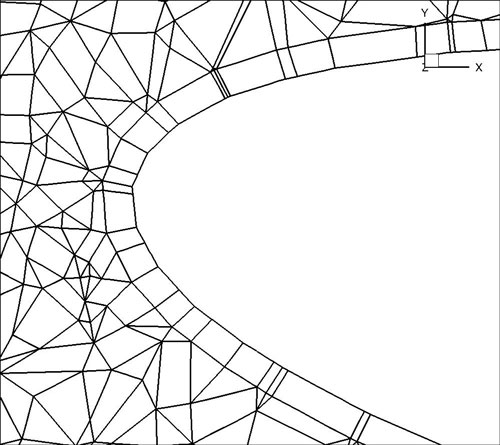
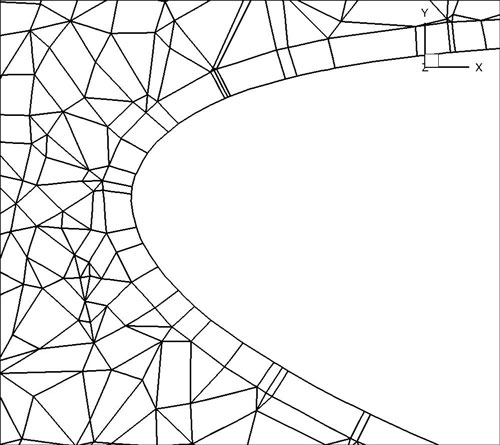
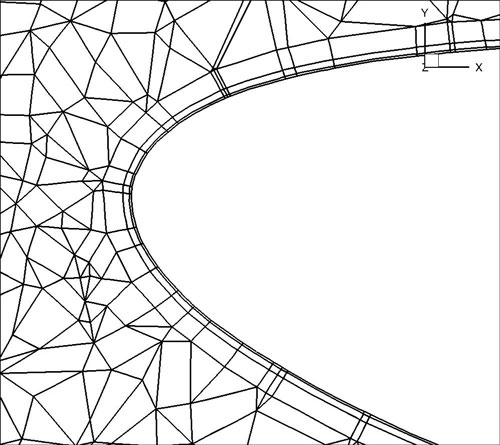
Given n layers, and a ratio r which defines the relative heights of elements in different layers, the method works by defining a geometric progression of points
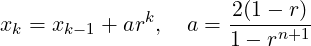
in the standard segment [-1,1]. These are then projected into the coarse elements to construct a sequence of increasingly refined elements, as depicted in figure 4.4.
To split a prism boundary layer on surface 11 into 3 layers with a growth rate of 2 and 7 integration points per element use the following command:

r=sin(x). In this case the function should be sufficiently smooth to
prevent the elements self-intersecting.
Generating accurate high-order curved geometries in Gmsh is quite challenging. This
module processes an existing linear cylindrical mesh, with axis aligned with the
z-coordinate axis, to generate accurate high-order curvature information along the
edges.
The module parameters are:
surf: Surface on which to apply curvature. This should be the outer surface of the
cylinder.
r: Radius of the cylinder.
N: Number of high-order points along each element edge.
The ability to remove all the high-order information in a mesh can be useful at times when mesh generation is tricky or impossible in the presence of curvature
To do this in NekMesh use the command:
The output will contain only the linear mesh information, all curved information is removed. Alternatively
attempts to remove curvature from elements only where necessary. This is a simple algorithm
that removes curvature from invalid elements and repeats until all elements are valid. Either
all or invalid must be specified.
all: remove curvature from all elements.
invalid: remove curvature from invalid elements.
prismonly: consider only prisms when removing curvature. This is useful in the
presence of a prismatic boundary layer.
When the mesh is three-dimensional and comprised of a prismatic boundary layer with tetrahedra in the interior of the domain, this module extracts the prismatic elements only, and constructs a boundary region for the interface between the tetrahedra and prisms. This is useful in, for example, the study of aortic flows, where the prismatic boundary layer can be extracted and refined to study unsteady advection-diffusion problems on a more refined grid inside the boundary layer.
To use this module you therefore use the command:
There are no configuration options for this module, as it is highly specific to a certain class of meshes.
Some mesh formats lack the ability to identify boundaries of the domain they discretise.
NekMesh has a rudimentary boundary identification routine for conformal meshes, which will
create a composite of edges (2D) or faces (3D) which are connected to precisely one element.
This can be done using the detect module:
This module imposes curvature on a surface given a scalar function z = f(x,y). For example, if on surface 1 we wish to apply a surface defined by a Gaussian z = exp[-(x2 + y2)] using 7 quadrature points in each direction, we may issue the command
It is quite possible that a mesh contains some sort of hanging entity or element connectivity error. The check link module is a fast check that, a) elements are correctly connected and b) the boundary entities (composites) match the interior domain:
This module should be added to the module chain if the user suspects there may be a mesh issue. The module will print a warning if there is a connectivity error.
This module allows a 2D mesh, quads, triangles or both, to be extruded in the z direction to make a simple 3D mesh made of prisms and hexahedra. It is also capable of extruding the high-order curvature within the 2D mesh. The module requires two parameters:
length which determines how long the z extrusion will be and layers, the number of elements in the z direction.
This module can correct invalid and improve the quality of elements in high-order meshes by applying curvilinear deformation to the interiors of domains. It achieves this by solving a solid mechanics system which, using variational calculus has been cast is a non-linear energy optimsation problem. It is basis of the work in [46].
It works by considering the boundary (curved) mesh entities to be fixed and moving the interior nodes to a lower energy configuration. This new configuration in most scenarios is a higher quality mesh. The energy is evaluated depending on which functional is chosen. We find hyperleastic to be the most reliable but it can also model the mesh and a linearelastic solid as well as functionals based on the Winslow equation and the distortion method proposed by Roca et al. [14].
There are a large number of options which can be viewed using the help function but the basic usage is:
where type can be hyperelastic, linearelastic, winslow or roca.
This module can deform an existing mesh by using the variational optimiser presented above. A file must be provided that contains a list of points and a scaling value for each of them. This scaling factor is then used to target an element size based on the initial size of the element. Scaling values are interpolated throughout the domain based on the interpolation method of the main library. The file should look like
where the first three columns are x, y, z and the last column is the scaling factor.
The call is identical to the variational optimisation module above:
where subiter is an additional parameter to the variational optimiser that defines the
frequency at which individual elements update their target scaling based on their latest
location in the domain. subiter should be a scalar and is the number of steps between
updates. It is often recommended to run r-adaptation on a linear mesh for stability and
performance reasons. Note also that the mesh must have CAD information in order for nodes
to slide on curves and surfaces.
This module can take any linear mesh, providing that it is a close representation of the CAD and project the boundary of the mesh onto the CAD. This will curve the surface of the mesh. The method has a number of failsafes ensuring that even bad CAD or poor linear meshes should be able to be curved to some degree. If the method encounters an issue, such as the linear mesh being a large distance from the CAD, it will simply leave that element straight sided. A well made CAD model and accurate linear mesh should be curved with little issue.
The module needs to be informed of the CAD file to project the mesh to and the order at which to curve the surface: