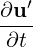 + L(U,u′) = -∇p + ν∇2u′,
+ L(U,u′) = -∇p + ν∇2u′,Stability analyses of incompressible flow involves solving the linearised Navier-Stokes equations
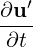 + L(U,u′) = -∇p + ν∇2u′, + L(U,u′) = -∇p + ν∇2u′, |
where L is a linear operator, its adjoint form, or both. The evolution of the linearised Navier-Stokes operator, which evolves a solution from an initial state to a future time t, can be written as
| u(t) = A(t)u(0). |
The adjoint evolution operator is denoted as A*. This section details the additional configuration options, in addition to the standard configuration options described earlier, relating to performing this task.
Eqtype: sets the type of equation to solve. For linear stability analysis this must be set
to
| Equation Type | Dimensions | Projections | Algorithms |
| UnsteadyNavierStokes | 2D, Quasi-3D | Continuous | VCS,DS |
EvolutionOperator: sets the choice of the evolution operator:
Nonlinear (standard non-linear Navier-Stokes equations).
Direct (A – linearised Navier-Stokes equations).
Adjoint (A* – adjoint Navier-Stokes equations).
TransientGrowth (A*A – transient growth evolution operator).Driver: specifies the type of problem to be solved:
Standard (normal time integration of the equations)
ModifiedArnoldi (computations of the leading eigenvalues and eigenmodes
using modified Arnoldi method)
Arpack (computations of eigenvalues/eigenmodes using Implicitly Restarted
Arnoldi Method (ARPACK) ).ArpackProblemType: types of eigenvalues to be computed (for Driver Arpack
only)
LargestMag (eigenvalues with largest magnitude).
SmallestMag (eigenvalues with smallest magnitude).
LargestReal (eigenvalues with largest real part).
SmallestReal (eigenvalues with smallest real part).
LargestImag (eigenvalues with largest imaginary part).
SmallestIma (eigenvalues with smallest imaginary part ).Homogeneous: specifies the Fourier expansion in a third direction (optional)
1D (Fourier spectral method in z-direction).ModeType: this specifies the type of the quasi-3D problem to be solved.
MultipleModes (stability analysis with multiple modes, HomModesZ sets
number of modes).
SingleMode (BiGlobal Stability Analysis: full-complex mode. Overrides
HomModesZ to 1.).
HalfMode (BiGlobal Stability Analysis: half-complex mode u.Re v.Re w.Im
p.Re).Homogeneous results with FieldConvert you can use
--output-points-hom-z to set output number of modes to a desired value. To process
results obtained with HalfMode you can convert to SingleMode using FieldConvert
module halfmodetofourier.
The following parameters can be specified in the PARAMETERS section of the session
file:
kdim: sets the dimension of the Krylov subspace κ. Can be used with:
ModifiedArnoldi and Arpack. Default value: 16.
evtol: sets the tolerance of the iterative eigenvalue algorithm. Can be used with:
ModifiedArnoldi and Arpack. Default value: 1 × 10-6.
nvec: sets the number of converged eigenvalues sought. Can be used with:
ModifiedArnoldi and Arpack. Default value: 2.
nits: sets the maximum number of Arnoldi iterations to attempt. Can be used
with: ModifiedArnoldi and Arpack. Default value: 500.
realShift: provide a real shift to the direct solver eigenvalue problem by the
specified value to improve convergence. Can be used with: Arpack only.
imagShift: provide an imaginary shift to the direct solver eigenvalue problem by
the specified value to improve convergence. Can be used with: Arpack only.
LZ: sets the length in the spanswise direction Lz. Can be used with Homogeneous
set to 1D. Default value: 1.
HomModesZ: sets the number of planes in the homogeneous directions. Can be used
with Homogeneous set to 1D and ModeType set to MultipleModes.
N_start: sets the start number of temporal slices for Floquet stability analysis.
Default value: 0.
N_skip: sets the number skip of temporal slices for Floquet stability analysis.
Default value: 1.
N_slices: sets the
number of temporal slices for Floquet stability analysis. Files sequence N_start,
N_start + N_skip, ..., N_start + N_skip * (N_slices-1) will be loaded.
BaseFlow_interporder: sets the interpolation order of temporal slices for Floquet
stability analysis. If BaseFlow_interporder < 2, the baseflow is taken as periodic
and trigonometric functions are used for interpolation. It should be noted that the
file N_start + N_skip * N_slices is at t = period and should not be loaded for
the periodic case. If BaseFlow_interporder >= 2, the flow is taken as aperiodic
and Lagrange interpolation is used. In this case, the file N_start + N_skip *
(N_slices-1) is at t = period and should be loaded. Default value: 0.
period: sets the time span (if BaseFlow_interporder >= 2) or period (if
BaseFlow_interporder < 2) of the base flow. Default value: 1.
When using the direct solver for stability analysis it is necessary to specify a Forcing function “StabilityCoupledLNS” in the form:
This is required since we need to tell the solver to use the existing field as a forcing function to the direct matrix inverse as part of the Arnoldi iteration.
NEKTAR/solvers/IncNavierStokesSolver/Tests. See for example the files
PPF_R15000_ModifiedArnoldi_Shift.tst and PPF_R15000_3D.xml noting that some
parameters are specified in the .tst files.