[next] [prev] [prev-tail] [tail] [up]

13.1 Synopsis

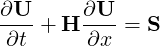
1D modelling of the vasculature (arterial network) represents and insightful and efficient tool for tackling problems encountered in arterial biomechanics as well as other engineering problems. In particular, 3D modelling of the vasculature is relatively expensive. 1D modelling provides an alternative in which the modelling assumptions provide a good balance between physiological accuracy and computational efficiency. To describe the flow and pressure in this network we consider the conservation of mass and momentum applied to an impermeable, deformable tube filled with an incompressible fluid, the nonlinear system of partial differential equations presented in non-conservative form is given by

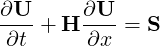∂U ∂U ----+ H ----= S ∂t ∂x
(13.1)

[U ] [ U A] [ 0 ] U = , H = ∂P- , S = 1( f- ) A ρ∂A U ρ A - s

in which A is the Area (related to pressure), x is the axial coordinate along the vessel, U(x,t) the axial velocity, P(x,t) is the pressure in the tube, ρ is the density and finally f the frictional force per unit length. The unknowns in Eq. 13.1 are U,A and P; hence, we must provide an explicit algebraic relationship to close this system. Typically, closure is provided by an algebraic relationship between A and P. For a thin, viscoelastic tube this is given by

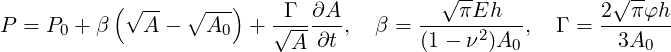√-- √ -- (√ -- ∘ ---) -Γ-∂A- ---πEh---- 2--πφh- P = P0 + β A - A0 + √A- ∂t , β = (1 - ν2)A0 , Γ = 3A0
(13.2)

where P0 is the external pressure, A0 is the initial cross-sectional area, E is the Young’s modulus, h is the vessel wall thickness, ν is the Poisson’s ratio, and φ is the wall viscosity. An empirical law has also been implemented that incorporates strain-stiffening through the parameter α [1]:

√ --- [ ( )] β--A0- A-- √Γ-∂A- P = P0 - 2α ln 1- α ln A0 + A ∂t .
(13.3)

Application of Riemann’s method of characteristics to Eqs. (13.1) and (13.2) indicates that velocity and area are propagated through the system by forward and backward travelling waves. These waves are reflected and within the network by appropriate treatment of interfaces and boundaries. In the following, we will explain the usage of the blood flow solver on the basis of a single-artery problem and also on an arterial network consisting of 55 arteries.

[next] [prev] [prev-tail] [front] [up]