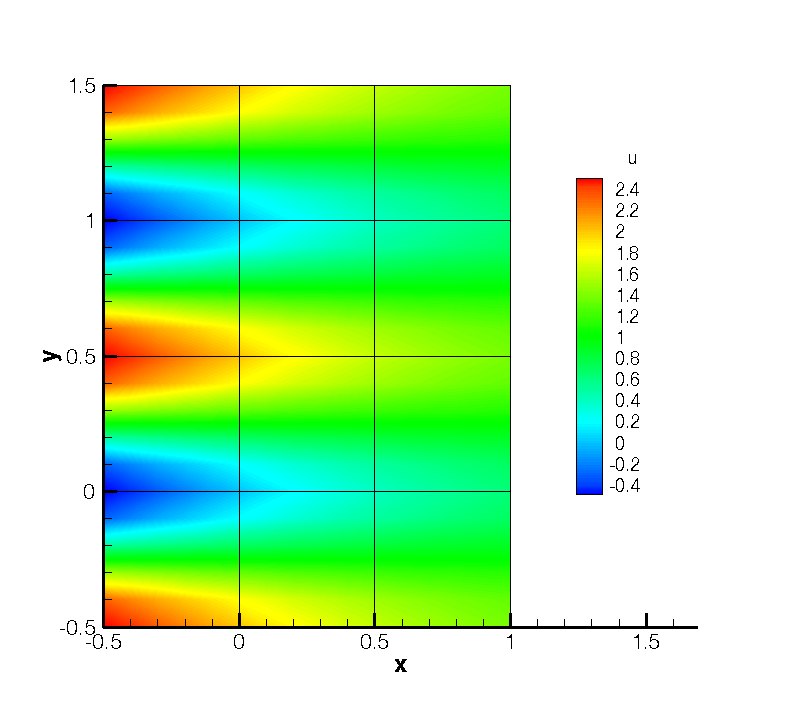
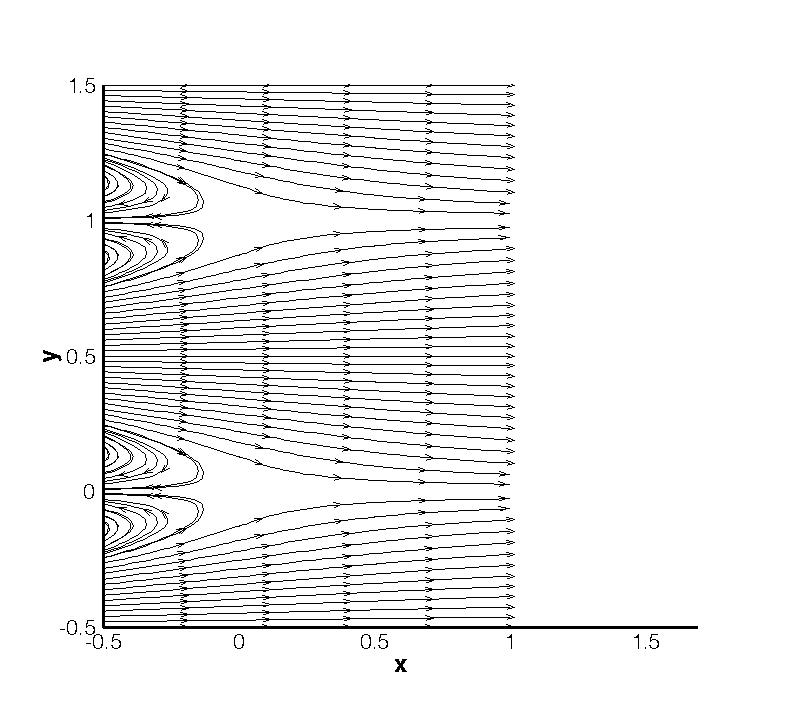
This example demonstrates the use of the velocity correction o solve the 2D Kovasznay flow at Reynolds number Re = 40. In the following we will numerically solve for the two dimensional velocity and pressure fields with steady boundary conditions.
The input for this example is given in the example file KovaFlow_m8.xml. The mesh consists
of 12 quadrilateral elements.
We will use a 7th-order polynomial expansions (N = 8 modes) using the modified Legendre basis and therefore require the following expansion definition.
1<EXPANSIONS> 2 <E COMPOSITE="C[0]" NUMMODES="8" FIELDS="u,v,p" TYPE="MODIFIED" /> 3</EXPANSIONS>
We next specify the time integration scheme and solver information for our problem. In particular, we select the velocity correction scheme formulation, using a continuous Galerkin projection. For this scheme, an implicit-explicit time-integration scheme must be used and we choose one of second order.
1 <TIMEINTEGRATIONSCHEME> 2 <METHOD> IMEX </METHOD> 3 <ORDER> 2 </ORDER> 4 </TIMEINTEGRATIONSCHEME> 5 6 <SOLVERINFO> 7 <I PROPERTY="EQTYPE" VALUE="UnsteadyNavierStokes" /> 8 <I PROPERTY="SolverType" VALUE="VelocityCorrectionScheme" /> 9 <I PROPERTY="AdvectionForm" VALUE="Convective" /> 10 <I PROPERTY="Projection" VALUE="Galerkin" /> 11 </SOLVERINFO>
The key parameters are listed below. Since the problem is unsteady we prescribe the time step
and the total number of time steps. We also know the required Reynolds number, but we must
prescribe the kinematic viscosity to the solver. We first define a dummy parameter for the
Reynolds number, and then define the kinematic viscosity as the inverse of this. The value of λ
is used when defining the boundary conditions and exact solution. Note that PI is a
pre-defined constant.
1<PARAMETERS> 2 <P> TimeStep = 0.001 </P> 3 <P> NumSteps = 100 </P> 4 <P> Re = 40 </P> 5 <P> Kinvis = 1/Re </P> 6 <P> LAMBDA = 0.5*Re-sqrt(0.25*Re*Re+4*PI*PI)</P> 7</PARAMETERS>
We choose to impose a mixture of boundary condition types as defined below.
1<BOUNDARYCONDITIONS> 2 <REGION REF="0"> 3 <D VAR="u" VALUE="1-exp(LAMBDA*x)*cos(2*PI*y)" /> 4 <D VAR="v" VALUE="(LAMBDA/2/PI)*exp(LAMBDA*x)*sin(2*PI*y)" /> 5 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 6 </REGION> 7 <REGION REF="1"> 8 <D VAR="u" VALUE="1-exp(LAMBDA*x)*cos(2*PI*y)" /> 9 <D VAR="v" VALUE="(LAMBDA/2/PI)*exp(LAMBDA*x)*sin(2*PI*y)" /> 10 <D VAR="p" VALUE="0.5*(1-exp(2*LAMBDA*x))" /> 11 </REGION> 12 <REGION REF="2"> 13 <N VAR="u" VALUE="0" /> 14 <D VAR="v" VALUE="0" /> 15 <N VAR="p" VALUE="0" /> 16 </REGION> 17</BOUNDARYCONDITIONS>
Initial conditions are obtained from the file KovaFlow_m8.rst, which is a Nektar++ field file.
This is the output of an earlier simulation, renamed with the extension rst to avoid being
overwritten, and is used in this case to reduce the integration time necessary to obtain the
steady flow.
1<FUNCTION NAME="InitialConditions"> 2 <F FILE="KovaFlow_m8.rst" /> 3</FUNCTION>
Note the use of the F tag to indicate the use of a file. In contrast, the exact solution is
prescribed using analytic expressions which requires the use of the E tag.
1<FUNCTION NAME="ExactSolution"> 2 <E VAR="u" VALUE="1-exp(LAMBDA*x)*cos(2*PI*y)" /> 3 <E VAR="v" VALUE="(LAMBDA/2/PI)*exp(LAMBDA*x)*sin(2*PI*y)" /> 4 <E VAR="p" VALUE="0.5*(1-exp(2*LAMBDA*x))" /> 5</FUNCTION>
Launch the simulation using the following command
IncNavierStokesSolver KovaFlow_m8.xml
After completing the prescribed 100 time-steps, the difference between the computed solution and the exact solution will be displayed. The actual mantissas may vary slightly, but the overall magnitude should be as shown.
L 2 error (variable u) : 3.75296e-07 L inf error (variable u) : 5.13518e-07 L 2 error (variable v) : 1.68897e-06 L inf error (variable v) : 2.23918e-06 L 2 error (variable p) : 1.46078e-05 L inf error (variable p) : 5.18682e-05
The output of the simulation is written to KovaFlow_m8.fld. This can be visualised by
converting it to a visualisation format. For example, to use ParaView, convert the output into
VTK format using the tility.
FieldConvert KovaFlow.xml KovaFlow.fld KovaFlow.vtu
The result should look similar to that shown in Figure 11.6.
In this example, we solve the same case of 2D Kovasznay flow on severely-truncated computational domain but using a high-order outflow boundary condition, which is much more accurate and robust for unbounded flows [10]. The solver information and parameters used here are similar to the previous one. What only we need to modify in the input file is just the boundary condition type upon the outlet region shown as below
1<BOUNDARYCONDITIONS> 2 <REGION REF="0"> 3 <D VAR="u" VALUE="1-exp(KovLam*x)*cos(2*PI*y)" /> 4 <D VAR="v" VALUE="(KovLam/2/PI)*exp(KovLam*x)*sin(2*PI*y)" /> 5 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 6 </REGION> 7 <REGION REF="1"> 8 <N VAR="u" USERDEFINEDTYPE="HOutflow" 9 VALUE="-Kinvis*KovLam*exp(KovLam*x)*cos(2*PI*y) 10 - 0.5*(1-exp(2*KovLam*x))-0.5*(((1-exp(KovLam*x)*cos(2*PI*y)) 11 *(1-exp(KovLam*x)*cos(2*PI*y))+(KovLam/(2*PI)*exp(KovLam*x) 12 *sin(2*PI*y))*(KovLam/(2*PI)*exp(KovLam*x)*sin(2*PI*y)))) 13 *(0.5*(1.0-tanh((1-exp(KovLam*x)*cos(2*PI*y))*20)))" /> 14 <N VAR="v" USERDEFINEDTYPE="HOutflow" 15 VALUE="Kinvis*KovLam*KovLam/(2*PI)*exp(KovLam*x)*sin(2*PI*y)" /> 16 <D VAR="p" USERDEFINEDTYPE="HOutflow" 17 VALUE="-Kinvis*KovLam*exp(KovLam*x)*cos(2*PI*y) 18 - 0.5*(1-exp(2*KovLam*x)) -0.5*(((1-exp(KovLam*x)*cos(2*PI*y)) 19 *(1-exp(KovLam*x)*cos(2*PI*y))+(KovLam/(2*PI)*exp(KovLam*x) 20 *sin(2*PI*y))*(KovLam/(2*PI)*exp(KovLam*x)*sin(2*PI*y)))) 21 *(0.5*(1.0-tanh((1-exp(KovLam*x)*cos(2*PI*y))*20)))" /> 22 </REGION> 23 <REGION REF="2"> 24 <N VAR="u" VALUE="0" /> 25 <D VAR="v" VALUE="0" /> 26 <N VAR="p" VALUE="0" /> 27 </REGION> 28</BOUNDARYCONDITIONS>
We note that in this example the VALUE property is set based on the analytic solution but this
is not typically known and so often a VALUE of zero will be specified.
Instead of loading an initial condition from a specified file, we initialized the flow fields in this example by using following expressions
1<FUNCTION NAME="InitialConditions"> 2 <E VAR="u" VALUE="(1-exp(KovLam*x)*cos(2*PI*y))" /> 3 <E VAR="v" VALUE="(KovLam/(2*PI))*exp(KovLam*x)*sin(2*PI*y)" /> 4 <E VAR="p" VALUE="0.5*(1-exp(2*KovLam*x))" /> 5</FUNCTION>
We then launch the simulation by the same solver as that in the previous example
IncNavierStokesSolver KovaFlow_m8_short_HOBC.xml
The solution with errors displayed as below
L 2 error (variable u) : 2.51953e-08 L inf error (variable u) : 9.56014e-09 L 2 error (variable v) : 1.10694e-08 L inf error (variable v) : 9.47464e-08 L 2 error (variable p) : 5.59175e-08 L inf error (variable p) : 2.93085e-07
The physical solution visualized in velocity profiles is also illustrated in Figure 11.7.
In this example, we will simulate the flow through a channel at Reynolds number (Re) 1 with fixed boundary conditions.
The input file for this example is given in ChanFlow_m3_SKS.xml. The geometry is a square
channel with height and length D = 1, discretised using four quadrilateral elements. We use a
quadratic expansion order, which is sufficient to capture the quadratic flow profile. In this
example, we choose to use the skew-symmetric form of the advection term. This is chosen in
the solver information section:
1<I PROPERTY="EvolutionOperator" VALUE="SkewSymmetric" />
A first-order time integration scheme is used and we set the time-step and number of time integration steps in the parameters section. We also prescribe the kinematic viscosity ν = 1∕Re = 1.
Boundary conditions are defined on the walls (region 0) and at the inflow (regions 1) as Dirichlet for the velocity field and as high-order for the pressure. At the outflow the velocity is left free using Neumann boundary conditions and the pressure is pinned to zero.
1<BOUNDARYCONDITIONS> 2 <REGION REF="0"> 3 <D VAR="u" VALUE="0" /> 4 <D VAR="v" VALUE="0" /> 5 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 6 </REGION> 7 <REGION REF="1"> 8 <D VAR="u" VALUE="y*(1-y)" /> 9 <D VAR="v" VALUE="0" /> 10 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 11 </REGION> 12 <REGION REF="2"> 13 <N VAR="u" VALUE="0" /> 14 <N VAR="v" VALUE="0" /> 15 <D VAR="p" VALUE="0" /> 16 </REGION> 17</BOUNDARYCONDITIONS>
Initial conditions are set to zero. The exact solution is a parabolic profile with a pressure gradient dependent on the Reynolds number. This is defined to allow verification of the calculation.
1<FUNCTION NAME="ExactSolution"> 2 <E VAR="u" VALUE="y*(1-y)" /> 3 <E VAR="v" VALUE="0" /> 4 <E VAR="p" VALUE="-2*Kinvis*(x-1)" /> 5</FUNCTION>
IncNaverStokesSolver ChanFlow_m3_SKS.xml
The error in the solution should be displayed and be close to machine precision
L 2 error (variable u) : 4.75179e-16 L inf error (variable u) : 3.30291e-15 L 2 error (variable v) : 1.12523e-16 L inf error (variable v) : 3.32197e-16 L 2 error (variable p) : 1.12766e-14 L inf error (variable p) : 7.77156e-14
The solution should look similar to that shown in Figure 11.8.
We now solve the incompressible Navier-Stokes equations on a three-dimensional domain using all element types supported by Nektar++ which include Hexahedrons, Prisms, Pyramids and Tetrahedrons. In particular, we solve the three-dimensional equivalent of the previous example. We will also run the IncNavierStokesolver solver in parallel.
The input file for this example is given in the directory
$NEkHOME/solvers/IncNavierStokesolver/Examples/ChannelFlow3D.
In this example we use tetrahedral elements, indicated by the A element tags in the geometry
section. All dimensions have length D = 1. We will use a 7th-order polynomial expansion.
Since we now have three dimensions, and therefore three velocity components, the expansions
section is now
1<EXPANSIONS> 2 <E COMPOSITE="C[0]" NUMMODES="8" FIELDS="u,v,w,p" TYPE="MODIFIED" /> 3</EXPANSIONS>
The solver information and parameters are similar to the previous example. Boundary conditions must now be defined on the six faces of the domain. Flow is prescribed in the z-direction through imposing a Poiseulle profile on the inlet and side walls. The outlet is zero-Neumann and top and bottom faces impose zero-Dirichlet conditions.
1<BOUNDARYREGIONS> 2 <B ID="0"> C[1] </B> <!-- Inlet --> 3 <B ID="1"> C[6] </B> <!-- Outlet --> 4 <B ID="2"> C[2] </B> <!-- Wall --> 5 <B ID="3"> C[3] </B> <!-- Wall left --> 6 <B ID="4"> C[4] </B> <!-- Wall --> 7 <B ID="5"> C[5] </B> <!-- Wall right --> 8</BOUNDARYREGIONS> 9 10<BOUNDARYCONDITIONS> 11 <REGION REF="0"> 12 <D VAR="u" VALUE="0" /> 13 <D VAR="v" VALUE="0" /> 14 <D VAR="w" VALUE="y*(1-y)" /> 15 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 16 </REGION> 17 <REGION REF="1"> 18 <N VAR="u" VALUE="0" /> 19 <N VAR="v" VALUE="0" /> 20 <N VAR="w" VALUE="0" /> 21 <D VAR="p" VALUE="0" /> 22 </REGION> 23 <REGION REF="2"> 24 <D VAR="u" VALUE="0" /> 25 <D VAR="v" VALUE="0" /> 26 <D VAR="w" VALUE="0" /> 27 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 28 </REGION> 29 <REGION REF="3"> 30 <D VAR="u" VALUE="0" /> 31 <D VAR="v" VALUE="0" /> 32 <D VAR="w" VALUE="y*(1-y)" /> 33 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 34 </REGION> 35 <REGION REF="4"> 36 <D VAR="u" VALUE="0" /> 37 <D VAR="v" VALUE="0" /> 38 <D VAR="w" VALUE="0" /> 39 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 40 </REGION> 41 <REGION REF="5"> 42 <D VAR="u" VALUE="0" /> 43 <D VAR="v" VALUE="0" /> 44 <D VAR="w" VALUE="y*(1-y)" /> 45 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 46 </REGION> 47</BOUNDARYCONDITIONS>
Initial conditions and exact solutions are also prescribed.
To run the solver in parallel, we use the mpirun command.
mpirun -np 2 IncNaverStokesSolver ChannelFlow3D.xml
The expected results are shown in Figure 11.9.
For domains where at least one direction is geometrically homogeneous, a more efficient discretisation is to use a pure spectral discretisation, such as a Fourier expansion, in these directions. We use this approach to solve the same problem as in the previous example. We reuse the two-dimensional spectral/hp element mesh from the nd couple this with a Fourier expansion in the third component.
The input file for this example is ChanFlow_3DH1D_MVM.xml. We indicate that we are coupling
the spectral/hp element domain with a pure spectral expansion using the following solver
information
1<I PROPERTY="HOMOGENEOUS" VALUE="1D"/>
We must also specify parameters to describe the particular spectral expansion
1<P> HomModesZ = 20 </P> 2<P> LZ = 1.0 </P>
The parameter HomModesZ specifies the number of Fourier modes to use in the homogeneous
direction. The LZ parameter specifies the physical length of the domain in that
direction.
As with the the spectral/hp element mesh consists of four quadrilateral elements with a second-order polynomial expansion. Since our domain is three-dimensional we have to now include the third velocity component
1<E COMPOSITE="C[0]" NUMMODES="3" FIELDS="u,v,w,p" TYPE="MODIFIED" />
The remaining parameters and solver information is similar to previous examples.
Boundary conditions are specified as for the two-dimensional case (except with the addition of the third velocity component) since the side walls are now implicitly periodic. The initial conditions and exact solution are prescribed as for the fully three-dimensional case.
IncNaverStokesSolver ChannelFlowQuasi3D.xml
The results can be post-processed and should match those of the fully three-dimensional case as shown in Figure 11.9.
In this example, we illustrate how to perform a biglobal or direct stability analysis using Nektar++ which determines the leading eigenvalues and eigenvectors of the the linearised Navier-Stokes equations:
In this appraoch we use a time stepping approached as part of an Arnoldi iterative scheme [7].
We consider a canonical stability problem, the flow in a channel which is confined in the wall-normal direction between two infinite plates (Poiseuille flow) at Reynolds number (Re) 7500. This problem is a particular case of the stability solver for the IncNavierStokesSolver.
An example input files can be found under:
$NEkHOME/solvers/IncNavierStokesolver/Examples/ChannelStability.
In this directory there are three files: the session and geometry file ChannelStability.xml, a
base flow file ChannelStbaility.bse and a restart file ChannelStability.rst.
In this example the EvolutionOperator must be Direct to consider the linearised
Navier-Stokes equations and the Driver is set up to ModifiedArnoldi for the solution of the
eigenproblem.
1 <SOLVERINFO> 2 <I PROPERTY="SolverType" VALUE="VelocityCorrectionScheme" /> 3 <I PROPERTY="EQTYPE" VALUE="UnsteadyNavierStokes" /> 4 <I PROPERTY="EvolutionOperator" VALUE="Direct" /> 5 <I PROPERTY="Projection" VALUE="Galerkin" /> 6 <I PROPERTY="Driver" VALUE="ModifiedArnoldi" /> 7 </SOLVERINFO>
For a stability run we require the following parameters
1<PARAMETERS> 2 <P> TimeStep = 0.002 </P> 3 <P> NumSteps = 500 </P> 4 <P> IO_CheckSteps = 1000 </P> 5 <P> IO_InfoSteps = 10 </P> 6 <P> Re = 7500 </P> 7 <P> Kinvis =1./Re </P> 8 <P> kdim =16 </P> 9 <P> nvec =2 </P> 10 <P> evtol =1e-5</P> 11 <P> nits =5000 </P> 12 </PARAMETERS>
Here the TimeStep and NumSteps define for how long we run the time stepping scheme to
perform a forward/direct action of the linearised Navier-Stokes equation over a
fixed time TimeStep x NumSteps. As previously we set the Reynolds number based
on the kinematic viscosity, inflow velocity and channel height (the latter two are
assumed to be one). The Arnoldi parameters are provide by kdim which defines
the dimension of the Krylov space, nvec which defines the number of eigenvalues
to converge to tolerance evtol and nits gives the maximum number of Arnoldi
iterations.
Similar to the Navier-Stokes equations we specify similar boundary conditions where typically the linearised problem is zero on most boundaries.
1 <BOUNDARYREGIONS> 2 <B ID="0"> C[1] </B> 3 <B ID="1"> C[2] </B> 4 <B ID="2"> C[3] </B> 5 </BOUNDARYREGIONS> 6 7 <BOUNDARYCONDITIONS> 8 <REGION REF="0"> 9 <D VAR="u" VALUE="0" /> 10 <D VAR="v" VALUE="0" /> 11 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 12 </REGION> 13 <REGION REF="1"> 14 <P VAR="u" VALUE="[2]" /> 15 <P VAR="v" VALUE="[2]" /> 16 <P VAR="p" VALUE="[2]" /> 17 </REGION> 18 <REGION REF="2"> 19 <P VAR="u" VALUE="[1]" /> 20 <P VAR="v" VALUE="[1]" /> 21 <P VAR="p" VALUE="[1]" /> 22 </REGION> 23 </BOUNDARYCONDITIONS> 24
For the linearised problem we need to set up the base flow that can be specified as a function
BaseFlow. In case the base flow is not analytical, it can be generated by means of the
Nonlinear evolution operator using the same mesh and polynomial expansion. The initial
guess is specified in the InitialConditions functions and can be both analytical or a file. In
this example it is read from a file.
1 <FUNCTION NAME="BaseFlow"> 2 <F VAR="u,v,p" FILE="ChannelStability.bse" /> 3 </FUNCTION> 4
As in previous examples we also can specify a restart file using the InitialConditions
section
1 <FUNCTION NAME="InitialConditions"> 2 <F VAR="u,v,p" FILE="ChannelStability.rst" /> 3 </FUNCTION> 4
As previously once we have set up the xml file appropriatel we can simply run:
IncNavierStokesSolver ChannelStability.xml
The stability simulation takes about 250 iterations to converge and the dominant eigenvalues (together with the respective eigenvectors) will be visualised. In this case the files are given as
ChannelStability_eig_0.xml and ChannelStability_eig_1.xml
which can be post processed using FieldConvert.
The eigenvalues are provided in the file ChannelStability.evl and in this case it was found
λ1,2 = 1.000224 ×e±0.24984i. Therefore, since the magnitude of the eigenvalue is larger than 1,
the flow is absolutely unstable. It is possible to visualise the eigenvectors using the
post-processing utilities. The figure shows the profile of the two eigenmode component,
which shows the typical Tollmien - Schlichting waves that arise in viscous boundary
layers.
We consider in this example how to perform an adjoint stability analysis using Nektar++. We consider a canonical stability problem, the flow in a channel which is confined in the wall-normal direction between two infinite plates (Poiseuille flow) at Reynolds number (Re) 7500
The adjoint equations of the linearised Navier-Stokes equations can be written as
We are interested in computing the leading eigenvalue of the system using the Arnoldi method [7].
An example input files can be found under:
$NEkHOME/solvers/IncNavierStokesolver/Examples/ChannelStabilityAdjoint.
In this directory there are three files: the session and geometry file ChannelStabilityAdjoint.xml,
a base flow file ChannelStbailityAdjoint.bse and a restart file ChannelStabilityAdjoint.rst.
In this example the EvolutionOperator must be set to Adjoint to consider the adjoint
Navier-Stokes equations defined above and the Driver was set up to ModifiedArnoldi for the
solution of the eigenproblem, i.e.
1<SOLVERINFO> 2 <I PROPERTY="SolverType" VALUE="VelocityCorrectionScheme" /> 3 <I PROPERTY="EQTYPE" VALUE="UnsteadyNavierStokes" /> 4 <I PROPERTY="EvolutionOperator" VALUE="Adjoint" /> 5 <I PROPERTY="Projection" VALUE="Galerkin" /> 6 <I PROPERTY="Driver" VALUE= "ModifiedArnoldi" /> 7</SOLVERINFO> 8 \end{subequations} 9 10\subsubsection*{Parameters} 11 12Similar to the BiGlobal problem we specify the parameters: 13 14\begin{lstlisting}[style=XMLStyle] 15<PARAMETERS> 16 <P> TimeStep = 0.002 </P> 17 <P> NumSteps = 500 </P> 18 <P> IO_CheckSteps = 1000 </P> 19 <P> IO_InfoSteps = 10 </P> 20 <P> Re = 7500 </P> 21 <P> Kinvis =1./Re </P> 22 <P> kdim =16 </P> 23 <P> nvec =2 </P> 24 <P> evtol =1e-5</P> 25 <P> nits =5000 </P> 26</PARAMETERS> 27
Here the TimeStep and NumSteps define for how long we run the time stepping scheme to the
adjoint of the linearised Navier-Stokes equation over a fixed time TimeStep x NumSteps. We
set the Reynolds number based on the kinematic viscosity, inflow velocity and channel height
(the latter two are assumed to be one). The Arnoldi parameters are provide by kdim which
defines the dimension of the Krylov space, nvec which defines the number of eigenvalues
to converge to tolerance evtol and nits gives the maximum number of Arnoldi
iterations.
In this case we have a periodic domain and so we only have to worry about the adjoint variables on the walls which are set to zero.
1 <BOUNDARYREGIONS> 2 <B ID="0"> C[1] </B> 3 <B ID="1"> C[2] </B> 4 <B ID="2"> C[3] </B> 5 </BOUNDARYREGIONS> 6 7 <BOUNDARYCONDITIONS> 8 <REGION REF="0"> 9 <D VAR="u" VALUE="0" /> 10 <D VAR="v" VALUE="0" /> 11 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 12 </REGION> 13 <REGION REF="1"> 14 <P VAR="u" VALUE="[2]" /> 15 <P VAR="v" VALUE="[2]" /> 16 <P VAR="p" VALUE="[2]" /> 17 </REGION> 18 <REGION REF="2"> 19 <P VAR="u" VALUE="[1]" /> 20 <P VAR="v" VALUE="[1]" /> 21 <P VAR="p" VALUE="[1]" /> 22 </REGION> 23 </BOUNDARYCONDITIONS> 24
We need to set up the base flow that can be specified as a function BaseFlow. In case the base
flow is not analytical, it can be generated by means of the Nonlinear evolution operator using
the same mesh and polynomial expansion.
1 <FUNCTION NAME="BaseFlow"> 2 <F VAR="u,v,p" FILE="ChanStabilityAdjoint.bse" /> 3 </FUNCTION> 4
The initial guess is specified in the InitialConditions functions and can be both analytical
or a file. In this example it is read from a file.
1 <FUNCTION NAME="InitialConditions"> 2 <F VAR="u,v,p" FILE="ChanStabilityAdjoint.rst" /> 3 </FUNCTION> 4
Execution is relatively straightforward once the input files are setup:
IncNavierStokesSolver ChannelStabilityAdjoint.xml
The equations will then be evolved backwards in time (consistently with the negative sign in
front of the time derivative) and the leading eigenvalues will be computed after about 300
iterations. It is interesting to note that their value is the same one computed for the direct
problem, but the eigenmodes present a different shape. As in the biglobal stability problem
the adjoint eigenvalues are given in the file ChannelStabilityAjoint.evl and
the eigenvectors are provided in file ChannelStabilityAdjoint_eig_0.fld and
ChannelStabilityAdjoint_eig_1.fld
In this example we consider how to perform a transient growth stability analysis using Nektar++. Let us consider a flow past a backward-facing step (figure 11.14). This is an important case because it allows us to understand the effects of separation caused by abrupt changes in the geometry and it is a common geometry in several studies of flow control and turbulence of separated flow.
Transient growth analysis allows us to study the presence of convective instabilities that can arise in stable flows. Despite the fact that these instabilities will decay for a long time (due to the stability of the flow), they can produce significant increases in the energy of perturbations. The phenomenon of transient growth is associated with the non-normality of the linearised Navier-Stokes equations and it consists in computing the perturbation that leads to the highest energy growth for a fixed time horizon [7].
An example input files can be found under:
$NEkHOME/solvers/IncNavierStokesolver/Examples/BackwardFacingStep_TG.
In this directory there are three files: the session and geometry file BackwardsFacingStep_TG.xml,
a base flow file BackwardsFacingStep_TG.bse and a restart file BackwardsFacingStep_TG.rst.
In this example the EvolutionOperator must be TransientGrowth and the Driver was set
up to Arpack for the solution of the eigenproblem. This means the code msut be compiled wit
the option NEKTAR_USE_ARPACK turned on. For this example the solver parameters
are:
1<SOLVERINFO> 2 <I PROPERTY="EQTYPE" VALUE="UnsteadyNavierStokes" /> 3 <I PROPERTY="EvolutionOperator" VALUE="TransientGrowth" /> 4 <I PROPERTY="Projection" VALUE="Galerkin" /> 5 <I PROPERTY="SOLVERTYPE" VALUE="VelocityCorrectionScheme" /> 6 <I PROPERTY="Driver" VALUE="Arpack" /> 7 <I PROPERTY="ArpackProblemType" VALUE="LargestMag" /> 8</SOLVERINFO> 9
1<PARAMETERS> 2 <P> FinalTime = 0.1 </P> 3 <P> TimeStep = 0.005 </P> 4 <P> NumSteps = FinalTime/TimeStep </P> 5 <P> IO_CheckSteps = 1/TimeStep </P> 6 <P> IO_InfoSteps = 1 </P> 7 <P> Re = 500 </P> 8 <P> Kinvis = 1.0/Re </P> 9 <P> kdim = 4 </P> 10 <P> nvec = 1 </P> 11 <P> evtol = 1e-4 </P> 12</PARAMETERS> 13
Here the FinalTime to define for how long we run the time stepping scheme to perform a
forward/direct and backwards action of the linearised and adjoint Navier-Stokes equation over
a fixed time TimeStep x NumSteps. As previously we set the Reynolds number based on the
kinematic viscosity, inflow velocity and step height (the latter two are assumed to be one).
The Arnoldi parameters are provide by kdim which defines the dimension of the
Krylov space, nvec which defines the number of eigenvalues to converge to tolerance
evtol.
To satisy the boundary coditiosn for both the forward linearised and the backwards adjoint problems we set the otuflow and inflow conditiosn to zero Dirichlet. Similarly on the walls we have zeor Dirichlet conditions.
1 <BOUNDARYREGIONS> 2 <B ID="0"> C[2] </B> <!-- Wall --> 3 <B ID="1"> C[3] </B> <!-- Inlet --> 4 <B ID="2"> C[4] </B> <!-- Outlet --> 5 </BOUNDARYREGIONS> 6 7 <BOUNDARYCONDITIONS> 8 <REGION REF="0"> 9 <D VAR="u" VALUE="0" /> 10 <D VAR="v" VALUE="0" /> 11 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 12 </REGION> 13 <REGION REF="1"> 14 <D VAR="u" VALUE="0" /> 15 <D VAR="v" VALUE="0" /> 16 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 17 </REGION> 18 <REGION REF="2"> 19 <D VAR="u" VALUE="0" /> 20 <D VAR="v" VALUE="0" /> 21 <N VAR="p" USERDEFINEDTYPE="H" VALUE="0" /> 22 </REGION> 23 </BOUNDARYCONDITIONS> 24
We need to set up the base flow that can be specified as a function BaseFlow. In case the base
flow is not analytical, it can be generated by means of the Nonlinear evolution operator using
the same mesh and polynomial expansion.
1<FUNCTION NAME="BaseFlow"> 2 <F VAR="u,v,p" FILE="BackwardsFacingStep_TG.bse" /> 3 </FUNCTION> 4
An initial guess can be specified in the InitialConditions functions and in this case is read
from a file.
1<FUNCTION NAME="InitialConditions"> 2 <F VAR="u,v,p" FILE="BackwardsFacingStep_TG.rst" /> 3/FUNCTION> 4
Execution is relatively straightforward once the input files are setup:
IncNavierStokesSolver BackwardsFacingdtep_TG.xml
The solution will be evolved forward in time using the operator A, then backward in time through the adjoint operator A*. The leading eigenvalue is λ = 3.236204). This corresponds to the largest possible transient growth at the time horizon τ = 1. The leading eigenmode is shown below. This is the optimal initial condition which will lead to the greatest growth when evolved under the linearised Navier-Stokes equations.
It is possible to visualise the transient growth plotting the energy evolution over time if the system is initially perturbed with the leading eigenvector. This analysis was performed for a time horizon τ = 60. It can be seen that the energy grows in time reaching its maximum value at x = 24 and then decays, almost disappearing after 100 temporal units.