6.4 Examples

6.4.1 Wave Propagation in a Sheared Base Flow

In this section we explain how to set up a simple, 2D simulation of aeroacoustics in Nektar++. We will study the propagation of an acoustic wave in the simple case of a sheared base flow, i.e. u = ^T, c² = ², ρ = 1.204kg∕m³. The geometry consists of 64 quadrilateral elements.

6.4.1.1 Input file

We require a discontinuous Galerkin projection and use an explicit fourth-order Runge-Kutta time integration scheme. We therefore set the following time integration schem and solver information:

1<TIMEINTEGRATIONSCHEME> 
2    <METHOD> RungeKutta </METHOD> 
3    <ORDER> 4 </ORDER> 
4</TIMEINTEGRATIONSCHEME> 
5 
6<SOLVERINFO> 
7    <I PROPERTY="EQType"                VALUE="APE"/> 
8    <I PROPERTY="Projection"            VALUE="DisContinuous"/> 
9    <I PROPERTY="UpwindType"            VALUE="LaxFriedrichs"/> 
10</SOLVERINFO>

To maintain numerical stability we must use a small time-step. Finally, we set the density, heat ratio and ambient pressure.

1<PARAMETERS> 
2    <P> TimeStep       = 1e-05              </P> 
3    <P> NumSteps       = 1000               </P> 
4    <P> FinTime        = TimeStep*NumSteps  </P> 
5    <P> IO_CheckSteps  = 10                 </P> 
6    <P> IO_InfoSteps   = 10                 </P> 
7</PARAMETERS>

The initial condition and the base flow field are specified by the Baseflow and InitialConditions functions, respectively:

1<FUNCTION NAME="Baseflow"> 
2  <E VAR="u0" VALUE="300 * tanh(2*y/0.1)"/> 
3  <E VAR="v0" VALUE="0"/> 
4  <E VAR="c0sq" VALUE="1.4 * Pinfinity / Rho0"/> 
5  <E VAR="rho0" VALUE="Rho0"/> 
6</FUNCTION> 
7<FUNCTION NAME="InitialConditions"> 
8  <E VAR="p" VALUE="0"/> 
9  <E VAR="u" VALUE="0"/> 
10  <E VAR="v" VALUE="0"/> 
11</FUNCTION>

At all four boundaries the RiemannInvariantBC condition is used:

1<BOUNDARYCONDITIONS> 
2  <REGION REF="0"> 
3    <D VAR="p" USERDEFINEDTYPE="RiemannInvariantBC"/> 
4    <D VAR="u" USERDEFINEDTYPE="RiemannInvariantBC"/> 
5    <D VAR="v" USERDEFINEDTYPE="RiemannInvariantBC"/> 
6  </REGION> 
7</BOUNDARYCONDITIONS>

The system is excited via an acoustic source term _c, which is modeled by a field forcing as:

1<FORCING> 
2  <FORCE TYPE="Field"> 
3    <FIELDFORCE> Source <FIELDFORCE/> 
4  </FORCE> 
5</FORCING>

and the corresponding function

1<FUNCTION NAME="Source"> 
2  <E VAR="p" VALUE="100 * 2*PI*5E2 * cos(2*PI*5E2 * t) * exp(-32*(x^2+y^2))"/> 
3  <E VAR="u" VALUE="0"/> 
4  <E VAR="v" VALUE="0"/> 
5</FUNCTION>

6.4.1.2 Running the code

AcousticSolver Test_pulse.xml

6.4.1.3 Results

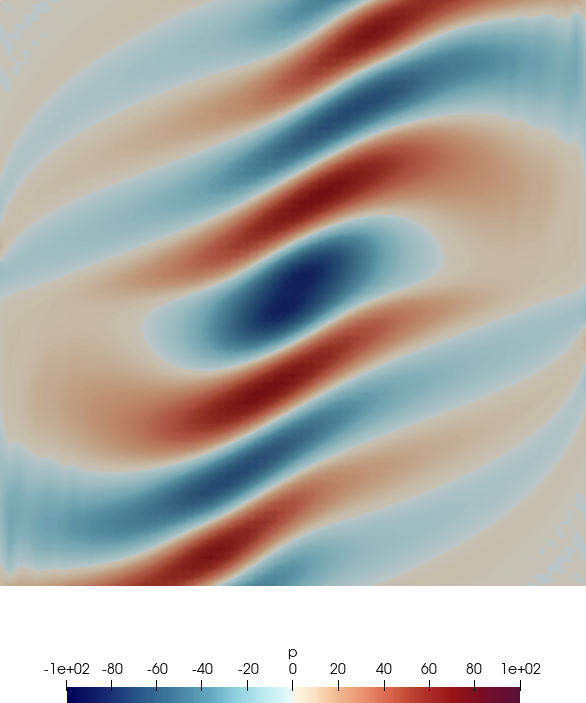
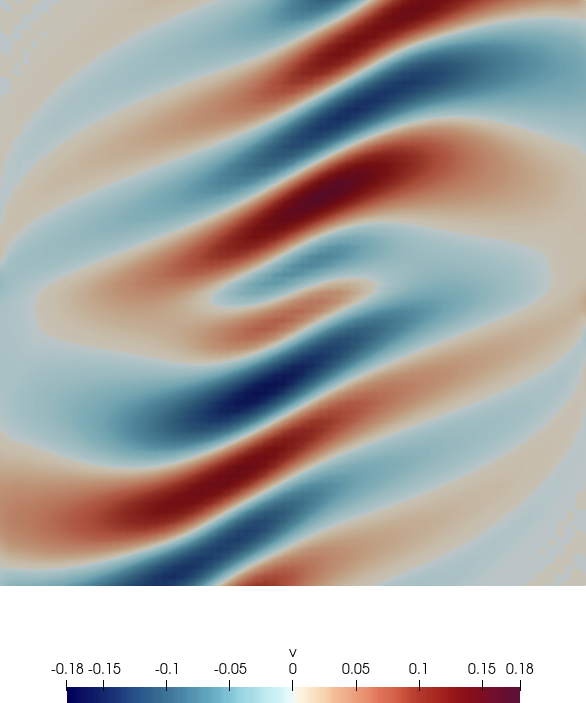
Fig. 6.1 shows the acoustic source term, the velocity and the acoustic pressure and velocity perturbations at a single time step.