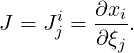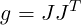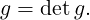6.1 The Fundamentals Behind SpatialDomains
As mentioned in our discussions of the fundamentals of StdRegions (i.e. Section 5.1), one of
the most fundamental tools from calculus that we regularly employ is the idea of mapping
from general domains to canonical domains. General domains are the regions in
world space over which we want to solve engineering problems, and thus want to be
able to take derivatives and compute integrals. But as we learned in calculus, it is
often non-trivial to accomplish differentiation or integration over these regions. We
resort to the mapping arbitrary domains back to canonical domains over which
we can define various operations. We introduced our canonical domains, which we
call standard regions, in Chapter 5. We refer to our world space regions as local
regions, which we will present in Chapter 7. How these two are connected are via
SpatialDomains.
As will be further discussed in Section 6.2, there are two fundamental purposes served by
SpatialDomains: (1) holding basic geometric information (e.g. vertex values and
curvature information) and (2) holding geometric factors information. The former
information relates to the geometric way we map standard regions to local regions.
The latter information relates to how we use this map to allow us to accomplish
differentiation and integration of functions in world space via operations on standard regions
with associated map (geometric) information. In this section, we will highlight the
important mathematical principles that are relevant to this section. We will first discuss
the mapping itself: vertex and curvature information and how it is used. We will
then discuss how geometric factor information is computed. We break this down
into two subsections following the convention of the code. We will first discussed
what is labeled in the code as Regular, and denotes mappings between elements of
the same dimension (i.e. standard region triangles to 2D triangles in world space).
Although our notation will be slightly different, we will use [46] as our guide; we refer
the interested reader there for a more in-depth discussion of these topics. We will
then discuss what is labeled in the code as Deformed, and denotes the mappings
between standard region elements and their world space variants in a higher embedded
dimension (i.e. standard region triangles to triangles lying on a surface embedded in
a 3D space representing a manifold). Since the manifold work within Nektar++
was introduced as an area of research, we will use [18] as our guide. The notation
therein is slightly different than that of [46] because of the necessity to use broader
coordinate system transformation principles (e.g. covariance and contravariance of
vectors, etc.). We will abbreviate the detailed mathematical derivations here, but
encourage the interested reader to review [18] and references therein as needed. For those
unfamiliar with covariant and contravariant spaces, we encourage the reader to review
[13].
6.1.1 Vertex and Curvature Mapping Information
When we load in a mesh into Nektar++, elements are often described in world space based
upon their vertex positions. In traditional FEM formats, this can be as simple as a list of
d-dimensional vertex coordinates, followed by a list of element definitions: each row holding
four integers (in the case of tetrahedra) denoting the four vertices in the vertex
list that comprise an element. Nektar++ uses an HTML-based geometry file with
a more rich definition of the basic geometric information that just described; we
encourage developers and users to review our User Guide(s) for the organization and
conventions used within our geometry files. For the purposes of this section, the
important pieces of information are as follows. Let us assume that for each element,
we have through our MeshGraph data structure (described in the next section)
access to the vertex positions of an element. In general, each vertex 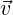 j is a n-tuple
of dimension d denoting the dimension in which the points are specified in world
space. For example, when considering a quadrilateral on the 2D plane, our vertex
points each contain two coordinates denotes the x– and y–coordinates. As shown in
Figure 6.1, we can express the mapping between a world space quadrilateral and the
standard region quadrilateral on [-1,1] × [-1,1] via a bi-linear mapping function
χ(
j is a n-tuple
of dimension d denoting the dimension in which the points are specified in world
space. For example, when considering a quadrilateral on the 2D plane, our vertex
points each contain two coordinates denotes the x– and y–coordinates. As shown in
Figure 6.1, we can express the mapping between a world space quadrilateral and the
standard region quadrilateral on [-1,1] × [-1,1] via a bi-linear mapping function
χ(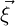 ).
).
In the case of segments, this mapping function χ(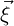 ) is a function of one variable and is merely
an affine mapping. In two dimensions, the mapping of a straight-sided triangle is a linear
mapping (i.e., P(1) in the language of traditional finite elements – a total degree k = 1
space) and the mapping of a straight-sided quadrilateral is a bi-linear mapping (i.e,
Q(1) in the language of traditional finite elements – a degree k = 1 map along each
coordinate direction combined through tensor-product). In three dimensions, the
mapping of a planar-sided tetrahedron is also a linear mapping, the mapping of a
planar-sided hexahedron is a tri-linear mapping, and the prism and pyramid are
mathematically somewhere in-between these two canonical types as given in [46]. The key
point is that in the case of straight-sided (or planar-sided) elements, the mapping
between reference space and world space can be deduced solely based upon the vertex
positions. Furthermore in these cases, as denoted in Figure 6.1, the form of the mapping
function is solely determined by type (shape) of the element. If only planar-sided
elements are used, pre-computation involving the mapping functions can be done
so that when vertex value information is available, all the data structures can be
finalized.
) is a function of one variable and is merely
an affine mapping. In two dimensions, the mapping of a straight-sided triangle is a linear
mapping (i.e., P(1) in the language of traditional finite elements – a total degree k = 1
space) and the mapping of a straight-sided quadrilateral is a bi-linear mapping (i.e,
Q(1) in the language of traditional finite elements – a degree k = 1 map along each
coordinate direction combined through tensor-product). In three dimensions, the
mapping of a planar-sided tetrahedron is also a linear mapping, the mapping of a
planar-sided hexahedron is a tri-linear mapping, and the prism and pyramid are
mathematically somewhere in-between these two canonical types as given in [46]. The key
point is that in the case of straight-sided (or planar-sided) elements, the mapping
between reference space and world space can be deduced solely based upon the vertex
positions. Furthermore in these cases, as denoted in Figure 6.1, the form of the mapping
function is solely determined by type (shape) of the element. If only planar-sided
elements are used, pre-computation involving the mapping functions can be done
so that when vertex value information is available, all the data structures can be
finalized.
As presented in ??, there are many components of Nektar++ that capitalize on the geometric
nature of the basis functions we use. We often speak in terms of vertex modes, edge modes,
face modes and internal modes – i.e., the coefficients that provide the weighting of vertex basis
functions, edge basis functions, etc. It is beyond the scope of this developer guide to go
into all the mathematical details of their definitions, etc. However, we do want to
point out a few common developer-level features that are important. In the case of
straight-sided (planar-sided) elements, the aforementioned mapping functions can be fully
described by vertex basis functions. The real benefit of this approach (of connecting
the mapping representation with a geometric basis) is seen when moving to curved
elements.
Consider Figure 6.2 in which we modify the example given above to accommodate on curved
edge. From the mathematical perspective, we know that the inclusion of this (quadratic) edge
will require our mapping function to now be in Q(2). If we were not to use the fact that our
basis is geometric in nature, we would be forced to form a Vandermonde system for a set of
coefficients used to combine the tensor-product quadratic functions (nine basis functions in
all), and use the five pieces of information available to us (the four vertex values and the one
point 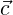 0 that informs the curve on edge 1. As shown in Figure 6.2, we would expect that this
updated (to accommodate a curved edge) mapping function to consist of the bi-linear mapping
function with an additional term C1(ξ1,ξ2) that encompasses the new curvature
information.
0 that informs the curve on edge 1. As shown in Figure 6.2, we would expect that this
updated (to accommodate a curved edge) mapping function to consist of the bi-linear mapping
function with an additional term C1(ξ1,ξ2) that encompasses the new curvature
information.
The basis we use, following [46], allows us to precisely specify C1(ξ1,ξ2) using the edge basis
function associated with edge 1, and to use the point value  0 to specify the coefficient to be
used. In the figure, we assume that the form of the function is collocating, but in practice it
need not be so.
0 to specify the coefficient to be
used. In the figure, we assume that the form of the function is collocating, but in practice it
need not be so.
In practice, edge (and face) information can be given either as a set of point positions in world
space that correspond to a particular point distribution in the reference element (i.e.,
evenly-spaced points or GLL points) or modal information corresponding to the geometric
basis we use internally. Our geometric file formats assume the former – that curve
information is provided to us as physical values at specified positions from which we
infer (calculate) the modal values and store these values within SpatialDomain data
structures.
Assuming we now have, for each element, a way of specifying the mapping function χ(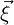 ), we
can now move to how we compute the geometric factors for regular as well as for deformed
mappings. We use the term “regular mappings" to refer to mappings from reference space
elements to world space elements with the same dimension. For instance, a collection of
triangles that lie in a plane can be represented by vertex coordinates that an only 2-tuples and
the mappings between the reference space triangle the and world space triangle does not need
to consider a larger embedded dimension. This was a fundamental assumption of the original
Nektar code: segments lived on the 1D line, triangles and quadrilaterals lived on the 2D plane
and that hexahedra, tetrahedra, etc., lived in the 3D volume. When redesigning
Nektar++, we purposefully enabled geometric entities to live in a high-dimensional
embedding space, different from their parameterized dimension. For instance, in
Nektar++, it is possible to define segment expansions (functions that live over one
dimensional parameterized curves) that are embedded in 3D. The same is true for
quadrilaterals and triangles – although their parameterized dimension is two, both
may live in a higher dimensional embedding space and thus represent a manifold of
co-dimension one in that space. For mappings that maintain the co-dimension is
the opposite of the dimension (i.e., quadrilateral in a plane represented by vertices
with two coordinates mapped to a two parameter reference quadrilateral), we keep
to the mapping conventions originally outlined in [46] and denote these mapping
operations in the code by the enumerated value Regular; for mappings in which the
co-dimension is greater than zero, we following the modified convention outlined in
[18] and denote these mapping operations in the code by the enumerated value
Deformed.
), we
can now move to how we compute the geometric factors for regular as well as for deformed
mappings. We use the term “regular mappings" to refer to mappings from reference space
elements to world space elements with the same dimension. For instance, a collection of
triangles that lie in a plane can be represented by vertex coordinates that an only 2-tuples and
the mappings between the reference space triangle the and world space triangle does not need
to consider a larger embedded dimension. This was a fundamental assumption of the original
Nektar code: segments lived on the 1D line, triangles and quadrilaterals lived on the 2D plane
and that hexahedra, tetrahedra, etc., lived in the 3D volume. When redesigning
Nektar++, we purposefully enabled geometric entities to live in a high-dimensional
embedding space, different from their parameterized dimension. For instance, in
Nektar++, it is possible to define segment expansions (functions that live over one
dimensional parameterized curves) that are embedded in 3D. The same is true for
quadrilaterals and triangles – although their parameterized dimension is two, both
may live in a higher dimensional embedding space and thus represent a manifold of
co-dimension one in that space. For mappings that maintain the co-dimension is
the opposite of the dimension (i.e., quadrilateral in a plane represented by vertices
with two coordinates mapped to a two parameter reference quadrilateral), we keep
to the mapping conventions originally outlined in [46] and denote these mapping
operations in the code by the enumerated value Regular; for mappings in which the
co-dimension is greater than zero, we following the modified convention outlined in
[18] and denote these mapping operations in the code by the enumerated value
Deformed.
6.1.2 Regular Mappings: Geometric Factors
Following [46], we assume that the vertex positions of an element in world space are given by
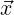 = xi and that our reference space coordinates are given by
= xi and that our reference space coordinates are given by 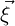 = ξj, there i and j run from
zero to dim - 1 where dim is the parameter dimension of the element (e.g. for a triangle,
dim = 2).
= ξj, there i and j run from
zero to dim - 1 where dim is the parameter dimension of the element (e.g. for a triangle,
dim = 2).
The Jacobian (matrix) is correspondingly defined as:
Note that this matrix is always square, but also note that it is not always constant across an
element. Only in special cases such as the linear mapping of triangles and tetrahedra
does the Jacobian matrix reduce to a constant (matrix) over the entire element. In
general, this matrix can be evaluated at any point over the element for which it is
constructed.
There are two (high-level) times in which this information is needed: when computing
derivatives and when computing integrals. When computing derivatives, we employ the
chain rule for differentiation, which in Einstein notation is given by the following
expression:
Note that this expression requires the reciprocal of the expression above – that is, J-1. The
polynomial mappings we use in Nektar++ are defined in terms of their forward mappings
(reference to world). If the determinant of the mapping is non-zero, the inverse of the mapping
exists but is not available analytically (except is special cases). As a consequence,
we in general limit the places at which we compute the inverse of the Jacobian.
Typically, the quadrature point positions are the places at which you need these
values (since it as at these points we take physical space derivates and then use
integration rules to construct weak form operators). Thus, procedurally, we do the
following:
- For a given element, compute the Jacobian matrix using the expression given in
Equation 6.2 for each quadrature point position on the element (or for any points
positions within an element at which it is needed).
- Explicitly form the inverse of the matrix at each point position.
Because we accomplish the inversion of the Jacobian matrix at particular positions, this
introduces an approximation to this computation. Although the inverse Jacobian matrix can
be computed exactly at each point – when we then correspondingly use this information in the
inner product over an element – we are in effect assuming that we are using a polynomial
interpolative projection of this operator. The approximation error is introduced at the point of
our quadrature approximation. Although the forward mapping is polynomial and hence we
could find a polynomial integration rule and number of points/weights to integrate our bilinear
forms exactly, our use of the inverse mapping in our bilinear forms means that we can only
approximate our integrals. From our experiments, the impact of his is negligible in
most cases, and only becomes in a concern in highly curved geometries. In such
cases, over-integration might be requires to minimize the errors introduced due this
approximation.
The other place at which we need the Jacobian matrix is to compute its determinant to
be used in integration. The determinant of the Jacobian matrix (sometimes also
called “the Jacobian" of the mapping) provides us the scaling of the metric terms
used in integration. In all our computations, we assume that the determinant of the
Jacobian matrix is strictly positive. In the area of mesh generation, the value of the
determinant is used to estimate how good or bad the quality of the mapping is – in
effect, if you have reasonable elements in your mesh. Negative Jacobian elements
are inadmissible but even elements with small Jacobian determinants might cause
issues. At the level of the library and solvers, we assume that these issues have been
addressed by the user prior to attempting to run Nektar++ solvers and interpret their
results.
6.1.3 Deformed Mappings: Geometric Factors
Following [18], we again assume that the vertex positions of an element in world space are
given by 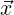 = xi and that our reference space coordinates are given by
= xi and that our reference space coordinates are given by 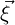 = ξj, there
i runs from zero to dim - 1 where dim is the embedding dimension and j runs
from zero to M - 1 where M is the parameter dimension of the element (e.g.for a
triangle on a manifold embedded in 3D with vertex values in 3D, dim = 3 whilst
M = 2).
= ξj, there
i runs from zero to dim - 1 where dim is the embedding dimension and j runs
from zero to M - 1 where M is the parameter dimension of the element (e.g.for a
triangle on a manifold embedded in 3D with vertex values in 3D, dim = 3 whilst
M = 2).
The Jacobian (matrix) is correspondingly defined as:
In this case, we use the notational conventions of [8] which delineate covariant and
contravariant forms. In general, this matrix is not square, also also note that it is not always
constant across an element. In general, this matrix can be evaluated at any point over the
element for which it is constructed. The metric tensor related to this transformation can be
formed as:
and the Jacobian factor associated with this mapping is then given by:
Because various mappings are necessary when dealing with covariant and contravariant
vectors, we have encapsulated all these routines into the directory GlobalMapping (see
Chapter 10). At this stage, we do not implement general Piola transformations [54] that
further respect H(div) and H(curl) constraints on these mappings as would be needed in solid
mechanics or electromagnetics; however, there is nothing inherent within the Nektar++
framework that would preclude someone from adding these additional features as
necessary.
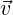 j is a n-tuple
of dimension d denoting the dimension in which the points are specified in world
space. For example, when considering a quadrilateral on the 2D plane, our vertex
points each contain two coordinates denotes the x– and y–coordinates. As shown in
Figure 6.1, we can express the mapping between a world space quadrilateral and the
standard region quadrilateral on [-1,1] × [-1,1] via a bi-linear mapping function
χ(
j is a n-tuple
of dimension d denoting the dimension in which the points are specified in world
space. For example, when considering a quadrilateral on the 2D plane, our vertex
points each contain two coordinates denotes the x– and y–coordinates. As shown in
Figure 6.1, we can express the mapping between a world space quadrilateral and the
standard region quadrilateral on [-1,1] × [-1,1] via a bi-linear mapping function
χ(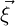 ).
).

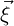 ) is a function of one variable and is merely
an affine mapping. In two dimensions, the mapping of a straight-sided triangle is a linear
mapping (i.e., P(1) in the language of traditional finite elements – a total degree k = 1
space) and the mapping of a straight-sided quadrilateral is a bi-linear mapping (i.e,
Q(1) in the language of traditional finite elements – a degree k = 1 map along each
coordinate direction combined through tensor-product). In three dimensions, the
mapping of a planar-sided tetrahedron is also a linear mapping, the mapping of a
planar-sided hexahedron is a tri-linear mapping, and the prism and pyramid are
mathematically somewhere in-between these two canonical types as given in
) is a function of one variable and is merely
an affine mapping. In two dimensions, the mapping of a straight-sided triangle is a linear
mapping (i.e., P(1) in the language of traditional finite elements – a total degree k = 1
space) and the mapping of a straight-sided quadrilateral is a bi-linear mapping (i.e,
Q(1) in the language of traditional finite elements – a degree k = 1 map along each
coordinate direction combined through tensor-product). In three dimensions, the
mapping of a planar-sided tetrahedron is also a linear mapping, the mapping of a
planar-sided hexahedron is a tri-linear mapping, and the prism and pyramid are
mathematically somewhere in-between these two canonical types as given in 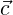 0 that informs the curve on edge 1. As shown in Figure
0 that informs the curve on edge 1. As shown in Figure 
 0 to specify the coefficient to be
used. In the figure, we assume that the form of the function is collocating, but in practice it
need not be so.
0 to specify the coefficient to be
used. In the figure, we assume that the form of the function is collocating, but in practice it
need not be so.
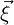 ), we
can now move to how we compute the geometric factors for regular as well as for deformed
mappings. We use the term “regular mappings" to refer to mappings from reference space
elements to world space elements with the same dimension. For instance, a collection of
triangles that lie in a plane can be represented by vertex coordinates that an only 2-tuples and
the mappings between the reference space triangle the and world space triangle does not need
to consider a larger embedded dimension. This was a fundamental assumption of the original
Nektar code: segments lived on the 1D line, triangles and quadrilaterals lived on the 2D plane
and that hexahedra, tetrahedra, etc., lived in the 3D volume. When redesigning
Nektar++, we purposefully enabled geometric entities to live in a high-dimensional
embedding space, different from their parameterized dimension. For instance, in
Nektar++, it is possible to define segment expansions (functions that live over one
dimensional parameterized curves) that are embedded in 3D. The same is true for
quadrilaterals and triangles – although their parameterized dimension is two, both
may live in a higher dimensional embedding space and thus represent a manifold of
co-dimension one in that space. For mappings that maintain the co-dimension is
the opposite of the dimension (i.e., quadrilateral in a plane represented by vertices
with two coordinates mapped to a two parameter reference quadrilateral), we keep
to the mapping conventions originally outlined in
), we
can now move to how we compute the geometric factors for regular as well as for deformed
mappings. We use the term “regular mappings" to refer to mappings from reference space
elements to world space elements with the same dimension. For instance, a collection of
triangles that lie in a plane can be represented by vertex coordinates that an only 2-tuples and
the mappings between the reference space triangle the and world space triangle does not need
to consider a larger embedded dimension. This was a fundamental assumption of the original
Nektar code: segments lived on the 1D line, triangles and quadrilaterals lived on the 2D plane
and that hexahedra, tetrahedra, etc., lived in the 3D volume. When redesigning
Nektar++, we purposefully enabled geometric entities to live in a high-dimensional
embedding space, different from their parameterized dimension. For instance, in
Nektar++, it is possible to define segment expansions (functions that live over one
dimensional parameterized curves) that are embedded in 3D. The same is true for
quadrilaterals and triangles – although their parameterized dimension is two, both
may live in a higher dimensional embedding space and thus represent a manifold of
co-dimension one in that space. For mappings that maintain the co-dimension is
the opposite of the dimension (i.e., quadrilateral in a plane represented by vertices
with two coordinates mapped to a two parameter reference quadrilateral), we keep
to the mapping conventions originally outlined in 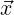 = xi and that our reference space coordinates are given by
= xi and that our reference space coordinates are given by 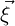 = ξj, there i and j run from
zero to dim - 1 where dim is the parameter dimension of the element (e.g. for a triangle,
dim = 2).
= ξj, there i and j run from
zero to dim - 1 where dim is the parameter dimension of the element (e.g. for a triangle,
dim = 2).

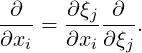
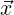 = xi and that our reference space coordinates are given by
= xi and that our reference space coordinates are given by 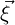 = ξj, there
i runs from zero to dim - 1 where dim is the embedding dimension and j runs
from zero to M - 1 where M is the parameter dimension of the element (e.g.for a
triangle on a manifold embedded in 3D with vertex values in 3D, dim = 3 whilst
M = 2).
= ξj, there
i runs from zero to dim - 1 where dim is the embedding dimension and j runs
from zero to M - 1 where M is the parameter dimension of the element (e.g.for a
triangle on a manifold embedded in 3D with vertex values in 3D, dim = 3 whilst
M = 2).