9.4 Preconditioners

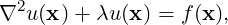
Most of the solvers in Nektar++, including the incompressible Navier-Stokes equations, rely on the solution of a Helmholtz equation,

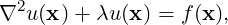(9.1)

an elliptic boundary value problem, at every time-step, where u is defined on a domain Ω of N_el non-overlapping elements. In this section, we outline the preconditioners which are implemented in Nektar++. Whilst some of the preconditioners are generic, many are especially designed for the modified basis only.

9.4.1 Mathematical formulation

The standard spectral/hp approach to discretise (9.1) starts with an expansion in terms of the elemental modes:

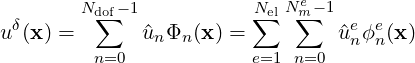(9.2)

where N_el is the number of elements, N_m^e is the number of local expansion modes within the element Ω^e, ϕ_n^e(x) is the n^th local expansion mode within the element Ω^e, û_n^e is the n^th local expansion coefficient within the element Ω^e. Approximating our solution by (9.2), we adopt a Galerkin discretisation of equation (9.1) where for an appropriate test space V ^δ we find an approximate solution u^δ ∈ V ^δ such that

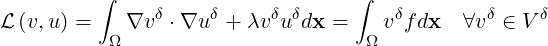
This can be formulated in matrix terms as

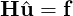
where H represents the Helmholtz matrix, 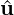are the unknown global coefficients and f the inner product the expansion basis with the forcing function.

C⁰ formulation

We first consider the C⁰ (i.e. continuous Galerkin) formulation. The spectral/hp expansion basis is obtained by considering interior modes, which have support in the interior of the element, separately from boundary modes which are non-zero on the boundary of the element. We align the boundary modes across the interface of the elements to obtain a continuous global solution. The boundary modes can be further decomposed into vertex, edge and face modes, defined as follows:

• vertex modes have support on a single vertex and the three adjacent edges and faces as well as the interior of the element;
• edge modes have support on a single edge and two adjacent faces as well as the interior of the element;
• face modes have support on a single face and the interior of the element.

When the discretisation is continuous, this strong coupling between vertices, edges and faces leads to a matrix of high condition number κ. Our aim is to reduce this condition number by applying specialised preconditioners. Utilising the above mentioned decomposition, we can write the matrix equation as:

where the subscripts b and i denote the boundary and interior degrees of freedom respectively. This system then can be statically condensed allowing us to solve for the boundary and interior degrees of freedom in a decoupled manor. The statically condensed matrix is given by

This is highly advantageous since by definition of our interior expansion this vanishes on the boundary, and so H_ii is block diagonal and thus can be easily inverted. The above sub-structuring has reduced our problem to solving the boundary problem:

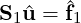
where S₁ = H_bb -H_biH_ii^-1H_ib and 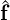₁ = 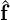_b -H_biH_ii^-1 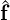_i. Although this new system typically has better convergence properties (i.e lower κ), the system is still ill-conditioned, leading to a convergence rate of the conjugate gradient (CG) routine that is prohibitively slow. For this reason we need to precondition S₁. To do this we solve an equivalent system of the form:

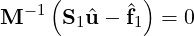
where the preconditioning matrix M is such that κ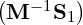 is less than κ and speeds up the convergence rate. Within the conjugate gradient routine the same preconditioner M is applied to the residual vector 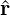_k+1 of the CG routine every iteration:

HDG formulation

When utilising a hybridizable discontinuous Galerkin formulation, we perform a static condensation approach but in a discontinuous framework, which for brevity we omit here. However, we still obtain a matrix equation of the form

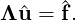
where Λ represents an operator which projects the solution of each face back onto the three-dimensional element or edge onto the two-dimensional element. In this setting then, consists of degrees of freedom for each egde (in 2D) or face (in 3D). The overall system does not, therefore, results in a weaker coupling between degrees of freedom, but at the expense of a larger matrix system.

9.4.2 Preconditioners

Within the Nektar++ framework a number of preconditioners are available to speed up the convergence rate of the conjugate gradient routine. The table below summarises each method, the dimensions of elements which are supported, and also the discretisation type support which can either be continuous (CG) or discontinuous (hybridizable DG).

The default is the Diagonal preconditioner. The above preconditioners are specified through the Preconditioner option of the SOLVERINFO section in the session file. For example, to enable FullLinearSpace one can use:

Alternatively one can have more control over different preconditioners for each solution field by using the GlobalSysSoln section. For more details, consult the user guide. The following sections specify the details for each method.

Diagonal

Diagonal (or Jacobi) preconditioning is amongst the simplest preconditioning strategies. In this scheme one takes the global matrix H = (h_ij) and computes the diagonal terms h_ii. The preconditioner is then formed as a diagonal matrix M^-1 = (h_ii^-1).

Linear space

The linear space (or coarse space) of the matrix system is that containing degrees of freedom corresponding only to the vertex modes in the high-order system. Preconditioning of this space is achieved by forming the matrix corresponding to the coarse space and inverting it, so that

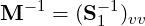
Since the mesh associated with higher order methods is relatively coarse compared with traditional finite element discretisations, the linear space can usually be directly inverted without memory issues. However such a methodology can be prohibitive on large parallel systems, due to a bottleneck in communication.

In Nektar++ the inversion of the linear space present is handled using the XX^T library. XX^T is a parallel direct solver for problems of the form A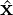 = 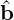based around a sparse factorisation of the inverse of A. To precondition utilising this methodology the linear sub-space is gathered from the expansion and the preconditioned residual within the CG routine is determined by solving

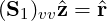
The preconditioned residual 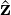is then scattered back to the respective location in the global degrees of freedom.

Block

Block preconditioning of the C⁰ continuous system is defined by the following:

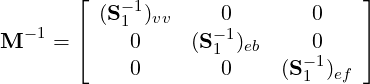
where diag[(S₁)_vv] is the diagonal of the vertex modes, (S₁)_eb and (S₁)_fb are block diagonal matrices corresponding to coupling of an edge (or face) with itself i.e ignoring the coupling to other edges and faces. This preconditioner is best suited for two dimensional problems.

In the HDG system, we take the block corresponding to each face and invert it. Each of these inverse blocks then forms one of the diagonal components of the block matrix M^-1.

Applied to the full matrix system H, the preconditioner additionally includes the inverse of the interior modes H_ii and is defined by:

9.4.3 Low energy

Low energy basis preconditioning follows the methodology proposed by Sherwin & Casarin. In this method a new basis is numerically constructed from the original basis which allows the Schur complement matrix to be preconditioned using a block preconditioner. The method is outlined briefly in the following.

Elementally the local approximation u^δ can be expressed as different expansions lying in the same discrete space V ^δ

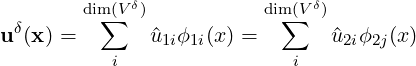
Since both expansions lie in the same space it’s possible to express one basis in terms of the other via a transformation, i.e.

Applying this to the Helmholtz operator it is possible to show that,

For sub-structured matrices (S) the transformation matrix (C) becomes:

Hence the transformation in terms of the Schur complement matrices is:

Typically the choice of expansion basis ϕ₁ can lead to a Helmholtz matrix that has undesirable properties i.e poor condition number. By choosing a suitable transformation matrix C it is possible to construct a new basis, numerically, that is amenable to block diagonal preconditioning.

Applying the transformation S₂ = RS₁R^T leads to the following matrix

where AS_ef,efA^T is given by

To orthogonalise the vertex-edge and vertex-face modes, it can be seen from the above that

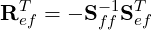
and for the edge-face modes:

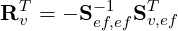
Here it is important to consider the form of the expansion basis since the presence of S_ff^-1 will lead to a new basis which has support on all other faces; this is problematic when creating a C⁰ continuous global basis. To circumvent this problem when forming the new basis, the decoupling is only performed between a specific edge and the two adjacent faces in a symmetric standard region. Since the decoupling is performed in a rotationally symmetric standard region the basis does not take into account the Jacobian mapping between the local element and global coordinates, hence the final expansion will not be completely orthogonal.

The low energy basis creates a Schur complement matrix that although it is not completely orthogonal can be spectrally approximated by its block diagonal contribution. The final form of the preconditioner is:

where diag[(S₂)_vv] is the diagonal of the vertex modes, (S₂)_eb and (S₂)_fb are block diagonal matrices corresponding to coupling of an edge (or face) with itself i.e ignoring the coupling to other edges and faces.