
Based upon the appendix in [18], we outline a rigorous derivation of the Laplace-Beltrami operator. We use the convention that indices appearing once in the upper position and once in the lower position are considered dummy indices and are implicitly summed over their range, while non-repeated indices are considered free to take any value. Derivatives are also denoted using the lower-index comma notation, for example gij,k. Covariant vectors such as the gradient are those which, under a change of coordinate system, change under the same transformation in order to maintain coordinate system invariance. In contrast, contravariant vectors, such as velocity, should remain fixed under a coordinate transformation requiring that their components change under the inverse of the transformation to maintain invariance. With this in mind, we now construct the fundamental differential operators we require for a 2-dimensional manifold embedded in a 3-dimensional space. In order to express these operators in curvilinear coordinates we start by assuming that we have a smooth surface parametrization given by
| x(ξ1,ξ2) := (x1(ξ1,ξ2),x2(ξ1,ξ2),x3(ξ1,ξ2)). |
Next we will define the Jacobian of x as the tensor
Jij =  |
where Jij can be viewed as a covariant surface vector (by fixing the upper index) or as a contravariant space vector (by fixing the lower index). The surface metric tensor gij can be defined in terms of the Jij as
| gij = ∑ k=13J ikJ jk. | (10.1) |
which can be considered to transform a contravariant quantity to a covariant quantity. Similarly the conjugate tensor gij, which does the reverse transformation, is given by
| g11 = g 22∕g, g12 = g21 = -g 12∕g, g22 = g 11∕g, | (10.2) |
where g is the determinant of gij. The metric tensor and its conjugate satisfy the condition
δij = g
ikgjk = 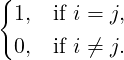 |
To construct the divergence operator we will also need the derivative of g with respect to
components of the metric, gij. We know that g is invertible and from linear algebra we have
that the inverse of the metric (10.2) satisfies g-1 = 
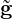 ⊤, where
⊤, where 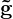 is the cofactor matrix of g.
Therefore
is the cofactor matrix of g.
Therefore  ⊤ = gg-1, or in components
⊤ = gg-1, or in components 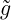 ij = g(g-1)ji. Using Jacobi’s formula for the
derivative of a matrix determinant with respect its entries, and since g is invertible, the
derivative of the metric determinant is
ij = g(g-1)ji. Using Jacobi’s formula for the
derivative of a matrix determinant with respect its entries, and since g is invertible, the
derivative of the metric determinant is
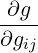 = tr = tr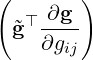 = = 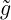 ij = g(g-1)
ji = ggij. ij = g(g-1)
ji = ggij. | (10.3) |
The partial derivative of a tensor with respect to a manifold coordinate system is itself not a tensor. In order to obtain a tensor, one has to use covariant derivative, defined below. The covariant derivative of a contravariant vector is given by
| ∇kai = a ,ki + ajΓ jki. | (10.4) |
where Γjki are Christoffel Symbols of the second kind. The Christoffel symbols of the first kind are defined by
Γijk =  ![[g + g - g ]
kj,i ik,j ij,k](developer-guide186x.png) . . |
Here we note that Γijk is symmetric in the first two indices. To obtain the Christoffel symbols of the second kind we formally raise the last index using the conjugate tensor,
| Γijl = Γ ijkgkl | (10.5) |
which retains the symmetry in the lower two indices. We can now express the derivatives of the metric tensor in terms of the Christoffel symbols as
| gij,k = Γikj + Γjki = gljΓikl + g liΓjkl. |
We now define the divergence operator on the manifold, ∇⋅X = ∇kXk. Consider first the derivative of the determinant of the metric tensor g with respect to the components of some local coordinates system ξ1,ξ2. We apply the chain rule, making use of the derivative of the metric tensor with respect to components of the metric (10.3) and the relationship (10.5), to get
 = = 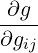 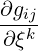 = ggijg
ij,k = ggij(Γ
ikj + Γjki) = g(Γiki + Γ
jkj) = 2gΓ
iki. = ggijg
ij,k = ggij(Γ
ikj + Γjki) = g(Γiki + Γ
jkj) = 2gΓ
iki. | (10.6) |
We can therefore express the Christoffel symbol Γiki in terms of this derivative as
Γiki = 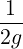 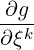 = = 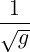 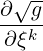 . . | (10.7) |
Finally, by substituting for Γiki in the expression for the divergence operator
| ∇kXk | = X ,kk + XiΓ kik | ||
| = X,kk + XkΓ iki | |||
= X,kk + Xk ( ( )
,k )
,k |
we can deduce a formula for divergence of a contravariant vector as
∇⋅X = ∇kXk =  | (10.8) |
The covariant derivative (gradient) of a scalar on the manifold is identical to the partial derivative, ∇kϕ = ϕ,k. To derive the Laplacian operator we need the contravariant form of the covariant gradient above which can be found by raising the index using the metric tensor, giving
| ∇kϕ = gkjϕ ,j, | (10.9) |
and substituting (10.9) for Xk in (10.8) to get the Laplacian operator on the manifold as
ΔMϕ = 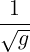 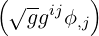 ,i. ,i. | (10.10) |
We now extend the above operator to allow for anisotropic diffusion in the domain by
deriving an expression for the surface conductivity from the ambient conductivity. The
gradient of a surface function scaled by the ambient conductivity tensor  p is given
by
p is given
by
 pf = gmpJ
mlσ
klJjkgij pf = gmpJ
mlσ
klJjkgij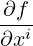 . . | (10.11) |
The surface gradient is mapped to the ambient space through the Jacobian Jjk, scaled by the ambient conductivity, and mapped back to the surface through Jml. The anisotropic Laplacian operator is given by
 2f = ∇
k 2f = ∇
k kf = ∇k kf = ∇k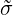 ij∇jf ij∇jf | (10.12) |
Therefore the surface conductivity tensor can be computed using the Jacobian tensor and the inverse metric as
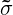 = g-1JσJ⊤g-1. = g-1JσJ⊤g-1. | (10.13) |
Anisotropic diffusion is important in many applications. In the ambient Euclidean space, this can be represented by a diffusivity tensor σ in the Laplacian operator as
| ΔM = ∇⋅ σ∇. |
On our manifold, we seek the generalisation of 10.10, in the form
 Mϕ = ∇j Mϕ = ∇j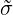 ij∇iϕ. ij∇iϕ. |
where the 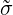 ij are entries in the surface diffusivity. For a contravariant surface vector aj we can
find the associated space vector Ai as Ai = Jjiaj. Similarly if Ai is a covariant space vector,
then aj = JjiAi is a covariant surface vector. Using these we can construct the anisotropic
diffusivity tensor
ij are entries in the surface diffusivity. For a contravariant surface vector aj we can
find the associated space vector Ai as Ai = Jjiaj. Similarly if Ai is a covariant space vector,
then aj = JjiAi is a covariant surface vector. Using these we can construct the anisotropic
diffusivity tensor 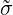 on the manifold by constraining the ambient diffusivity tensor σ to the
surface. The contravariant surface gradient ∇iϕ is mapped to the corresponding space vector,
which lies in the tangent plane to the surface. This is scaled by the ambient diffusivity and
then projected back to a covariant surface vector. Finally, we use the conjugate
metric to convert back to a contravariant form. The resulting surface Laplacian
is
on the manifold by constraining the ambient diffusivity tensor σ to the
surface. The contravariant surface gradient ∇iϕ is mapped to the corresponding space vector,
which lies in the tangent plane to the surface. This is scaled by the ambient diffusivity and
then projected back to a covariant surface vector. Finally, we use the conjugate
metric to convert back to a contravariant form. The resulting surface Laplacian
is
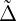 Mϕ = ∇mglmJ
lkσ
jkJij∇iϕ. Mϕ = ∇mglmJ
lkσ
jkJij∇iϕ. |
Following on from this we deduce that
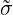 ij = gjmJ
mlσ
lkJik. ij = gjmJ
mlσ
lkJik. |
It can be seen that in the case of isotropic diffusion that 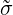 ij = δji ⇔ σ = I,
ij = δji ⇔ σ = I,
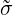 ij = gimJ
mkσ
lkJjl = gimJ
mkJ
jk = gimg
mj = δji. ij = gimJ
mkσ
lkJjl = gimJ
mkJ
jk = gimg
mj = δji. |