Nektar++
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
Static Public Member Functions | Public Attributes | Static Public Attributes | Protected Member Functions | Protected Attributes | List of all members
Nektar::SolverUtils::AdvectionFR Class Reference

#include <AdvectionFR.h>

Inheritance diagram for Nektar::SolverUtils::AdvectionFR:
Inheritance graph
[legend]
Collaboration diagram for Nektar::SolverUtils::AdvectionFR:
Collaboration graph
[legend]

Static Public Member Functions

static AdvectionSharedPtr create (std::string advType)

Public Attributes

Array< OneD, NekDouble > m_jac
Array< OneD, Array< OneD,
NekDouble > > 		m_gmat
Array< OneD, Array< OneD,
NekDouble > > 		m_Q2D_e0
Array< OneD, Array< OneD,
NekDouble > > 		m_Q2D_e1
Array< OneD, Array< OneD,
NekDouble > > 		m_Q2D_e2
Array< OneD, Array< OneD,
NekDouble > > 		m_Q2D_e3
Array< OneD, Array< OneD,
NekDouble > > 		m_dGL_xi1
Array< OneD, Array< OneD,
NekDouble > > 		m_dGR_xi1
Array< OneD, Array< OneD,
NekDouble > > 		m_dGL_xi2
Array< OneD, Array< OneD,
NekDouble > > 		m_dGR_xi2
Array< OneD, Array< OneD,
NekDouble > > 		m_dGL_xi3
Array< OneD, Array< OneD,
NekDouble > > 		m_dGR_xi3
DNekMatSharedPtr m_Ixm
DNekMatSharedPtr m_Ixp

Static Public Attributes

static std::string type []

Protected Member Functions

 AdvectionFR (std::string advType)
 AdvectionFR uses the Flux Reconstruction (FR) approach to compute the advection term. The implementation is only for segments, quadrilaterals and hexahedra at the moment.
virtual void v_InitObject (LibUtilities::SessionReaderSharedPtr pSession, Array< OneD, MultiRegions::ExpListSharedPtr > pFields)
 Initiliase AdvectionFR objects and store them before starting the time-stepping.
virtual void v_Advect (const int nConvectiveFields, const Array< OneD, MultiRegions::ExpListSharedPtr > &fields, const Array< OneD, Array< OneD, NekDouble > > &advVel, const Array< OneD, Array< OneD, NekDouble > > &inarray, Array< OneD, Array< OneD, NekDouble > > &outarray)
 Compute the advection term at each time-step using the Flux Reconstruction approach (FR).
virtual void v_SetupMetrics (LibUtilities::SessionReaderSharedPtr pSession, Array< OneD, MultiRegions::ExpListSharedPtr > pFields)
 Setup the metric terms to compute the contravariant fluxes. (i.e. this special metric terms transform the fluxes at the interfaces of each element from the physical space to the standard space).
virtual void v_SetupCFunctions (LibUtilities::SessionReaderSharedPtr pSession, Array< OneD, MultiRegions::ExpListSharedPtr > pFields)
 Setup the derivatives of the correction functions. For more details see J Sci Comput (2011) 47: 50–72.
virtual void v_DivCFlux_1D (const int nConvectiveFields, const Array< OneD, MultiRegions::ExpListSharedPtr > &fields, const Array< OneD, const NekDouble > &fluxX1, const Array< OneD, const NekDouble > &numericalFlux, Array< OneD, NekDouble > &divCFlux)
 Compute the divergence of the corrective flux for 1D problems.
virtual void v_DivCFlux_2D (const int nConvectiveFields, const Array< OneD, MultiRegions::ExpListSharedPtr > &fields, const Array< OneD, const NekDouble > &fluxX1, const Array< OneD, const NekDouble > &fluxX2, const Array< OneD, const NekDouble > &numericalFlux, Array< OneD, NekDouble > &divCFlux)
 Compute the divergence of the corrective flux for 2D problems.
virtual void v_DivCFlux_2D_Gauss (const int nConvectiveFields, const Array< OneD, MultiRegions::ExpListSharedPtr > &fields, const Array< OneD, const NekDouble > &fluxX1, const Array< OneD, const NekDouble > &fluxX2, const Array< OneD, const NekDouble > &numericalFlux, Array< OneD, NekDouble > &divCFlux)
 Compute the divergence of the corrective flux for 2D problems where POINTSTYPE="GaussGaussLegendre".
virtual void v_DivCFlux_3D (const int nConvectiveFields, const Array< OneD, MultiRegions::ExpListSharedPtr > &fields, const Array< OneD, const NekDouble > &fluxX1, const Array< OneD, const NekDouble > &fluxX2, const Array< OneD, const NekDouble > &fluxX3, const Array< OneD, const NekDouble > &numericalFlux, Array< OneD, NekDouble > &divCFlux)
 Compute the divergence of the corrective flux for 3D problems.

Protected Attributes

Array< OneD, Array< OneD,
NekDouble > > 		m_traceNormals
std::string m_advType
- Protected Attributes inherited from Nektar::SolverUtils::Advection
AdvectionFluxVecCB m_fluxVector
 Callback function to the flux vector (set when advection is in conservative form).
RiemannSolverSharedPtr m_riemann
 Riemann solver for DG-type schemes.
int m_spaceDim
 Storage for space dimension. Used for homogeneous extension.

Additional Inherited Members

- Public Member Functions inherited from Nektar::SolverUtils::Advection
SOLVER_UTILS_EXPORT void InitObject (LibUtilities::SessionReaderSharedPtr pSession, Array< OneD, MultiRegions::ExpListSharedPtr > pFields)
SOLVER_UTILS_EXPORT void Advect (const int nConvectiveFields, const Array< OneD, MultiRegions::ExpListSharedPtr > &fields, const Array< OneD, Array< OneD, NekDouble > > &advVel, const Array< OneD, Array< OneD, NekDouble > > &inarray, Array< OneD, Array< OneD, NekDouble > > &outarray)
template<typename FuncPointerT , typename ObjectPointerT >
void SetFluxVector (FuncPointerT func, ObjectPointerT obj)
 Set the flux vector callback function.
void SetRiemannSolver (RiemannSolverSharedPtr riemann)
 Set a Riemann solver object for this advection object.
void SetFluxVector (AdvectionFluxVecCB fluxVector)
 Set the flux vector callback function.

Detailed Description

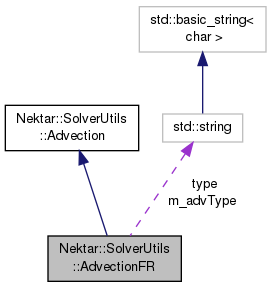
Definition at line 47 of file AdvectionFR.h.

Constructor & Destructor Documentation

Nektar::SolverUtils::AdvectionFR::AdvectionFR ( std::string  advType)
protected

AdvectionFR uses the Flux Reconstruction (FR) approach to compute the advection term. The implementation is only for segments, quadrilaterals and hexahedra at the moment.

Todo:
Extension to triangles, tetrahedra and other shapes. (Long term objective)

Definition at line 75 of file AdvectionFR.cpp.

Referenced by create().

:m_advType(advType)
{
}

Member Function Documentation

static AdvectionSharedPtr Nektar::SolverUtils::AdvectionFR::create ( std::string  advType)
inlinestatic

Definition at line 50 of file AdvectionFR.h.

References AdvectionFR().

{
return AdvectionSharedPtr(new AdvectionFR(advType));
}
void Nektar::SolverUtils::AdvectionFR::v_Advect ( const int  nConvectiveFields,
const Array< OneD, MultiRegions::ExpListSharedPtr > &  fields,
const Array< OneD, Array< OneD, NekDouble > > &  advVel,
const Array< OneD, Array< OneD, NekDouble > > &  inarray,
Array< OneD, Array< OneD, NekDouble > > &  outarray 
)
protectedvirtual

Compute the advection term at each time-step using the Flux Reconstruction approach (FR).

Parameters
nConvectiveFieldsNumber of fields.
fieldsPointer to fields.
advVelAdvection velocities.
inarraySolution at the previous time-step.
outarrayAdvection term to be passed at the time integration class.

Implements Nektar::SolverUtils::Advection.

Definition at line 797 of file AdvectionFR.cpp.

References ASSERTL0, Nektar::LibUtilities::eGaussGaussLegendre, Nektar::SolverUtils::Advection::m_fluxVector, m_gmat, m_jac, Nektar::SolverUtils::Advection::m_riemann, Nektar::SolverUtils::Advection::m_spaceDim, v_DivCFlux_1D(), v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), Vmath::Vadd(), Vmath::Vdiv(), Vmath::Vmul(), and Vmath::Vvtvvtp().

{
int i, j, n;
int phys_offset;
Array<OneD, NekDouble> auxArray1, auxArray2;
Array<OneD, LibUtilities::BasisSharedPtr> Basis;
Basis = fields[0]->GetExp(0)->GetBase();
int nElements = fields[0]->GetExpSize();
int nDimensions = fields[0]->GetCoordim(0);
int nSolutionPts = fields[0]->GetTotPoints();
int nTracePts = fields[0]->GetTrace()->GetTotPoints();
int nCoeffs = fields[0]->GetNcoeffs();
// Storage for flux vector.
Array<OneD, Array<OneD, Array<OneD, NekDouble> > > fluxvector
(nConvectiveFields);
// Outarray for Galerkin projection in case of primitive dealising
Array<OneD, Array<OneD, NekDouble> > outarrayCoeff
(nConvectiveFields);
// Store forwards/backwards space along trace space
Array<OneD, Array<OneD, NekDouble> > Fwd (nConvectiveFields);
Array<OneD, Array<OneD, NekDouble> > Bwd (nConvectiveFields);
Array<OneD, Array<OneD, NekDouble> > numflux(nConvectiveFields);
// Set up storage for flux vector.
for (i = 0; i < nConvectiveFields; ++i)
{
fluxvector[i] =
Array<OneD, Array<OneD, NekDouble> >(m_spaceDim);
for (j = 0; j < m_spaceDim; ++j)
{
fluxvector[i][j] = Array<OneD, NekDouble>(nSolutionPts);
}
}
for (i = 0; i < nConvectiveFields; ++i)
{
outarrayCoeff[i] = Array<OneD, NekDouble>(nCoeffs);
Fwd[i] = Array<OneD, NekDouble>(nTracePts);
Bwd[i] = Array<OneD, NekDouble>(nTracePts);
numflux[i] = Array<OneD, NekDouble>(nTracePts);
fields[i]->GetFwdBwdTracePhys(inarray[i], Fwd[i], Bwd[i]);
}
// Computing the interface flux at each trace point
m_riemann->Solve(m_spaceDim, Fwd, Bwd, numflux);
// Divergence of the flux (computing the RHS)
switch(nDimensions)
{
// 1D problems
case 1:
{
Array<OneD, NekDouble> DfluxvectorX1(nSolutionPts);
Array<OneD, NekDouble> divFC (nSolutionPts);
// Get the advection flux vector (solver specific)
m_fluxVector(inarray, fluxvector);
// Get the discontinuous flux divergence
for(i = 0; i < nConvectiveFields; ++i)
{
for (n = 0; n < nElements; n++)
{
phys_offset = fields[0]->GetPhys_Offset(n);
fields[i]->GetExp(n)->PhysDeriv(
0, fluxvector[i][0] + phys_offset,
auxArray2 = DfluxvectorX1 + phys_offset);
}
// Get the correction flux divergence
v_DivCFlux_1D(nConvectiveFields, fields,
fluxvector[i][0], numflux[i], divFC);
// Back to the physical space using global operations
Vmath::Vdiv(nSolutionPts, &divFC[0], 1, &m_jac[0], 1,
&outarray[i][0], 1);
// Adding the total divergence to outarray (RHS)
Vmath::Vadd(nSolutionPts, &outarray[i][0], 1,
&DfluxvectorX1[0], 1, &outarray[i][0], 1);
// Primitive Dealiasing 1D
if (!(Basis[0]->Collocation()))
{
fields[i]->FwdTrans(outarray[i], outarrayCoeff[i]);
fields[i]->BwdTrans(outarrayCoeff[i], outarray[i]);
}
}
break;
}
// 2D problems
case 2:
{
Array<OneD, NekDouble> DfluxvectorX1(nSolutionPts);
Array<OneD, NekDouble> DfluxvectorX2(nSolutionPts);
Array<OneD, NekDouble> divFD(nSolutionPts);
Array<OneD, NekDouble> divFC(nSolutionPts);
// Get the advection flux vector (solver specific)
m_fluxVector(inarray, fluxvector);
for (i = 0; i < nConvectiveFields; ++i)
{
// Temporary vectors
Array<OneD, NekDouble> f_hat(nSolutionPts);
Array<OneD, NekDouble> g_hat(nSolutionPts);
Vmath::Vvtvvtp(nSolutionPts,
&m_gmat[0][0], 1,
&fluxvector[i][0][0], 1,
&m_gmat[2][0], 1,
&fluxvector[i][1][0], 1,
&f_hat[0], 1);
Vmath::Vmul(nSolutionPts, &m_jac[0], 1, &f_hat[0], 1,
&f_hat[0], 1);
Vmath::Vvtvvtp(nSolutionPts,
&m_gmat[1][0], 1,
&fluxvector[i][0][0], 1,
&m_gmat[3][0], 1,
&fluxvector[i][1][0], 1,
&g_hat[0], 1);
Vmath::Vmul(nSolutionPts, &m_jac[0], 1, &g_hat[0], 1,
&g_hat[0], 1);
// Get the discontinuous flux derivatives
for (n = 0; n < nElements; n++)
{
phys_offset = fields[0]->GetPhys_Offset(n);
fields[0]->GetExp(n)->StdPhysDeriv(0,
auxArray1 = f_hat + phys_offset,
auxArray2 = DfluxvectorX1 + phys_offset);
fields[0]->GetExp(n)->StdPhysDeriv(1,
auxArray1 = g_hat + phys_offset,
auxArray2 = DfluxvectorX2 + phys_offset);
}
// Divergence of the discontinuous flux
Vmath::Vadd(nSolutionPts, DfluxvectorX1, 1,
DfluxvectorX2, 1, divFD, 1);
// Divergence of the correction flux
if (Basis[0]->GetPointsType() ==
LibUtilities::eGaussGaussLegendre &&
Basis[1]->GetPointsType() ==
LibUtilities::eGaussGaussLegendre)
{
v_DivCFlux_2D_Gauss(
nConvectiveFields, fields, f_hat, g_hat,
numflux[i], divFC);
}
else
{
v_DivCFlux_2D(
nConvectiveFields, fields,
fluxvector[i][0], fluxvector[i][1],
numflux[i], divFC);
}
// Divergence of the final flux
Vmath::Vadd(nSolutionPts, divFD, 1, divFC, 1,
outarray[i], 1);
// Back to the physical space using a global operation
Vmath::Vdiv(nSolutionPts, &outarray[i][0], 1,
&m_jac[0], 1, &outarray[i][0], 1);
// Primitive Dealiasing 2D
if (!(Basis[0]->Collocation()))
{
fields[i]->FwdTrans(outarray[i], outarrayCoeff[i]);
fields[i]->BwdTrans(outarrayCoeff[i], outarray[i]);
}
} // close nConvectiveFields loop
break;
}
// 3D problems
case 3:
{
ASSERTL0(false,"3D FRDG case not implemented yet");
break;
}
}
}
void Nektar::SolverUtils::AdvectionFR::v_DivCFlux_1D ( const int  nConvectiveFields,
const Array< OneD, MultiRegions::ExpListSharedPtr > &  fields,
const Array< OneD, const NekDouble > &  fluxX1,
const Array< OneD, const NekDouble > &  numericalFlux,
Array< OneD, NekDouble > &  divCFlux 
)
protectedvirtual

Compute the divergence of the corrective flux for 1D problems.

Parameters
nConvectiveFieldsNumber of fields.
fieldsPointer to fields.
fluxX1X1-volumetric flux in physical space.
numericalFluxInterface flux in physical space.
divCFluxDivergence of the corrective flux.

Definition at line 1006 of file AdvectionFR.cpp.

References m_dGL_xi1, m_dGR_xi1, Vmath::Smul(), Vmath::Vadd(), and Vmath::Vcopy().

Referenced by v_Advect().

{
int n;
int nLocalSolutionPts, phys_offset, t_offset;
LibUtilities::BasisSharedPtr Basis;
Basis = fields[0]->GetExp(0)->GetBasis(0);
int nElements = fields[0]->GetExpSize();
int nSolutionPts = fields[0]->GetTotPoints();
vector<bool> negatedFluxNormal = (boost::static_pointer_cast<MultiRegions::DisContField1D>(fields[0]))->GetNegatedFluxNormal();
// Arrays to store the derivatives of the correction flux
Array<OneD, NekDouble> DCL(nSolutionPts/nElements, 0.0);
Array<OneD, NekDouble> DCR(nSolutionPts/nElements, 0.0);
// Arrays to store the intercell numerical flux jumps
Array<OneD, NekDouble> JumpL(nElements);
Array<OneD, NekDouble> JumpR(nElements);
Array<OneD, Array<OneD, StdRegions::StdExpansionSharedPtr> >
&elmtToTrace = fields[0]->GetTraceMap()->GetElmtToTrace();
for (n = 0; n < nElements; ++n)
{
nLocalSolutionPts = fields[0]->GetExp(n)->GetTotPoints();
phys_offset = fields[0]->GetPhys_Offset(n);
Array<OneD, NekDouble> tmparrayX1(nLocalSolutionPts, 0.0);
NekDouble tmpFluxVertex = 0;
Vmath::Vcopy(nLocalSolutionPts,
&fluxX1[phys_offset], 1,
&tmparrayX1[0], 1);
fields[0]->GetExp(n)->GetVertexPhysVals(0, tmparrayX1,
tmpFluxVertex);
t_offset = fields[0]->GetTrace()
->GetPhys_Offset(elmtToTrace[n][0]->GetElmtId());
if(negatedFluxNormal[2*n])
{
JumpL[n] = numericalFlux[t_offset] - tmpFluxVertex;
}
else
{
JumpL[n] = -numericalFlux[t_offset] - tmpFluxVertex;
}
fields[0]->GetExp(n)->GetVertexPhysVals(1, tmparrayX1,
tmpFluxVertex);
t_offset = fields[0]->GetTrace()
->GetPhys_Offset(elmtToTrace[n][1]->GetElmtId());
if(negatedFluxNormal[2*n+1])
{
JumpR[n] = -numericalFlux[t_offset] - tmpFluxVertex;
}
else
{
JumpR[n] = numericalFlux[t_offset] - tmpFluxVertex;
}
}
for (n = 0; n < nElements; ++n)
{
nLocalSolutionPts = fields[0]->GetExp(n)->GetTotPoints();
phys_offset = fields[0]->GetPhys_Offset(n);
// Left jump multiplied by left derivative of C function
Vmath::Smul(nLocalSolutionPts, JumpL[n], &m_dGL_xi1[n][0], 1,
&DCL[0], 1);
// Right jump multiplied by right derivative of C function
Vmath::Smul(nLocalSolutionPts, JumpR[n], &m_dGR_xi1[n][0], 1,
&DCR[0], 1);
// Assembling divergence of the correction flux
Vmath::Vadd(nLocalSolutionPts, &DCL[0], 1, &DCR[0], 1,
&divCFlux[phys_offset], 1);
}
}
void Nektar::SolverUtils::AdvectionFR::v_DivCFlux_2D ( const int  nConvectiveFields,
const Array< OneD, MultiRegions::ExpListSharedPtr > &  fields,
const Array< OneD, const NekDouble > &  fluxX1,
const Array< OneD, const NekDouble > &  fluxX2,
const Array< OneD, const NekDouble > &  numericalFlux,
Array< OneD, NekDouble > &  divCFlux 
)
protectedvirtual

Compute the divergence of the corrective flux for 2D problems.

Parameters
nConvectiveFieldsNumber of fields.
fieldsPointer to fields.
fluxX1X1-volumetric flux in physical space.
fluxX2X2-volumetric flux in physical space.
numericalFluxInterface flux in physical space.
divCFluxDivergence of the corrective flux.
Todo:
: Switch on shapes eventually here.

Definition at line 1109 of file AdvectionFR.cpp.

References ASSERTL0, Nektar::StdRegions::eBackwards, m_dGL_xi1, m_dGL_xi2, m_dGR_xi1, m_dGR_xi2, m_Q2D_e0, m_Q2D_e1, m_Q2D_e2, m_Q2D_e3, m_traceNormals, Vmath::Reverse(), Vmath::Vadd(), Vmath::Vsub(), and Vmath::Vvtvvtp().

Referenced by v_Advect().

{
int n, e, i, j, cnt;
int nElements = fields[0]->GetExpSize();
int nLocalSolutionPts, nEdgePts;
int trace_offset, phys_offset;
int nquad0, nquad1;
Array<OneD, NekDouble> auxArray1;
Array<OneD, LibUtilities::BasisSharedPtr> base;
Array<OneD, Array<OneD, StdRegions::StdExpansionSharedPtr> >
&elmtToTrace = fields[0]->GetTraceMap()->GetElmtToTrace();
// Loop on the elements
for(n = 0; n < nElements; ++n)
{
// Offset of the element on the global vector
phys_offset = fields[0]->GetPhys_Offset(n);
nLocalSolutionPts = fields[0]->GetExp(n)->GetTotPoints();
base = fields[0]->GetExp(n)->GetBase();
nquad0 = base[0]->GetNumPoints();
nquad1 = base[1]->GetNumPoints();
Array<OneD, NekDouble> divCFluxE0(nLocalSolutionPts, 0.0);
Array<OneD, NekDouble> divCFluxE1(nLocalSolutionPts, 0.0);
Array<OneD, NekDouble> divCFluxE2(nLocalSolutionPts, 0.0);
Array<OneD, NekDouble> divCFluxE3(nLocalSolutionPts, 0.0);
// Loop on the edges
for(e = 0; e < fields[0]->GetExp(n)->GetNedges(); ++e)
{
// Number of edge points of edge e
nEdgePts = fields[0]->GetExp(n)->GetEdgeNumPoints(e);
Array<OneD, NekDouble> tmparrayX1(nEdgePts, 0.0);
Array<OneD, NekDouble> tmparrayX2(nEdgePts, 0.0);
Array<OneD, NekDouble> fluxN (nEdgePts, 0.0);
Array<OneD, NekDouble> fluxT (nEdgePts, 0.0);
Array<OneD, NekDouble> fluxJumps (nEdgePts, 0.0);
// Offset of the trace space correspondent to edge e
trace_offset = fields[0]->GetTrace()->GetPhys_Offset(
elmtToTrace[n][e]->GetElmtId());
// Get the normals of edge e
const Array<OneD, const Array<OneD, NekDouble> > &normals =
fields[0]->GetExp(n)->GetEdgeNormal(e);
// Extract the edge values of flux-x on edge e and order
// them accordingly to the order of the trace space
fields[0]->GetExp(n)->GetEdgePhysVals(
e, elmtToTrace[n][e],
fluxX1 + phys_offset,
auxArray1 = tmparrayX1);
// Extract the edge values of flux-y on edge e and order
// them accordingly to the order of the trace space
fields[0]->GetExp(n)->GetEdgePhysVals(
e, elmtToTrace[n][e],
fluxX2 + phys_offset,
auxArray1 = tmparrayX2);
// Multiply the edge components of the flux by the normal
Vmath::Vvtvvtp(nEdgePts, &tmparrayX1[0], 1,
&m_traceNormals[0][trace_offset], 1,
&tmparrayX2[0], 1,
&m_traceNormals[1][trace_offset], 1,
&fluxN[0], 1);
// Subtract to the Riemann flux the discontinuous flux
Vmath::Vsub(nEdgePts, &numericalFlux[trace_offset], 1,
&fluxN[0], 1, &fluxJumps[0], 1);
// Check the ordering of the jump vectors
if (fields[0]->GetExp(n)->GetEorient(e) ==
StdRegions::eBackwards)
{
Vmath::Reverse(nEdgePts, &fluxJumps[0], 1,
&fluxJumps[0], 1);
}
NekDouble fac = fields[0]->GetExp(n)->EdgeNormalNegated(e) ?
-1.0 : 1.0;
for (i = 0; i < nEdgePts; ++i)
{
if (m_traceNormals[0][trace_offset+i] != fac*normals[0][i]
|| m_traceNormals[1][trace_offset+i] != fac*normals[1][i])
{
fluxJumps[i] = -fluxJumps[i];
}
}
// Multiply jumps by derivatives of the correction functions
switch (e)
{
case 0:
for (i = 0; i < nquad0; ++i)
{
// Multiply fluxJumps by Q factors
fluxJumps[i] = -(m_Q2D_e0[n][i]) * fluxJumps[i];
for (j = 0; j < nquad1; ++j)
{
cnt = i + j*nquad0;
divCFluxE0[cnt] = fluxJumps[i] * m_dGL_xi2[n][j];
}
}
break;
case 1:
for (i = 0; i < nquad1; ++i)
{
// Multiply fluxJumps by Q factors
fluxJumps[i] = (m_Q2D_e1[n][i]) * fluxJumps[i];
for (j = 0; j < nquad0; ++j)
{
cnt = (nquad0)*i + j;
divCFluxE1[cnt] = fluxJumps[i] * m_dGR_xi1[n][j];
}
}
break;
case 2:
for (i = 0; i < nquad0; ++i)
{
// Multiply fluxJumps by Q factors
fluxJumps[i] = (m_Q2D_e2[n][i]) * fluxJumps[i];
for (j = 0; j < nquad1; ++j)
{
cnt = (nquad0 - 1) + j*nquad0 - i;
divCFluxE2[cnt] = fluxJumps[i] * m_dGR_xi2[n][j];
}
}
break;
case 3:
for (i = 0; i < nquad1; ++i)
{
// Multiply fluxJumps by Q factors
fluxJumps[i] = -(m_Q2D_e3[n][i]) * fluxJumps[i];
for (j = 0; j < nquad0; ++j)
{
cnt = (nquad0*nquad1 - nquad0) + j - i*nquad0;
divCFluxE3[cnt] = fluxJumps[i] * m_dGL_xi1[n][j];
}
}
break;
default:
ASSERTL0(false,"edge value (< 3) is out of range");
break;
}
}
// Sum each edge contribution
Vmath::Vadd(nLocalSolutionPts, &divCFluxE0[0], 1,
&divCFluxE1[0], 1, &divCFlux[phys_offset], 1);
Vmath::Vadd(nLocalSolutionPts, &divCFlux[phys_offset], 1,
&divCFluxE2[0], 1, &divCFlux[phys_offset], 1);
Vmath::Vadd(nLocalSolutionPts, &divCFlux[phys_offset], 1,
&divCFluxE3[0], 1, &divCFlux[phys_offset], 1);
}
}
void Nektar::SolverUtils::AdvectionFR::v_DivCFlux_2D_Gauss ( const int  nConvectiveFields,
const Array< OneD, MultiRegions::ExpListSharedPtr > &  fields,
const Array< OneD, const NekDouble > &  fluxX1,
const Array< OneD, const NekDouble > &  fluxX2,
const Array< OneD, const NekDouble > &  numericalFlux,
Array< OneD, NekDouble > &  divCFlux 
)
protectedvirtual

Compute the divergence of the corrective flux for 2D problems where POINTSTYPE="GaussGaussLegendre".

Parameters
nConvectiveFieldsNumber of fields.
fieldsPointer to fields.
fluxX1X1-volumetric flux in physical space.
fluxX2X2-volumetric flux in physical space.
numericalFluxInterface flux in physical space.
divCFluxDivergence of the corrective flux.
Todo:
: Switch on shapes eventually here.

Definition at line 1298 of file AdvectionFR.cpp.

References ASSERTL0, Nektar::StdRegions::eBackwards, m_dGL_xi1, m_dGL_xi2, m_dGR_xi1, m_dGR_xi2, m_Q2D_e0, m_Q2D_e1, m_Q2D_e2, m_Q2D_e3, m_traceNormals, Vmath::Neg(), Vmath::Reverse(), Vmath::Vadd(), Vmath::Vcopy(), and Vmath::Vsub().

Referenced by v_Advect().

{
int n, e, i, j, cnt;
int nElements = fields[0]->GetExpSize();
int nLocalSolutionPts;
int nEdgePts;
int trace_offset;
int phys_offset;
int nquad0;
int nquad1;
NekDouble fac;
Array<OneD, NekDouble> auxArray1, auxArray2;
Array<OneD, LibUtilities::BasisSharedPtr> base;
Array<OneD, Array<OneD, StdRegions::StdExpansionSharedPtr> >
&elmtToTrace = fields[0]->GetTraceMap()->GetElmtToTrace();
// Loop on the elements
for(n = 0; n < nElements; ++n)
{
// Offset of the element on the global vector
phys_offset = fields[0]->GetPhys_Offset(n);
nLocalSolutionPts = fields[0]->GetExp(n)->GetTotPoints();
base = fields[0]->GetExp(n)->GetBase();
nquad0 = base[0]->GetNumPoints();
nquad1 = base[1]->GetNumPoints();
Array<OneD, NekDouble> divCFluxE0(nLocalSolutionPts, 0.0);
Array<OneD, NekDouble> divCFluxE1(nLocalSolutionPts, 0.0);
Array<OneD, NekDouble> divCFluxE2(nLocalSolutionPts, 0.0);
Array<OneD, NekDouble> divCFluxE3(nLocalSolutionPts, 0.0);
// Loop on the edges
for(e = 0; e < fields[0]->GetExp(n)->GetNedges(); ++e)
{
// Number of edge points of edge e
nEdgePts = fields[0]->GetExp(n)->GetEdgeNumPoints(e);
Array<OneD, NekDouble> fluxN (nEdgePts, 0.0);
Array<OneD, NekDouble> fluxT (nEdgePts, 0.0);
Array<OneD, NekDouble> fluxN_R (nEdgePts, 0.0);
Array<OneD, NekDouble> fluxN_D (nEdgePts, 0.0);
Array<OneD, NekDouble> fluxJumps (nEdgePts, 0.0);
// Offset of the trace space correspondent to edge e
trace_offset = fields[0]->GetTrace()->GetPhys_Offset(
elmtToTrace[n][e]->GetElmtId());
// Get the normals of edge e
const Array<OneD, const Array<OneD, NekDouble> > &normals =
fields[0]->GetExp(n)->GetEdgeNormal(e);
// Extract the trasformed normal flux at each edge
switch (e)
{
case 0:
// Extract the edge values of transformed flux-y on
// edge e and order them accordingly to the order of
// the trace space
fields[0]->GetExp(n)->GetEdgePhysVals(
e, elmtToTrace[n][e],
fluxX2 + phys_offset,
auxArray1 = fluxN_D);
Vmath::Neg (nEdgePts, fluxN_D, 1);
// Extract the physical Rieamann flux at each edge
Vmath::Vcopy(nEdgePts,
&numericalFlux[trace_offset], 1,
&fluxN[0], 1);
// Check the ordering of vectors
if (fields[0]->GetExp(n)->GetEorient(e) ==
StdRegions::eBackwards)
{
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN, 1,
auxArray2 = fluxN, 1);
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN_D, 1,
auxArray2 = fluxN_D, 1);
}
// Transform Riemann Fluxes in the standard element
for (i = 0; i < nquad0; ++i)
{
// Multiply Riemann Flux by Q factors
fluxN_R[i] = (m_Q2D_e0[n][i]) * fluxN[i];
}
fac = fields[0]->GetExp(n)->EdgeNormalNegated(e) ?
-1.0 : 1.0;
for (i = 0; i < nEdgePts; ++i)
{
if (m_traceNormals[0][trace_offset+i]
!= fac*normals[0][i] ||
m_traceNormals[1][trace_offset+i]
!= fac*normals[1][i])
{
fluxN_R[i] = -fluxN_R[i];
}
}
// Subtract to the Riemann flux the discontinuous
// flux
Vmath::Vsub(nEdgePts,
&fluxN_R[0], 1,
&fluxN_D[0], 1, &fluxJumps[0], 1);
// Multiplicate the flux jumps for the correction
// function
for (i = 0; i < nquad0; ++i)
{
for (j = 0; j < nquad1; ++j)
{
cnt = i + j*nquad0;
divCFluxE0[cnt] =
-fluxJumps[i] * m_dGL_xi2[n][j];
}
}
break;
case 1:
// Extract the edge values of transformed flux-x on
// edge e and order them accordingly to the order of
// the trace space
fields[0]->GetExp(n)->GetEdgePhysVals(
e, elmtToTrace[n][e],
fluxX1 + phys_offset,
auxArray1 = fluxN_D);
// Extract the physical Rieamann flux at each edge
Vmath::Vcopy(nEdgePts,
&numericalFlux[trace_offset], 1,
&fluxN[0], 1);
// Check the ordering of vectors
if (fields[0]->GetExp(n)->GetEorient(e) ==
StdRegions::eBackwards)
{
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN, 1,
auxArray2 = fluxN, 1);
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN_D, 1,
auxArray2 = fluxN_D, 1);
}
// Transform Riemann Fluxes in the standard element
for (i = 0; i < nquad1; ++i)
{
// Multiply Riemann Flux by Q factors
fluxN_R[i] = (m_Q2D_e1[n][i]) * fluxN[i];
}
fac = fields[0]->GetExp(n)->EdgeNormalNegated(e) ?
-1.0 : 1.0;
for (i = 0; i < nEdgePts; ++i)
{
if (m_traceNormals[0][trace_offset+i]
!= fac*normals[0][i] ||
m_traceNormals[1][trace_offset+i]
!= fac*normals[1][i])
{
fluxN_R[i] = -fluxN_R[i];
}
}
// Subtract to the Riemann flux the discontinuous
// flux
Vmath::Vsub(nEdgePts,
&fluxN_R[0], 1,
&fluxN_D[0], 1, &fluxJumps[0], 1);
// Multiplicate the flux jumps for the correction
// function
for (i = 0; i < nquad1; ++i)
{
for (j = 0; j < nquad0; ++j)
{
cnt = (nquad0)*i + j;
divCFluxE1[cnt] =
fluxJumps[i] * m_dGR_xi1[n][j];
}
}
break;
case 2:
// Extract the edge values of transformed flux-y on
// edge e and order them accordingly to the order of
// the trace space
fields[0]->GetExp(n)->GetEdgePhysVals(
e, elmtToTrace[n][e],
fluxX2 + phys_offset,
auxArray1 = fluxN_D);
// Extract the physical Rieamann flux at each edge
Vmath::Vcopy(nEdgePts,
&numericalFlux[trace_offset], 1,
&fluxN[0], 1);
// Check the ordering of vectors
if (fields[0]->GetExp(n)->GetEorient(e) ==
StdRegions::eBackwards)
{
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN, 1,
auxArray2 = fluxN, 1);
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN_D, 1,
auxArray2 = fluxN_D, 1);
}
// Transform Riemann Fluxes in the standard element
for (i = 0; i < nquad0; ++i)
{
// Multiply Riemann Flux by Q factors
fluxN_R[i] = (m_Q2D_e2[n][i]) * fluxN[i];
}
fac = fields[0]->GetExp(n)->EdgeNormalNegated(e) ?
-1.0 : 1.0;
for (i = 0; i < nEdgePts; ++i)
{
if (m_traceNormals[0][trace_offset+i]
!= fac*normals[0][i] ||
m_traceNormals[1][trace_offset+i]
!= fac*normals[1][i])
{
fluxN_R[i] = -fluxN_R[i];
}
}
// Subtract to the Riemann flux the discontinuous
// flux
Vmath::Vsub(nEdgePts,
&fluxN_R[0], 1,
&fluxN_D[0], 1, &fluxJumps[0], 1);
// Multiplicate the flux jumps for the correction
// function
for (i = 0; i < nquad0; ++i)
{
for (j = 0; j < nquad1; ++j)
{
cnt = (nquad0 - 1) + j*nquad0 - i;
divCFluxE2[cnt] =
fluxJumps[i] * m_dGR_xi2[n][j];
}
}
break;
case 3:
// Extract the edge values of transformed flux-x on
// edge e and order them accordingly to the order of
// the trace space
fields[0]->GetExp(n)->GetEdgePhysVals(
e, elmtToTrace[n][e],
fluxX1 + phys_offset,
auxArray1 = fluxN_D);
Vmath::Neg (nEdgePts, fluxN_D, 1);
// Extract the physical Rieamann flux at each edge
Vmath::Vcopy(nEdgePts,
&numericalFlux[trace_offset], 1,
&fluxN[0], 1);
// Check the ordering of vectors
if (fields[0]->GetExp(n)->GetEorient(e) ==
StdRegions::eBackwards)
{
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN, 1,
auxArray2 = fluxN, 1);
Vmath::Reverse(nEdgePts,
auxArray1 = fluxN_D, 1,
auxArray2 = fluxN_D, 1);
}
// Transform Riemann Fluxes in the standard element
for (i = 0; i < nquad1; ++i)
{
// Multiply Riemann Flux by Q factors
fluxN_R[i] = (m_Q2D_e3[n][i]) * fluxN[i];
}
fac = fields[0]->GetExp(n)->EdgeNormalNegated(e) ?
-1.0 : 1.0;
for (i = 0; i < nEdgePts; ++i)
{
if (m_traceNormals[0][trace_offset+i]
!= fac*normals[0][i] ||
m_traceNormals[1][trace_offset+i]
!= fac*normals[1][i])
{
fluxN_R[i] = -fluxN_R[i];
}
}
// Subtract to the Riemann flux the discontinuous
// flux
Vmath::Vsub(nEdgePts,
&fluxN_R[0], 1,
&fluxN_D[0], 1, &fluxJumps[0], 1);
// Multiplicate the flux jumps for the correction
// function
for (i = 0; i < nquad1; ++i)
{
for (j = 0; j < nquad0; ++j)
{
cnt = (nquad0*nquad1 - nquad0) + j
- i*nquad0;
divCFluxE3[cnt] =
-fluxJumps[i] * m_dGL_xi1[n][j];
}
}
break;
default:
ASSERTL0(false,"edge value (< 3) is out of range");
break;
}
}
// Sum each edge contribution
Vmath::Vadd(nLocalSolutionPts, &divCFluxE0[0], 1,
&divCFluxE1[0], 1, &divCFlux[phys_offset], 1);
Vmath::Vadd(nLocalSolutionPts, &divCFlux[phys_offset], 1,
&divCFluxE2[0], 1, &divCFlux[phys_offset], 1);
Vmath::Vadd(nLocalSolutionPts, &divCFlux[phys_offset], 1,
&divCFluxE3[0], 1, &divCFlux[phys_offset], 1);
}
}
void Nektar::SolverUtils::AdvectionFR::v_DivCFlux_3D ( const int  nConvectiveFields,
const Array< OneD, MultiRegions::ExpListSharedPtr > &  fields,
const Array< OneD, const NekDouble > &  fluxX1,
const Array< OneD, const NekDouble > &  fluxX2,
const Array< OneD, const NekDouble > &  fluxX3,
const Array< OneD, const NekDouble > &  numericalFlux,
Array< OneD, NekDouble > &  divCFlux 
)
protectedvirtual

Compute the divergence of the corrective flux for 3D problems.

Parameters
nConvectiveFieldsNumber of fields.
fieldsPointer to fields.
fluxX1X1-volumetric flux in physical space.
fluxX2X2-volumetric flux in physical space.
fluxX3X3-volumetric flux in physical space.
numericalFluxInterface flux in physical space.
divCFluxDivergence of the corrective flux.
Todo:
: To be implemented. Switch on shapes eventually here.

Definition at line 1669 of file AdvectionFR.cpp.

{
}
void Nektar::SolverUtils::AdvectionFR::v_InitObject ( LibUtilities::SessionReaderSharedPtr  pSession,
Array< OneD, MultiRegions::ExpListSharedPtr >  pFields 
)
protectedvirtual

Initiliase AdvectionFR objects and store them before starting the time-stepping.

This routine calls the virtual functions v_SetupMetrics and v_SetupCFunctions to initialise the objects needed by AdvectionFR.

Parameters
pSessionPointer to session reader.
pFieldsPointer to fields.

Reimplemented from Nektar::SolverUtils::Advection.

Definition at line 89 of file AdvectionFR.cpp.

References v_SetupCFunctions(), and v_SetupMetrics().

{
Advection::v_InitObject(pSession, pFields);
v_SetupMetrics (pSession, pFields);
v_SetupCFunctions (pSession, pFields);
}
void Nektar::SolverUtils::AdvectionFR::v_SetupCFunctions ( LibUtilities::SessionReaderSharedPtr  pSession,
Array< OneD, MultiRegions::ExpListSharedPtr >  pFields 
)
protectedvirtual

Setup the derivatives of the correction functions. For more details see J Sci Comput (2011) 47: 50–72.

This routine calls 3 different bases: #eDG_DG_Left - #eDG_DG_Left which recovers a nodal DG scheme, #eDG_SD_Left - #eDG_SD_Left which recovers the SD scheme, #eDG_HU_Left - #eDG_HU_Left which recovers the Huynh scheme. The values of the derivatives of the correction function are then stored into global variables and reused into the virtual functions v_DivCFlux_1D, v_DivCFlux_2D, v_DivCFlux_3D to compute the the divergence of the correction flux for 1D, 2D or 3D problems.

Parameters
pSessionPointer to session reader.
pFieldsPointer to fields.

Definition at line 268 of file AdvectionFR.cpp.

References ASSERTL0, Polylib::jacobd(), m_advType, m_dGL_xi1, m_dGL_xi2, m_dGL_xi3, m_dGR_xi1, m_dGR_xi2, and m_dGR_xi3.

Referenced by v_InitObject().

{
int i, n;
NekDouble c0, c1, c2;
int nquad0, nquad1, nquad2;
int nmodes0, nmodes1, nmodes2;
Array<OneD, LibUtilities::BasisSharedPtr> base;
int nElements = pFields[0]->GetExpSize();
int nDimensions = pFields[0]->GetCoordim(0);
switch (nDimensions)
{
case 1:
{
m_dGL_xi1 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGR_xi1 = Array<OneD, Array<OneD, NekDouble> >(nElements);
for (n = 0; n < nElements; ++n)
{
base = pFields[0]->GetExp(n)->GetBase();
nquad0 = base[0]->GetNumPoints();
nmodes0 = base[0]->GetNumModes();
Array<OneD, const NekDouble> z0;
Array<OneD, const NekDouble> w0;
base[0]->GetZW(z0, w0);
m_dGL_xi1[n] = Array<OneD, NekDouble>(nquad0);
m_dGR_xi1[n] = Array<OneD, NekDouble>(nquad0);
// Auxiliary vectors to build up the auxiliary
// derivatives of the Legendre polynomials
Array<OneD,NekDouble> dLp0 (nquad0, 0.0);
Array<OneD,NekDouble> dLpp0(nquad0, 0.0);
Array<OneD,NekDouble> dLpm0(nquad0, 0.0);
// Degree of the correction functions
int p0 = nmodes0 - 1;
// Function sign to compute left correction function
NekDouble sign0 = pow(-1.0, p0);
// Factorial factor to build the scheme
NekDouble ap0 = boost::math::tgamma(2 * p0 + 1)
/ (pow(2.0, p0)
* boost::math::tgamma(p0 + 1)
* boost::math::tgamma(p0 + 1));
// Scalar parameter which recovers the FR schemes
if (m_advType == "FRDG")
{
c0 = 0.0;
}
else if (m_advType == "FRSD")
{
c0 = 2.0 * p0 / ((2.0 * p0 + 1.0) * (p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
}
else if (m_advType == "FRHU")
{
c0 = 2.0 * (p0 + 1.0) / ((2.0 * p0 + 1.0) * p0
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
}
else if (m_advType == "FRcmin")
{
c0 = -2.0 / ((2.0 * p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
}
else if (m_advType == "FRcinf")
{
c0 = 10000000000000000.0;
}
NekDouble etap0 = 0.5 * c0 * (2.0 * p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1));
NekDouble overeta0 = 1.0 / (1.0 + etap0);
// Derivative of the Legendre polynomials
// dLp = derivative of the Legendre polynomial of order p
// dLpp = derivative of the Legendre polynomial of order p+1
// dLpm = derivative of the Legendre polynomial of order p-1
Polylib::jacobd(nquad0, z0.data(), &(dLp0[0]), p0, 0.0, 0.0);
Polylib::jacobd(nquad0, z0.data(), &(dLpp0[0]), p0+1, 0.0, 0.0);
Polylib::jacobd(nquad0, z0.data(), &(dLpm0[0]), p0-1, 0.0, 0.0);
// Building the DG_c_Left
for(i = 0; i < nquad0; ++i)
{
m_dGL_xi1[n][i] = etap0 * dLpm0[i];
m_dGL_xi1[n][i] += dLpp0[i];
m_dGL_xi1[n][i] *= overeta0;
m_dGL_xi1[n][i] = dLp0[i] - m_dGL_xi1[n][i];
m_dGL_xi1[n][i] = 0.5 * sign0 * m_dGL_xi1[n][i];
}
// Building the DG_c_Right
for(i = 0; i < nquad0; ++i)
{
m_dGR_xi1[n][i] = etap0 * dLpm0[i];
m_dGR_xi1[n][i] += dLpp0[i];
m_dGR_xi1[n][i] *= overeta0;
m_dGR_xi1[n][i] += dLp0[i];
m_dGR_xi1[n][i] = 0.5 * m_dGR_xi1[n][i];
}
}
break;
}
case 2:
{
LibUtilities::BasisSharedPtr BasisFR_Left0;
LibUtilities::BasisSharedPtr BasisFR_Right0;
LibUtilities::BasisSharedPtr BasisFR_Left1;
LibUtilities::BasisSharedPtr BasisFR_Right1;
m_dGL_xi1 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGR_xi1 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGL_xi2 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGR_xi2 = Array<OneD, Array<OneD, NekDouble> >(nElements);
for (n = 0; n < nElements; ++n)
{
base = pFields[0]->GetExp(n)->GetBase();
nquad0 = base[0]->GetNumPoints();
nquad1 = base[1]->GetNumPoints();
nmodes0 = base[0]->GetNumModes();
nmodes1 = base[1]->GetNumModes();
Array<OneD, const NekDouble> z0;
Array<OneD, const NekDouble> w0;
Array<OneD, const NekDouble> z1;
Array<OneD, const NekDouble> w1;
base[0]->GetZW(z0, w0);
base[1]->GetZW(z1, w1);
m_dGL_xi1[n] = Array<OneD, NekDouble>(nquad0);
m_dGR_xi1[n] = Array<OneD, NekDouble>(nquad0);
m_dGL_xi2[n] = Array<OneD, NekDouble>(nquad1);
m_dGR_xi2[n] = Array<OneD, NekDouble>(nquad1);
// Auxiliary vectors to build up the auxiliary
// derivatives of the Legendre polynomials
Array<OneD,NekDouble> dLp0 (nquad0, 0.0);
Array<OneD,NekDouble> dLpp0 (nquad0, 0.0);
Array<OneD,NekDouble> dLpm0 (nquad0, 0.0);
Array<OneD,NekDouble> dLp1 (nquad1, 0.0);
Array<OneD,NekDouble> dLpp1 (nquad1, 0.0);
Array<OneD,NekDouble> dLpm1 (nquad1, 0.0);
// Degree of the correction functions
int p0 = nmodes0 - 1;
int p1 = nmodes1 - 1;
// Function sign to compute left correction function
NekDouble sign0 = pow(-1.0, p0);
NekDouble sign1 = pow(-1.0, p1);
// Factorial factor to build the scheme
NekDouble ap0 = boost::math::tgamma(2 * p0 + 1)
/ (pow(2.0, p0)
* boost::math::tgamma(p0 + 1)
* boost::math::tgamma(p0 + 1));
NekDouble ap1 = boost::math::tgamma(2 * p1 + 1)
/ (pow(2.0, p1)
* boost::math::tgamma(p1 + 1)
* boost::math::tgamma(p1 + 1));
// Scalar parameter which recovers the FR schemes
if (m_advType == "FRDG")
{
c0 = 0.0;
c1 = 0.0;
}
else if (m_advType == "FRSD")
{
c0 = 2.0 * p0 / ((2.0 * p0 + 1.0) * (p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
c1 = 2.0 * p1 / ((2.0 * p1 + 1.0) * (p1 + 1.0)
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1)));
}
else if (m_advType == "FRHU")
{
c0 = 2.0 * (p0 + 1.0) / ((2.0 * p0 + 1.0) * p0
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
c1 = 2.0 * (p1 + 1.0) / ((2.0 * p1 + 1.0) * p1
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1)));
}
else if (m_advType == "FRcmin")
{
c0 = -2.0 / ((2.0 * p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
c1 = -2.0 / ((2.0 * p1 + 1.0)
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1)));
}
else if (m_advType == "FRcinf")
{
c0 = 10000000000000000.0;
c1 = 10000000000000000.0;
}
NekDouble etap0 = 0.5 * c0 * (2.0 * p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1));
NekDouble etap1 = 0.5 * c1 * (2.0 * p1 + 1.0)
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1));
NekDouble overeta0 = 1.0 / (1.0 + etap0);
NekDouble overeta1 = 1.0 / (1.0 + etap1);
// Derivative of the Legendre polynomials
// dLp = derivative of the Legendre polynomial of order p
// dLpp = derivative of the Legendre polynomial of order p+1
// dLpm = derivative of the Legendre polynomial of order p-1
Polylib::jacobd(nquad0, z0.data(), &(dLp0[0]), p0, 0.0, 0.0);
Polylib::jacobd(nquad0, z0.data(), &(dLpp0[0]), p0+1, 0.0, 0.0);
Polylib::jacobd(nquad0, z0.data(), &(dLpm0[0]), p0-1, 0.0, 0.0);
Polylib::jacobd(nquad1, z1.data(), &(dLp1[0]), p1, 0.0, 0.0);
Polylib::jacobd(nquad1, z1.data(), &(dLpp1[0]), p1+1, 0.0, 0.0);
Polylib::jacobd(nquad1, z1.data(), &(dLpm1[0]), p1-1, 0.0, 0.0);
// Building the DG_c_Left
for(i = 0; i < nquad0; ++i)
{
m_dGL_xi1[n][i] = etap0 * dLpm0[i];
m_dGL_xi1[n][i] += dLpp0[i];
m_dGL_xi1[n][i] *= overeta0;
m_dGL_xi1[n][i] = dLp0[i] - m_dGL_xi1[n][i];
m_dGL_xi1[n][i] = 0.5 * sign0 * m_dGL_xi1[n][i];
}
// Building the DG_c_Left
for(i = 0; i < nquad1; ++i)
{
m_dGL_xi2[n][i] = etap1 * dLpm1[i];
m_dGL_xi2[n][i] += dLpp1[i];
m_dGL_xi2[n][i] *= overeta1;
m_dGL_xi2[n][i] = dLp1[i] - m_dGL_xi2[n][i];
m_dGL_xi2[n][i] = 0.5 * sign1 * m_dGL_xi2[n][i];
}
// Building the DG_c_Right
for(i = 0; i < nquad0; ++i)
{
m_dGR_xi1[n][i] = etap0 * dLpm0[i];
m_dGR_xi1[n][i] += dLpp0[i];
m_dGR_xi1[n][i] *= overeta0;
m_dGR_xi1[n][i] += dLp0[i];
m_dGR_xi1[n][i] = 0.5 * m_dGR_xi1[n][i];
}
// Building the DG_c_Right
for(i = 0; i < nquad1; ++i)
{
m_dGR_xi2[n][i] = etap1 * dLpm1[i];
m_dGR_xi2[n][i] += dLpp1[i];
m_dGR_xi2[n][i] *= overeta1;
m_dGR_xi2[n][i] += dLp1[i];
m_dGR_xi2[n][i] = 0.5 * m_dGR_xi2[n][i];
}
}
break;
}
case 3:
{
m_dGL_xi1 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGR_xi1 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGL_xi2 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGR_xi2 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGL_xi3 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_dGR_xi3 = Array<OneD, Array<OneD, NekDouble> >(nElements);
for (n = 0; n < nElements; ++n)
{
base = pFields[0]->GetExp(n)->GetBase();
nquad0 = base[0]->GetNumPoints();
nquad1 = base[1]->GetNumPoints();
nquad2 = base[2]->GetNumPoints();
nmodes0 = base[0]->GetNumModes();
nmodes1 = base[1]->GetNumModes();
nmodes2 = base[2]->GetNumModes();
Array<OneD, const NekDouble> z0;
Array<OneD, const NekDouble> w0;
Array<OneD, const NekDouble> z1;
Array<OneD, const NekDouble> w1;
Array<OneD, const NekDouble> z2;
Array<OneD, const NekDouble> w2;
base[0]->GetZW(z0, w0);
base[1]->GetZW(z1, w1);
base[1]->GetZW(z2, w2);
m_dGL_xi1[n] = Array<OneD, NekDouble>(nquad0);
m_dGR_xi1[n] = Array<OneD, NekDouble>(nquad0);
m_dGL_xi2[n] = Array<OneD, NekDouble>(nquad1);
m_dGR_xi2[n] = Array<OneD, NekDouble>(nquad1);
m_dGL_xi3[n] = Array<OneD, NekDouble>(nquad2);
m_dGR_xi3[n] = Array<OneD, NekDouble>(nquad2);
// Auxiliary vectors to build up the auxiliary
// derivatives of the Legendre polynomials
Array<OneD,NekDouble> dLp0 (nquad0, 0.0);
Array<OneD,NekDouble> dLpp0 (nquad0, 0.0);
Array<OneD,NekDouble> dLpm0 (nquad0, 0.0);
Array<OneD,NekDouble> dLp1 (nquad1, 0.0);
Array<OneD,NekDouble> dLpp1 (nquad1, 0.0);
Array<OneD,NekDouble> dLpm1 (nquad1, 0.0);
Array<OneD,NekDouble> dLp2 (nquad2, 0.0);
Array<OneD,NekDouble> dLpp2 (nquad2, 0.0);
Array<OneD,NekDouble> dLpm2 (nquad2, 0.0);
// Degree of the correction functions
int p0 = nmodes0 - 1;
int p1 = nmodes1 - 1;
int p2 = nmodes2 - 1;
// Function sign to compute left correction function
NekDouble sign0 = pow(-1.0, p0);
NekDouble sign1 = pow(-1.0, p1);
// Factorial factor to build the scheme
NekDouble ap0 = boost::math::tgamma(2 * p0 + 1)
/ (pow(2.0, p0)
* boost::math::tgamma(p0 + 1)
* boost::math::tgamma(p0 + 1));
// Factorial factor to build the scheme
NekDouble ap1 = boost::math::tgamma(2 * p1 + 1)
/ (pow(2.0, p1)
* boost::math::tgamma(p1 + 1)
* boost::math::tgamma(p1 + 1));
// Factorial factor to build the scheme
NekDouble ap2 = boost::math::tgamma(2 * p2 + 1)
/ (pow(2.0, p2)
* boost::math::tgamma(p2 + 1)
* boost::math::tgamma(p2 + 1));
// Scalar parameter which recovers the FR schemes
if (m_advType == "FRDG")
{
c0 = 0.0;
c1 = 0.0;
c2 = 0.0;
}
else if (m_advType == "FRSD")
{
c0 = 2.0 * p0 / ((2.0 * p0 + 1.0) * (p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
c1 = 2.0 * p1 / ((2.0 * p1 + 1.0) * (p1 + 1.0)
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1)));
c2 = 2.0 * p2 / ((2.0 * p2 + 1.0) * (p2 + 1.0)
* (ap2 * boost::math::tgamma(p2 + 1))
* (ap2 * boost::math::tgamma(p2 + 1)));
}
else if (m_advType == "FRHU")
{
c0 = 2.0 * (p0 + 1.0) / ((2.0 * p0 + 1.0) * p0
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
c1 = 2.0 * (p1 + 1.0) / ((2.0 * p1 + 1.0) * p1
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1)));
c2 = 2.0 * (p2 + 1.0) / ((2.0 * p2 + 1.0) * p2
* (ap2 * boost::math::tgamma(p2 + 1))
* (ap2 * boost::math::tgamma(p2 + 1)));
}
else if (m_advType == "FRcmin")
{
c0 = -2.0 / ((2.0 * p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1)));
c1 = -2.0 / ((2.0 * p1 + 1.0)
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1)));
c2 = -2.0 / ((2.0 * p2 + 1.0)
* (ap2 * boost::math::tgamma(p2 + 1))
* (ap2 * boost::math::tgamma(p2 + 1)));
}
else if (m_advType == "FRcinf")
{
c0 = 10000000000000000.0;
c1 = 10000000000000000.0;
c2 = 10000000000000000.0;
}
NekDouble etap0 = 0.5 * c0 * (2.0 * p0 + 1.0)
* (ap0 * boost::math::tgamma(p0 + 1))
* (ap0 * boost::math::tgamma(p0 + 1));
NekDouble etap1 = 0.5 * c1 * (2.0 * p1 + 1.0)
* (ap1 * boost::math::tgamma(p1 + 1))
* (ap1 * boost::math::tgamma(p1 + 1));
NekDouble etap2 = 0.5 * c2 * (2.0 * p2 + 1.0)
* (ap2 * boost::math::tgamma(p2 + 1))
* (ap2 * boost::math::tgamma(p2 + 1));
NekDouble overeta0 = 1.0 / (1.0 + etap0);
NekDouble overeta1 = 1.0 / (1.0 + etap1);
NekDouble overeta2 = 1.0 / (1.0 + etap2);
// Derivative of the Legendre polynomials
// dLp = derivative of the Legendre polynomial of order p
// dLpp = derivative of the Legendre polynomial of order p+1
// dLpm = derivative of the Legendre polynomial of order p-1
Polylib::jacobd(nquad0, z0.data(), &(dLp0[0]), p0, 0.0, 0.0);
Polylib::jacobd(nquad0, z0.data(), &(dLpp0[0]), p0+1, 0.0, 0.0);
Polylib::jacobd(nquad0, z0.data(), &(dLpm0[0]), p0-1, 0.0, 0.0);
Polylib::jacobd(nquad1, z1.data(), &(dLp1[0]), p1, 0.0, 0.0);
Polylib::jacobd(nquad1, z1.data(), &(dLpp1[0]), p1+1, 0.0, 0.0);
Polylib::jacobd(nquad1, z1.data(), &(dLpm1[0]), p1-1, 0.0, 0.0);
Polylib::jacobd(nquad2, z2.data(), &(dLp2[0]), p2, 0.0, 0.0);
Polylib::jacobd(nquad2, z2.data(), &(dLpp2[0]), p2+1, 0.0, 0.0);
Polylib::jacobd(nquad2, z2.data(), &(dLpm2[0]), p2-1, 0.0, 0.0);
// Building the DG_c_Left
for(i = 0; i < nquad0; ++i)
{
m_dGL_xi1[n][i] = etap0 * dLpm0[i];
m_dGL_xi1[n][i] += dLpp0[i];
m_dGL_xi1[n][i] *= overeta0;
m_dGL_xi1[n][i] = dLp0[i] - m_dGL_xi1[n][i];
m_dGL_xi1[n][i] = 0.5 * sign0 * m_dGL_xi1[n][i];
}
// Building the DG_c_Left
for(i = 0; i < nquad1; ++i)
{
m_dGL_xi2[n][i] = etap1 * dLpm1[i];
m_dGL_xi2[n][i] += dLpp1[i];
m_dGL_xi2[n][i] *= overeta1;
m_dGL_xi2[n][i] = dLp1[i] - m_dGL_xi2[n][i];
m_dGL_xi2[n][i] = 0.5 * sign1 * m_dGL_xi2[n][i];
}
// Building the DG_c_Left
for(i = 0; i < nquad2; ++i)
{
m_dGL_xi3[n][i] = etap2 * dLpm2[i];
m_dGL_xi3[n][i] += dLpp2[i];
m_dGL_xi3[n][i] *= overeta2;
m_dGL_xi3[n][i] = dLp2[i] - m_dGL_xi3[n][i];
m_dGL_xi3[n][i] = 0.5 * sign1 * m_dGL_xi3[n][i];
}
// Building the DG_c_Right
for(i = 0; i < nquad0; ++i)
{
m_dGR_xi1[n][i] = etap0 * dLpm0[i];
m_dGR_xi1[n][i] += dLpp0[i];
m_dGR_xi1[n][i] *= overeta0;
m_dGR_xi1[n][i] += dLp0[i];
m_dGR_xi1[n][i] = 0.5 * m_dGR_xi1[n][i];
}
// Building the DG_c_Right
for(i = 0; i < nquad1; ++i)
{
m_dGR_xi2[n][i] = etap1 * dLpm1[i];
m_dGR_xi2[n][i] += dLpp1[i];
m_dGR_xi2[n][i] *= overeta1;
m_dGR_xi2[n][i] += dLp1[i];
m_dGR_xi2[n][i] = 0.5 * m_dGR_xi2[n][i];
}
// Building the DG_c_Right
for(i = 0; i < nquad2; ++i)
{
m_dGR_xi3[n][i] = etap2 * dLpm2[i];
m_dGR_xi3[n][i] += dLpp2[i];
m_dGR_xi3[n][i] *= overeta2;
m_dGR_xi3[n][i] += dLp2[i];
m_dGR_xi3[n][i] = 0.5 * m_dGR_xi3[n][i];
}
}
break;
}
default:
{
ASSERTL0(false,"Expansion dimension not recognised");
break;
}
}
}
void Nektar::SolverUtils::AdvectionFR::v_SetupMetrics ( LibUtilities::SessionReaderSharedPtr  pSession,
Array< OneD, MultiRegions::ExpListSharedPtr >  pFields 
)
protectedvirtual

Setup the metric terms to compute the contravariant fluxes. (i.e. this special metric terms transform the fluxes at the interfaces of each element from the physical space to the standard space).

This routine calls the function #GetEdgeQFactors to compute and store the metric factors following an anticlockwise conventions along the edges/faces of each element. Note: for 1D problem the transformation is not needed.

Parameters
pSessionPointer to session reader.
pFieldsPointer to fields.
Todo:
Add the metric terms for 3D Hexahedra.

Definition at line 114 of file AdvectionFR.cpp.

References ASSERTL0, Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetMetricInfo(), m_gmat, m_jac, m_Q2D_e0, m_Q2D_e1, m_Q2D_e2, m_Q2D_e3, and m_traceNormals.

Referenced by v_InitObject().

{
int i, n;
int nquad0, nquad1;
int phys_offset;
int nLocalSolutionPts;
int nElements = pFields[0]->GetExpSize();
int nDimensions = pFields[0]->GetCoordim(0);
int nSolutionPts = pFields[0]->GetTotPoints();
int nTracePts = pFields[0]->GetTrace()->GetTotPoints();
Array<TwoD, const NekDouble> gmat;
Array<OneD, const NekDouble> jac;
m_jac = Array<OneD, NekDouble>(nSolutionPts);
Array<OneD, NekDouble> auxArray1;
Array<OneD, LibUtilities::BasisSharedPtr> base;
LibUtilities::PointsKeyVector ptsKeys;
switch (nDimensions)
{
case 1:
{
for (n = 0; n < nElements; ++n)
{
ptsKeys = pFields[0]->GetExp(n)->GetPointsKeys();
nLocalSolutionPts = pFields[0]->GetExp(n)->GetTotPoints();
phys_offset = pFields[0]->GetPhys_Offset(n);
jac = pFields[0]->GetExp(n)
->as<LocalRegions::Expansion1D>()->GetGeom1D()
->GetMetricInfo()->GetJac(ptsKeys);
for (i = 0; i < nLocalSolutionPts; ++i)
{
m_jac[i+phys_offset] = jac[0];
}
}
break;
}
case 2:
{
m_gmat = Array<OneD, Array<OneD, NekDouble> >(4);
m_gmat[0] = Array<OneD, NekDouble>(nSolutionPts);
m_gmat[1] = Array<OneD, NekDouble>(nSolutionPts);
m_gmat[2] = Array<OneD, NekDouble>(nSolutionPts);
m_gmat[3] = Array<OneD, NekDouble>(nSolutionPts);
m_Q2D_e0 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_Q2D_e1 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_Q2D_e2 = Array<OneD, Array<OneD, NekDouble> >(nElements);
m_Q2D_e3 = Array<OneD, Array<OneD, NekDouble> >(nElements);
LibUtilities::PointsKeyVector ptsKeys;
for (n = 0; n < nElements; ++n)
{
base = pFields[0]->GetExp(n)->GetBase();
nquad0 = base[0]->GetNumPoints();
nquad1 = base[1]->GetNumPoints();
m_Q2D_e0[n] = Array<OneD, NekDouble>(nquad0);
m_Q2D_e1[n] = Array<OneD, NekDouble>(nquad1);
m_Q2D_e2[n] = Array<OneD, NekDouble>(nquad0);
m_Q2D_e3[n] = Array<OneD, NekDouble>(nquad1);
// Extract the Q factors at each edge point
pFields[0]->GetExp(n)->GetEdgeQFactors(
0, auxArray1 = m_Q2D_e0[n]);
pFields[0]->GetExp(n)->GetEdgeQFactors(
1, auxArray1 = m_Q2D_e1[n]);
pFields[0]->GetExp(n)->GetEdgeQFactors(
2, auxArray1 = m_Q2D_e2[n]);
pFields[0]->GetExp(n)->GetEdgeQFactors(
3, auxArray1 = m_Q2D_e3[n]);
ptsKeys = pFields[0]->GetExp(n)->GetPointsKeys();
nLocalSolutionPts = pFields[0]->GetExp(n)->GetTotPoints();
phys_offset = pFields[0]->GetPhys_Offset(n);
jac = pFields[0]->GetExp(n)
->as<LocalRegions::Expansion2D>()->GetGeom2D()
->GetMetricInfo()->GetJac(ptsKeys);
gmat = pFields[0]->GetExp(n)
->as<LocalRegions::Expansion2D>()->GetGeom2D()
->GetMetricInfo()->GetDerivFactors(ptsKeys);
if (pFields[0]->GetExp(n)
->as<LocalRegions::Expansion2D>()->GetGeom2D()
->GetMetricInfo()->GetGtype()
== SpatialDomains::eDeformed)
{
for (i = 0; i < nLocalSolutionPts; ++i)
{
m_jac[i+phys_offset] = jac[i];
m_gmat[0][i+phys_offset] = gmat[0][i];
m_gmat[1][i+phys_offset] = gmat[1][i];
m_gmat[2][i+phys_offset] = gmat[2][i];
m_gmat[3][i+phys_offset] = gmat[3][i];
}
}
else
{
for (i = 0; i < nLocalSolutionPts; ++i)
{
m_jac[i+phys_offset] = jac[0];
m_gmat[0][i+phys_offset] = gmat[0][0];
m_gmat[1][i+phys_offset] = gmat[1][0];
m_gmat[2][i+phys_offset] = gmat[2][0];
m_gmat[3][i+phys_offset] = gmat[3][0];
}
}
}
m_traceNormals = Array<OneD, Array<OneD, NekDouble> >(
nDimensions);
for(i = 0; i < nDimensions; ++i)
{
m_traceNormals[i] = Array<OneD, NekDouble> (nTracePts);
}
pFields[0]->GetTrace()->GetNormals(m_traceNormals);
break;
}
case 3:
{
ASSERTL0(false,"3DFR Metric terms not implemented yet");
break;
}
default:
{
ASSERTL0(false, "Expansion dimension not recognised");
break;
}
}
}

Member Data Documentation

std::string Nektar::SolverUtils::AdvectionFR::m_advType
protected

Definition at line 79 of file AdvectionFR.h.

Referenced by v_SetupCFunctions().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_dGL_xi1

Definition at line 65 of file AdvectionFR.h.

Referenced by v_DivCFlux_1D(), v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupCFunctions().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_dGL_xi2

Definition at line 67 of file AdvectionFR.h.

Referenced by v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupCFunctions().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_dGL_xi3

Definition at line 69 of file AdvectionFR.h.

Referenced by v_SetupCFunctions().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_dGR_xi1

Definition at line 66 of file AdvectionFR.h.

Referenced by v_DivCFlux_1D(), v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupCFunctions().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_dGR_xi2

Definition at line 68 of file AdvectionFR.h.

Referenced by v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupCFunctions().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_dGR_xi3

Definition at line 70 of file AdvectionFR.h.

Referenced by v_SetupCFunctions().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_gmat

Definition at line 58 of file AdvectionFR.h.

Referenced by v_Advect(), and v_SetupMetrics().

DNekMatSharedPtr Nektar::SolverUtils::AdvectionFR::m_Ixm

Definition at line 71 of file AdvectionFR.h.

DNekMatSharedPtr Nektar::SolverUtils::AdvectionFR::m_Ixp

Definition at line 72 of file AdvectionFR.h.

Array<OneD, NekDouble> Nektar::SolverUtils::AdvectionFR::m_jac

Definition at line 57 of file AdvectionFR.h.

Referenced by v_Advect(), and v_SetupMetrics().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_Q2D_e0

Definition at line 60 of file AdvectionFR.h.

Referenced by v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupMetrics().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_Q2D_e1

Definition at line 61 of file AdvectionFR.h.

Referenced by v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupMetrics().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_Q2D_e2

Definition at line 62 of file AdvectionFR.h.

Referenced by v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupMetrics().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_Q2D_e3

Definition at line 63 of file AdvectionFR.h.

Referenced by v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupMetrics().

Array<OneD, Array<OneD, NekDouble> > Nektar::SolverUtils::AdvectionFR::m_traceNormals
protected

Definition at line 77 of file AdvectionFR.h.

Referenced by v_DivCFlux_2D(), v_DivCFlux_2D_Gauss(), and v_SetupMetrics().

std::string Nektar::SolverUtils::AdvectionFR::type
static
Initial value:
{
GetAdvectionFactory().RegisterCreatorFunction(
"FRDG", AdvectionFR::create),
GetAdvectionFactory().RegisterCreatorFunction(
"FRSD", AdvectionFR::create),
GetAdvectionFactory().RegisterCreatorFunction(
"FRHU", AdvectionFR::create),
GetAdvectionFactory().RegisterCreatorFunction(
"FRcmin", AdvectionFR::create),
GetAdvectionFactory().RegisterCreatorFunction(
"FRcinf", AdvectionFR::create)}

Definition at line 55 of file AdvectionFR.h.

Generated on Sun Mar 15 2015 00:12:01 for Nektar++ by   doxygen 1.8.1.2