|
Nektar++
|
|
Nektar++
|
Namespaces | |
| namespace | StdHexData |
| namespace | StdPrismData |
| namespace | StdPyrData |
| namespace | StdQuadData |
| namespace | StdSegData |
| namespace | StdTetData |
| namespace | StdTriData |
Typedefs | |
| typedef std::map< std::string, std::string > | FieldMetaDataMap |
| typedef boost::shared_ptr < FieldDefinitions > | FieldDefinitionsSharedPtr |
| typedef boost::shared_ptr < FieldIO > | FieldIOSharedPtr |
| typedef boost::shared_ptr < SessionReader > | SessionReaderSharedPtr |
| typedef std::map< int, std::vector< unsigned int > > | CompositeOrdering |
| typedef std::map< int, std::vector< unsigned int > > | BndRegionOrdering |
| typedef LibUtilities::NekFactory < std::string, MeshPartition, const SessionReaderSharedPtr & > | MeshPartitionFactory |
| Datatype of the NekFactory used to instantiate classes derived from the EquationSystem class. | |
| typedef boost::shared_ptr < MeshPartition > | MeshPartitionSharedPtr |
| typedef std::map< std::string, std::string > | SolverInfoMap |
| typedef std::map< std::string, NekDouble > | ParameterMap |
| typedef std::map< std::string, std::string > | GeometricInfoMap |
| typedef std::map< std::string, std::string > | ExpressionMap |
| typedef std::vector< std::string > | VariableList |
| typedef std::map< std::string, std::string > | TagMap |
| typedef std::map< std::string, std::string > | FilterParams |
| typedef std::vector< std::pair < std::string, FilterParams > > | FilterMap |
| typedef std::map< std::string, CmdLineArg > | CmdLineArgMap |
| typedef std::map< std::string, int > | EnumMap |
| typedef std::map< std::string, EnumMap > | EnumMapList |
| typedef std::map< std::string, std::string > | GloSysInfoMap |
| typedef std::map< std::string, GloSysInfoMap > | GloSysSolnInfoList |
| typedef boost::shared_ptr < Equation > | EquationSharedPtr |
| typedef std::map< std::pair < std::string, int > , FunctionVariableDefinition > | FunctionVariableMap |
| typedef std::map< std::string, FunctionVariableMap > | FunctionMap |
| typedef boost::shared_ptr< Comm > | CommSharedPtr |
| Pointer to a Communicator object. | |
| typedef LibUtilities::NekFactory < std::string, Comm, int, char ** > | CommFactory |
| Datatype of the NekFactory used to instantiate classes derived from the EquationSystem class. | |
| typedef boost::shared_ptr < CommMpi > | CommMpiSharedPtr |
| Pointer to a Communicator object. | |
| typedef boost::shared_ptr < CommSerial > | CommSerialSharedPtr |
| Pointer to a Communicator object. | |
| typedef boost::shared_ptr < Transposition > | TranspositionSharedPtr |
| typedef boost::shared_ptr < NekFFTW > | NekFFTWSharedPtr |
| typedef boost::shared_ptr < NektarFFT > | NektarFFTSharedPtr |
| typedef LibUtilities::NekFactory < std::string, NektarFFT, int > | NektarFFTFactory |
| Datatype of the NekFactory used to instantiate classes derived from the NektarFFT class. | |
| typedef std::vector< BasisKey > | BasisKeyVector |
| Name for a vector of BasisKeys. | |
| typedef std::vector< BasisKey > ::iterator | BasisKeyVectorIter |
| Name for an iterator over a BasisKeyVector. | |
| typedef boost::shared_ptr< Basis > | BasisSharedPtr |
| typedef std::vector < BasisSharedPtr > | BasisVector |
| typedef std::vector < BasisSharedPtr >::iterator | BasisVectorIter |
| typedef Points< NekDouble > | PointsBaseType |
| typedef boost::shared_ptr < Points< NekDouble > > | PointsSharedPtr |
| typedef int | GraphVertexID |
| typedef NekManager< PointsKey, Points< NekDouble > , PointsKey::opLess > | PointsManagerT |
| typedef NekManager< BasisKey, Basis, BasisKey::opLess > | BasisManagerT |
| typedef std::vector< PointsKey > | PointsKeyVector |
| typedef NekDouble(* | PFD )() |
| typedef NekDouble(* | PFD1 )(NekDouble) |
| typedef NekDouble(* | PFD2 )(NekDouble, NekDouble) |
| typedef NekDouble(* | PFD3 )(NekDouble, NekDouble, NekDouble) |
| typedef NekDouble(* | PFD4 )(NekDouble, NekDouble, NekDouble, NekDouble) |
| typedef boost::shared_ptr< Kernel > | KernelSharedPtr |
| typedef boost::shared_ptr < TimeIntegrationScheme > | TimeIntegrationSchemeSharedPtr |
| typedef std::vector < TimeIntegrationSchemeSharedPtr > | TimeIntegrationSchemeVector |
| typedef std::vector < TimeIntegrationSchemeSharedPtr > ::iterator | TimeIntegrationSchemeVectorIter |
| typedef boost::shared_ptr < TimeIntegrationSolution > | TimeIntegrationSolutionSharedPtr |
| typedef std::vector < TimeIntegrationSolutionSharedPtr > | TimeIntegrationSolutionVector |
| typedef std::vector < TimeIntegrationSolutionSharedPtr > ::iterator | TimeIntegrationSolutionVectorIter |
| typedef NekManager < TimeIntegrationSchemeKey, TimeIntegrationScheme, TimeIntegrationSchemeKey::opLess > | TimeIntegrationSchemeManagerT |
| typedef NekFactory < std::string, TimeIntegrationWrapper > | TimeIntegrationWrapperFactory |
| Datatype of the NekFactory used to instantiate classes derived from the EquationSystem class. | |
| typedef boost::shared_ptr < TimeIntegrationWrapper > | TimeIntegrationWrapperSharedPtr |
| typedef boost::shared_ptr < TimeIntegrationIMEXOrder1 > | TimeIntegrationIMEXOrder1SharedPtr |
Functions | |
| void | Write (const std::string &outFile, std::vector< FieldDefinitionsSharedPtr > &fielddefs, std::vector< std::vector< NekDouble > > &fielddata, const FieldMetaDataMap &fieldinfomap=NullFieldMetaDataMap) |
| Write a field file in serial only. | |
| void | Import (const std::string &infilename, std::vector< FieldDefinitionsSharedPtr > &fielddefs, std::vector< std::vector< NekDouble > > &fielddata=NullVectorNekDoubleVector, FieldMetaDataMap &fieldinfomap=NullFieldMetaDataMap, const Array< OneD, int > ElementiDs=NullInt1DArray) |
| Imports an FLD file. | |
| std::string | PortablePath (const boost::filesystem::path &path) |
| create portable path on different platforms for boost::filesystem path | |
| MeshPartitionFactory & | GetMeshPartitionFactory () |
| int | GetNumberOfCoefficients (ShapeType shape, std::vector< unsigned int > &modes, int offset) |
| CommFactory & | GetCommFactory () |
| NektarFFTFactory & | GetNektarFFTFactory () |
| bool | operator< (const BasisKey &lhs, const BasisKey &rhs) |
| bool | operator> (const BasisKey &lhs, const BasisKey &rhs) |
| std::ostream & | operator<< (std::ostream &os, const BasisKey &rhs) |
| bool | operator== (const BasisKey &x, const BasisKey &y) |
| bool | operator== (const BasisKey *x, const BasisKey &y) |
| bool | operator== (const BasisKey &x, const BasisKey *y) |
| bool | operator!= (const BasisKey &x, const BasisKey &y) |
| bool | operator!= (const BasisKey *x, const BasisKey &y) |
| bool | operator!= (const BasisKey &x, const BasisKey *y) |
| static const BasisKey | NullBasisKey (eNoBasisType, 0, NullPointsKey) |
| Defines a null basis with no type or points. | |
| bool | operator== (const GraphVertexObject &x, const GraphVertexObject &y) |
| bool | operator!= (const GraphVertexObject &x, const GraphVertexObject &y) |
| void | Interp1D (const BasisKey &fbasis0, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, Array< OneD, NekDouble > &to) |
this function interpolates a 1D function 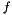 evaluated at the quadrature points of the basis fbasis0 to the function values at the quadrature points of the basis tbasis0 evaluated at the quadrature points of the basis fbasis0 to the function values at the quadrature points of the basis tbasis0 | |
| void | Interp1D (const PointsKey &fpoints0, const Array< OneD, const NekDouble > &from, const PointsKey &tpoints0, Array< OneD, NekDouble > &to) |
| void | Interp1D (const BasisKey &fbasis0, const NekDouble *from, const BasisKey &tbasis0, NekDouble *to) |
| void | Interp1D (const PointsKey &fpoints0, const NekDouble *from, const PointsKey &tpoints0, NekDouble *to) |
| void | Interp2D (const BasisKey &fbasis0, const BasisKey &fbasis1, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, Array< OneD, NekDouble > &to) |
this function interpolates a 2D function 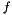 evaluated at the quadrature points of the 2D basis, constructed by fbasis0 and fbasis1, to the function values at the quadrature points of the 2D basis, constructed by tbasis0 and tbasis1 evaluated at the quadrature points of the 2D basis, constructed by fbasis0 and fbasis1, to the function values at the quadrature points of the 2D basis, constructed by tbasis0 and tbasis1 | |
| void | Interp2D (const PointsKey &fpoints0, const PointsKey &fpoints1, const Array< OneD, const NekDouble > &from, const PointsKey &tpoints0, const PointsKey &tpoints1, Array< OneD, NekDouble > &to) |
| void | Interp2D (const PointsKey &fpoints0, const PointsKey &fpoints1, const NekDouble *from, const PointsKey &tpoints0, const PointsKey &tpoints1, NekDouble *to) |
| void | Interp3D (const BasisKey &fbasis0, const BasisKey &fbasis1, const BasisKey &fbasis2, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, const BasisKey &tbasis2, Array< OneD, NekDouble > &to) |
this function interpolates a 3D function 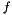 evaluated at the quadrature points of the 3D basis, constructed by fbasis0, fbasis1, and fbasis2 to the function values at the quadrature points of the 3D basis, constructed by tbasis0, tbasis1, and tbasis2. evaluated at the quadrature points of the 3D basis, constructed by fbasis0, fbasis1, and fbasis2 to the function values at the quadrature points of the 3D basis, constructed by tbasis0, tbasis1, and tbasis2. | |
| void | Interp3D (const PointsKey &fpoints0, const PointsKey &fpoints1, const PointsKey &fpoints2, const Array< OneD, const NekDouble > &from, const PointsKey &tpoints0, const PointsKey &tpoints1, const PointsKey &tpoints2, Array< OneD, NekDouble > &to) |
| void | Interp3D (const PointsKey &fpoints0, const PointsKey &fpoints1, const PointsKey &fpoints2, const NekDouble *from, const PointsKey &tpoints0, const PointsKey &tpoints1, const PointsKey &tpoints2, NekDouble *to) |
| void | InterpCoeff1D (const BasisKey &fbasis0, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, Array< OneD, NekDouble > &to) |
| void | InterpCoeff2D (const BasisKey &fbasis0, const BasisKey &fbasis1, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, Array< OneD, NekDouble > &to) |
| void | InterpCoeff2D (const BasisKey &fbasis0, const BasisKey &fbasis1, const NekDouble *from, const BasisKey &tbasis0, const BasisKey &tbasis1, NekDouble *to) |
| void | InterpCoeff3D (const BasisKey &fbasis0, const BasisKey &fbasis1, const BasisKey &fbasis2, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, const BasisKey &tbasis2, Array< OneD, NekDouble > &to) |
| void | InterpCoeff3D (const BasisKey &fbasis0, const BasisKey &fbasis1, const BasisKey &fbasis2, const NekDouble *from, const BasisKey &tbasis0, const BasisKey &tbasis1, const BasisKey &tbasis2, NekDouble *to) |
| PointsManagerT & | PointsManager (void) |
| BasisManagerT & | BasisManager (void) |
| template<typename T > | |
| NekVector< T > | GetColumn (const NekMatrix< T > &matA, int n) |
| NekMatrix< NekDouble > & | SetColumn (NekMatrix< NekDouble > &matA, int n, const NekVector< NekDouble > &x) |
| NekVector< NekDouble > | GetE (int rows, int n) |
| NekMatrix< NekDouble > | Invert (const NekMatrix< NekDouble > &matA) |
| NekMatrix< NekDouble > | GetTranspose (const NekMatrix< NekDouble > &matA) |
| int | GetSize (const Array< OneD, const NekDouble > &x) |
| int | GetSize (const NekVector< NekDouble > &x) |
| NekVector< NekDouble > | ToVector (const Array< OneD, const NekDouble > &x) |
| Array< OneD, NekDouble > | ToArray (const NekVector< NekDouble > &x) |
| NekVector< NekDouble > | Hadamard (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekVector< NekDouble > | VectorPower (const NekVector< NekDouble > &x, NekDouble p) |
| std::string | MatrixToString (const NekMatrix< NekDouble > &A, int precision, NekDouble expSigFigs) |
| std::string | VectorToString (const NekVector< NekDouble > &v, int precision, NekDouble expSigFigs) |
| int | GetTriNumPoints (int degree) |
| int | GetDegree (int nBasisFunctions) |
| int | GetTetNumPoints (int degree) |
| int | GetTetDegree (int nBasisFunc) |
| NekDouble | MakeRound (NekDouble x) |
| NekVector< NekDouble > | MakeDubinerQuadratureSystem (int nBasisFunctions) |
| NekVector< NekDouble > | MakeTetQuadratureSystem (int nBasisFunctions) |
| NekVector< NekDouble > | JacobiPoly (int degree, const NekVector< NekDouble > &x, NekDouble alpha, NekDouble beta) |
| NekDouble | JacobiPoly (int degree, NekDouble x, NekDouble alpha, NekDouble beta) |
| NekVector< NekDouble > | LegendrePoly (int degree, const NekVector< NekDouble > &x) |
| NekVector< NekDouble > | DubinerPoly (int p, int q, const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekVector< NekDouble > | TetrahedralBasis (int p, int q, int r, const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetTetVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetTetVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, int degree) |
| NekMatrix< NekDouble > | GetVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| SharedNekMatrixPtr | MakeVmatrixOfTet (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| SharedNekMatrixPtr | MakeVmatrixOfDubinerPolynomial (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekVector< NekDouble > | MakeTetWeights (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekVector< NekDouble > | MakeQuadratureWeights (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekMatrix< NekDouble > | GetTetInterpolationMatrix (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, const NekVector< NekDouble > &xi, const NekVector< NekDouble > &yi, const NekVector< NekDouble > &zi) |
| NekMatrix< NekDouble > | GetInterpolationMatrix (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &xi, const NekVector< NekDouble > &yi) |
| NekVector< NekDouble > | LegendrePolyDerivative (int degree, const NekVector< NekDouble > &x) |
| NekVector< NekDouble > | DubinerPolyXDerivative (int p, int q, const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekVector< NekDouble > | TetXDerivative (int p, int q, int r, const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetVandermondeForTetXDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetVandermondeForTetXDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| Points< NekDouble > ::MatrixSharedPtrType | GetTetXDerivativeMatrix (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, const NekVector< NekDouble > &xi, const NekVector< NekDouble > &yi, const NekVector< NekDouble > &zi) |
| NekMatrix< NekDouble > | GetVandermondeForXDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, int degree) |
| NekMatrix< NekDouble > | GetVandermondeForXDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| Points< NekDouble > ::MatrixSharedPtrType | GetXDerivativeMatrix (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &xi, const NekVector< NekDouble > &yi) |
| NekVector< NekDouble > | JacobiPolyDerivative (int degree, const NekVector< NekDouble > &x, int alpha, int beta) |
| NekVector< NekDouble > | TetYDerivative (int p, int q, int r, const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetVandermondeForTetYDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetVandermondeForTetYDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| Points< NekDouble > ::MatrixSharedPtrType | GetTetYDerivativeMatrix (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, const NekVector< NekDouble > &xi, const NekVector< NekDouble > &yi, const NekVector< NekDouble > &zi) |
| NekVector< NekDouble > | TetZDerivative (int p, int q, int r, const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetVandermondeForTetZDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetVandermondeForTetZDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| Points< NekDouble > ::MatrixSharedPtrType | GetTetZDerivativeMatrix (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, const NekVector< NekDouble > &xi, const NekVector< NekDouble > &yi, const NekVector< NekDouble > &zi) |
| NekVector< NekDouble > | DubinerPolyYDerivative (int p, int q, const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekMatrix< NekDouble > | GetVandermondeForYDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, int degree) |
| Points< NekDouble > ::MatrixSharedPtrType | GetYDerivativeMatrix (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &xi, const NekVector< NekDouble > &yi) |
| NekMatrix< NekDouble > | GetVandermondeForYDerivative (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekMatrix< NekDouble > | GetMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, int degree) |
| NekMatrix< NekDouble > | GetMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekMatrix< NekDouble > | GetXDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, int degree) |
| NekMatrix< NekDouble > | GetXDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekMatrix< NekDouble > | GetTetXDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetTetXDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetTetYDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetTetYDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetTetZDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z, int degree) |
| NekMatrix< NekDouble > | GetTetZDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, const NekVector< NekDouble > &z) |
| NekMatrix< NekDouble > | GetYDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y, int degree) |
| NekMatrix< NekDouble > | GetYDerivativeOfMonomialVandermonde (const NekVector< NekDouble > &x, const NekVector< NekDouble > &y) |
| NekVector< NekDouble > | GetIntegralOfMonomialVandermonde (int degree) |
| void | PhysGalerkinProject1D (const BasisKey &fbasis0, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, Array< OneD, NekDouble > &to) |
| void | PhysGalerkinProject1D (const PointsKey &fpoints0, const Array< OneD, const NekDouble > &from, const PointsKey &tpoints0, Array< OneD, NekDouble > &to) |
| void | PhysGalerkinProject1D (const BasisKey &fbasis0, const NekDouble *from, const BasisKey &tbasis0, NekDouble *to) |
| void | PhysGalerkinProject1D (const PointsKey &fpoints0, const NekDouble *from, const PointsKey &tpoints0, NekDouble *to) |
| void | PhysGalerkinProject2D (const BasisKey &fbasis0, const BasisKey &fbasis1, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, Array< OneD, NekDouble > &to) |
| void | PhysGalerkinProject2D (const PointsKey &fpoints0, const PointsKey &fpoints1, const Array< OneD, const NekDouble > &from, const PointsKey &tpoints0, const PointsKey &tpoints1, Array< OneD, NekDouble > &to) |
| void | PhysGalerkinProject2D (const PointsKey &fpoints0, const PointsKey &fpoints1, const NekDouble *from, const PointsKey &tpoints0, const PointsKey &tpoints1, NekDouble *to) |
| void | PhysGalerkinProject3D (const BasisKey &fbasis0, const BasisKey &fbasis1, const BasisKey &fbasis2, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, const BasisKey &tbasis2, Array< OneD, NekDouble > &to) |
| void | PhysGalerkinProject3D (const PointsKey &fpoints0, const PointsKey &fpoints1, const PointsKey &fpoints2, const Array< OneD, const NekDouble > &from, const PointsKey &tpoints0, const PointsKey &tpoints1, const PointsKey &tpoints2, Array< OneD, NekDouble > &to) |
| void | PhysGalerkinProject3D (const PointsKey &fpoints0, const PointsKey &fpoints1, const PointsKey &fpoints2, const NekDouble *from, const PointsKey &tpoints0, const PointsKey &tpoints1, const PointsKey &tpoints2, NekDouble *to) |
| bool | operator== (const PointsKey &lhs, const PointsKey &rhs) |
| bool | operator< (const PointsKey &lhs, const PointsKey &rhs) |
| std::ostream & | operator<< (std::ostream &os, const PointsKey &rhs) |
| static const PointsKey | NullPointsKey (0, eNoPointsType) |
| NekDouble | sign (NekDouble arg) |
| NekDouble | awgn (NekDouble sigma) |
| TimeIntegrationSchemeManagerT & | TimeIntegrationSchemeManager (void) |
| bool | operator== (const TimeIntegrationSchemeKey &lhs, const TimeIntegrationSchemeKey &rhs) |
| bool | operator< (const TimeIntegrationSchemeKey &lhs, const TimeIntegrationSchemeKey &rhs) |
| std::ostream & | operator<< (std::ostream &os, const TimeIntegrationSchemeKey &rhs) |
| std::ostream & | operator<< (std::ostream &os, const TimeIntegrationSchemeSharedPtr &rhs) |
| std::ostream & | operator<< (std::ostream &os, const TimeIntegrationScheme &rhs) |
| static const TimeIntegrationSchemeKey | NullTimeIntegrationSchemeKey (eNoTimeIntegrationMethod) |
| TimeIntegrationWrapperFactory & | GetTimeIntegrationWrapperFactory () |
Variables | |
| static std::vector< NekDouble > | NullNekDoubleVector |
| static std::vector < LibUtilities::PointsType > | NullPointsTypeVector |
| static std::vector< unsigned int > | NullUnsignedIntVector |
| static FieldMetaDataMap | NullFieldMetaDataMap |
| static std::vector < std::vector< NekDouble > > | NullVectorNekDoubleVector = boost::assign::list_of(NullNekDoubleVector) |
| const char *const | FunctionTypeMap [] |
| const char *const | ShapeTypeMap [] |
| const unsigned int | ShapeTypeDimMap [SIZE_ShapeType] |
| static BasisSharedPtr | NullBasisSharedPtr |
| static Array< OneD, BasisSharedPtr > | NullBasisSharedPtr1DArray |
| const char *const | BasisTypeMap [] |
| const std::string | kPointsTypeStr [] |
| static const unsigned int | perm4_3d [4][4] = {{0,1,2,3},{3,0,1,2},{2,3,0,1},{1,2,3,0}} |
| static const unsigned int | perm6_3d [6][4] = {{0,1,2,3},{0,2,1,3},{0,2,3,1},{2,0,1,3},{2,0,3,1},{2,3,0,1}} |
| static const unsigned int | perm12A_3d [12][4] |
| static const unsigned int | perm12B_3d [12][4] |
| static const unsigned int | perm12C_3d [12][4] |
| static const unsigned int | perm24_3d [24][4] |
| const unsigned int | NodalTetElecAvailable = 10 |
| static const unsigned int | NodalTetElecNPTS [NodalTetElecAvailable] = {1,2,3,5,6,9,11,15,18,23} |
| static const NekDouble | NodalTetElecData [][9] |
| static const unsigned int | perm3A_2d [3][3] = {{0,1,2},{2,0,1},{0,2,1}} |
| static const unsigned int | perm3B_2d [3][3] = {{0,1,2},{1,0,2},{1,2,0}} |
| static const unsigned int | perm6_2d [6][3] |
| const unsigned int | NodalTriElecAvailable = 16 |
| static const unsigned int | NodalTriElecNPTS [NodalTriElecAvailable] = {1,2,3,4,5,7,8,10,12,14,16,19,21,24,27,30} |
| static const NekDouble | NodalTriElecData [][6] |
| static const unsigned int | perm3A_2d [3][3] = {{0,1,2},{2,0,1},{0,2,1}} |
| static const unsigned int | perm3B_2d [3][3] = {{0,1,2},{1,0,2},{1,2,0}} |
| static const unsigned int | perm3C_2d [3][3] = {{0,1,2},{2,0,1},{1,2,0}} |
| static const unsigned int | perm6_2d [6][3] |
| const unsigned int | NodalTriFeketeAvailable = 16 |
| static const unsigned int | NodalTriFeketeNPTS [NodalTriFeketeAvailable] = {1,2,3,4,5,7,8,10,12,14,16,19,21,24,27,30} |
| static const NekDouble | NodalTriFeketeData [][6] |
| Nektar::LibUtilities::functions | functions_p |
| const char *const | TimeIntegrationMethodMap [] |
| const char *const | TimeIntegrationSchemeTypeMap [] |
| typedef std::vector< BasisKey > Nektar::LibUtilities::BasisKeyVector |
Name for a vector of BasisKeys.
Definition at line 69 of file FoundationsFwd.hpp.
| typedef std::vector< BasisKey >::iterator Nektar::LibUtilities::BasisKeyVectorIter |
Name for an iterator over a BasisKeyVector.
Definition at line 76 of file FoundationsFwd.hpp.
Definition at line 51 of file ManagerAccess.h.
| typedef boost::shared_ptr<Basis> Nektar::LibUtilities::BasisSharedPtr |
Definition at line 79 of file FoundationsFwd.hpp.
| typedef std::vector< BasisSharedPtr > Nektar::LibUtilities::BasisVector |
Definition at line 80 of file FoundationsFwd.hpp.
| typedef std::vector< BasisSharedPtr >::iterator Nektar::LibUtilities::BasisVectorIter |
Definition at line 81 of file FoundationsFwd.hpp.
| typedef std::map< int, std::vector< unsigned int > > Nektar::LibUtilities::BndRegionOrdering |
Definition at line 53 of file MeshPartition.h.
| typedef std::map<std::string, CmdLineArg> Nektar::LibUtilities::CmdLineArgMap |
Definition at line 75 of file SessionReader.h.
| typedef LibUtilities::NekFactory< std::string, Comm, int, char** > Nektar::LibUtilities::CommFactory |
Datatype of the NekFactory used to instantiate classes derived from the EquationSystem class.
| typedef boost::shared_ptr<CommMpi> Nektar::LibUtilities::CommMpiSharedPtr |
| typedef boost::shared_ptr<CommSerial> Nektar::LibUtilities::CommSerialSharedPtr |
Pointer to a Communicator object.
Definition at line 49 of file CommSerial.h.
| typedef boost::shared_ptr<Comm> Nektar::LibUtilities::CommSharedPtr |
| typedef std::map< int, std::vector< unsigned int > > Nektar::LibUtilities::CompositeOrdering |
Definition at line 52 of file MeshPartition.h.
| typedef std::map<std::string, int> Nektar::LibUtilities::EnumMap |
Definition at line 77 of file SessionReader.h.
| typedef std::map<std::string, EnumMap> Nektar::LibUtilities::EnumMapList |
Definition at line 78 of file SessionReader.h.
| typedef boost::shared_ptr<Equation> Nektar::LibUtilities::EquationSharedPtr |
Definition at line 99 of file SessionReader.h.
| typedef std::map<std::string, std::string> Nektar::LibUtilities::ExpressionMap |
Definition at line 61 of file SessionReader.h.
| typedef boost::shared_ptr<FieldDefinitions> Nektar::LibUtilities::FieldDefinitionsSharedPtr |
| typedef boost::shared_ptr<FieldIO> Nektar::LibUtilities::FieldIOSharedPtr |
| typedef std::map<std::string, std::string> Nektar::LibUtilities::FieldMetaDataMap |
| typedef std::vector< std::pair<std::string, FilterParams> > Nektar::LibUtilities::FilterMap |
Definition at line 66 of file SessionReader.h.
| typedef std::map<std::string, std::string> Nektar::LibUtilities::FilterParams |
Definition at line 64 of file SessionReader.h.
| typedef std::map<std::string, FunctionVariableMap > Nektar::LibUtilities::FunctionMap |
Definition at line 115 of file SessionReader.h.
| typedef std::map<std::pair<std::string,int>, FunctionVariableDefinition> Nektar::LibUtilities::FunctionVariableMap |
Definition at line 113 of file SessionReader.h.
| typedef std::map<std::string, std::string> Nektar::LibUtilities::GeometricInfoMap |
Definition at line 60 of file SessionReader.h.
| typedef std::map< std::string, std::string > Nektar::LibUtilities::GloSysInfoMap |
Definition at line 80 of file SessionReader.h.
| typedef std::map< std::string, GloSysInfoMap > Nektar::LibUtilities::GloSysSolnInfoList |
Definition at line 81 of file SessionReader.h.
| typedef int Nektar::LibUtilities::GraphVertexID |
Definition at line 85 of file FoundationsFwd.hpp.
| typedef boost::shared_ptr<Kernel> Nektar::LibUtilities::KernelSharedPtr |
| typedef LibUtilities::NekFactory< std::string, MeshPartition, const SessionReaderSharedPtr& > Nektar::LibUtilities::MeshPartitionFactory |
Datatype of the NekFactory used to instantiate classes derived from the EquationSystem class.
Definition at line 57 of file MeshPartition.h.
| typedef boost::shared_ptr<MeshPartition> Nektar::LibUtilities::MeshPartitionSharedPtr |
Definition at line 243 of file MeshPartition.h.
| typedef boost::shared_ptr<NekFFTW> Nektar::LibUtilities::NekFFTWSharedPtr |
| typedef LibUtilities::NekFactory< std::string, NektarFFT, int> Nektar::LibUtilities::NektarFFTFactory |
Datatype of the NekFactory used to instantiate classes derived from the NektarFFT class.
Definition at line 63 of file NektarFFT.h.
| typedef boost::shared_ptr<NektarFFT> Nektar::LibUtilities::NektarFFTSharedPtr |
Definition at line 56 of file NektarFFT.h.
| typedef std::map<std::string, NekDouble> Nektar::LibUtilities::ParameterMap |
Definition at line 59 of file SessionReader.h.
| typedef NekDouble(* Nektar::LibUtilities::PFD)() |
Definition at line 74 of file AnalyticExpressionEvaluator.cpp.
Definition at line 75 of file AnalyticExpressionEvaluator.cpp.
Definition at line 76 of file AnalyticExpressionEvaluator.cpp.
Definition at line 77 of file AnalyticExpressionEvaluator.cpp.
Definition at line 78 of file AnalyticExpressionEvaluator.cpp.
Definition at line 83 of file FoundationsFwd.hpp.
| typedef std::vector<PointsKey> Nektar::LibUtilities::PointsKeyVector |
| typedef NekManager<PointsKey, Points<NekDouble>, PointsKey::opLess> Nektar::LibUtilities::PointsManagerT |
Definition at line 50 of file ManagerAccess.h.
| typedef boost::shared_ptr<Points<NekDouble> > Nektar::LibUtilities::PointsSharedPtr |
Definition at line 84 of file FoundationsFwd.hpp.
| typedef boost::shared_ptr< SessionReader > Nektar::LibUtilities::SessionReaderSharedPtr |
Definition at line 50 of file MeshPartition.h.
| typedef std::map<std::string, std::string> Nektar::LibUtilities::SolverInfoMap |
Definition at line 58 of file SessionReader.h.
| typedef std::map<std::string, std::string> Nektar::LibUtilities::TagMap |
Definition at line 63 of file SessionReader.h.
| typedef boost::shared_ptr<TimeIntegrationIMEXOrder1> Nektar::LibUtilities::TimeIntegrationIMEXOrder1SharedPtr |
Definition at line 115 of file TimeIntegrationWrapper.h.
| typedef NekManager<TimeIntegrationSchemeKey, TimeIntegrationScheme, TimeIntegrationSchemeKey::opLess> Nektar::LibUtilities::TimeIntegrationSchemeManagerT |
Definition at line 348 of file TimeIntegrationScheme.h.
| typedef boost::shared_ptr<TimeIntegrationScheme> Nektar::LibUtilities::TimeIntegrationSchemeSharedPtr |
Definition at line 51 of file TimeIntegrationScheme.h.
| typedef std::vector<TimeIntegrationSchemeSharedPtr> Nektar::LibUtilities::TimeIntegrationSchemeVector |
Definition at line 55 of file TimeIntegrationScheme.h.
| typedef std::vector<TimeIntegrationSchemeSharedPtr>::iterator Nektar::LibUtilities::TimeIntegrationSchemeVectorIter |
Definition at line 56 of file TimeIntegrationScheme.h.
| typedef boost::shared_ptr<TimeIntegrationSolution> Nektar::LibUtilities::TimeIntegrationSolutionSharedPtr |
Definition at line 57 of file TimeIntegrationScheme.h.
| typedef std::vector<TimeIntegrationSolutionSharedPtr> Nektar::LibUtilities::TimeIntegrationSolutionVector |
Definition at line 58 of file TimeIntegrationScheme.h.
| typedef std::vector<TimeIntegrationSolutionSharedPtr>::iterator Nektar::LibUtilities::TimeIntegrationSolutionVectorIter |
Definition at line 59 of file TimeIntegrationScheme.h.
| typedef NekFactory< std::string, TimeIntegrationWrapper > Nektar::LibUtilities::TimeIntegrationWrapperFactory |
Datatype of the NekFactory used to instantiate classes derived from the EquationSystem class.
Definition at line 46 of file TimeIntegrationWrapper.h.
| typedef boost::shared_ptr<TimeIntegrationWrapper> Nektar::LibUtilities::TimeIntegrationWrapperSharedPtr |
Definition at line 57 of file TimeIntegrationWrapper.h.
| typedef boost::shared_ptr<Transposition> Nektar::LibUtilities::TranspositionSharedPtr |
Definition at line 165 of file Transposition.h.
| typedef std::vector<std::string> Nektar::LibUtilities::VariableList |
Definition at line 62 of file SessionReader.h.
Definition at line 43 of file BasisType.h.
Definition at line 86 of file SessionReader.h.
| eNoPointsType | |
| eGaussGaussLegendre |
1D Gauss-Gauss-Legendre quadrature points |
| eGaussRadauMLegendre |
1D Gauss-Radau-Legendre quadrature points, pinned at x=-1 |
| eGaussRadauPLegendre |
1D Gauss-Radau-Legendre quadrature points, pinned at x=1 |
| eGaussLobattoLegendre |
1D Gauss-Lobatto-Legendre quadrature points |
| eGaussGaussChebyshev |
1D Gauss-Gauss-Chebyshev quadrature points |
| eGaussRadauMChebyshev |
1D Gauss-Radau-Chebyshev quadrature points, pinned at x=-1 |
| eGaussRadauPChebyshev |
1D Gauss-Radau-Chebyshev quadrature points, pinned at x=1 |
| eGaussLobattoChebyshev |
1D Gauss-Lobatto-Legendre quadrature points |
| eGaussRadauMAlpha0Beta1 |
Gauss Radau pinned at x=-1, |
| eGaussRadauMAlpha0Beta2 |
Gauss Radau pinned at x=-1, |
| eGaussRadauMAlpha1Beta0 |
Gauss Radau pinned at x=-1, |
| eGaussRadauMAlpha2Beta0 |
Gauss Radau pinned at x=-1, |
| eGaussKronrodLegendre |
1D Gauss-Kronrod-Legendre quadrature points |
| eGaussRadauKronrodMLegendre |
1D Gauss-Radau-Kronrod-Legendre quadrature points, pinned at x=-1 |
| eGaussRadauKronrodMAlpha1Beta0 |
1D Gauss-Radau-Kronrod-Legendre pinned at x=-1, |
| eGaussLobattoKronrodLegendre |
1D Lobatto Kronrod quadrature points |
| ePolyEvenlySpaced |
1D Evenly-spaced points using Lagrange polynomial |
| eFourierEvenlySpaced |
1D Evenly-spaced points using Fourier Fit |
| eFourierSingleModeSpaced |
1D Non Evenly-spaced points for Single Mode analysis |
| eBoundaryLayerPoints |
1D power law distribution for boundary layer points |
| eBoundaryLayerPointsRev |
1D power law distribution for boundary layer points |
| eNodalTriElec | |
| eNodalTriFekete | |
| eNodalTriEvenlySpaced |
2D Evenly-spaced points on a Triangle |
| eNodalTetEvenlySpaced |
3D Evenly-spaced points on a Tetrahedron |
| eNodalTetElec |
3D Nodal Electrostatic Points on a Tetrahedron |
| eNodalPrismEvenlySpaced |
3D Evenly-spaced points on a Prism |
| SIZE_PointsType |
Length of enum list. |
Definition at line 44 of file PointsType.h.
| eNoShapeType | |
| ePoint | |
| eSegment | |
| eTriangle | |
| eQuadrilateral | |
| eTetrahedron | |
| ePyramid | |
| ePrism | |
| eHexahedron | |
| SIZE_ShapeType |
Definition at line 52 of file ShapeType.hpp.
Definition at line 64 of file TimeIntegrationScheme.h.
Definition at line 133 of file TimeIntegrationScheme.h.
| NekDouble Nektar::LibUtilities::awgn | ( | NekDouble | sigma | ) |
Definition at line 106 of file AnalyticExpressionEvaluator.cpp.
Referenced by Nektar::LibUtilities::functions::functions().
| BasisManagerT & Nektar::LibUtilities::BasisManager | ( | void | ) |
Definition at line 97 of file ManagerAccess.cpp.
Referenced by Nektar::LibUtilities::Basis::CalculateInterpMatrix(), Nektar::MultiRegions::ExpListHomogeneous1D::ExpListHomogeneous1D(), Nektar::MultiRegions::ExpListHomogeneous2D::ExpListHomogeneous2D(), Nektar::LibUtilities::Basis::GenBasis(), InterpCoeff1D(), InterpCoeff2D(), InterpCoeff3D(), Nektar::MultiRegions::ExpListHomogeneous2D::SetPaddingBase(), Nektar::StdRegions::StdExpansion::StdExpansion(), Nektar::MultiRegions::DisContField1D::v_AddTraceIntegral(), and Nektar::StdRegions::StdQuadExp::v_GenMatrix().
| NekVector< NekDouble > Nektar::LibUtilities::DubinerPoly | ( | int | p, |
| int | q, | ||
| const NekVector< NekDouble > & | x, | ||
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 375 of file NodalUtil.cpp.
References GetSize(), JacobiPoly(), and LegendrePoly().
Referenced by GetVandermonde().
| NekVector< NekDouble > Nektar::LibUtilities::DubinerPolyXDerivative | ( | int | p, |
| int | q, | ||
| const NekVector< NekDouble > & | x, | ||
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 664 of file NodalUtil.cpp.
References Nektar::NekVector< DataType >::GetRows(), GetSize(), JacobiPoly(), and LegendrePolyDerivative().
Referenced by GetVandermondeForXDerivative().
| NekVector< NekDouble > Nektar::LibUtilities::DubinerPolyYDerivative | ( | int | p, |
| int | q, | ||
| const NekVector< NekDouble > & | x, | ||
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 1217 of file NodalUtil.cpp.
References GetSize(), JacobiPoly(), JacobiPolyDerivative(), LegendrePoly(), and LegendrePolyDerivative().
Referenced by GetVandermondeForYDerivative().
| NekVector< T > Nektar::LibUtilities::GetColumn | ( | const NekMatrix< T > & | matA, |
| int | n | ||
| ) |
Definition at line 52 of file NodalUtil.cpp.
| CommFactory & Nektar::LibUtilities::GetCommFactory | ( | ) |
Definition at line 64 of file Comm.cpp.
Referenced by Nektar::LibUtilities::SessionReader::CreateComm(), Import(), main(), Nektar::Utilities::InputFld::Process(), and Write().
| int Nektar::LibUtilities::GetDegree | ( | int | nBasisFunctions | ) |
Definition at line 207 of file NodalUtil.cpp.
References ASSERTL1, GetTriNumPoints(), and MakeRound().
Referenced by GetInterpolationMatrix(), GetMonomialVandermonde(), GetVandermonde(), GetVandermondeForXDerivative(), GetVandermondeForYDerivative(), GetXDerivativeMatrix(), GetXDerivativeOfMonomialVandermonde(), GetYDerivativeMatrix(), and GetYDerivativeOfMonomialVandermonde().
Definition at line 72 of file NodalUtil.cpp.
Referenced by Invert().
Definition at line 1588 of file NodalUtil.cpp.
| NekMatrix< NekDouble > Nektar::LibUtilities::GetInterpolationMatrix | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | xi, | ||
| const NekVector< NekDouble > & | yi | ||
| ) |
Definition at line 609 of file NodalUtil.cpp.
References GetDegree(), GetSize(), GetVandermonde(), and Invert().
Referenced by Nektar::LibUtilities::NodalTriElec::CalculateInterpMatrix(), Nektar::LibUtilities::NodalTriEvenlySpaced::CalculateInterpMatrix(), and Nektar::LibUtilities::NodalTriFekete::CalculateInterpMatrix().
| MeshPartitionFactory & Nektar::LibUtilities::GetMeshPartitionFactory | ( | ) |
Definition at line 65 of file MeshPartition.cpp.
Referenced by Nektar::LibUtilities::SessionReader::PartitionMesh(), and Nektar::Utilities::OutputInfo::Process().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| int | degree | ||
| ) |
Definition at line 1327 of file NodalUtil.cpp.
References GetSize().
Referenced by GetMonomialVandermonde().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 1348 of file NodalUtil.cpp.
References GetSize().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 1375 of file NodalUtil.cpp.
References GetMonomialVandermonde(), GetSize(), and GetTetDegree().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 1382 of file NodalUtil.cpp.
References GetDegree(), GetMonomialVandermonde(), and GetSize().
| NektarFFTFactory & Nektar::LibUtilities::GetNektarFFTFactory | ( | ) |
Definition at line 69 of file NektarFFT.cpp.
Referenced by Nektar::AdjointAdvection::DFT(), Nektar::LinearisedAdvection::DFT(), Nektar::MultiRegions::ExpListHomogeneous1D::ExpListHomogeneous1D(), and Nektar::MultiRegions::ExpListHomogeneous2D::ExpListHomogeneous2D().
|
inline |
Definition at line 312 of file ShapeType.hpp.
References ASSERTL0, eHexahedron, ePrism, ePyramid, eQuadrilateral, eSegment, eTetrahedron, eTriangle, Nektar::LibUtilities::StdTriData::getNumberOfCoefficients(), Nektar::LibUtilities::StdTetData::getNumberOfCoefficients(), Nektar::LibUtilities::StdPyrData::getNumberOfCoefficients(), and Nektar::LibUtilities::StdPrismData::getNumberOfCoefficients().
Referenced by Nektar::MultiRegions::ExpListHomogeneous1D::v_ExtractDataToCoeffs(), and Nektar::MultiRegions::ExpList::v_ExtractDataToCoeffs().
| int Nektar::LibUtilities::GetSize | ( | const Array< OneD, const NekDouble > & | x | ) |
Definition at line 111 of file NodalUtil.cpp.
Referenced by Nektar::NekMatrix< DataType, StandardMatrixTag >::CalculateIndex(), DubinerPoly(), DubinerPolyXDerivative(), DubinerPolyYDerivative(), GetInterpolationMatrix(), GetMonomialVandermonde(), GetTetInterpolationMatrix(), GetTetVandermonde(), GetTetXDerivativeMatrix(), GetTetXDerivativeOfMonomialVandermonde(), GetTetYDerivativeOfMonomialVandermonde(), GetTetZDerivativeMatrix(), GetTetZDerivativeOfMonomialVandermonde(), GetVandermonde(), GetVandermondeForTetXDerivative(), GetVandermondeForTetYDerivative(), GetVandermondeForTetZDerivative(), GetVandermondeForXDerivative(), GetVandermondeForYDerivative(), GetXDerivativeMatrix(), GetXDerivativeOfMonomialVandermonde(), GetYDerivativeMatrix(), GetYDerivativeOfMonomialVandermonde(), Hadamard(), JacobiPoly(), JacobiPolyDerivative(), LegendrePoly(), LegendrePolyDerivative(), TetrahedralBasis(), TetXDerivative(), TetYDerivative(), TetZDerivative(), ToArray(), Nektar::StdRegions::ToVector(), and VectorPower().
| int Nektar::LibUtilities::GetSize | ( | const NekVector< NekDouble > & | x | ) |
Definition at line 116 of file NodalUtil.cpp.
References Nektar::NekVector< DataType >::GetRows().
| int Nektar::LibUtilities::GetTetDegree | ( | int | nBasisFunc | ) |
Definition at line 222 of file NodalUtil.cpp.
References ASSERTL1, GetTetNumPoints(), and MakeRound().
Referenced by GetMonomialVandermonde(), GetTetInterpolationMatrix(), GetTetVandermonde(), GetTetXDerivativeMatrix(), GetTetXDerivativeOfMonomialVandermonde(), GetTetYDerivativeOfMonomialVandermonde(), GetTetZDerivativeMatrix(), GetTetZDerivativeOfMonomialVandermonde(), GetVandermondeForTetXDerivative(), GetVandermondeForTetYDerivative(), and GetVandermondeForTetZDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetInterpolationMatrix | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| const NekVector< NekDouble > & | xi, | ||
| const NekVector< NekDouble > & | yi, | ||
| const NekVector< NekDouble > & | zi | ||
| ) |
Definition at line 594 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), GetTetVandermonde(), and Invert().
Referenced by Nektar::LibUtilities::NodalTetElec::CalculateInterpMatrix(), and Nektar::LibUtilities::NodalTetEvenlySpaced::CalculateInterpMatrix().
| int Nektar::LibUtilities::GetTetNumPoints | ( | int | degree | ) |
Definition at line 216 of file NodalUtil.cpp.
Referenced by GetTetDegree().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 477 of file NodalUtil.cpp.
References GetSize(), and TetrahedralBasis().
Referenced by GetTetInterpolationMatrix(), GetTetVandermonde(), GetTetXDerivativeMatrix(), GetTetYDerivativeMatrix(), GetTetZDerivativeMatrix(), and MakeVmatrixOfTet().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 507 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), and GetTetVandermonde().
| Points< NekDouble >::MatrixSharedPtrType Nektar::LibUtilities::GetTetXDerivativeMatrix | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| const NekVector< NekDouble > & | xi, | ||
| const NekVector< NekDouble > & | yi, | ||
| const NekVector< NekDouble > & | zi | ||
| ) |
Definition at line 806 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), GetTetVandermonde(), GetVandermondeForTetXDerivative(), and Invert().
Referenced by Nektar::LibUtilities::NodalTetElec::CalculateDerivMatrix(), and Nektar::LibUtilities::NodalTetEvenlySpaced::CalculateDerivMatrix().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetXDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 1427 of file NodalUtil.cpp.
References GetSize().
Referenced by GetTetXDerivativeOfMonomialVandermonde().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetXDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 1460 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), and GetTetXDerivativeOfMonomialVandermonde().
| Points< NekDouble >::MatrixSharedPtrType Nektar::LibUtilities::GetTetYDerivativeMatrix | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| const NekVector< NekDouble > & | xi, | ||
| const NekVector< NekDouble > & | yi, | ||
| const NekVector< NekDouble > & | zi | ||
| ) |
Definition at line 1047 of file NodalUtil.cpp.
References GetTetVandermonde(), GetVandermondeForTetYDerivative(), and Invert().
Referenced by Nektar::LibUtilities::NodalTetElec::CalculateDerivMatrix(), and Nektar::LibUtilities::NodalTetEvenlySpaced::CalculateDerivMatrix().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetYDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 1468 of file NodalUtil.cpp.
References GetSize().
Referenced by GetTetYDerivativeOfMonomialVandermonde().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetYDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 1502 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), and GetTetYDerivativeOfMonomialVandermonde().
| Points< NekDouble >::MatrixSharedPtrType Nektar::LibUtilities::GetTetZDerivativeMatrix | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| const NekVector< NekDouble > & | xi, | ||
| const NekVector< NekDouble > & | yi, | ||
| const NekVector< NekDouble > & | zi | ||
| ) |
Definition at line 1195 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), GetTetVandermonde(), GetVandermondeForTetZDerivative(), Invert(), and TetZDerivative().
Referenced by Nektar::LibUtilities::NodalTetElec::CalculateDerivMatrix(), and Nektar::LibUtilities::NodalTetEvenlySpaced::CalculateDerivMatrix().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetZDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 1510 of file NodalUtil.cpp.
References GetSize().
Referenced by GetTetZDerivativeOfMonomialVandermonde().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTetZDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 1543 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), and GetTetZDerivativeOfMonomialVandermonde().
| TimeIntegrationWrapperFactory & Nektar::LibUtilities::GetTimeIntegrationWrapperFactory | ( | ) |
Definition at line 42 of file TimeIntegrationWrapper.cpp.
Referenced by Diffusion::TimeIntegrate(), Nektar::SolverUtils::UnsteadySystem::v_InitObject(), and Nektar::SubSteppingExtrapolate::v_SubSteppingTimeIntegration().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetTranspose | ( | const NekMatrix< NekDouble > & | matA | ) |
Definition at line 96 of file NodalUtil.cpp.
| int Nektar::LibUtilities::GetTriNumPoints | ( | int | degree | ) |
Definition at line 202 of file NodalUtil.cpp.
Referenced by GetDegree().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| int | degree | ||
| ) |
Definition at line 515 of file NodalUtil.cpp.
References DubinerPoly(), and GetSize().
Referenced by GetInterpolationMatrix(), GetVandermonde(), GetXDerivativeMatrix(), GetYDerivativeMatrix(), and MakeVmatrixOfDubinerPolynomial().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 540 of file NodalUtil.cpp.
References GetDegree(), GetSize(), and GetVandermonde().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForTetXDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 772 of file NodalUtil.cpp.
References GetSize(), and TetXDerivative().
Referenced by GetTetXDerivativeMatrix(), and GetVandermondeForTetXDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForTetXDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 799 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), and GetVandermondeForTetXDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForTetYDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 1013 of file NodalUtil.cpp.
References GetSize(), and TetYDerivative().
Referenced by GetTetYDerivativeMatrix(), and GetVandermondeForTetYDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForTetYDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 1039 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), and GetVandermondeForTetYDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForTetZDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z, | ||
| int | degree | ||
| ) |
Definition at line 1161 of file NodalUtil.cpp.
References GetSize(), and TetZDerivative().
Referenced by GetTetZDerivativeMatrix(), and GetVandermondeForTetZDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForTetZDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 1187 of file NodalUtil.cpp.
References GetSize(), GetTetDegree(), and GetVandermondeForTetZDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForXDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| int | degree | ||
| ) |
Definition at line 821 of file NodalUtil.cpp.
References DubinerPolyXDerivative(), and GetSize().
Referenced by GetVandermondeForXDerivative(), and GetXDerivativeMatrix().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForXDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 845 of file NodalUtil.cpp.
References GetDegree(), GetSize(), and GetVandermondeForXDerivative().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForYDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| int | degree | ||
| ) |
Definition at line 1280 of file NodalUtil.cpp.
References DubinerPolyYDerivative(), and GetSize().
Referenced by GetVandermondeForYDerivative(), and GetYDerivativeMatrix().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetVandermondeForYDerivative | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 1320 of file NodalUtil.cpp.
References GetDegree(), GetSize(), and GetVandermondeForYDerivative().
| Points< NekDouble >::MatrixSharedPtrType Nektar::LibUtilities::GetXDerivativeMatrix | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | xi, | ||
| const NekVector< NekDouble > & | yi | ||
| ) |
Definition at line 852 of file NodalUtil.cpp.
References GetDegree(), GetSize(), GetVandermonde(), GetVandermondeForXDerivative(), and Invert().
Referenced by Nektar::LibUtilities::NodalTriElec::CalculateDerivMatrix(), Nektar::LibUtilities::NodalTriEvenlySpaced::CalculateDerivMatrix(), and Nektar::LibUtilities::NodalTriFekete::CalculateDerivMatrix().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetXDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| int | degree | ||
| ) |
Definition at line 1389 of file NodalUtil.cpp.
References GetSize().
Referenced by GetXDerivativeOfMonomialVandermonde().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetXDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 1420 of file NodalUtil.cpp.
References GetDegree(), GetSize(), and GetXDerivativeOfMonomialVandermonde().
| Points< NekDouble >::MatrixSharedPtrType Nektar::LibUtilities::GetYDerivativeMatrix | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | xi, | ||
| const NekVector< NekDouble > & | yi | ||
| ) |
Definition at line 1303 of file NodalUtil.cpp.
References GetDegree(), GetSize(), GetVandermonde(), GetVandermondeForYDerivative(), and Invert().
Referenced by Nektar::LibUtilities::NodalTriElec::CalculateDerivMatrix(), Nektar::LibUtilities::NodalTriEvenlySpaced::CalculateDerivMatrix(), and Nektar::LibUtilities::NodalTriFekete::CalculateDerivMatrix().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetYDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| int | degree | ||
| ) |
Definition at line 1551 of file NodalUtil.cpp.
References GetSize().
Referenced by GetYDerivativeOfMonomialVandermonde().
| NekMatrix< NekDouble > Nektar::LibUtilities::GetYDerivativeOfMonomialVandermonde | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 1581 of file NodalUtil.cpp.
References GetDegree(), GetSize(), and GetYDerivativeOfMonomialVandermonde().
| NekVector< NekDouble > Nektar::LibUtilities::Hadamard | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 131 of file NodalUtil.cpp.
References GetSize().
Referenced by LegendrePoly(), LegendrePolyDerivative(), TetYDerivative(), and TetZDerivative().
| void Nektar::LibUtilities::Import | ( | const std::string & | infilename, |
| std::vector< FieldDefinitionsSharedPtr > & | fielddefs, | ||
| std::vector< std::vector< NekDouble > > & | fielddata, | ||
| FieldMetaDataMap & | fieldinfomap, | ||
| const Array< OneD, int > | ElementiDs | ||
| ) |
Imports an FLD file.
This function allows for data to be imported from an FLD file when a session and/or communicator is not instantiated. Typically used in utilities which only operate in serial.
Definition at line 106 of file FieldIO.cpp.
References ASSERTL0, Nektar::LibUtilities::NekFactory< tKey, tBase, >::CreateInstance(), GetCommFactory(), and Nektar::LibUtilities::FieldIO::Import().
Referenced by GetStreakLocation(), Nektar::SolverUtils::EquationSystem::ImportFldToMultiDomains(), and main().
| void Nektar::LibUtilities::Interp1D | ( | const BasisKey & | fbasis0, |
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
this function interpolates a 1D function 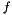 evaluated at the quadrature points of the basis fbasis0 to the function values at the quadrature points of the basis tbasis0
evaluated at the quadrature points of the basis fbasis0 to the function values at the quadrature points of the basis tbasis0
Given a function 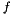 evaluated at the Q quadrature points of the basis fbasis0, this routine calculates, using (Q-1)th order polynomial interpolation, the function values at the Q2 quadrature points of the basis tbasis0.
evaluated at the Q quadrature points of the basis fbasis0, this routine calculates, using (Q-1)th order polynomial interpolation, the function values at the Q2 quadrature points of the basis tbasis0.
| fbasis0 | the basis at which's quadrature points the function is given |
| from | the array containg the function 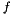 evaluated at the quadrature points of fbasis0 evaluated at the quadrature points of fbasis0 |
| tbasis0 | the basis to which's quadrature points the function should be interpolated |
| to | the array containg the function 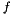 evaluated at the quadrature points of tbasis0 (output of the function) evaluated at the quadrature points of tbasis0 (output of the function) |
Definition at line 54 of file Interp.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey().
Referenced by Nektar::SpatialDomains::GeomFactors::Interp(), Interp1D(), Nektar::LocalRegions::TriExp::v_ComputeEdgeNormal(), Nektar::LocalRegions::QuadExp::v_ComputeEdgeNormal(), Nektar::LocalRegions::NodalTriExp::v_ComputeEdgeNormal(), Nektar::LocalRegions::SegExp::v_ExtractDataToCoeffs(), Nektar::LocalRegions::Expansion::v_GetCoords(), Nektar::LocalRegions::TriExp::v_GetEdgePhysVals(), Nektar::LocalRegions::QuadExp::v_GetEdgePhysVals(), and Nektar::MultiRegions::ExpList1D::v_GetNormals().
| void Nektar::LibUtilities::Interp1D | ( | const PointsKey & | fpoints0, |
| const Array< OneD, const NekDouble > & | from, | ||
| const PointsKey & | tpoints0, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 62 of file Interp.cpp.
References Nektar::eWrapper, Nektar::LibUtilities::PointsKey::GetNumPoints(), PointsManager(), and Vmath::Vcopy().
| void Nektar::LibUtilities::Interp1D | ( | const BasisKey & | fbasis0, |
| const NekDouble * | from, | ||
| const BasisKey & | tbasis0, | ||
| NekDouble * | to | ||
| ) |
Definition at line 84 of file Interp.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey(), and Interp1D().
| void Nektar::LibUtilities::Interp1D | ( | const PointsKey & | fpoints0, |
| const NekDouble * | from, | ||
| const PointsKey & | tpoints0, | ||
| NekDouble * | to | ||
| ) |
Definition at line 92 of file Interp.cpp.
References Nektar::LibUtilities::PointsKey::GetNumPoints(), PointsManager(), and Vmath::Vcopy().
| void Nektar::LibUtilities::Interp2D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
this function interpolates a 2D function 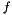 evaluated at the quadrature points of the 2D basis, constructed by fbasis0 and fbasis1, to the function values at the quadrature points of the 2D basis, constructed by tbasis0 and tbasis1
evaluated at the quadrature points of the 2D basis, constructed by fbasis0 and fbasis1, to the function values at the quadrature points of the 2D basis, constructed by tbasis0 and tbasis1
Given a function 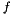 evaluated at the Q quadrature points of the first expansion basis, this routine calculates, using (Q-1)th order polynomial interpolation, the function values at the Q2 quadrature points of the second basis.
evaluated at the Q quadrature points of the first expansion basis, this routine calculates, using (Q-1)th order polynomial interpolation, the function values at the Q2 quadrature points of the second basis.
| fbasis0 | the basis at which's quadrature points the function is given |
| from | the array containg the function 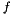 evaluated at the quadrature points of fbasis0 evaluated at the quadrature points of fbasis0 |
| tbasis0 | the basis to which's quadrature points the function should be interpolated |
| to | the array containg the function 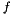 evaluated at the quadrature points of tbasis0 (output of the function) evaluated at the quadrature points of tbasis0 (output of the function) |
Definition at line 116 of file Interp.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey().
Referenced by Nektar::SpatialDomains::GeomFactors::Interp(), Interp2D(), Nektar::SpatialDomains::QuadGeom::QuadGeom(), Nektar::SpatialDomains::TriGeom::TriGeom(), Nektar::LocalRegions::PyrExp::v_ComputeFaceNormal(), Nektar::LocalRegions::TetExp::v_ComputeFaceNormal(), Nektar::LocalRegions::PrismExp::v_ComputeFaceNormal(), Nektar::LocalRegions::QuadExp::v_ExtractDataToCoeffs(), Nektar::LocalRegions::Expansion::v_GetCoords(), Nektar::LocalRegions::PyrExp::v_GetFacePhysVals(), Nektar::LocalRegions::TetExp::v_GetFacePhysVals(), Nektar::LocalRegions::PrismExp::v_GetFacePhysVals(), Nektar::LocalRegions::HexExp::v_GetFacePhysVals(), Nektar::MultiRegions::ExpList2D::v_GetNormals(), and Nektar::MultiRegions::ExpList2D::v_PhysInterp1DScaled().
| void Nektar::LibUtilities::Interp2D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 127 of file Interp.cpp.
References Interp2D().
| void Nektar::LibUtilities::Interp2D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const NekDouble * | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| NekDouble * | to | ||
| ) |
Definition at line 137 of file Interp.cpp.
References Nektar::LibUtilities::PointsKey::GetNumPoints(), PointsManager(), and Vmath::Vcopy().
| void Nektar::LibUtilities::Interp3D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const BasisKey & | fbasis2, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| const BasisKey & | tbasis2, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
this function interpolates a 3D function 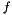 evaluated at the quadrature points of the 3D basis, constructed by fbasis0, fbasis1, and fbasis2 to the function values at the quadrature points of the 3D basis, constructed by tbasis0, tbasis1, and tbasis2.
evaluated at the quadrature points of the 3D basis, constructed by fbasis0, fbasis1, and fbasis2 to the function values at the quadrature points of the 3D basis, constructed by tbasis0, tbasis1, and tbasis2.
Given a function 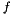 evaluated at the Q quadrature points of the first expansion basis, this routine calculates, using (Q-1)th order polynomial interpolation, the function values at the Q2 quadrature points of the second basis, and the function values at the Q3 quadrature points of the third basis.
evaluated at the Q quadrature points of the first expansion basis, this routine calculates, using (Q-1)th order polynomial interpolation, the function values at the Q2 quadrature points of the second basis, and the function values at the Q3 quadrature points of the third basis.
| fbasis0 | the basis at which's quadrature points the function is given |
| from | the array containg the function 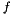 evaluated at the quadrature points of fbasis0 evaluated at the quadrature points of fbasis0 |
| tbasis0 | the basis to which's quadrature points the function should be interpolated |
| to | the array containg the function 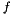 evaluated at the quadrature points of tbasis0 (output of the function) evaluated at the quadrature points of tbasis0 (output of the function) |
Definition at line 178 of file Interp.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey().
Referenced by Nektar::SpatialDomains::GeomFactors::Interp(), Interp3D(), Nektar::LocalRegions::Expansion::v_GetCoords(), and Nektar::MultiRegions::ExpList3D::v_PhysInterp1DScaled().
| void Nektar::LibUtilities::Interp3D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const PointsKey & | fpoints2, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| const PointsKey & | tpoints2, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 194 of file Interp.cpp.
References Interp3D().
| void Nektar::LibUtilities::Interp3D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const PointsKey & | fpoints2, | ||
| const NekDouble * | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| const PointsKey & | tpoints2, | ||
| NekDouble * | to | ||
| ) |
Definition at line 207 of file Interp.cpp.
References Nektar::LibUtilities::PointsKey::GetNumPoints(), and PointsManager().
| void Nektar::LibUtilities::InterpCoeff1D | ( | const BasisKey & | fbasis0, |
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 47 of file InterpCoeff.cpp.
References ASSERTL0, BasisManager(), Nektar::eWrapper, Nektar::LibUtilities::BasisKey::GetBasisType(), Nektar::LibUtilities::BasisKey::GetNumModes(), and Vmath::Vcopy().
Referenced by Nektar::LocalRegions::Expansion2D::v_AddEdgeNormBoundaryInt().
| void Nektar::LibUtilities::InterpCoeff2D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 73 of file InterpCoeff.cpp.
Referenced by Nektar::StdRegions::StdQuadExp::v_ReduceOrderCoeffs(), and Nektar::LocalRegions::QuadExp::v_ReduceOrderCoeffs().
| void Nektar::LibUtilities::InterpCoeff2D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const NekDouble * | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| NekDouble * | to | ||
| ) |
Definition at line 84 of file InterpCoeff.cpp.
References BasisManager(), Nektar::LibUtilities::BasisKey::GetBasisType(), Nektar::LibUtilities::BasisKey::GetNumModes(), and Vmath::Vcopy().
| void Nektar::LibUtilities::InterpCoeff3D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const BasisKey & | fbasis2, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| const BasisKey & | tbasis2, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 125 of file InterpCoeff.cpp.
Referenced by Nektar::LocalRegions::HexExp::v_ReduceOrderCoeffs().
| void Nektar::LibUtilities::InterpCoeff3D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const BasisKey & | fbasis2, | ||
| const NekDouble * | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| const BasisKey & | tbasis2, | ||
| NekDouble * | to | ||
| ) |
Definition at line 138 of file InterpCoeff.cpp.
References BasisManager(), and Nektar::LibUtilities::BasisKey::GetNumModes().
| NekMatrix< NekDouble > Nektar::LibUtilities::Invert | ( | const NekMatrix< NekDouble > & | matA | ) |
Definition at line 79 of file NodalUtil.cpp.
References GetE(), SetColumn(), and Nektar::LinearSystem::Solve().
Referenced by GetInterpolationMatrix(), GetTetInterpolationMatrix(), GetTetXDerivativeMatrix(), GetTetYDerivativeMatrix(), GetTetZDerivativeMatrix(), GetXDerivativeMatrix(), GetYDerivativeMatrix(), and Nektar::NekMatrix< DataType, StandardMatrixTag >::Invert().
| NekVector< NekDouble > Nektar::LibUtilities::JacobiPoly | ( | int | degree, |
| const NekVector< NekDouble > & | x, | ||
| NekDouble | alpha, | ||
| NekDouble | beta | ||
| ) |
Definition at line 253 of file NodalUtil.cpp.
References GetSize().
Referenced by DubinerPoly(), DubinerPolyXDerivative(), DubinerPolyYDerivative(), JacobiPoly(), JacobiPolyDerivative(), TetrahedralBasis(), TetXDerivative(), TetYDerivative(), and TetZDerivative().
| NekDouble Nektar::LibUtilities::JacobiPoly | ( | int | degree, |
| NekDouble | x, | ||
| NekDouble | alpha, | ||
| NekDouble | beta | ||
| ) |
Definition at line 300 of file NodalUtil.cpp.
References JacobiPoly().
| NekVector< NekDouble > Nektar::LibUtilities::JacobiPolyDerivative | ( | int | degree, |
| const NekVector< NekDouble > & | x, | ||
| int | alpha, | ||
| int | beta | ||
| ) |
Definition at line 867 of file NodalUtil.cpp.
References GetSize(), and JacobiPoly().
Referenced by DubinerPolyYDerivative(), TetYDerivative(), and TetZDerivative().
| NekVector< NekDouble > Nektar::LibUtilities::LegendrePoly | ( | int | degree, |
| const NekVector< NekDouble > & | x | ||
| ) |
Definition at line 340 of file NodalUtil.cpp.
References GetSize(), and Hadamard().
Referenced by DubinerPoly(), DubinerPolyYDerivative(), TetrahedralBasis(), TetYDerivative(), and TetZDerivative().
| NekVector< NekDouble > Nektar::LibUtilities::LegendrePolyDerivative | ( | int | degree, |
| const NekVector< NekDouble > & | x | ||
| ) |
Definition at line 624 of file NodalUtil.cpp.
References GetSize(), and Hadamard().
Referenced by DubinerPolyXDerivative(), DubinerPolyYDerivative(), TetXDerivative(), TetYDerivative(), and TetZDerivative().
Definition at line 236 of file NodalUtil.cpp.
Referenced by MakeQuadratureWeights().
| NekVector< NekDouble > Nektar::LibUtilities::MakeQuadratureWeights | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 579 of file NodalUtil.cpp.
References Nektar::NekVector< DataType >::GetRows(), MakeDubinerQuadratureSystem(), MakeVmatrixOfDubinerPolynomial(), and Nektar::LinearSystem::SolveTranspose().
Referenced by Nektar::LibUtilities::NodalTriElec::CalculateWeights(), Nektar::LibUtilities::NodalTriEvenlySpaced::CalculateWeights(), and Nektar::LibUtilities::NodalTriFekete::CalculateWeights().
| NekDouble Nektar::LibUtilities::MakeRound | ( | NekDouble | x | ) |
Definition at line 231 of file NodalUtil.cpp.
Referenced by GetDegree(), GetTetDegree(), MatrixToString(), and VectorToString().
Definition at line 245 of file NodalUtil.cpp.
Referenced by MakeTetWeights().
| NekVector< NekDouble > Nektar::LibUtilities::MakeTetWeights | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 562 of file NodalUtil.cpp.
References Nektar::NekVector< DataType >::GetRows(), MakeTetQuadratureSystem(), MakeVmatrixOfTet(), and Nektar::LinearSystem::SolveTranspose().
Referenced by Nektar::LibUtilities::NodalTetElec::CalculateWeights(), and Nektar::LibUtilities::NodalTetEvenlySpaced::CalculateWeights().
| SharedNekMatrixPtr Nektar::LibUtilities::MakeVmatrixOfDubinerPolynomial | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y | ||
| ) |
Definition at line 554 of file NodalUtil.cpp.
References GetVandermonde().
Referenced by MakeQuadratureWeights().
| SharedNekMatrixPtr Nektar::LibUtilities::MakeVmatrixOfTet | ( | const NekVector< NekDouble > & | x, |
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 547 of file NodalUtil.cpp.
References GetTetVandermonde().
Referenced by MakeTetWeights().
| std::string Nektar::LibUtilities::MatrixToString | ( | const NekMatrix< NekDouble > & | A, |
| int | precision, | ||
| NekDouble | expSigFigs | ||
| ) |
Definition at line 157 of file NodalUtil.cpp.
References MakeRound().
|
static |
Defines a null basis with no type or points.
Referenced by Nektar::MultiRegions::ExpListHomogeneous1D::ExpListHomogeneous1D(), Nektar::MultiRegions::ExpListHomogeneous2D::ExpListHomogeneous2D(), Nektar::SpatialDomains::MeshGraph2D::GetEdgeBasisKey(), Nektar::SpatialDomains::MeshGraph3D::GetFaceBasisKey(), Nektar::StdRegions::StdExpansion::StdExpansion(), Nektar::StdRegions::StdTriExp::v_DetEdgeBasisKey(), Nektar::StdRegions::StdExpansion::v_DetEdgeBasisKey(), Nektar::StdRegions::StdPrismExp::v_DetFaceBasisKey(), Nektar::StdRegions::StdHexExp::v_DetFaceBasisKey(), Nektar::StdRegions::StdTetExp::v_DetFaceBasisKey(), and Nektar::StdRegions::StdExpansion::v_DetFaceBasisKey().
|
static |
Referenced by Nektar::StdRegions::StdExpansion::v_GetFacePointsKey().
|
static |
| bool Nektar::LibUtilities::operator!= | ( | const GraphVertexObject & | x, |
| const GraphVertexObject & | y | ||
| ) |
Definition at line 76 of file Graph.cpp.
References Nektar::LibUtilities::GraphVertexObject::m_id.
| bool Nektar::LibUtilities::operator!= | ( | const BasisKey & | x, |
| const BasisKey & | y | ||
| ) |
| bool Nektar::LibUtilities::operator!= | ( | const BasisKey * | x, |
| const BasisKey & | y | ||
| ) |
| bool Nektar::LibUtilities::operator!= | ( | const BasisKey & | x, |
| const BasisKey * | y | ||
| ) |
| bool Nektar::LibUtilities::operator< | ( | const BasisKey & | lhs, |
| const BasisKey & | rhs | ||
| ) |
Definition at line 49 of file Basis.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey(), Nektar::LibUtilities::BasisKey::m_basistype, and Nektar::LibUtilities::BasisKey::m_nummodes.
| bool Nektar::LibUtilities::operator< | ( | const PointsKey & | lhs, |
| const PointsKey & | rhs | ||
| ) |
Definition at line 55 of file Points.cpp.
References Nektar::LibUtilities::PointsKey::m_factor, Nektar::LibUtilities::PointsKey::m_numpoints, and Nektar::LibUtilities::PointsKey::m_pointstype.
| bool Nektar::LibUtilities::operator< | ( | const TimeIntegrationSchemeKey & | lhs, |
| const TimeIntegrationSchemeKey & | rhs | ||
| ) |
Definition at line 58 of file TimeIntegrationScheme.cpp.
References Nektar::LibUtilities::TimeIntegrationSchemeKey::m_method.
| std::ostream & Nektar::LibUtilities::operator<< | ( | std::ostream & | os, |
| const TimeIntegrationSchemeKey & | rhs | ||
| ) |
Definition at line 68 of file TimeIntegrationScheme.cpp.
References Nektar::LibUtilities::TimeIntegrationSchemeKey::GetIntegrationMethod(), and TimeIntegrationMethodMap.
| std::ostream & Nektar::LibUtilities::operator<< | ( | std::ostream & | os, |
| const BasisKey & | rhs | ||
| ) |
Definition at line 85 of file Basis.cpp.
References BasisTypeMap, Nektar::LibUtilities::BasisKey::GetBasisType(), Nektar::LibUtilities::BasisKey::GetNumModes(), and Nektar::LibUtilities::BasisKey::GetPointsKey().
Referenced by operator<<().
| std::ostream & Nektar::LibUtilities::operator<< | ( | std::ostream & | os, |
| const PointsKey & | rhs | ||
| ) |
Definition at line 95 of file Points.cpp.
References Nektar::LibUtilities::PointsKey::GetNumPoints(), Nektar::LibUtilities::PointsKey::GetPointsType(), and kPointsTypeStr.
| std::ostream & Nektar::LibUtilities::operator<< | ( | std::ostream & | os, |
| const TimeIntegrationSchemeSharedPtr & | rhs | ||
| ) |
Definition at line 1771 of file TimeIntegrationScheme.cpp.
References operator<<().
| std::ostream & Nektar::LibUtilities::operator<< | ( | std::ostream & | os, |
| const TimeIntegrationScheme & | rhs | ||
| ) |
Definition at line 1776 of file TimeIntegrationScheme.cpp.
References Nektar::LibUtilities::TimeIntegrationScheme::A(), Nektar::LibUtilities::TimeIntegrationScheme::A_IMEX(), Nektar::LibUtilities::TimeIntegrationScheme::B(), Nektar::LibUtilities::TimeIntegrationScheme::B_IMEX(), eIMEX, Nektar::LibUtilities::TimeIntegrationScheme::GetIntegrationMethod(), Nektar::LibUtilities::TimeIntegrationScheme::GetIntegrationSchemeType(), Nektar::LibUtilities::TimeIntegrationScheme::GetNstages(), Nektar::LibUtilities::TimeIntegrationScheme::GetNsteps(), TimeIntegrationMethodMap, TimeIntegrationSchemeTypeMap, Nektar::LibUtilities::TimeIntegrationScheme::U(), and Nektar::LibUtilities::TimeIntegrationScheme::V().
| bool Nektar::LibUtilities::operator== | ( | const PointsKey & | lhs, |
| const PointsKey & | rhs | ||
| ) |
Definition at line 49 of file Points.cpp.
References Nektar::LibUtilities::PointsKey::m_numpoints, and Nektar::LibUtilities::PointsKey::m_pointstype.
| bool Nektar::LibUtilities::operator== | ( | const TimeIntegrationSchemeKey & | lhs, |
| const TimeIntegrationSchemeKey & | rhs | ||
| ) |
Definition at line 53 of file TimeIntegrationScheme.cpp.
References Nektar::LibUtilities::TimeIntegrationSchemeKey::m_method.
| bool Nektar::LibUtilities::operator== | ( | const GraphVertexObject & | x, |
| const GraphVertexObject & | y | ||
| ) |
Definition at line 71 of file Graph.cpp.
References Nektar::LibUtilities::GraphVertexObject::m_id.
| bool Nektar::LibUtilities::operator== | ( | const BasisKey & | x, |
| const BasisKey & | y | ||
| ) |
Definition at line 703 of file Basis.cpp.
References Nektar::LibUtilities::BasisKey::GetNumModes(), Nektar::LibUtilities::BasisKey::GetPointsKey(), and Nektar::LibUtilities::BasisKey::m_basistype.
| bool Nektar::LibUtilities::operator== | ( | const BasisKey * | x, |
| const BasisKey & | y | ||
| ) |
| bool Nektar::LibUtilities::operator== | ( | const BasisKey & | x, |
| const BasisKey * | y | ||
| ) |
| bool Nektar::LibUtilities::operator> | ( | const BasisKey & | lhs, |
| const BasisKey & | rhs | ||
| ) |
| void Nektar::LibUtilities::PhysGalerkinProject1D | ( | const BasisKey & | fbasis0, |
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 53 of file PhysGalerkinProject.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey().
Referenced by PhysGalerkinProject1D().
| void Nektar::LibUtilities::PhysGalerkinProject1D | ( | const PointsKey & | fpoints0, |
| const Array< OneD, const NekDouble > & | from, | ||
| const PointsKey & | tpoints0, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 61 of file PhysGalerkinProject.cpp.
References Nektar::eWrapper, Nektar::LibUtilities::PointsKey::GetNumPoints(), PointsManager(), and Vmath::Vcopy().
| void Nektar::LibUtilities::PhysGalerkinProject1D | ( | const BasisKey & | fbasis0, |
| const NekDouble * | from, | ||
| const BasisKey & | tbasis0, | ||
| NekDouble * | to | ||
| ) |
Definition at line 84 of file PhysGalerkinProject.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey(), and PhysGalerkinProject1D().
| void Nektar::LibUtilities::PhysGalerkinProject1D | ( | const PointsKey & | fpoints0, |
| const NekDouble * | from, | ||
| const PointsKey & | tpoints0, | ||
| NekDouble * | to | ||
| ) |
Definition at line 92 of file PhysGalerkinProject.cpp.
References Nektar::LibUtilities::PointsKey::GetNumPoints(), PointsManager(), and Vmath::Vcopy().
| void Nektar::LibUtilities::PhysGalerkinProject2D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 116 of file PhysGalerkinProject.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey().
Referenced by PhysGalerkinProject2D(), and Nektar::MultiRegions::ExpList2D::v_PhysGalerkinProjection1DScaled().
| void Nektar::LibUtilities::PhysGalerkinProject2D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 127 of file PhysGalerkinProject.cpp.
References PhysGalerkinProject2D().
| void Nektar::LibUtilities::PhysGalerkinProject2D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const NekDouble * | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| NekDouble * | to | ||
| ) |
Definition at line 137 of file PhysGalerkinProject.cpp.
References Nektar::LibUtilities::PointsKey::GetNumPoints(), PointsManager(), and Vmath::Vcopy().
| void Nektar::LibUtilities::PhysGalerkinProject3D | ( | const BasisKey & | fbasis0, |
| const BasisKey & | fbasis1, | ||
| const BasisKey & | fbasis2, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const BasisKey & | tbasis0, | ||
| const BasisKey & | tbasis1, | ||
| const BasisKey & | tbasis2, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 178 of file PhysGalerkinProject.cpp.
References Nektar::LibUtilities::BasisKey::GetPointsKey().
Referenced by PhysGalerkinProject3D(), and Nektar::MultiRegions::ExpList3D::v_PhysGalerkinProjection1DScaled().
| void Nektar::LibUtilities::PhysGalerkinProject3D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const PointsKey & | fpoints2, | ||
| const Array< OneD, const NekDouble > & | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| const PointsKey & | tpoints2, | ||
| Array< OneD, NekDouble > & | to | ||
| ) |
Definition at line 197 of file PhysGalerkinProject.cpp.
References PhysGalerkinProject3D().
| void Nektar::LibUtilities::PhysGalerkinProject3D | ( | const PointsKey & | fpoints0, |
| const PointsKey & | fpoints1, | ||
| const PointsKey & | fpoints2, | ||
| const NekDouble * | from, | ||
| const PointsKey & | tpoints0, | ||
| const PointsKey & | tpoints1, | ||
| const PointsKey & | tpoints2, | ||
| NekDouble * | to | ||
| ) |
Definition at line 210 of file PhysGalerkinProject.cpp.
References Nektar::LibUtilities::PointsKey::GetNumPoints(), and PointsManager().
| PointsManagerT & Nektar::LibUtilities::PointsManager | ( | void | ) |
Definition at line 92 of file ManagerAccess.cpp.
Referenced by Nektar::LibUtilities::GaussPoints::CalculateGalerkinProjectionMatrix(), Nektar::LibUtilities::PolyEPoints::CalculateWeights(), Nektar::LibUtilities::BLPoints::CreateMatrix(), Nektar::LibUtilities::FourierPoints::CreateMatrix(), Nektar::LibUtilities::FourierSingleModePoints::CreateMatrix(), Nektar::LibUtilities::GaussPoints::CreateMatrix(), Nektar::LibUtilities::Basis::GenBasis(), Nektar::LibUtilities::NodalTetElec::GetI(), Nektar::LibUtilities::NodalTriElec::GetI(), Nektar::LibUtilities::PolyEPoints::GetI(), Nektar::LibUtilities::NodalTriEvenlySpaced::GetI(), Nektar::LibUtilities::NodalPrismEvenlySpaced::GetI(), Nektar::LibUtilities::NodalTetEvenlySpaced::GetI(), Nektar::LibUtilities::NodalTriFekete::GetI(), Nektar::StdRegions::StdNodalPrismExp::GetNodalPoints(), Nektar::StdRegions::StdNodalTetExp::GetNodalPoints(), Nektar::StdRegions::StdNodalTriExp::GetNodalPoints(), Interp1D(), Interp2D(), Interp3D(), Nektar::Utilities::InputNek::LoadHOSurfaces(), PhysGalerkinProject1D(), PhysGalerkinProject2D(), PhysGalerkinProject3D(), Nektar::MultiRegions::ExpList1D::PostProcess(), Nektar::Utilities::ProcessBL::Process(), Nektar::Utilities::ProcessTetSplit::Process(), Nektar::SpatialDomains::SegGeom::SegGeom(), and Nektar::SpatialDomains::TriGeom::TriGeom().
| std::string Nektar::LibUtilities::PortablePath | ( | const boost::filesystem::path & | path | ) |
create portable path on different platforms for boost::filesystem path
Definition at line 41 of file FileSystem.cpp.
Referenced by Nektar::SolverUtils::UnsteadySystem::CheckForRestartTime(), Nektar::LibUtilities::SessionReader::GetSessionNameRank(), Nektar::LibUtilities::FieldIO::Import(), Nektar::LibUtilities::SessionReader::PartitionMesh(), Nektar::LibUtilities::FieldIO::SetUpOutput(), Nektar::LibUtilities::MeshPartition::WriteAllPartitions(), and Nektar::LibUtilities::MeshPartition::WriteLocalPartition().
| NekMatrix< NekDouble > & Nektar::LibUtilities::SetColumn | ( | NekMatrix< NekDouble > & | matA, |
| int | n, | ||
| const NekVector< NekDouble > & | x | ||
| ) |
Definition at line 62 of file NodalUtil.cpp.
Referenced by Invert().
| NekDouble Nektar::LibUtilities::sign | ( | NekDouble | arg | ) |
Definition at line 97 of file AnalyticExpressionEvaluator.cpp.
Referenced by Nektar::LibUtilities::AnalyticExpressionEvaluator::AnalyticExpressionEvaluator().
| NekVector< NekDouble > Nektar::LibUtilities::TetrahedralBasis | ( | int | p, |
| int | q, | ||
| int | r, | ||
| const NekVector< NekDouble > & | x, | ||
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 415 of file NodalUtil.cpp.
References GetSize(), JacobiPoly(), and LegendrePoly().
Referenced by GetTetVandermonde().
| NekVector< NekDouble > Nektar::LibUtilities::TetXDerivative | ( | int | p, |
| int | q, | ||
| int | r, | ||
| const NekVector< NekDouble > & | x, | ||
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 711 of file NodalUtil.cpp.
References Nektar::NekVector< DataType >::GetRows(), GetSize(), JacobiPoly(), and LegendrePolyDerivative().
Referenced by GetVandermondeForTetXDerivative().
| NekVector< NekDouble > Nektar::LibUtilities::TetYDerivative | ( | int | p, |
| int | q, | ||
| int | r, | ||
| const NekVector< NekDouble > & | x, | ||
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 886 of file NodalUtil.cpp.
References GetSize(), Hadamard(), JacobiPoly(), JacobiPolyDerivative(), LegendrePoly(), LegendrePolyDerivative(), and VectorPower().
Referenced by GetVandermondeForTetYDerivative().
| NekVector< NekDouble > Nektar::LibUtilities::TetZDerivative | ( | int | p, |
| int | q, | ||
| int | r, | ||
| const NekVector< NekDouble > & | x, | ||
| const NekVector< NekDouble > & | y, | ||
| const NekVector< NekDouble > & | z | ||
| ) |
Definition at line 1064 of file NodalUtil.cpp.
References GetSize(), Hadamard(), JacobiPoly(), JacobiPolyDerivative(), LegendrePoly(), LegendrePolyDerivative(), and VectorPower().
Referenced by GetTetZDerivativeMatrix(), and GetVandermondeForTetZDerivative().
| TimeIntegrationSchemeManagerT & Nektar::LibUtilities::TimeIntegrationSchemeManager | ( | void | ) |
Definition at line 45 of file TimeIntegrationScheme.cpp.
References Nektar::LibUtilities::TimeIntegrationScheme::Create(), and Nektar::LibUtilities::NekManager< KeyType, ValueT, opLessCreator >::RegisterGlobalCreator().
Referenced by Nektar::LibUtilities::TimeIntegrationIMEXOrder1::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXOrder2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXOrder3::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_1_1_1::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_1_2_1::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_1_2_2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_4_4_3::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_2_2_2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_2_3_3::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_2_3_2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXdirk_3_4_3::v_InitObject(), Nektar::LibUtilities::TimeIntegrationForwardEuler::v_InitObject(), Nektar::LibUtilities::TimeIntegrationBackwardEuler::v_InitObject(), Nektar::LibUtilities::TimeIntegrationBDFImplicitOrder1::v_InitObject(), Nektar::LibUtilities::TimeIntegrationBDFImplicitOrder2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationRungeKutta2_ImprovedEuler::v_InitObject(), Nektar::LibUtilities::TimeIntegrationRungeKutta2_ModifiedEuler::v_InitObject(), Nektar::LibUtilities::TimeIntegrationClassicalRungeKutta4::v_InitObject(), Nektar::LibUtilities::TimeIntegrationDIRKOrder2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationDIRKOrder3::v_InitObject(), Nektar::LibUtilities::TimeIntegrationMidpoint::v_InitObject(), Nektar::LibUtilities::TimeIntegrationAdamsBashforthOrder2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationAdamsBashforthOrder3::v_InitObject(), Nektar::LibUtilities::TimeIntegrationAdamsMoultonOrder2::v_InitObject(), Nektar::LibUtilities::TimeIntegrationIMEXGear::v_InitObject(), Nektar::LibUtilities::TimeIntegrationCNAB::v_InitObject(), and Nektar::LibUtilities::TimeIntegrationMCNAB::v_InitObject().
Definition at line 126 of file NodalUtil.cpp.
References Nektar::NekVector< DataType >::GetPtr(), and GetSize().
Definition at line 121 of file NodalUtil.cpp.
References GetSize().
| NekVector< NekDouble > Nektar::LibUtilities::VectorPower | ( | const NekVector< NekDouble > & | x, |
| NekDouble | p | ||
| ) |
Definition at line 143 of file NodalUtil.cpp.
References GetSize().
Referenced by TetYDerivative(), and TetZDerivative().
| std::string Nektar::LibUtilities::VectorToString | ( | const NekVector< NekDouble > & | v, |
| int | precision, | ||
| NekDouble | expSigFigs | ||
| ) |
Definition at line 183 of file NodalUtil.cpp.
References Nektar::NekVector< DataType >::GetRows(), and MakeRound().
| void Nektar::LibUtilities::Write | ( | const std::string & | outFile, |
| std::vector< FieldDefinitionsSharedPtr > & | fielddefs, | ||
| std::vector< std::vector< NekDouble > > & | fielddata, | ||
| const FieldMetaDataMap & | fieldinfomap | ||
| ) |
Write a field file in serial only.
This function allows for data to be written to an FLD file when a session and/or communicator is not instantiated. Typically used in utilities which do not take XML input and operate in serial only.
Definition at line 72 of file FieldIO.cpp.
References ASSERTL0, Nektar::LibUtilities::NekFactory< tKey, tBase, >::CreateInstance(), GetCommFactory(), and Nektar::LibUtilities::FieldIO::Write().
Referenced by CalcNonLinearForcing(), main(), WriteBcs(), Writefield(), WriteFld(), Nektar::LinearisedAdvection::WriteFldBase(), and Nektar::PulseWaveSystem::WriteVessels().
| const char* const Nektar::LibUtilities::BasisTypeMap[] |
Definition at line 47 of file Foundations.hpp.
Referenced by Nektar::LibUtilities::FieldIO::ImportFieldDefs(), operator<<(), Nektar::SpatialDomains::MeshGraph::ReadExpansions(), Nektar::SpatialDomains::MeshGraph::SetExpansions(), and Nektar::LibUtilities::FieldIO::Write().
|
static |
| const char* const Nektar::LibUtilities::FunctionTypeMap[] |
Definition at line 92 of file SessionReader.h.
| const std::string Nektar::LibUtilities::kPointsTypeStr[] |
Definition at line 69 of file Foundations.hpp.
Referenced by Nektar::LibUtilities::FieldIO::ImportFieldDefs(), operator<<(), Nektar::SpatialDomains::MeshGraph::ReadCurves(), Nektar::SpatialDomains::MeshGraph::ReadExpansions(), and Nektar::Utilities::OutputNekpp::WriteXmlCurves().
| const unsigned int Nektar::LibUtilities::NodalTetElecAvailable = 10 |
Definition at line 23 of file NodalTetElecData.h.
|
static |
Definition at line 25 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
|
static |
Definition at line 24 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
| const unsigned int Nektar::LibUtilities::NodalTriElecAvailable = 16 |
Definition at line 10 of file NodalTriElecData.h.
|
static |
Definition at line 12 of file NodalTriElecData.h.
Referenced by Nektar::LibUtilities::NodalTriElec::CalculatePoints().
|
static |
Definition at line 11 of file NodalTriElecData.h.
Referenced by Nektar::LibUtilities::NodalTriElec::CalculatePoints().
| const unsigned int Nektar::LibUtilities::NodalTriFeketeAvailable = 16 |
Definition at line 10 of file NodalTriFeketeData.h.
|
static |
Definition at line 12 of file NodalTriFeketeData.h.
Referenced by Nektar::LibUtilities::NodalTriFekete::CalculatePoints().
|
static |
Definition at line 11 of file NodalTriFeketeData.h.
Referenced by Nektar::LibUtilities::NodalTriFekete::CalculatePoints().
|
static |
Definition at line 358 of file Basis.h.
Referenced by Nektar::MultiRegions::ExpList::v_GetHomogeneousBasis().
|
static |
|
static |
Definition at line 66 of file FieldIO.h.
Referenced by Nektar::LibUtilities::FieldIO::AddInfoTag(), Nektar::SolverUtils::UnsteadySystem::CheckForRestartTime(), Nektar::SolverUtils::EquationSystem::EvaluateFunction(), Nektar::Utilities::InputFld::Process(), Nektar::Utilities::ProcessInterpPoints::Process(), Nektar::Utilities::ProcessInterpField::Process(), and Nektar::Utilities::ProcessAddFld::Process().
|
static |
|
static |
|
static |
|
static |
Definition at line 67 of file FieldIO.h.
Referenced by Nektar::LibUtilities::FieldIO::Import().
|
static |
Definition at line 9 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
|
static |
Definition at line 11 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
|
static |
Definition at line 13 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
|
static |
Definition at line 16 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
|
static |
Definition at line 5 of file NodalTriFeketeData.h.
|
static |
Definition at line 6 of file NodalTriElecData.h.
Referenced by Nektar::LibUtilities::NodalTriElec::CalculatePoints(), and Nektar::LibUtilities::NodalTriFekete::CalculatePoints().
|
static |
Definition at line 6 of file NodalTriFeketeData.h.
|
static |
Definition at line 7 of file NodalTriElecData.h.
Referenced by Nektar::LibUtilities::NodalTriElec::CalculatePoints(), and Nektar::LibUtilities::NodalTriFekete::CalculatePoints().
|
static |
Definition at line 7 of file NodalTriFeketeData.h.
|
static |
Definition at line 6 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
|
static |
Definition at line 8 of file NodalTriFeketeData.h.
|
static |
Definition at line 8 of file NodalTriElecData.h.
Referenced by Nektar::LibUtilities::NodalTriElec::CalculatePoints(), and Nektar::LibUtilities::NodalTriFekete::CalculatePoints().
|
static |
Definition at line 7 of file NodalTetElecData.h.
Referenced by Nektar::LibUtilities::NodalTetElec::CalculatePoints().
| const unsigned int Nektar::LibUtilities::ShapeTypeDimMap[SIZE_ShapeType] |
Definition at line 81 of file ShapeType.hpp.
Referenced by Nektar::StdRegions::operator<(), Nektar::StdRegions::operator<<(), and Nektar::StdRegions::operator==().
| const char* const Nektar::LibUtilities::ShapeTypeMap[] |
Definition at line 66 of file ShapeType.hpp.
Referenced by Nektar::LibUtilities::FieldIO::ImportFieldDefs(), Nektar::MultiRegions::operator<<(), Nektar::StdRegions::operator<<(), and Nektar::LibUtilities::FieldIO::Write().
| const char* const Nektar::LibUtilities::TimeIntegrationMethodMap[] |
Definition at line 99 of file TimeIntegrationScheme.h.
Referenced by operator<<(), Nektar::VelocityCorrectionScheme::v_GenerateSummary(), and Nektar::SolverUtils::UnsteadySystem::v_GenerateSummary().
| const char* const Nektar::LibUtilities::TimeIntegrationSchemeTypeMap[] |
Definition at line 142 of file TimeIntegrationScheme.h.
Referenced by operator<<().
 1.8.1.2
1.8.1.2