Nektar++
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
Public Member Functions | Static Public Member Functions | Public Attributes | Static Public Attributes | Protected Member Functions | Private Member Functions | Private Attributes | Friends | List of all members
Nektar::CoupledLinearNS Class Reference

#include <CoupledLinearNS.h>

Inheritance diagram for Nektar::CoupledLinearNS:
Inheritance graph
[legend]
Collaboration diagram for Nektar::CoupledLinearNS:
Collaboration graph
[legend]

Public Member Functions

void SetUpCoupledMatrix (const NekDouble lambda=0.0, const Array< OneD, Array< OneD, NekDouble > > &Advfield=NullNekDoubleArrayofArray, bool IsLinearNSEquation=true)
const
SpatialDomains::ExpansionMap & 		GenPressureExp (const SpatialDomains::ExpansionMap &VelExp)
void Solve (void)
void SolveLinearNS (const Array< OneD, Array< OneD, NekDouble > > &forcing)
void SolveLinearNS (const Array< OneD, Array< OneD, NekDouble > > &forcing, Array< OneD, MultiRegions::ExpListSharedPtr > &fields, MultiRegions::ExpListSharedPtr &pressure, const int HomogeneousMode=0)
void SolveUnsteadyStokesSystem (const Array< OneD, const Array< OneD, NekDouble > > &inarray, Array< OneD, Array< OneD, NekDouble > > &outarray, const NekDouble time, const NekDouble a_iixDt)
void EvaluateAdvection (const Array< OneD, const Array< OneD, NekDouble > > &inarray, Array< OneD, Array< OneD, NekDouble > > &outarray, const NekDouble time)
void SolveSteadyNavierStokes (void)
void Continuation (void)
void EvaluateNewtonRHS (Array< OneD, Array< OneD, NekDouble > > &Velocity, Array< OneD, Array< OneD, NekDouble > > &outarray)
void InfNorm (Array< OneD, Array< OneD, NekDouble > > &inarray, Array< OneD, NekDouble > &outarray)
void L2Norm (Array< OneD, Array< OneD, NekDouble > > &inarray, Array< OneD, NekDouble > &outarray)
void DefineForcingTerm (void)
- Public Member Functions inherited from Nektar::IncNavierStokes
virtual ~IncNavierStokes ()
virtual void v_GetFluxVector (const int i, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &flux)
virtual void v_NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numflux)
int GetNConvectiveFields (void)
Array< OneD, int > & GetVelocity (void)
Array< OneD, NekDouble > GetElmtCFLVals (void)
NekDouble GetCFLEstimate (int &elmtid)
void AddForcing (const SolverUtils::ForcingSharedPtr &pForce)
- Public Member Functions inherited from Nektar::SolverUtils::AdvectionSystem
SOLVER_UTILS_EXPORT AdvectionSystem (const LibUtilities::SessionReaderSharedPtr &pSession)
virtual SOLVER_UTILS_EXPORT ~AdvectionSystem ()
AdvectionSharedPtr GetAdvObject ()
 Returns the advection object held by this instance.
- Public Member Functions inherited from Nektar::SolverUtils::UnsteadySystem
virtual SOLVER_UTILS_EXPORT ~UnsteadySystem ()
 Destructor.
SOLVER_UTILS_EXPORT NekDouble GetTimeStep (const Array< OneD, const Array< OneD, NekDouble > > &inarray)
 Calculate the larger time-step mantaining the problem stable.
- Public Member Functions inherited from Nektar::SolverUtils::EquationSystem
virtual SOLVER_UTILS_EXPORT ~EquationSystem ()
 Destructor.
SOLVER_UTILS_EXPORT void SetUpTraceNormals (void)
SOLVER_UTILS_EXPORT void InitObject ()
 Initialises the members of this object.
SOLVER_UTILS_EXPORT void DoInitialise ()
 Perform any initialisation necessary before solving the problem.
SOLVER_UTILS_EXPORT void DoSolve ()
 Solve the problem.
SOLVER_UTILS_EXPORT void TransCoeffToPhys ()
 Transform from coefficient to physical space.
SOLVER_UTILS_EXPORT void TransPhysToCoeff ()
 Transform from physical to coefficient space.
SOLVER_UTILS_EXPORT void Output ()
 Perform output operations after solve.
SOLVER_UTILS_EXPORT NekDouble LinfError (unsigned int field, const Array< OneD, NekDouble > &exactsoln=NullNekDouble1DArray)
 Linf error computation.
SOLVER_UTILS_EXPORT std::string GetSessionName ()
 Get Session name.
template<class T >
boost::shared_ptr< T > as ()
SOLVER_UTILS_EXPORT void ResetSessionName (std::string newname)
 Reset Session name.
SOLVER_UTILS_EXPORT
LibUtilities::SessionReaderSharedPtr 		GetSession ()
 Get Session name.
SOLVER_UTILS_EXPORT
MultiRegions::ExpListSharedPtr 		GetPressure ()
 Get pressure field if available.
SOLVER_UTILS_EXPORT void PrintSummary (std::ostream &out)
 Print a summary of parameters and solver characteristics.
SOLVER_UTILS_EXPORT void SetLambda (NekDouble lambda)
 Set parameter m_lambda.
SOLVER_UTILS_EXPORT void EvaluateFunction (Array< OneD, Array< OneD, NekDouble > > &pArray, std::string pFunctionName, const NekDouble pTime=0.0, const int domain=0)
 Evaluates a function as specified in the session file.
SOLVER_UTILS_EXPORT void EvaluateFunction (std::vector< std::string > pFieldNames, Array< OneD, Array< OneD, NekDouble > > &pFields, const std::string &pName, const int domain=0)
 Populate given fields with the function from session.
SOLVER_UTILS_EXPORT void EvaluateFunction (std::vector< std::string > pFieldNames, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields, const std::string &pName, const int domain=0)
 Populate given fields with the function from session.
SOLVER_UTILS_EXPORT void EvaluateFunction (std::string pFieldName, Array< OneD, NekDouble > &pArray, const std::string &pFunctionName, const NekDouble &pTime=0.0, const int domain=0)
SOLVER_UTILS_EXPORT std::string DescribeFunction (std::string pFieldName, const std::string &pFunctionName, const int domain)
 Provide a description of a function for a given field name.
SOLVER_UTILS_EXPORT void InitialiseBaseFlow (Array< OneD, Array< OneD, NekDouble > > &base)
 Perform initialisation of the base flow.
SOLVER_UTILS_EXPORT void SetInitialConditions (NekDouble initialtime=0.0, bool dumpInitialConditions=true, const int domain=0)
 Initialise the data in the dependent fields.
SOLVER_UTILS_EXPORT void EvaluateExactSolution (int field, Array< OneD, NekDouble > &outfield, const NekDouble time)
 Evaluates an exact solution.
SOLVER_UTILS_EXPORT NekDouble L2Error (unsigned int field, const Array< OneD, NekDouble > &exactsoln, bool Normalised=false)
 Compute the L2 error between fields and a given exact solution.
SOLVER_UTILS_EXPORT NekDouble L2Error (unsigned int field, bool Normalised=false)
 Compute the L2 error of the fields.
SOLVER_UTILS_EXPORT Array
< OneD, NekDouble > 		ErrorExtraPoints (unsigned int field)
 Compute error (L2 and L_inf) over an larger set of quadrature points return [L2 Linf].
SOLVER_UTILS_EXPORT void WeakAdvectionGreensDivergenceForm (const Array< OneD, Array< OneD, NekDouble > > &F, Array< OneD, NekDouble > &outarray)
 Compute the inner product 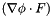$ (\nabla \phi \cdot F) $.
SOLVER_UTILS_EXPORT void WeakAdvectionDivergenceForm (const Array< OneD, Array< OneD, NekDouble > > &F, Array< OneD, NekDouble > &outarray)
 Compute the inner product 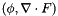$ (\phi, \nabla \cdot F) $.
SOLVER_UTILS_EXPORT void WeakAdvectionNonConservativeForm (const Array< OneD, Array< OneD, NekDouble > > &V, const Array< OneD, const NekDouble > &u, Array< OneD, NekDouble > &outarray, bool UseContCoeffs=false)
 Compute the inner product 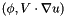$ (\phi, V\cdot \nabla u) $.
f SOLVER_UTILS_EXPORT void AdvectionNonConservativeForm (const Array< OneD, Array< OneD, NekDouble > > &V, const Array< OneD, const NekDouble > &u, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wk=NullNekDouble1DArray)
 Compute the non-conservative advection.
SOLVER_UTILS_EXPORT void WeakDGAdvection (const Array< OneD, Array< OneD, NekDouble > > &InField, Array< OneD, Array< OneD, NekDouble > > &OutField, bool NumericalFluxIncludesNormal=true, bool InFieldIsInPhysSpace=false, int nvariables=0)
 Calculate the weak discontinuous Galerkin advection.
SOLVER_UTILS_EXPORT void WeakDGDiffusion (const Array< OneD, Array< OneD, NekDouble > > &InField, Array< OneD, Array< OneD, NekDouble > > &OutField, bool NumericalFluxIncludesNormal=true, bool InFieldIsInPhysSpace=false)
 Calculate weak DG Diffusion in the LDG form.
SOLVER_UTILS_EXPORT void Checkpoint_Output (const int n)
 Write checkpoint file of m_fields.
SOLVER_UTILS_EXPORT void Checkpoint_Output (const int n, MultiRegions::ExpListSharedPtr &field, std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)
 Write checkpoint file of custom data fields.
SOLVER_UTILS_EXPORT void Checkpoint_BaseFlow (const int n)
 Write base flow file of m_fields.
SOLVER_UTILS_EXPORT void WriteFld (const std::string &outname)
 Write field data to the given filename.
SOLVER_UTILS_EXPORT void WriteFld (const std::string &outname, MultiRegions::ExpListSharedPtr &field, std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)
 Write input fields to the given filename.
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields)
 Input field data from the given file.
SOLVER_UTILS_EXPORT void ImportFldToMultiDomains (const std::string &infile, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields, const int ndomains)
 Input field data from the given file to multiple domains.
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, std::vector< std::string > &fieldStr, Array< OneD, Array< OneD, NekDouble > > &coeffs)
 Output a field. Input field data into array from the given file.
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, MultiRegions::ExpListSharedPtr &pField, std::string &pFieldName)
 Output a field. Input field data into ExpList from the given file.
SOLVER_UTILS_EXPORT void ScanForHistoryPoints ()
 Builds map of which element holds each history point.
SOLVER_UTILS_EXPORT void WriteHistoryData (std::ostream &out)
 Probe each history point and write to file.
SOLVER_UTILS_EXPORT void SessionSummary (SummaryList &vSummary)
 Write out a session summary.
SOLVER_UTILS_EXPORT Array
< OneD,
MultiRegions::ExpListSharedPtr > & 		UpdateFields ()
SOLVER_UTILS_EXPORT
LibUtilities::FieldMetaDataMap & 		UpdateFieldMetaDataMap ()
 Get hold of FieldInfoMap so it can be updated.
SOLVER_UTILS_EXPORT NekDouble GetFinalTime ()
 Return final time.
SOLVER_UTILS_EXPORT int GetNcoeffs ()
SOLVER_UTILS_EXPORT int GetNcoeffs (const int eid)
SOLVER_UTILS_EXPORT int GetNumExpModes ()
SOLVER_UTILS_EXPORT const
Array< OneD, int > 		GetNumExpModesPerExp ()
SOLVER_UTILS_EXPORT int GetNvariables ()
SOLVER_UTILS_EXPORT const
std::string 		GetVariable (unsigned int i)
SOLVER_UTILS_EXPORT int GetTraceTotPoints ()
SOLVER_UTILS_EXPORT int GetTraceNpoints ()
SOLVER_UTILS_EXPORT int GetExpSize ()
SOLVER_UTILS_EXPORT int GetPhys_Offset (int n)
SOLVER_UTILS_EXPORT int GetCoeff_Offset (int n)
SOLVER_UTILS_EXPORT int GetTotPoints ()
SOLVER_UTILS_EXPORT int GetTotPoints (int n)
SOLVER_UTILS_EXPORT int GetNpoints ()
SOLVER_UTILS_EXPORT int GetNumElmVelocity ()
SOLVER_UTILS_EXPORT int GetSteps ()
SOLVER_UTILS_EXPORT NekDouble GetTimeStep ()
SOLVER_UTILS_EXPORT void CopyFromPhysField (const int i, Array< OneD, NekDouble > &output)
SOLVER_UTILS_EXPORT void CopyToPhysField (const int i, Array< OneD, NekDouble > &output)
SOLVER_UTILS_EXPORT void SetStepsToOne ()
SOLVER_UTILS_EXPORT void ZeroPhysFields ()
SOLVER_UTILS_EXPORT void FwdTransFields ()
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &flux)
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &fluxX, Array< OneD, Array< OneD, NekDouble > > &fluxY)
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, const int j, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &flux)
SOLVER_UTILS_EXPORT void NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numflux)
SOLVER_UTILS_EXPORT void NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numfluxX, Array< OneD, Array< OneD, NekDouble > > &numfluxY)
SOLVER_UTILS_EXPORT void NumFluxforScalar (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &uflux)
SOLVER_UTILS_EXPORT void NumFluxforVector (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &qfield, Array< OneD, Array< OneD, NekDouble > > &qflux)
SOLVER_UTILS_EXPORT void SetModifiedBasis (const bool modbasis)
SOLVER_UTILS_EXPORT int NoCaseStringCompare (const string &s1, const string &s2)
 Perform a case-insensitive string comparison.

Static Public Member Functions

static
SolverUtils::EquationSystemSharedPtr 		create (const LibUtilities::SessionReaderSharedPtr &pSession)
 Creates an instance of this class.

Public Attributes

Array< OneD, Array< OneD,
NekDouble > > 		m_ForcingTerm
Array< OneD, Array< OneD,
NekDouble > > 		m_ForcingTerm_Coeffs
Array< OneD,
CoupledLocalToGlobalC0ContMapSharedPtr > 		m_locToGloMap

Static Public Attributes

static std::string className = SolverUtils::GetEquationSystemFactory().RegisterCreatorFunction("CoupledLinearisedNS", CoupledLinearNS::create)
 Name of class.

Protected Member Functions

 CoupledLinearNS (const LibUtilities::SessionReaderSharedPtr &pSesssion)
virtual void v_InitObject ()
 Init object for UnsteadySystem class.
- Protected Member Functions inherited from Nektar::IncNavierStokes
 IncNavierStokes (const LibUtilities::SessionReaderSharedPtr &pSession)
 Constructor.
EquationType GetEquationType (void)
void EvaluateAdvectionTerms (const Array< OneD, const Array< OneD, NekDouble > > &inarray, Array< OneD, Array< OneD, NekDouble > > &outarray, Array< OneD, NekDouble > &wk=NullNekDouble1DArray)
void WriteModalEnergy (void)
void SetBoundaryConditions (NekDouble time)
 time dependent boundary conditions updating
void SetRadiationBoundaryForcing (int fieldid)
 Set Radiation forcing term.
bool CalcSteadyState (void)
 evaluate steady state
virtual
MultiRegions::ExpListSharedPtr 		v_GetPressure ()
virtual void v_TransCoeffToPhys (void)
 Virtual function for transformation to physical space.
virtual void v_TransPhysToCoeff (void)
 Virtual function for transformation to coefficient space.
virtual int v_GetForceDimension ()=0
virtual bool v_PreIntegrate (int step)
virtual bool v_PostIntegrate (int step)

Private Member Functions

void SetUpCoupledMatrix (const NekDouble lambda, const Array< OneD, Array< OneD, NekDouble > > &Advfield, bool IsLinearNSEquation, const int HomogeneousMode, CoupledSolverMatrices &mat, CoupledLocalToGlobalC0ContMapSharedPtr &locToGloMap, const NekDouble lambda_imag=NekConstants::kNekUnsetDouble)
virtual void v_GenerateSummary (SolverUtils::SummaryList &s)
virtual void v_DoInitialise (void)
virtual void v_DoSolve (void)
virtual void v_TransCoeffToPhys (void)
virtual void v_TransPhysToCoeff (void)
virtual void v_Output (void)
virtual int v_GetForceDimension (void)

Private Attributes

bool m_singleMode
 Identify if a single mode is required for stability analysis.
bool m_zeroMode
 Id to identify when single mode is mean mode (i.e. beta=0);.
int m_counter
bool m_initialStep
NekDouble m_tol
int m_maxIt
int m_Restart
int m_MatrixSetUpStep
NekDouble m_kinvisMin
NekDouble m_kinvisStep
NekDouble m_KinvisPercentage
Array< OneD,
CoupledSolverMatrices > 		m_mat

Friends

class MemoryManager< CoupledLinearNS >

Additional Inherited Members

- Protected Types inherited from Nektar::SolverUtils::EquationSystem
enum  HomogeneousType { eHomogeneous1D, eHomogeneous2D, eHomogeneous3D, eNotHomogeneous }
 Parameter for homogeneous expansions. More...
- Protected Attributes inherited from Nektar::IncNavierStokes
ExtrapolateSharedPtr m_extrapolation
std::ofstream m_mdlFile
 modal energy file
bool m_subSteppingScheme
 bool to identify if using a substepping scheme
bool m_SmoothAdvection
 bool to identify if advection term smoothing is requested
LibUtilities::TimeIntegrationWrapperSharedPtr m_subStepIntegrationScheme
std::vector
< SolverUtils::ForcingSharedPtr > 		m_forcing
 Forcing terms.
int m_nConvectiveFields
 Number of fields to be convected;.
Array< OneD, int > m_velocity
 int which identifies which components of m_fields contains the velocity (u,v,w);
MultiRegions::ExpListSharedPtr m_pressure
 Pointer to field holding pressure field.
NekDouble m_kinvis
 Kinematic viscosity.
int m_energysteps
 dump energy to file at steps time
int m_cflsteps
 dump cfl estimate
int m_steadyStateSteps
 Check for steady state at step interval.
NekDouble m_steadyStateTol
 Tolerance to which steady state should be evaluated at.
EquationType m_equationType
 equation type;
Array< OneD, Array< OneD, int > > m_fieldsBCToElmtID
 Mapping from BCs to Elmt IDs.
Array< OneD, Array< OneD, int > > m_fieldsBCToTraceID
 Mapping from BCs to Elmt Edge IDs.
Array< OneD, Array< OneD,
NekDouble > > 		m_fieldsRadiationFactor
 RHS Factor for Radiation Condition.
int m_intSteps
 Number of time integration steps AND Order of extrapolation for pressure boundary conditions.

Detailed Description

Set up expansion field for velocity and pressure, the local to global mapping arrays and the basic memory definitions for coupled matrix system

Definition at line 89 of file CoupledLinearNS.h.

Constructor & Destructor Documentation

Nektar::CoupledLinearNS::CoupledLinearNS ( const LibUtilities::SessionReaderSharedPtr &  pSesssion)
protected

Definition at line 57 of file CoupledLinearNS.cpp.

:
UnsteadySystem(pSession),
IncNavierStokes(pSession),
m_singleMode(false),
m_zeroMode(false)
{
}

Member Function Documentation

void Nektar::CoupledLinearNS::Continuation ( void  )

Definition at line 1653 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::m_fields, Nektar::IncNavierStokes::m_kinvis, m_KinvisPercentage, Nektar::IncNavierStokes::m_velocity, SetUpCoupledMatrix(), Vmath::Smul(), SolveLinearNS(), and Vmath::Vadd().

Referenced by v_DoSolve().

{
Array<OneD, Array<OneD, NekDouble> > u_N(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > tmp_RHS(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > RHS(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > u_star(m_velocity.num_elements());
cout << "We apply the continuation method: " <<endl;
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
u_N[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
m_fields[m_velocity[i]]->BwdTrans_IterPerExp(m_fields[m_velocity[i]]->GetCoeffs(), u_N[i]);
RHS[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
tmp_RHS[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
m_fields[m_velocity[i]]->PhysDeriv(i, u_N[i], tmp_RHS[i]);
Vmath::Smul(tmp_RHS[i].num_elements(), m_kinvis, tmp_RHS[i], 1, tmp_RHS[i], 1);
m_fields[m_velocity[i]]->IProductWRTDerivBase(i, tmp_RHS[i], RHS[i]);
}
SetUpCoupledMatrix(0.0, u_N, true);
SolveLinearNS(RHS);
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
u_star[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
m_fields[m_velocity[i]]->BwdTrans_IterPerExp(m_fields[m_velocity[i]]->GetCoeffs(), u_star[i]);
//u_star(k+1) = u_N(k) + DeltaKinvis * u_star(k)
Vmath::Smul(u_star[i].num_elements(), m_kinvis, u_star[i], 1, u_star[i], 1);
Vmath::Vadd(u_star[i].num_elements(), u_star[i], 1, u_N[i], 1, u_star[i], 1);
m_fields[m_velocity[i]]->FwdTrans(u_star[i], m_fields[m_velocity[i]]->UpdateCoeffs());
}
m_kinvis -= m_kinvis*m_KinvisPercentage/100;
}
static SolverUtils::EquationSystemSharedPtr Nektar::CoupledLinearNS::create ( const LibUtilities::SessionReaderSharedPtr &  pSession)
inlinestatic

Creates an instance of this class.

Definition at line 95 of file CoupledLinearNS.h.

{
SolverUtils::EquationSystemSharedPtr p = MemoryManager<CoupledLinearNS>::AllocateSharedPtr(pSession);
p->InitObject();
return p;
}
void Nektar::CoupledLinearNS::DefineForcingTerm ( void  )

Definition at line 1528 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::EvaluateFunction(), Nektar::SolverUtils::EquationSystem::m_boundaryConditions, Nektar::SolverUtils::EquationSystem::m_fields, m_ForcingTerm, m_ForcingTerm_Coeffs, Nektar::SolverUtils::EquationSystem::m_session, and Nektar::IncNavierStokes::m_velocity.

Referenced by v_DoInitialise().

{
m_ForcingTerm = Array<OneD, Array<OneD, NekDouble> > (m_velocity.num_elements());
m_ForcingTerm_Coeffs = Array<OneD, Array<OneD, NekDouble> > (m_velocity.num_elements());
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
m_ForcingTerm[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
m_ForcingTerm_Coeffs[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetNcoeffs(),0.0);
}
if(m_session->DefinesFunction("ForcingTerm"))
{
std::vector<std::string> fieldStr;
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
fieldStr.push_back(m_boundaryConditions->GetVariable(m_velocity[i]));
}
EvaluateFunction(fieldStr, m_ForcingTerm, "ForcingTerm");
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->FwdTrans_IterPerExp(m_ForcingTerm[i], m_ForcingTerm_Coeffs[i]);
}
}
else
{
cout << "'ForcingTerm' section has not been defined in the input file => forcing=0" << endl;
}
}
void Nektar::CoupledLinearNS::EvaluateAdvection ( const Array< OneD, const Array< OneD, NekDouble > > &  inarray,
Array< OneD, Array< OneD, NekDouble > > &  outarray,
const NekDouble  time 
)

Definition at line 1353 of file CoupledLinearNS.cpp.

References Nektar::IncNavierStokes::EvaluateAdvectionTerms(), Nektar::SolverUtils::EquationSystem::m_fields, and Nektar::IncNavierStokes::m_forcing.

Referenced by v_DoInitialise().

{
// evaluate convectioln terms
EvaluateAdvectionTerms(inarray,outarray);
std::vector<SolverUtils::ForcingSharedPtr>::const_iterator x;
for (x = m_forcing.begin(); x != m_forcing.end(); ++x)
{
(*x)->Apply(m_fields, outarray, outarray, time);
}
}
void Nektar::CoupledLinearNS::EvaluateNewtonRHS ( Array< OneD, Array< OneD, NekDouble > > &  Velocity,
Array< OneD, Array< OneD, NekDouble > > &  outarray 
)

Definition at line 1728 of file CoupledLinearNS.cpp.

References Nektar::IncNavierStokes::EvaluateAdvectionTerms(), Nektar::SolverUtils::EquationSystem::m_fields, m_ForcingTerm, Nektar::IncNavierStokes::m_kinvis, Nektar::IncNavierStokes::m_velocity, Vmath::Smul(), Vmath::Vadd(), and Vmath::Vsub().

Referenced by SolveSteadyNavierStokes().

{
Array<OneD, Array<OneD, NekDouble> > Eval_Adv(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > tmp_DerVel(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > AdvTerm(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > ViscTerm(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > Forc(m_velocity.num_elements());
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
Eval_Adv[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
tmp_DerVel[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
AdvTerm[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
ViscTerm[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
Forc[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
outarray[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
m_fields[m_velocity[i]]->PhysDeriv(i, Velocity[i], tmp_DerVel[i]);
Vmath::Smul(tmp_DerVel[i].num_elements(), m_kinvis, tmp_DerVel[i], 1, tmp_DerVel[i], 1);
}
EvaluateAdvectionTerms(Velocity, Eval_Adv);
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->IProductWRTBase(Eval_Adv[i], AdvTerm[i]); //(w, (u.grad)u)
m_fields[m_velocity[i]]->IProductWRTDerivBase(i, tmp_DerVel[i], ViscTerm[i]); //(grad w, grad u)
m_fields[m_velocity[i]]->IProductWRTBase(m_ForcingTerm[i], Forc[i]); //(w, f)
Vmath::Vsub(outarray[i].num_elements(), outarray[i], 1, AdvTerm[i], 1, outarray[i], 1);
Vmath::Vsub(outarray[i].num_elements(), outarray[i], 1, ViscTerm[i], 1, outarray[i], 1);
Vmath::Vadd(outarray[i].num_elements(), outarray[i], 1, Forc[i], 1, outarray[i], 1);
}
}
const SpatialDomains::ExpansionMap & Nektar::CoupledLinearNS::GenPressureExp ( const SpatialDomains::ExpansionMap &  VelExp)

Definition at line 1769 of file CoupledLinearNS.cpp.

References ASSERTL0, Nektar::LibUtilities::BasisKey::GetBasisType(), Nektar::LibUtilities::BasisKey::GetNumModes(), Nektar::LibUtilities::BasisKey::GetPointsKey(), and Nektar::SolverUtils::EquationSystem::m_graph.

Referenced by v_InitObject().

{
int i;
SpatialDomains::ExpansionMapShPtr returnval;
returnval = MemoryManager<SpatialDomains::ExpansionMap>::AllocateSharedPtr();
SpatialDomains::ExpansionMap::const_iterator expMapIter;
int nummodes;
for (expMapIter = VelExp.begin(); expMapIter != VelExp.end(); ++expMapIter)
{
LibUtilities::BasisKeyVector BasisVec;
for(i = 0; i < expMapIter->second->m_basisKeyVector.size(); ++i)
{
LibUtilities::BasisKey B = expMapIter->second->m_basisKeyVector[i];
nummodes = B.GetNumModes();
ASSERTL0(nummodes > 3,"Velocity polynomial space not sufficiently high (>= 4)");
// Should probably set to be an orthogonal basis.
LibUtilities::BasisKey newB(B.GetBasisType(),nummodes-2,B.GetPointsKey());
BasisVec.push_back(newB);
}
// Put new expansion into list.
SpatialDomains::ExpansionShPtr expansionElementShPtr =
MemoryManager<SpatialDomains::Expansion>::AllocateSharedPtr(expMapIter->second->m_geomShPtr, BasisVec);
(*returnval)[expMapIter->first] = expansionElementShPtr;
}
// Save expansion into graph.
m_graph->SetExpansions("p",returnval);
return *returnval;
}
void Nektar::CoupledLinearNS::InfNorm ( Array< OneD, Array< OneD, NekDouble > > &  inarray,
Array< OneD, NekDouble > &  outarray 
)

Definition at line 1695 of file CoupledLinearNS.cpp.

References Nektar::IncNavierStokes::m_velocity.

{
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
outarray[i] = 0.0;
for(int j = 0; j < inarray[i].num_elements(); ++j)
{
if(inarray[i][j] > outarray[i])
{
outarray[i] = inarray[i][j];
}
}
cout << "InfNorm["<<i<<"] = "<< outarray[i] <<endl;
}
}
void Nektar::CoupledLinearNS::L2Norm ( Array< OneD, Array< OneD, NekDouble > > &  inarray,
Array< OneD, NekDouble > &  outarray 
)

Definition at line 1712 of file CoupledLinearNS.cpp.

References Nektar::IncNavierStokes::m_velocity.

Referenced by SolveSteadyNavierStokes().

{
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
outarray[i] = 0.0;
for(int j = 0; j < inarray[i].num_elements(); ++j)
{
outarray[i] += inarray[i][j]*inarray[i][j];
}
outarray[i]=sqrt(outarray[i]);
cout << "L2Norm["<<i<<"] = "<< outarray[i] <<endl;
}
}
void Nektar::CoupledLinearNS::SetUpCoupledMatrix ( const NekDouble  lambda = 0.0,
const Array< OneD, Array< OneD, NekDouble > > &  Advfield = NullNekDoubleArrayofArray,
bool  IsLinearNSEquation = true 
)

Generate the linearised Navier Stokes solver based on the static condensation of the interior velocity space and pressure modes.

Set up a coupled linearised Naviers-Stokes solve. Primarily a wrapper fuction around the full mode by mode version of SetUpCoupledMatrix.

Definition at line 180 of file CoupledLinearNS.cpp.

References ASSERTL1, Nektar::NekConstants::kNekUnsetDouble, Nektar::IncNavierStokes::m_kinvis, Nektar::SolverUtils::EquationSystem::m_LhomZ, m_locToGloMap, m_mat, Nektar::SolverUtils::EquationSystem::m_npointsZ, Nektar::SolverUtils::EquationSystem::m_session, m_singleMode, and m_zeroMode.

Referenced by Continuation(), SolveSteadyNavierStokes(), SolveUnsteadyStokesSystem(), and v_DoInitialise().

{
int nz;
if(m_singleMode)
{
NekDouble lambda_imag;
// load imaginary componont of any potential shift
// Probably should be called from DriverArpack but not yet
// clear how to do this
m_session->LoadParameter("imagShift",lambda_imag,NekConstants::kNekUnsetDouble);
nz = 1;
m_mat = Array<OneD, CoupledSolverMatrices> (nz);
ASSERTL1(m_npointsZ <=2,"Only expected a maxmimum of two planes in single mode linear NS solver");
if(m_zeroMode)
{
SetUpCoupledMatrix(lambda,Advfield,IsLinearNSEquation,0,m_mat[0],m_locToGloMap[0],lambda_imag);
}
else
{
NekDouble beta = 2*M_PI/m_LhomZ;
NekDouble lam = lambda + m_kinvis*beta*beta;
SetUpCoupledMatrix(lam,Advfield,IsLinearNSEquation,1,m_mat[0],m_locToGloMap[0],lambda_imag);
}
}
else
{
int n;
if(m_npointsZ > 1)
{
nz = m_npointsZ/2;
}
else
{
nz = 1;
}
m_mat = Array<OneD, CoupledSolverMatrices> (nz);
// mean mode or 2D mode.
SetUpCoupledMatrix(lambda,Advfield,IsLinearNSEquation,0,m_mat[0],m_locToGloMap[0]);
for(n = 1; n < nz; ++n)
{
NekDouble beta = 2*M_PI*n/m_LhomZ;
NekDouble lam = lambda + m_kinvis*beta*beta;
SetUpCoupledMatrix(lam,Advfield,IsLinearNSEquation,n,m_mat[n],m_locToGloMap[n]);
}
}
}
void Nektar::CoupledLinearNS::SetUpCoupledMatrix ( const NekDouble  lambda,
const Array< OneD, Array< OneD, NekDouble > > &  Advfield,
bool  IsLinearNSEquation,
const int  HomogeneousMode,
CoupledSolverMatrices &  mat,
CoupledLocalToGlobalC0ContMapSharedPtr &  locToGloMap,
const NekDouble  lambda_imag = NekConstants::kNekUnsetDouble 
)
private

Generate the linearised Navier Stokes solver based on the static condensation of the interior velocity space and pressure modes. This call also allows for a Fourier mode to be specified, however if HomogeneneousMode= 0 then can be used for a standared 2D and hopefully 3D (in the future).

Set up a coupled linearised Naviers-Stokes solve in the following manner:

Consider the linearised Navier-Stokes element matrix denoted as

\[ \left [ \begin{array}{ccc} A & -D_{bnd}^T & B\\ -D_{bnd}& 0 & -D_{int}\\ \tilde{B}^T & -D_{int}^T & C \end{array} \right ] \left [ \begin{array}{c} {\bf v}_{bnd} \\ p\\ {\bf v}_{int} \end{array} \right ] = \left [ \begin{array}{c} {\bf f}_{bnd} \\ 0\\ {\bf f}_{int} \end{array} \right ] \]

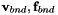where ${\bf v}_{bnd}, {\bf f}_{bnd}$ denote the degrees of freedom of the elemental velocities on the boundary of the element, 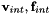${\bf v}_{int}, {\bf f}_{int}$ denote the degrees of freedom of the elemental velocities on the interior of the element and 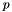$p$ is the piecewise continuous pressure. The matrices have the interpretation

\[ A[n,m] = (\nabla \phi^b_n, \nu \nabla \phi^b_m) + (\phi^b_n,{\bf U \cdot \nabla} \phi^b_m) + (\phi^b_n \nabla^T {\bf U} \phi^b_m), \]

\[ B[n,m] = (\nabla \phi^b_n, \nu \nabla \phi^i_m) + (\phi^b_n,{\bf U \cdot \nabla} \phi^i_m) + (\phi^b_n \nabla^T {\bf U} \phi^i_m),\]

\[\tilde{B}^T[n,m] = (\nabla \phi^i_n, \nu \nabla \phi^b_m) + (\phi^i_n,{\bf U \cdot \nabla} \phi^b_m) + (\phi^i_n \nabla^T {\bf U} \phi^b_m) \]

\[ C[n,m] = (\nabla \phi^i_n, \nu \nabla \phi^i_m) + (\phi^i_n,{\bf U \cdot \nabla} \phi^i_m) + (\phi^i_n \nabla^T {\bf U} \phi^i_m),\]

\[ D_{bnd}[n,m] = (\psi_m,\nabla \phi^b),\]

\[ D_{int}[n,m] = (\psi_m,\nabla \phi^i) \]

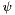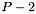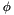where $\psi$ is the space of pressures typically at order $P-2$ and $\phi$ is the velocity vector space of polynomial order 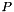$P$. (Note the above definitions for the transpose terms shoudl be interpreted with care since we have used a tensor differential for the 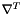$\nabla^T $ terms)

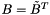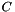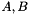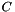Note $B = \tilde{B}^T$ if just considering the stokes operator and then $C$ is also symmetric. Also note that $A,B$ and $C$ are block diagonal in the Oseen equation when 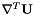$\nabla^T {\bf U}$ are zero.

Since 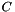$C$ is invertible we can premultiply the governing elemental equation by the following matrix:

\[ \left [ \begin{array}{ccc} I & 0 & -BC^{-1}\\ 0& I & D_{int}C^{-1}\\ 0 & 0 & I \end{array} \right ] \left \{ \left [ \begin{array}{ccc} A & -D_{bnd}^T & B\\ -D_{bnd}& 0 & -D_{int}\\ \tilde{B}^T & -D_{int}^T & C \end{array} \right ] \left [ \begin{array}{c} {\bf v}_{bnd} \\ p\\ {\bf v_{int}} \end{array} \right ] = \left [ \begin{array}{c} {\bf f}_{bnd} \\ 0\\ {\bf f_{int}} \end{array} \right ] \right \} \]

which if we multiply out the matrix equation we obtain

\[ \left [ \begin{array}{ccc} A - B C^{-1}\tilde{B}^T & -D_{bnd}^T +B C^{-1} D_{int}^T& 0\\ -D_{bnd}+D_{int} C^{-1} \tilde{B}^T & -D_{int} C^{-1} D_{int}^T & 0\\ \tilde{B}^T & -D_{int}^T & C \end{array} \right ] \left [ \begin{array}{c} {\bf v}_{bnd} \\ p\\ {\bf v_{int}} \end{array} \right ] = \left [ \begin{array}{c} {\bf f}_{bnd} -B C^{-1} {\bf f}_{int}\\ f_p = D_{int} C^{-1} {\bf f}_{int}\\ {\bf f_{int}} \end{array} \right ] \]

In the above equation the 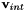${\bf v}_{int}$ degrees of freedom are decoupled and so we need to solve for the 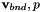${\bf v}_{bnd}, p$ degrees of freedom. The final step is to perform a second level of static condensation but where we will lump the mean pressure mode (or a pressure degree of freedom containing a mean component) with the velocity boundary degrees of freedom. 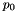To do we define ${\bf b} = [{\bf v}_{bnd}, p_0]$ where $p_0$ is the mean pressure mode and 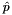$\hat{p}$ to be the remainder of the pressure space. We now repartition the top 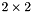$2 \times 2$ block of matrices of previous matrix equation as

\[ \left [ \begin{array}{cc} \hat{A} & \hat{B}\\ \hat{C} & \hat{D} \end{array} \right ] \left [ \begin{array}{c} {\bf b} \\ \hat{p} \end{array} \right ] = \left [ \begin{array}{c} \hat{\bf f}_{bnd} \\ \hat{f}_p \end{array} \right ] \label{eqn.linNS_fac2} \]

where

\[ \hat{A}_{ij} = \left [ \begin{array}{cc} A - B C^{-1}\tilde{B}^T & [-D_{bnd}^T +B C^{-1} D_{int}^T]_{i0}\\ {[}-D_{bnd}+D_{int} C^{-1} \tilde{B}^T]_{0j} & -[D_{int} C^{-1} D_{int}^T ]_{00} \end{array} \right ] \]

\[ \hat{B}_{ij} = \left [ \begin{array}{c} [-D_{bnd}^T +B C^{-1} D_{int}^T]_{i,j+1} \\ {[} -D_{int} C^{-1} D^T_{int} ]_{0j}\end{array} \right ] \]

\[ \hat{C}_{ij} = \left [\begin{array}{cc} -D_{bnd} + D_{int} C^{-1} \tilde{B}^T, & {[} -D_{int} C^{-1} D^T_{int} ]_{i+1,0}\end{array} \right ] \]

\[ \hat{D}_{ij} = \left [\begin{array}{c} {[} -D_{int} C^{-1} D^T_{int} ]_{i+1,j+1}\end{array} \right ] \]

and

\[ fh\_{bnd} = \left [ \begin{array}{c} {\bf f}_{bnd} -B C^{-1} {\bf f}_{int}\\ {[}D_{int} C^{-1} {\bf f}_{int}]_0 \end{array}\right ] \hspace{1cm} [fh\_p_{i} = \left [ \begin{array}{c} {[}D_{int} C^{-1} {\bf f}_{iint}]_{i+1} \end{array}\right ] \]

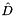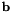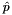Since the $\hat{D}$ is decoupled and invertible we can now statically condense the previous matrix equationto decouple ${\bf b}$ from $\hat{p}$ by solving the following system

\[ \left [ \begin{array}{cc} \hat{A} - \hat{B} \hat{D}^{-1} \hat{C} & 0 \\ \hat{C} & \hat{D} \end{array} \right ] \left [ \begin{array}{c} {\bf b} \\ \hat{p} \end{array} \right ] = \left [ \begin{array}{c} \hat{\bf f}_{bnd} - \hat{B} \hat{D}^{-1} \hat{f}_p\\ \hat{f}_p \end{array} \right ] \]

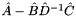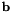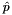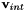The matrix $\hat{A} - \hat{B} \hat{D}^{-1} \hat{C}$ has to be globally assembled and solved iteratively or directly. One we obtain the solution to ${\bf b}$ we can use the second row of equation fourth matrix equation to solve for $\hat{p}$ and finally the last row of equation second matrix equation to solve for ${\bf v}_{int}$.

Definition at line 377 of file CoupledLinearNS.cpp.

References Nektar::MultiRegions::DirCartesianMap, Nektar::eDIAGONAL, Nektar::StdRegions::eFactorLambda, Nektar::StdRegions::eHelmholtz, Nektar::SolverUtils::EquationSystem::eHomogeneous1D, Nektar::StdRegions::eLinearAdvectionReaction, Nektar::StdRegions::eMass, Nektar::SolverUtils::EquationSystem::GetTotPoints(), Nektar::NekConstants::kNekUnsetDouble, Nektar::coupledSolverMatrices::m_BCinv, Nektar::coupledSolverMatrices::m_Btilde, Nektar::coupledSolverMatrices::m_Cinv, Nektar::coupledSolverMatrices::m_CoupledBndSys, Nektar::coupledSolverMatrices::m_D_bnd, Nektar::coupledSolverMatrices::m_D_int, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_HomogeneousType, Nektar::IncNavierStokes::m_kinvis, Nektar::SolverUtils::EquationSystem::m_LhomZ, Nektar::IncNavierStokes::m_pressure, m_singleMode, Nektar::IncNavierStokes::m_velocity, Vmath::Neg(), Nektar::NullNekDoubleArrayofArray, Vmath::Smul(), Nektar::Timer::Start(), Nektar::Timer::Stop(), Nektar::Timer::TimePerTest(), Nektar::Transpose(), Vmath::Vmul(), and Vmath::Zero().

{
int n,i,j,k,eid;
int nel = m_fields[m_velocity[0]]->GetNumElmts();
int nvel = m_velocity.num_elements();
// if Advfield is defined can assume it is an Oseen or LinearNS equation
bool AddAdvectionTerms = (Advfield == NullNekDoubleArrayofArray)? false: true;
//bool AddAdvectionTerms = true; // Temporary debugging trip
// call velocity space Static condensation and fill block
// matrices. Need to set this up differently for Oseen and
// Lin NS. Ideally should make block diagonal for Stokes and
// Oseen problems.
DNekScalMatSharedPtr loc_mat;
StdRegions::StdExpansionSharedPtr locExp;
NekDouble one = 1.0;
int nint,nbndry;
int rows, cols;
NekDouble zero = 0.0;
Array<OneD, unsigned int> bmap,imap;
Array<OneD,unsigned int> nsize_bndry (nel);
Array<OneD,unsigned int> nsize_bndry_p1(nel);
Array<OneD,unsigned int> nsize_int (nel);
Array<OneD,unsigned int> nsize_p (nel);
Array<OneD,unsigned int> nsize_p_m1 (nel);
int nz_loc;
if(HomogeneousMode) // Homogeneous mode flag
{
nz_loc = 2;
}
else
{
if(m_singleMode)
{
nz_loc = 2;
}
else
{
nz_loc = 1;
}
}
// Set up block matrix sizes -
for(n = 0; n < nel; ++n)
{
eid = m_fields[m_velocity[0]]->GetOffset_Elmt_Id(n);
nsize_bndry[n] = nvel*m_fields[m_velocity[0]]->GetExp(eid)->NumBndryCoeffs()*nz_loc;
nsize_bndry_p1[n] = nsize_bndry[n]+nz_loc;
nsize_int [n] = (nvel*m_fields[m_velocity[0]]->GetExp(eid)->GetNcoeffs()*nz_loc - nsize_bndry[n]);
nsize_p[n] = m_pressure->GetExp(eid)->GetNcoeffs()*nz_loc;
nsize_p_m1[n] = nsize_p[n]-nz_loc;
}
MatrixStorage blkmatStorage = eDIAGONAL;
DNekScalBlkMatSharedPtr pAh = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_bndry_p1,nsize_bndry_p1,blkmatStorage);
mat.m_BCinv = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_bndry,nsize_int,blkmatStorage);
mat.m_Btilde = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_bndry,nsize_int,blkmatStorage);
mat.m_Cinv = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_int,nsize_int,blkmatStorage);
mat.m_D_bnd = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_p,nsize_bndry,blkmatStorage);
mat.m_D_int = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_p,nsize_int,blkmatStorage);
// Final level static condensation matrices.
DNekScalBlkMatSharedPtr pBh = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_bndry_p1,nsize_p_m1,blkmatStorage);
DNekScalBlkMatSharedPtr pCh = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_p_m1,nsize_bndry_p1,blkmatStorage);
DNekScalBlkMatSharedPtr pDh = MemoryManager<DNekScalBlkMat>
::AllocateSharedPtr(nsize_p_m1,nsize_p_m1,blkmatStorage);
Timer timer;
timer.Start();
for(n = 0; n < nel; ++n)
{
eid = m_fields[m_velocity[0]]->GetOffset_Elmt_Id(n);
nbndry = nsize_bndry[n];
nint = nsize_int[n];
k = nsize_bndry_p1[n];
DNekMatSharedPtr Ah = MemoryManager<DNekMat>::AllocateSharedPtr(k,k,zero);
Array<OneD, NekDouble> Ah_data = Ah->GetPtr();
int AhRows = k;
DNekMatSharedPtr B = MemoryManager<DNekMat>::AllocateSharedPtr(nbndry,nint,zero);
Array<OneD, NekDouble> B_data = B->GetPtr();
DNekMatSharedPtr C = MemoryManager<DNekMat>::AllocateSharedPtr(nbndry,nint,zero);
Array<OneD, NekDouble> C_data = C->GetPtr();
DNekMatSharedPtr D = MemoryManager<DNekMat>::AllocateSharedPtr(nint, nint,zero);
Array<OneD, NekDouble> D_data = D->GetPtr();
DNekMatSharedPtr Dbnd = MemoryManager<DNekMat>::AllocateSharedPtr(nsize_p[n],nsize_bndry[n],zero);
DNekMatSharedPtr Dint = MemoryManager<DNekMat>::AllocateSharedPtr(nsize_p[n],nsize_int[n],zero);
locExp = m_fields[m_velocity[0]]->GetExp(eid);
locExp->GetBoundaryMap(bmap);
locExp->GetInteriorMap(imap);
StdRegions::ConstFactorMap factors;
factors[StdRegions::eFactorLambda] = lambda/m_kinvis;
LocalRegions::MatrixKey helmkey(StdRegions::eHelmholtz,
locExp->DetShapeType(),
*locExp,
factors);
int ncoeffs = m_fields[m_velocity[0]]->GetExp(eid)->GetNcoeffs();
int nphys = m_fields[m_velocity[0]]->GetExp(eid)->GetTotPoints();
int nbmap = bmap.num_elements();
int nimap = imap.num_elements();
Array<OneD, NekDouble> coeffs(ncoeffs);
Array<OneD, NekDouble> phys (nphys);
int psize = m_pressure->GetExp(eid)->GetNcoeffs();
int pqsize = m_pressure->GetExp(eid)->GetTotPoints();
Array<OneD, NekDouble> deriv (pqsize);
Array<OneD, NekDouble> pcoeffs(psize);
if(AddAdvectionTerms == false) // use static condensed managed matrices
{
// construct velocity matrices using statically
// condensed elemental matrices and then construct
// pressure matrix systems
DNekScalBlkMatSharedPtr CondMat;
CondMat = locExp->GetLocStaticCondMatrix(helmkey);
for(k = 0; k < nvel*nz_loc; ++k)
{
DNekScalMat &SubBlock = *CondMat->GetBlock(0,0);
rows = SubBlock.GetRows();
cols = SubBlock.GetColumns();
for(i = 0; i < rows; ++i)
{
for(j = 0; j < cols; ++j)
{
(*Ah)(i+k*rows,j+k*cols) = m_kinvis*SubBlock(i,j);
}
}
}
for(k = 0; k < nvel*nz_loc; ++k)
{
DNekScalMat &SubBlock = *CondMat->GetBlock(0,1);
DNekScalMat &SubBlock1 = *CondMat->GetBlock(1,0);
rows = SubBlock.GetRows();
cols = SubBlock.GetColumns();
for(i = 0; i < rows; ++i)
{
for(j = 0; j < cols; ++j)
{
(*B)(i+k*rows,j+k*cols) = SubBlock(i,j);
(*C)(i+k*rows,j+k*cols) = m_kinvis*SubBlock1(j,i);
}
}
}
for(k = 0; k < nvel*nz_loc; ++k)
{
DNekScalMat &SubBlock = *CondMat->GetBlock(1,1);
NekDouble inv_kinvis = 1.0/m_kinvis;
rows = SubBlock.GetRows();
cols = SubBlock.GetColumns();
for(i = 0; i < rows; ++i)
{
for(j = 0; j < cols; ++j)
{
(*D)(i+k*rows,j+k*cols) = inv_kinvis*SubBlock(i,j);
}
}
}
// Loop over pressure space and construct boundary block matrices.
for(i = 0; i < bmap.num_elements(); ++i)
{
// Fill element with mode
Vmath::Zero(ncoeffs,coeffs,1);
coeffs[bmap[i]] = 1.0;
m_fields[m_velocity[0]]->GetExp(eid)->BwdTrans(coeffs,phys);
// Differentiation & Inner product wrt base.
for(j = 0; j < nvel; ++j)
{
if( (nz_loc == 2)&&(j == 2)) // handle d/dz derivative
{
NekDouble beta = -2*M_PI*HomogeneousMode/m_LhomZ;
Vmath::Smul(m_fields[m_velocity[0]]->GetExp(eid)->GetTotPoints(), beta, phys,1,deriv,1);
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dbnd->GetRawPtr() +
((nz_loc*j+1)*bmap.num_elements()+i)*nsize_p[n],1);
Vmath::Neg(psize,pcoeffs,1);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dbnd->GetRawPtr() +
((nz_loc*j)*bmap.num_elements()+i)*nsize_p[n]+psize,1);
}
else
{
if(j < 2) // required for mean mode of homogeneous expansion
{
locExp->PhysDeriv(MultiRegions::DirCartesianMap[j],phys,deriv);
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
// copy into column major storage.
for(k = 0; k < nz_loc; ++k)
{
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dbnd->GetRawPtr() +
((nz_loc*j+k)*bmap.num_elements()+i)*nsize_p[n]+ k*psize,1);
}
}
}
}
}
for(i = 0; i < imap.num_elements(); ++i)
{
// Fill element with mode
Vmath::Zero(ncoeffs,coeffs,1);
coeffs[imap[i]] = 1.0;
m_fields[m_velocity[0]]->GetExp(eid)->BwdTrans(coeffs,phys);
// Differentiation & Inner product wrt base.
for(j = 0; j < nvel; ++j)
{
if( (nz_loc == 2)&&(j == 2)) // handle d/dz derivative
{
NekDouble beta = -2*M_PI*HomogeneousMode/m_LhomZ;
Vmath::Smul(m_fields[m_velocity[0]]->GetExp(eid)->GetTotPoints(), beta, phys,1,deriv,1);
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dint->GetRawPtr() +
((nz_loc*j+1)*imap.num_elements()+i)*nsize_p[n],1);
Vmath::Neg(psize,pcoeffs,1);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dint->GetRawPtr() +
((nz_loc*j)*imap.num_elements()+i)*nsize_p[n]+psize,1);
}
else
{
if(j < 2) // required for mean mode of homogeneous expansion
{
//m_fields[m_velocity[0]]->GetExp(eid)->PhysDeriv(j,phys, deriv);
locExp->PhysDeriv(MultiRegions::DirCartesianMap[j],phys,deriv);
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
// copy into column major storage.
for(k = 0; k < nz_loc; ++k)
{
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dint->GetRawPtr() +
((nz_loc*j+k)*imap.num_elements()+i)*nsize_p[n]+ k*psize,1);
}
}
}
}
}
}
else
{
// construct velocity matrices and pressure systems at
// the same time resusing differential of velocity
// space
DNekScalMat &HelmMat = *(locExp->as<LocalRegions::Expansion>()
->GetLocMatrix(helmkey));
DNekScalMatSharedPtr MassMat;
Array<OneD, const NekDouble> HelmMat_data = HelmMat.GetOwnedMatrix()->GetPtr();
NekDouble HelmMatScale = HelmMat.Scale();
int HelmMatRows = HelmMat.GetRows();
if((lambda_imag != NekConstants::kNekUnsetDouble)&&(nz_loc == 2))
{
LocalRegions::MatrixKey masskey(StdRegions::eMass,
locExp->DetShapeType(),
*locExp);
MassMat = locExp->as<LocalRegions::Expansion>()
->GetLocMatrix(masskey);
}
Array<OneD, NekDouble> Advtmp;
Array<OneD, Array<OneD, NekDouble> > AdvDeriv(nvel*nvel);
// Use ExpList phys array for temporaary storage
Array<OneD, NekDouble> tmpphys = m_fields[0]->UpdatePhys();
int phys_offset = m_fields[m_velocity[0]]->GetPhys_Offset(eid);
int nv;
int npoints = locExp->GetTotPoints();
// Calculate derivative of base flow
if(IsLinearNSEquation)
{
int nv1;
int cnt = 0;
AdvDeriv[0] = Array<OneD, NekDouble>(nvel*nvel*npoints);
for(nv = 0; nv < nvel; ++nv)
{
for(nv1 = 0; nv1 < nvel; ++nv1)
{
if(cnt < nvel*nvel-1)
{
AdvDeriv[cnt+1] = AdvDeriv[cnt] + npoints;
++cnt;
}
if((nv1 == 2)&&(m_HomogeneousType == eHomogeneous1D))
{
Vmath::Zero(npoints,AdvDeriv[nv*nvel+nv1],1); // dU/dz = 0
}
else
{
locExp->PhysDeriv(MultiRegions::DirCartesianMap[nv1],Advfield[nv] + phys_offset, AdvDeriv[nv*nvel+nv1]);
}
}
}
}
for(i = 0; i < nbmap; ++i)
{
// Fill element with mode
Vmath::Zero(ncoeffs,coeffs,1);
coeffs[bmap[i]] = 1.0;
locExp->BwdTrans(coeffs,phys);
for(k = 0; k < nvel*nz_loc; ++k)
{
for(j = 0; j < nbmap; ++j)
{
// Ah_data[i+k*nbmap + (j+k*nbmap)*AhRows] += m_kinvis*HelmMat(bmap[i],bmap[j]);
Ah_data[i+k*nbmap + (j+k*nbmap)*AhRows] += m_kinvis*HelmMatScale*HelmMat_data[bmap[i] + HelmMatRows*bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
B_data[i+k*nbmap + (j+k*nimap)*nbndry] += m_kinvis*HelmMatScale*HelmMat_data[bmap[i]+HelmMatRows*imap[j]];
}
}
if((lambda_imag != NekConstants::kNekUnsetDouble)&&(nz_loc == 2))
{
for(k = 0; k < nvel; ++k)
{
for(j = 0; j < nbmap; ++j)
{
Ah_data[i+2*k*nbmap + (j+(2*k+1)*nbmap)*AhRows] -= lambda_imag*(*MassMat)(bmap[i],bmap[j]);
}
for(j = 0; j < nbmap; ++j)
{
Ah_data[i+(2*k+1)*nbmap + (j+2*k*nbmap)*AhRows] += lambda_imag*(*MassMat)(bmap[i],bmap[j]);
}
for(j = 0; j < nimap; ++j)
{
B_data[i+2*k*nbmap + (j+(2*k+1)*nimap)*nbndry] -= lambda_imag*(*MassMat)(bmap[i],imap[j]);
}
for(j = 0; j < nimap; ++j)
{
B_data[i+(2*k+1)*nbmap + (j+2*k*nimap)*nbndry] += lambda_imag*(*MassMat)(bmap[i],imap[j]);
}
}
}
for(k = 0; k < nvel; ++k)
{
if((nz_loc == 2)&&(k == 2)) // handle d/dz derivative
{
NekDouble beta = -2*M_PI*HomogeneousMode/m_LhomZ;
// Real Component
Vmath::Smul(npoints,beta,phys,1,deriv,1);
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dbnd->GetRawPtr() +
((nz_loc*k+1)*bmap.num_elements()+i)*nsize_p[n],1);
// Imaginary Component
Vmath::Neg(psize,pcoeffs,1);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dbnd->GetRawPtr() +
((nz_loc*k)*bmap.num_elements()+i)*nsize_p[n]+psize,1);
// now do advection terms
Vmath::Vmul(npoints,
Advtmp = Advfield[k] + phys_offset,
1,deriv,1,tmpphys,1);
locExp->IProductWRTBase(tmpphys,coeffs);
// real contribution
for(nv = 0; nv < nvel; ++nv)
{
for(j = 0; j < nbmap; ++j)
{
Ah_data[j+2*nv*nbmap + (i+(2*nv+1)*nbmap)*AhRows] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
C_data[i+(2*nv+1)*nbmap + (j+2*nv*nimap)*nbndry] +=
coeffs[imap[j]];
}
}
Vmath::Neg(ncoeffs,coeffs,1);
// imaginary contribution
for(nv = 0; nv < nvel; ++nv)
{
for(j = 0; j < nbmap; ++j)
{
Ah_data[j+(2*nv+1)*nbmap + (i+2*nv*nbmap)*AhRows] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
C_data[i+2*nv*nbmap + (j+(2*nv+1)*nimap)*nbndry] +=
coeffs[imap[j]];
}
}
}
else
{
if(k < 2)
{
locExp->PhysDeriv(MultiRegions::DirCartesianMap[k],phys, deriv);
Vmath::Vmul(npoints,
Advtmp = Advfield[k] + phys_offset,
1,deriv,1,tmpphys,1);
locExp->IProductWRTBase(tmpphys,coeffs);
for(nv = 0; nv < nvel*nz_loc; ++nv)
{
for(j = 0; j < nbmap; ++j)
{
Ah_data[j+nv*nbmap + (i+nv*nbmap)*AhRows] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
C_data[i+nv*nbmap + (j+nv*nimap)*nbndry] +=
coeffs[imap[j]];
}
}
// copy into column major storage.
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
for(j = 0; j < nz_loc; ++j)
{
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dbnd->GetRawPtr() +
((nz_loc*k+j)*bmap.num_elements() + i)*nsize_p[n]+ j*psize,1);
}
}
}
if(IsLinearNSEquation)
{
for(nv = 0; nv < nvel; ++nv)
{
// u' . Grad U terms
Vmath::Vmul(npoints,phys,1,
AdvDeriv[k*nvel+nv],
1,tmpphys,1);
locExp->IProductWRTBase(tmpphys,coeffs);
for(int n1 = 0; n1 < nz_loc; ++n1)
{
for(j = 0; j < nbmap; ++j)
{
Ah_data[j+(k*nz_loc+n1)*nbmap +
(i+(nv*nz_loc+n1)*nbmap)*AhRows] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
C_data[i+(nv*nz_loc+n1)*nbmap +
(j+(k*nz_loc+n1)*nimap)*nbndry] +=
coeffs[imap[j]];
}
}
}
}
}
}
for(i = 0; i < nimap; ++i)
{
// Fill element with mode
Vmath::Zero(ncoeffs,coeffs,1);
coeffs[imap[i]] = 1.0;
locExp->BwdTrans(coeffs,phys);
for(k = 0; k < nvel*nz_loc; ++k)
{
for(j = 0; j < nbmap; ++j) // C set up as transpose
{
C_data[j+k*nbmap + (i+k*nimap)*nbndry] += m_kinvis*HelmMatScale*HelmMat_data[imap[i]+HelmMatRows*bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
D_data[i+k*nimap + (j+k*nimap)*nint] += m_kinvis*HelmMatScale*HelmMat_data[imap[i]+HelmMatRows*imap[j]];
}
}
if((lambda_imag != NekConstants::kNekUnsetDouble)&&(nz_loc == 2))
{
for(k = 0; k < nvel; ++k)
{
for(j = 0; j < nbmap; ++j) // C set up as transpose
{
C_data[j+2*k*nbmap + (i+(2*k+1)*nimap)*nbndry] += lambda_imag*(*MassMat)(bmap[j],imap[i]);
}
for(j = 0; j < nbmap; ++j) // C set up as transpose
{
C_data[j+(2*k+1)*nbmap + (i+2*k*nimap)*nbndry] -= lambda_imag*(*MassMat)(bmap[j],imap[i]);
}
for(j = 0; j < nimap; ++j)
{
D_data[i+2*k*nimap + (j+(2*k+1)*nimap)*nint] -= lambda_imag*(*MassMat)(imap[i],imap[j]);
}
for(j = 0; j < nimap; ++j)
{
D_data[i+(2*k+1)*nimap + (j+2*k*nimap)*nint] += lambda_imag*(*MassMat)(imap[i],imap[j]);
}
}
}
for(k = 0; k < nvel; ++k)
{
if((nz_loc == 2)&&(k == 2)) // handle d/dz derivative
{
NekDouble beta = -2*M_PI*HomogeneousMode/m_LhomZ;
// Real Component
Vmath::Smul(npoints,beta,phys,1,deriv,1);
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dint->GetRawPtr() +
((nz_loc*k+1)*imap.num_elements()+i)*nsize_p[n],1);
// Imaginary Component
Vmath::Neg(psize,pcoeffs,1);
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dint->GetRawPtr() +
((nz_loc*k)*imap.num_elements()+i)*nsize_p[n]+psize,1);
// Advfield[k] *d/dx_k to all velocity
// components on diagonal
Vmath::Vmul(npoints, Advtmp = Advfield[k] + phys_offset,1,deriv,1,tmpphys,1);
locExp->IProductWRTBase(tmpphys,coeffs);
// Real Components
for(nv = 0; nv < nvel; ++nv)
{
for(j = 0; j < nbmap; ++j)
{
B_data[j+2*nv*nbmap + (i+(2*nv+1)*nimap)*nbndry] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
D_data[j+2*nv*nimap + (i+(2*nv+1)*nimap)*nint] +=
coeffs[imap[j]];
}
}
Vmath::Neg(ncoeffs,coeffs,1);
// Imaginary
for(nv = 0; nv < nvel; ++nv)
{
for(j = 0; j < nbmap; ++j)
{
B_data[j+(2*nv+1)*nbmap + (i+2*nv*nimap)*nbndry] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
D_data[j+(2*nv+1)*nimap + (i+2*nv*nimap)*nint] +=
coeffs[imap[j]];
}
}
}
else
{
if(k < 2)
{
// Differentiation & Inner product wrt base.
//locExp->PhysDeriv(k,phys, deriv);
locExp->PhysDeriv(MultiRegions::DirCartesianMap[k],phys,deriv);
Vmath::Vmul(npoints,
Advtmp = Advfield[k] + phys_offset,
1,deriv,1,tmpphys,1);
locExp->IProductWRTBase(tmpphys,coeffs);
for(nv = 0; nv < nvel*nz_loc; ++nv)
{
for(j = 0; j < nbmap; ++j)
{
B_data[j+nv*nbmap + (i+nv*nimap)*nbndry] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
D_data[j+nv*nimap + (i+nv*nimap)*nint] +=
coeffs[imap[j]];
}
}
// copy into column major storage.
m_pressure->GetExp(eid)->IProductWRTBase(deriv,pcoeffs);
for(j = 0; j < nz_loc; ++j)
{
Blas::Dcopy(psize,&(pcoeffs)[0],1,
Dint->GetRawPtr() +
((nz_loc*k+j)*imap.num_elements() + i)*nsize_p[n]+j*psize,1);
}
}
}
if(IsLinearNSEquation)
{
int n1;
for(nv = 0; nv < nvel; ++nv)
{
// u'.Grad U terms
Vmath::Vmul(npoints,phys,1,
AdvDeriv[k*nvel+nv],
1,tmpphys,1);
locExp->IProductWRTBase(tmpphys,coeffs);
for(n1 = 0; n1 < nz_loc; ++n1)
{
for(j = 0; j < nbmap; ++j)
{
B_data[j+(k*nz_loc+n1)*nbmap +
(i+(nv*nz_loc+n1)*nimap)*nbndry] +=
coeffs[bmap[j]];
}
for(j = 0; j < nimap; ++j)
{
D_data[j+(k*nz_loc+n1)*nimap +
(i+(nv*nz_loc+n1)*nimap)*nint] +=
coeffs[imap[j]];
}
}
}
}
}
}
D->Invert();
(*B) = (*B)*(*D);
// perform (*Ah) = (*Ah) - (*B)*(*C) but since size of
// Ah is larger than (*B)*(*C) easier to call blas
// directly
Blas::Dgemm('N','T', B->GetRows(), C->GetRows(),
B->GetColumns(), -1.0, B->GetRawPtr(),
B->GetRows(), C->GetRawPtr(),
C->GetRows(), 1.0,
Ah->GetRawPtr(), Ah->GetRows());
}
mat.m_BCinv->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,B));
mat.m_Btilde->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,C));
mat.m_Cinv->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,D));
mat.m_D_bnd->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one, Dbnd));
mat.m_D_int->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one, Dint));
// Do matrix manipulations and get final set of block matries
// reset boundary to put mean mode into boundary system.
DNekMatSharedPtr Cinv,BCinv,Btilde;
DNekMat DintCinvDTint, BCinvDTint_m_DTbnd, DintCinvBTtilde_m_Dbnd;
Cinv = D;
BCinv = B;
Btilde = C;
DintCinvDTint = (*Dint)*(*Cinv)*Transpose(*Dint);
BCinvDTint_m_DTbnd = (*BCinv)*Transpose(*Dint) - Transpose(*Dbnd);
// This could be transpose of BCinvDint in some cases
DintCinvBTtilde_m_Dbnd = (*Dint)*(*Cinv)*Transpose(*Btilde) - (*Dbnd);
// Set up final set of matrices.
DNekMatSharedPtr Bh = MemoryManager<DNekMat>::AllocateSharedPtr(nsize_bndry_p1[n],nsize_p_m1[n],zero);
DNekMatSharedPtr Ch = MemoryManager<DNekMat>::AllocateSharedPtr(nsize_p_m1[n],nsize_bndry_p1[n],zero);
DNekMatSharedPtr Dh = MemoryManager<DNekMat>::AllocateSharedPtr(nsize_p_m1[n], nsize_p_m1[n],zero);
Array<OneD, NekDouble> Dh_data = Dh->GetPtr();
// Copy matrices into final structures.
int n1,n2;
for(n1 = 0; n1 < nz_loc; ++n1)
{
for(i = 0; i < psize-1; ++i)
{
for(n2 = 0; n2 < nz_loc; ++n2)
{
for(j = 0; j < psize-1; ++j)
{
//(*Dh)(i+n1*(psize-1),j+n2*(psize-1)) =
//-DintCinvDTint(i+1+n1*psize,j+1+n2*psize);
Dh_data[(i+n1*(psize-1)) + (j+n2*(psize-1))*Dh->GetRows()] =
-DintCinvDTint(i+1+n1*psize,j+1+n2*psize);
}
}
}
}
for(n1 = 0; n1 < nz_loc; ++n1)
{
for(i = 0; i < nsize_bndry_p1[n]-nz_loc; ++i)
{
(*Ah)(i,nsize_bndry_p1[n]-nz_loc+n1) = BCinvDTint_m_DTbnd(i,n1*psize);
(*Ah)(nsize_bndry_p1[n]-nz_loc+n1,i) = DintCinvBTtilde_m_Dbnd(n1*psize,i);
}
}
for(n1 = 0; n1 < nz_loc; ++n1)
{
for(n2 = 0; n2 < nz_loc; ++n2)
{
(*Ah)(nsize_bndry_p1[n]-nz_loc+n1,nsize_bndry_p1[n]-nz_loc+n2) =
-DintCinvDTint(n1*psize,n2*psize);
}
}
for(n1 = 0; n1 < nz_loc; ++n1)
{
for(j = 0; j < psize-1; ++j)
{
for(i = 0; i < nsize_bndry_p1[n]-nz_loc; ++i)
{
(*Bh)(i,j+n1*(psize-1)) = BCinvDTint_m_DTbnd(i,j+1+n1*psize);
(*Ch)(j+n1*(psize-1),i) = DintCinvBTtilde_m_Dbnd(j+1+n1*psize,i);
}
}
}
for(n1 = 0; n1 < nz_loc; ++n1)
{
for(n2 = 0; n2 < nz_loc; ++n2)
{
for(j = 0; j < psize-1; ++j)
{
(*Bh)(nsize_bndry_p1[n]-nz_loc+n1,j+n2*(psize-1)) = -DintCinvDTint(n1*psize,j+1+n2*psize);
(*Ch)(j+n2*(psize-1),nsize_bndry_p1[n]-nz_loc+n1) = -DintCinvDTint(j+1+n2*psize,n1*psize);
}
}
}
// Do static condensation
Dh->Invert();
(*Bh) = (*Bh)*(*Dh);
//(*Ah) = (*Ah) - (*Bh)*(*Ch);
Blas::Dgemm('N','N', Bh->GetRows(), Ch->GetColumns(), Bh->GetColumns(), -1.0,
Bh->GetRawPtr(), Bh->GetRows(), Ch->GetRawPtr(), Ch->GetRows(),
1.0, Ah->GetRawPtr(), Ah->GetRows());
// Set matrices for later inversion. Probably do not need to be
// attached to class
pAh->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,Ah));
pBh->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,Bh));
pCh->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,Ch));
pDh->SetBlock(n,n,loc_mat = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,Dh));
}
timer.Stop();
cout << "Matrix Setup Costs: " << timer.TimePerTest(1) << endl;
timer.Start();
// Set up global coupled boundary solver.
// This is a key to define the solution matrix type
// currently we are giving it a argument of eLInearAdvectionReaction
// since this then makes the matrix storage of type eFull
MultiRegions::GlobalLinSysKey key(StdRegions::eLinearAdvectionReaction,locToGloMap);
mat.m_CoupledBndSys = MemoryManager<MultiRegions::GlobalLinSysDirectStaticCond>::AllocateSharedPtr(key,m_fields[0],pAh,pBh,pCh,pDh,locToGloMap);
mat.m_CoupledBndSys->Initialise(locToGloMap);
timer.Stop();
cout << "Multilevel condensation: " << timer.TimePerTest(1) << endl;
}
void Nektar::CoupledLinearNS::Solve ( void  )

Definition at line 1495 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::eHomogeneous1D, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::IncNavierStokes::m_forcing, Nektar::SolverUtils::EquationSystem::m_HomogeneousType, m_singleMode, Nektar::IncNavierStokes::m_velocity, and SolveLinearNS().

Referenced by v_DoInitialise(), and v_DoSolve().

{
const unsigned int ncmpt = m_velocity.num_elements();
Array<OneD, Array<OneD, NekDouble> > forcing_phys(ncmpt);
Array<OneD, Array<OneD, NekDouble> > forcing (ncmpt);
for(int i = 0; i < ncmpt; ++i)
{
forcing_phys[i] = Array<OneD, NekDouble> (m_fields[m_velocity[0]]->GetNpoints(), 0.0);
forcing[i] = Array<OneD, NekDouble> (m_fields[m_velocity[0]]->GetNcoeffs(),0.0);
}
std::vector<SolverUtils::ForcingSharedPtr>::const_iterator x;
for (x = m_forcing.begin(); x != m_forcing.end(); ++x)
{
const NekDouble time = 0;
(*x)->Apply(m_fields, forcing_phys, forcing_phys, time);
}
for (unsigned int i = 0; i < ncmpt; ++i)
{
m_fields[i]->IProductWRTBase(forcing_phys[i], forcing[i]);
if(m_HomogeneousType == eHomogeneous1D)
{
if(!m_singleMode) // Do not want to Fourier transoform in case of single mode stability an
{
m_fields[i]->HomogeneousFwdTrans(forcing[i], forcing[i]);
}
}
}
SolveLinearNS(forcing);
}
void Nektar::CoupledLinearNS::SolveLinearNS ( const Array< OneD, Array< OneD, NekDouble > > &  forcing)

Solve the coupled linear Navier-Stokes solve using matrix systems set up at construction. The solution is stored in m_velocity and m_pressure.

Parameters
forcingA list of forcing functions for each velocity component

The routine involves two levels of static condensations. Initially we require a statically condensed forcing function which requires the following manipulation

\[ {F\_bnd} = {\bf f}_{bnd} -m\_B \,m\_Cinv\, {\bf f}_{int}, \hspace{1cm} F\_p = m\_D\_{int}\, m\_Cinv\, {\bf f}_{int} \]

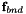Where ${\bf f}_{bnd}$ denote the forcing degrees of freedom of the elemental velocities on the boundary of the element, 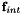${\bf f}_{int}$ denote the forcing degrees of freedom of the elemental velocities on the interior of the element. (see detailed description for more details).

This vector is further manipulated into

\[ Fh\_{bnd} = \left [ \begin{array}{c} f\_{bnd} -m\_B \, m\_Cinv\, {\bf f}_{int}\\ \left [m\_D\_{int} \, m\_Cinv \,{\bf f}_{int} \right]_0 \end{array}\right ] \hspace{1cm} [Fh\_p]_{i} = \begin{array}{c} [m\_D\_{int} \, m\_Cinv \, {\bf f}_{int}]_{i+1} \end{array} \]

where $-{[}m\_D\_{int}^T\, m\_Cinv \,{\bf f}_{int}]_0$ which is corresponds to the mean mode of the pressure degrees of freedom and is now added to the boundary system and the remainder of the block becomes the interior forcing for the inner static condensation (see detailed description for more details) which is set up in a GlobalLinSysDirectStaticCond class.

Finally we perform the final maniplation of the forcing to using hte

\[ Fh\_{bnd} = Fh\_{bnd} - m\_Bh \,m\_Chinv \, Fh\_p \]

We can now call the solver to the global coupled boundary system (through the call to #m_CoupledBndSys->Solve) to obtain the velocity boundary solution as the mean pressure solution, i.e.

\[ {\cal A}^T(\hat{A} - \hat{C}^T \hat{D}^{-1} \hat{B} ){\cal A} \, Bnd = Fh\_{bnd} \]

Once we know the solution to the above the rest of the pressure modes are recoverable thorugh

\[ Ph = m\_Dhinv\, (Bnd - m\_Ch^T \, Fh_{bnd}) \]

We can now unpack 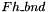$ Fh\_{bnd} $ (last elemental mode) and 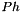$ Ph $ into m_pressure and 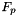$ F_p$ and $ F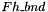h\_{bnd}$ into a closed pack list of boundary velocoity degrees of freedom stored in $ F\_bnd$.

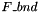Finally the interior velocity degrees of freedom are then obtained through the relationship

\[ F\_{int} = m\_Cinv\ ( F\_{int} + m\_D\_{int}^T\, F\_p - m\_Btilde^T\, Bnd) \]

We then unpack the solution back to the MultiRegion structures m_velocity and m_pressure

Definition at line 1869 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::eHomogeneous1D, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_HomogeneousType, Nektar::SolverUtils::EquationSystem::m_npointsZ, Nektar::IncNavierStokes::m_pressure, and Nektar::IncNavierStokes::m_velocity.

Referenced by Continuation(), Solve(), SolveSteadyNavierStokes(), and SolveUnsteadyStokesSystem().

{
int i,n;
Array<OneD, MultiRegions::ExpListSharedPtr> vel_fields(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > force(m_velocity.num_elements());
if(m_HomogeneousType == eHomogeneous1D)
{
int ncoeffsplane = m_fields[m_velocity[0]]->GetPlane(0)->GetNcoeffs();
for(n = 0; n < m_npointsZ/2; ++n)
{
// Get the a Fourier mode of velocity and forcing components.
for(i = 0; i < m_velocity.num_elements(); ++i)
{
vel_fields[i] = m_fields[m_velocity[i]]->GetPlane(2*n);
// Note this needs to correlate with how we pass forcing
force[i] = forcing[i] + 2*n*ncoeffsplane;
}
SolveLinearNS(force,vel_fields,m_pressure->GetPlane(2*n),n);
}
for(i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->SetPhysState(false);
}
m_pressure->SetPhysState(false);
}
else
{
for(i = 0; i < m_velocity.num_elements(); ++i)
{
vel_fields[i] = m_fields[m_velocity[i]];
// Note this needs to correlate with how we pass forcing
force[i] = forcing[i];
}
SolveLinearNS(force,vel_fields,m_pressure);
}
}
void Nektar::CoupledLinearNS::SolveLinearNS ( const Array< OneD, Array< OneD, NekDouble > > &  forcing,
Array< OneD, MultiRegions::ExpListSharedPtr > &  fields,
MultiRegions::ExpListSharedPtr &  pressure,
const int  HomogeneousMode = 0 
)

Definition at line 1908 of file CoupledLinearNS.cpp.

References Nektar::SpatialDomains::eDirichlet, Nektar::SolverUtils::EquationSystem::eHomogeneous1D, Nektar::eSteadyNavierStokes, Nektar::eWrapper, Nektar::SolverUtils::EquationSystem::GetNcoeffs(), Nektar::IncNavierStokes::m_equationType, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_HomogeneousType, m_initialStep, m_locToGloMap, m_mat, m_singleMode, Nektar::IncNavierStokes::m_velocity, Nektar::Transpose(), and Vmath::Zero().

{
int i,j,k,n,eid,cnt,cnt1;
int nbnd,nint,offset;
int nvel = m_velocity.num_elements();
int nel = fields[0]->GetNumElmts();
Array<OneD, unsigned int> bmap, imap;
Array<OneD, NekDouble > f_bnd(m_mat[mode].m_BCinv->GetRows());
NekVector< NekDouble > F_bnd(f_bnd.num_elements(), f_bnd, eWrapper);
Array<OneD, NekDouble > f_int(m_mat[mode].m_BCinv->GetColumns());
NekVector< NekDouble > F_int(f_int.num_elements(),f_int, eWrapper);
int nz_loc;
int nplanecoeffs = fields[m_velocity[0]]->GetNcoeffs();// this is fine since we pass the nplane coeff data.
if(mode) // Homogeneous mode flag
{
nz_loc = 2;
}
else
{
if(m_singleMode)
{
nz_loc = 2;
}
else
{
nz_loc = 1;
if(m_HomogeneousType == eHomogeneous1D)
{
// Zero fields to set complex mode to zero;
for(i = 0; i < fields.num_elements(); ++i)
{
Vmath::Zero(2*fields[i]->GetNcoeffs(),fields[i]->UpdateCoeffs(),1);
}
Vmath::Zero(2*pressure->GetNcoeffs(),pressure->UpdateCoeffs(),1);
}
}
}
// Assemble f_bnd and f_int
cnt = cnt1 = 0;
for(i = 0; i < nel; ++i) // loop over elements
{
eid = fields[m_velocity[0]]->GetOffset_Elmt_Id(i);
fields[m_velocity[0]]->GetExp(eid)->GetBoundaryMap(bmap);
fields[m_velocity[0]]->GetExp(eid)->GetInteriorMap(imap);
nbnd = bmap.num_elements();
nint = imap.num_elements();
offset = fields[m_velocity[0]]->GetCoeff_Offset(eid);
for(j = 0; j < nvel; ++j) // loop over velocity fields
{
for(n = 0; n < nz_loc; ++n)
{
for(k = 0; k < nbnd; ++k)
{
f_bnd[cnt+k] = forcing[j][n*nplanecoeffs +
offset+bmap[k]];
}
for(k = 0; k < nint; ++k)
{
f_int[cnt1+k] = forcing[j][n*nplanecoeffs +
offset+imap[k]];
}
cnt += nbnd;
cnt1 += nint;
}
}
}
Array<OneD, NekDouble > f_p(m_mat[mode].m_D_int->GetRows());
NekVector< NekDouble > F_p(f_p.num_elements(),f_p,eWrapper);
NekVector< NekDouble > F_p_tmp(m_mat[mode].m_Cinv->GetRows());
// fbnd does not currently hold the pressure mean
F_bnd = F_bnd - (*m_mat[mode].m_BCinv)*F_int;
F_p_tmp = (*m_mat[mode].m_Cinv)*F_int;
F_p = (*m_mat[mode].m_D_int) * F_p_tmp;
// construct inner forcing
Array<OneD, NekDouble > bnd (m_locToGloMap[mode]->GetNumGlobalCoeffs(),0.0);
Array<OneD, NekDouble > fh_bnd(m_locToGloMap[mode]->GetNumGlobalCoeffs(),0.0);
const Array<OneD,const int>& loctoglomap
= m_locToGloMap[mode]->GetLocalToGlobalMap();
const Array<OneD,const NekDouble>& loctoglosign
= m_locToGloMap[mode]->GetLocalToGlobalSign();
offset = cnt = 0;
for(i = 0; i < nel; ++i)
{
eid = fields[0]->GetOffset_Elmt_Id(i);
nbnd = nz_loc*fields[0]->GetExp(eid)->NumBndryCoeffs();
for(j = 0; j < nvel; ++j)
{
for(k = 0; k < nbnd; ++k)
{
fh_bnd[loctoglomap[offset+j*nbnd+k]] +=
loctoglosign[offset+j*nbnd+k]*f_bnd[cnt+k];
}
cnt += nbnd;
}
nint = pressure->GetExp(eid)->GetNcoeffs();
offset += nvel*nbnd + nint*nz_loc;
}
offset = cnt1 = 0;
for(i = 0; i < nel; ++i)
{
eid = fields[0]->GetOffset_Elmt_Id(i);
nbnd = nz_loc*fields[0]->GetExp(eid)->NumBndryCoeffs();
nint = pressure->GetExp(eid)->GetNcoeffs();
for(n = 0; n < nz_loc; ++n)
{
for(j = 0; j < nint; ++j)
{
fh_bnd[loctoglomap[offset + nvel*nbnd + n*nint+j]] = f_p[cnt1+j];
}
cnt1 += nint;
}
offset += nvel*nbnd + nz_loc*nint;
}
// Set Weak BC into f_bnd and Dirichlet Dofs in bnd
const Array<OneD,const int>& bndmap
= m_locToGloMap[mode]->GetBndCondCoeffsToGlobalCoeffsMap();
// Forcing function with weak boundary conditions and
// Dirichlet conditions
int bndcnt=0;
for(k = 0; k < nvel; ++k)
{
const Array<OneD, SpatialDomains::BoundaryConditionShPtr> bndConds = fields[k]->GetBndConditions();
Array<OneD, const MultiRegions::ExpListSharedPtr> bndCondExp;
if(m_HomogeneousType == eHomogeneous1D)
{
bndCondExp = m_fields[k]->GetPlane(2*mode)->GetBndCondExpansions();
}
else
{
bndCondExp = m_fields[k]->GetBndCondExpansions();
}
for(i = 0; i < bndCondExp.num_elements(); ++i)
{
const Array<OneD, const NekDouble > bndCondCoeffs = bndCondExp[i]->GetCoeffs();
cnt = 0;
for(n = 0; n < nz_loc; ++n)
{
if(bndConds[i]->GetBoundaryConditionType()
== SpatialDomains::eDirichlet)
{
for(j = 0; j < (bndCondExp[i])->GetNcoeffs(); j++)
{
if (m_equationType == eSteadyNavierStokes && m_initialStep == false)
{
//This condition set all the Dirichlet BC at 0 after
//the initial step of the Newton method
bnd[bndmap[bndcnt++]] = 0;
}
else
{
bnd[bndmap[bndcnt++]] = bndCondCoeffs[cnt++];
}
}
}
else
{
for(j = 0; j < (bndCondExp[i])->GetNcoeffs(); j++)
{
fh_bnd[bndmap[bndcnt++]]
+= bndCondCoeffs[cnt++];
}
}
}
}
}
m_mat[mode].m_CoupledBndSys->Solve(fh_bnd,bnd,m_locToGloMap[mode]);
// unpack pressure and velocity boundary systems.
offset = cnt = 0;
int totpcoeffs = pressure->GetNcoeffs();
Array<OneD, NekDouble> p_coeffs = pressure->UpdateCoeffs();
for(i = 0; i < nel; ++i)
{
eid = fields[0]->GetOffset_Elmt_Id(i);
nbnd = nz_loc*fields[0]->GetExp(eid)->NumBndryCoeffs();
nint = pressure->GetExp(eid)->GetNcoeffs();
for(j = 0; j < nvel; ++j)
{
for(k = 0; k < nbnd; ++k)
{
f_bnd[cnt+k] = loctoglosign[offset+j*nbnd+k]*bnd[loctoglomap[offset + j*nbnd + k]];
}
cnt += nbnd;
}
offset += nvel*nbnd + nint*nz_loc;
}
pressure->SetPhysState(false);
offset = cnt = cnt1 = 0;
for(i = 0; i < nel; ++i)
{
eid = fields[0]->GetOffset_Elmt_Id(i);
nint = pressure->GetExp(eid)->GetNcoeffs();
nbnd = fields[0]->GetExp(eid)->NumBndryCoeffs();
cnt1 = pressure->GetCoeff_Offset(eid);
for(n = 0; n < nz_loc; ++n)
{
for(j = 0; j < nint; ++j)
{
p_coeffs[n*totpcoeffs + cnt1+j] =
f_p[cnt+j] = bnd[loctoglomap[offset +
(nvel*nz_loc)*nbnd +
n*nint + j]];
}
cnt += nint;
}
offset += (nvel*nbnd + nint)*nz_loc;
}
// Back solve first level of static condensation for interior
// velocity space and store in F_int
F_int = F_int + Transpose(*m_mat[mode].m_D_int)*F_p
- Transpose(*m_mat[mode].m_Btilde)*F_bnd;
F_int = (*m_mat[mode].m_Cinv)*F_int;
// Unpack solution from Bnd and F_int to v_coeffs
cnt = cnt1 = 0;
for(i = 0; i < nel; ++i) // loop over elements
{
eid = fields[m_velocity[0]]->GetOffset_Elmt_Id(i);
fields[0]->GetExp(eid)->GetBoundaryMap(bmap);
fields[0]->GetExp(eid)->GetInteriorMap(imap);
nbnd = bmap.num_elements();
nint = imap.num_elements();
offset = fields[0]->GetCoeff_Offset(eid);
for(j = 0; j < nvel; ++j) // loop over velocity fields
{
for(n = 0; n < nz_loc; ++n)
{
for(k = 0; k < nbnd; ++k)
{
fields[j]->SetCoeff(n*nplanecoeffs +
offset+bmap[k],
f_bnd[cnt+k]);
}
for(k = 0; k < nint; ++k)
{
fields[j]->SetCoeff(n*nplanecoeffs +
offset+imap[k],
f_int[cnt1+k]);
}
cnt += nbnd;
cnt1 += nint;
}
}
}
for(j = 0; j < nvel; ++j)
{
fields[j]->SetPhysState(false);
}
}
void Nektar::CoupledLinearNS::SolveSteadyNavierStokes ( void  )

Definition at line 1558 of file CoupledLinearNS.cpp.

References ASSERTL0, EvaluateNewtonRHS(), L2Norm(), m_counter, Nektar::SolverUtils::EquationSystem::m_fields, m_initialStep, Nektar::IncNavierStokes::m_kinvis, m_MatrixSetUpStep, m_tol, Nektar::IncNavierStokes::m_velocity, SetUpCoupledMatrix(), SolveLinearNS(), Nektar::Timer::Start(), Nektar::Timer::Stop(), Nektar::Timer::TimePerTest(), and Vmath::Vadd().

Referenced by v_DoSolve().

{
Timer Newtontimer;
Newtontimer.Start();
Array<OneD, Array<OneD, NekDouble> > RHS_Coeffs(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > RHS_Phys(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> > delta_velocity_Phys(m_velocity.num_elements());
Array<OneD, Array<OneD, NekDouble> >Velocity_Phys(m_velocity.num_elements());
Array<OneD, NekDouble > L2_norm(m_velocity.num_elements(), 1.0);
Array<OneD, NekDouble > Inf_norm(m_velocity.num_elements(), 1.0);
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
delta_velocity_Phys[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),1.0);
Velocity_Phys[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
}
m_counter=1;
L2Norm(delta_velocity_Phys, L2_norm);
//while(max(Inf_norm[0], Inf_norm[1]) > m_tol)
while(max(L2_norm[0], L2_norm[1]) > m_tol)
{
if(m_counter == 1) //At the first Newton step, we use the solution of the Stokes problem (if Restart=0 in input file)
//Or the solution of the .rst file (if Restart=1 in input file)
{
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
RHS_Coeffs[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetNcoeffs(),0.0);
RHS_Phys[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
}
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->BwdTrans_IterPerExp(m_fields[m_velocity[i]]->GetCoeffs(), Velocity_Phys[i]);
}
m_initialStep = true;
EvaluateNewtonRHS(Velocity_Phys, RHS_Coeffs);
SetUpCoupledMatrix(0.0, Velocity_Phys, true);
SolveLinearNS(RHS_Coeffs);
m_initialStep = false;
}
if(m_counter > 1)
{
EvaluateNewtonRHS(Velocity_Phys, RHS_Coeffs);
if(m_counter%m_MatrixSetUpStep == 0) //Setting Up the matrix is expensive. We do it at each "m_MatrixSetUpStep" step.
{
SetUpCoupledMatrix(0.0, Velocity_Phys, true);
}
SolveLinearNS(RHS_Coeffs);
}
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->BwdTrans_IterPerExp(RHS_Coeffs[i], RHS_Phys[i]);
m_fields[m_velocity[i]]->BwdTrans_IterPerExp(m_fields[m_velocity[i]]->GetCoeffs(), delta_velocity_Phys[i]);
}
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
Vmath::Vadd(Velocity_Phys[i].num_elements(),Velocity_Phys[i], 1, delta_velocity_Phys[i], 1,
Velocity_Phys[i], 1);
}
//InfNorm(delta_velocity_Phys, Inf_norm);
L2Norm(delta_velocity_Phys, L2_norm);
if(max(Inf_norm[0], Inf_norm[1]) > 100)
{
cout<<"\nThe Newton method has failed at m_kinvis = "<<m_kinvis<<" (<=> Re = " << 1/m_kinvis << ")"<< endl;
ASSERTL0(0, "The Newton method has failed... \n");
}
cout << "\n";
m_counter++;
}
if (m_counter > 1) //We save u:=u+\delta u in u->Coeffs
{
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->FwdTrans(Velocity_Phys[i], m_fields[m_velocity[i]]->UpdateCoeffs());
}
}
Newtontimer.Stop();
cout<<"We have done "<< m_counter-1 << " iteration(s) in " << Newtontimer.TimePerTest(1)/60 << " minute(s). \n\n";
}
void Nektar::CoupledLinearNS::SolveUnsteadyStokesSystem ( const Array< OneD, const Array< OneD, NekDouble > > &  inarray,
Array< OneD, Array< OneD, NekDouble > > &  outarray,
const NekDouble  time,
const NekDouble  a_iixDt 
)

Definition at line 1367 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::GetNcoeffs(), Nektar::SolverUtils::EquationSystem::m_fields, Nektar::IncNavierStokes::m_nConvectiveFields, Nektar::IncNavierStokes::m_velocity, Nektar::IncNavierStokes::SetBoundaryConditions(), SetUpCoupledMatrix(), Vmath::Smul(), and SolveLinearNS().

Referenced by v_DoInitialise().

{
int i;
Array<OneD, Array< OneD, NekDouble> > F(m_nConvectiveFields);
NekDouble lambda = 1.0/aii_Dt;
static NekDouble lambda_store;
Array <OneD, Array<OneD, NekDouble> > forcing(m_velocity.num_elements());
// Matrix solution
if(fabs(lambda_store - lambda) > 1e-10)
{
cout << "Setting up Stokes matrix problem [.";
fflush(stdout);
SetUpCoupledMatrix(lambda);
cout << "]" << endl;
lambda_store = lambda;
}
SetBoundaryConditions(time);
// Forcing for advection solve
for(i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->IProductWRTBase(inarray[i],m_fields[m_velocity[i]]->UpdateCoeffs());
Vmath::Smul(m_fields[m_velocity[i]]->GetNcoeffs(),lambda,m_fields[m_velocity[i]]->GetCoeffs(), 1,m_fields[m_velocity[i]]->UpdateCoeffs(),1);
forcing[i] = m_fields[m_velocity[i]]->GetCoeffs();
}
SolveLinearNS(forcing);
for(i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->BwdTrans(m_fields[m_velocity[i]]->GetCoeffs(),outarray[i]);
}
}
void Nektar::CoupledLinearNS::v_DoInitialise ( void  )
privatevirtual

Definition at line 1208 of file CoupledLinearNS.cpp.

References ASSERTL0, DefineForcingTerm(), Nektar::LibUtilities::TimeIntegrationSchemeOperators::DefineImplicitSolve(), Nektar::LibUtilities::TimeIntegrationSchemeOperators::DefineOdeRhs(), Nektar::eNoEquationType, Nektar::eSteadyLinearisedNS, Nektar::eSteadyNavierStokes, Nektar::eSteadyOseen, Nektar::eSteadyStokes, Nektar::eUnsteadyNavierStokes, Nektar::eUnsteadyStokes, EvaluateAdvection(), Nektar::SolverUtils::EquationSystem::EvaluateFunction(), Nektar::SolverUtils::EquationSystem::m_boundaryConditions, m_counter, Nektar::IncNavierStokes::m_equationType, Nektar::SolverUtils::EquationSystem::m_fields, m_initialStep, Nektar::IncNavierStokes::m_kinvis, m_kinvisMin, m_KinvisPercentage, Nektar::SolverUtils::EquationSystem::m_lambda, m_MatrixSetUpStep, m_maxIt, Nektar::SolverUtils::UnsteadySystem::m_ode, m_Restart, Nektar::SolverUtils::EquationSystem::m_session, m_tol, Nektar::IncNavierStokes::m_velocity, Nektar::SolverUtils::EquationSystem::SetInitialConditions(), SetUpCoupledMatrix(), Solve(), and SolveUnsteadyStokesSystem().

{
switch(m_equationType)
{
case eUnsteadyStokes:
case eUnsteadyNavierStokes:
{
// LibUtilities::TimeIntegrationMethod intMethod;
// std::string TimeIntStr = m_session->GetSolverInfo("TIMEINTEGRATIONMETHOD");
// int i;
// for(i = 0; i < (int) LibUtilities::SIZE_TimeIntegrationMethod; ++i)
// {
// if(boost::iequals(LibUtilities::TimeIntegrationMethodMap[i],TimeIntStr))
// {
// intMethod = (LibUtilities::TimeIntegrationMethod)i;
// break;
// }
// }
//
// ASSERTL0(i != (int) LibUtilities::SIZE_TimeIntegrationMethod, "Invalid time integration type.");
//
// m_integrationScheme = LibUtilities::GetTimeIntegrationWrapperFactory().CreateInstance(LibUtilities::TimeIntegrationMethodMap[intMethod]);
// Could defind this from IncNavierStokes class?
m_ode.DefineOdeRhs(&CoupledLinearNS::EvaluateAdvection, this);
m_ode.DefineImplicitSolve(&CoupledLinearNS::SolveUnsteadyStokesSystem,this);
// Set initial condition using time t=0
SetInitialConditions(0.0);
}
case eSteadyStokes:
SetUpCoupledMatrix(0.0);
break;
case eSteadyOseen:
{
Array<OneD, Array<OneD, NekDouble> > AdvField(m_velocity.num_elements());
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
AdvField[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
}
ASSERTL0(m_session->DefinesFunction("AdvectionVelocity"),
"Advection Velocity section must be defined in "
"session file.");
std::vector<std::string> fieldStr;
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
fieldStr.push_back(m_boundaryConditions->GetVariable(m_velocity[i]));
}
EvaluateFunction(fieldStr,AdvField,"AdvectionVelocity");
SetUpCoupledMatrix(0.0,AdvField,false);
}
break;
case eSteadyNavierStokes:
{
m_session->LoadParameter("KinvisMin", m_kinvisMin);
m_session->LoadParameter("KinvisPercentage", m_KinvisPercentage);
m_session->LoadParameter("Tolerence", m_tol);
m_session->LoadParameter("MaxIteration", m_maxIt);
m_session->LoadParameter("MatrixSetUpStep", m_MatrixSetUpStep);
m_session->LoadParameter("Restart", m_Restart);
DefineForcingTerm();
if (m_Restart == 1)
{
ASSERTL0(m_session->DefinesFunction("Restart"),
"Restart section must be defined in session file.");
Array<OneD, Array<OneD, NekDouble> > Restart(m_velocity.num_elements());
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
Restart[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
}
std::vector<std::string> fieldStr;
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
fieldStr.push_back(m_boundaryConditions->GetVariable(m_velocity[i]));
}
EvaluateFunction(fieldStr, Restart, "Restart");
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
m_fields[m_velocity[i]]->FwdTrans_IterPerExp(Restart[i], m_fields[m_velocity[i]]->UpdateCoeffs());
}
cout << "Saving the RESTART file for m_kinvis = "<< m_kinvis << " (<=> Re = " << 1/m_kinvis << ")" <<endl;
}
else //We solve the Stokes Problem
{
/*Array<OneD, Array<OneD, NekDouble> >ZERO(m_velocity.num_elements());
*
* for(int i = 0; i < m_velocity.num_elements(); ++i)
* {
* ZERO[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
* m_fields[m_velocity[i]]->FwdTrans(ZERO[i], m_fields[m_velocity[i]]->UpdateCoeffs());
}*/
SetUpCoupledMatrix(0.0);
m_initialStep = true;
m_counter=1;
//SolveLinearNS(m_ForcingTerm_Coeffs);
Solve();
m_initialStep = false;
cout << "Saving the Stokes Flow for m_kinvis = "<< m_kinvis << " (<=> Re = " << 1/m_kinvis << ")" <<endl;
}
}
break;
case eSteadyLinearisedNS:
{
SetInitialConditions(0.0);
Array<OneD, Array<OneD, NekDouble> > AdvField(m_velocity.num_elements());
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
AdvField[i] = Array<OneD, NekDouble> (m_fields[m_velocity[i]]->GetTotPoints(),0.0);
}
ASSERTL0(m_session->DefinesFunction("AdvectionVelocity"),
"Advection Velocity section must be defined in "
"session file.");
std::vector<std::string> fieldStr;
for(int i = 0; i < m_velocity.num_elements(); ++i)
{
fieldStr.push_back(m_boundaryConditions->GetVariable(m_velocity[i]));
}
EvaluateFunction(fieldStr,AdvField,"AdvectionVelocity");
SetUpCoupledMatrix(m_lambda,AdvField,true);
}
break;
case eNoEquationType:
default:
ASSERTL0(false,"Unknown or undefined equation type for CoupledLinearNS");
}
}
void Nektar::CoupledLinearNS::v_DoSolve ( void  )
privatevirtual

Definition at line 1430 of file CoupledLinearNS.cpp.

References ASSERTL0, Nektar::SolverUtils::EquationSystem::Checkpoint_Output(), Continuation(), Nektar::eNoEquationType, Nektar::eSteadyLinearisedNS, Nektar::eSteadyNavierStokes, Nektar::eSteadyOseen, Nektar::eSteadyStokes, Nektar::eUnsteadyNavierStokes, Nektar::eUnsteadyStokes, Nektar::IncNavierStokes::m_equationType, Nektar::IncNavierStokes::m_kinvis, m_kinvisMin, Solve(), SolveSteadyNavierStokes(), Nektar::Timer::Start(), Nektar::Timer::Stop(), and Nektar::Timer::TimePerTest().

{
switch(m_equationType)
{
case eUnsteadyStokes:
case eUnsteadyNavierStokes:
//AdvanceInTime(m_steps);
UnsteadySystem::v_DoSolve();
break;
case eSteadyStokes:
case eSteadyOseen:
case eSteadyLinearisedNS:
{
Solve();
break;
}
case eSteadyNavierStokes:
{
Timer Generaltimer;
Generaltimer.Start();
int Check(0);
//Saving the init datas
Checkpoint_Output(Check);
Check++;
cout<<"We execute INITIALLY SolveSteadyNavierStokes for m_kinvis = "<<m_kinvis<<" (<=> Re = "<<1/m_kinvis<<")"<<endl;
SolveSteadyNavierStokes();
while(m_kinvis > m_kinvisMin)
{
if (Check == 1)
{
cout<<"We execute SolveSteadyNavierStokes for m_kinvis = "<<m_kinvis<<" (<=> Re = "<<1/m_kinvis<<")"<<endl;
SolveSteadyNavierStokes();
Checkpoint_Output(Check);
Check++;
}
Continuation();
if (m_kinvis > m_kinvisMin)
{
cout<<"We execute SolveSteadyNavierStokes for m_kinvis = "<<m_kinvis<<" (<=> Re = "<<1/m_kinvis<<")"<<endl;
SolveSteadyNavierStokes();
Checkpoint_Output(Check);
Check++;
}
}
Generaltimer.Stop();
cout<<"\nThe total calculation time is : " << Generaltimer.TimePerTest(1)/60 << " minute(s). \n\n";
break;
}
case eNoEquationType:
default:
ASSERTL0(false,"Unknown or undefined equation type for CoupledLinearNS");
}
}
void Nektar::CoupledLinearNS::v_GenerateSummary ( SolverUtils::SummaryList &  s)
privatevirtual

Definition at line 1203 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::AddSummaryItem().

{
SolverUtils::AddSummaryItem(s, "Solver Type", "Coupled Linearised NS");
}
int Nektar::CoupledLinearNS::v_GetForceDimension ( void  )
privatevirtual

Definition at line 2223 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::m_session.

{
return m_session->GetVariables().size();
}
void Nektar::CoupledLinearNS::v_InitObject ( )
protectedvirtual

Init object for UnsteadySystem class.

Initialization object for UnsteadySystem class.

Reimplemented from Nektar::IncNavierStokes.

Definition at line 65 of file CoupledLinearNS.cpp.

References ASSERTL0, ASSERTL1, Nektar::LibUtilities::NekFactory< tKey, tBase, >::CreateInstance(), Nektar::SolverUtils::EquationSystem::eHomogeneous1D, Nektar::eUnsteadyNavierStokes, GenPressureExp(), Nektar::GetExtrapolateFactory(), Nektar::SolverUtils::AdvectionSystem::m_advObject, Nektar::SolverUtils::EquationSystem::m_boundaryConditions, Nektar::IncNavierStokes::m_equationType, Nektar::IncNavierStokes::m_extrapolation, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_graph, Nektar::SolverUtils::EquationSystem::m_homogen_dealiasing, Nektar::SolverUtils::EquationSystem::m_HomogeneousType, Nektar::SolverUtils::EquationSystem::m_LhomZ, m_locToGloMap, Nektar::IncNavierStokes::m_nConvectiveFields, Nektar::SolverUtils::EquationSystem::m_npointsZ, Nektar::IncNavierStokes::m_pressure, Nektar::SolverUtils::EquationSystem::m_session, m_singleMode, Nektar::SolverUtils::EquationSystem::m_useFFT, Nektar::IncNavierStokes::m_velocity, and m_zeroMode.

{
IncNavierStokes::v_InitObject();
int i;
int expdim = m_graph->GetMeshDimension();
// Get Expansion list for orthogonal expansion at p-2
const SpatialDomains::ExpansionMap &pressure_exp = GenPressureExp(m_graph->GetExpansions("u"));
m_nConvectiveFields = m_fields.num_elements();
if(boost::iequals(m_boundaryConditions->GetVariable(m_nConvectiveFields-1), "p"))
{
ASSERTL0(false,"Last field is defined as pressure but this is not suitable for this solver, please remove this field as it is implicitly defined");
}
// Decide how to declare explist for pressure.
if(expdim == 2)
{
int nz;
if(m_HomogeneousType == eHomogeneous1D)
{
ASSERTL0(m_fields.num_elements() > 2,"Expect to have three at least three components of velocity variables");
LibUtilities::BasisKey Homo1DKey = m_fields[0]->GetHomogeneousBasis()->GetBasisKey();
m_pressure = MemoryManager<MultiRegions::ExpList3DHomogeneous1D>::AllocateSharedPtr(m_session, Homo1DKey, m_LhomZ, m_useFFT,m_homogen_dealiasing, pressure_exp);
ASSERTL1(m_npointsZ%2==0,"Non binary number of planes have been specified");
nz = m_npointsZ/2;
}
else
{
//m_pressure2 = MemoryManager<MultiRegions::ContField2D>::AllocateSharedPtr(m_session, pressure_exp);
m_pressure = MemoryManager<MultiRegions::ExpList2D>::AllocateSharedPtr(m_session, pressure_exp);
nz = 1;
}
Array<OneD, MultiRegions::ExpListSharedPtr> velocity(m_velocity.num_elements());
for(i =0 ; i < m_velocity.num_elements(); ++i)
{
velocity[i] = m_fields[m_velocity[i]];
}
// Set up Array of mappings
m_locToGloMap = Array<OneD, CoupledLocalToGlobalC0ContMapSharedPtr> (nz);
if(m_session->DefinesSolverInfo("SingleMode"))
{
ASSERTL0(nz <=2 ,"For single mode calculation can only have nz <= 2");
m_singleMode = true;
if(m_session->DefinesSolverInfo("BetaZero"))
{
m_zeroMode = true;
}
int nz_loc = 2;
m_locToGloMap[0] = MemoryManager<CoupledLocalToGlobalC0ContMap>::AllocateSharedPtr(m_session,m_graph,m_boundaryConditions,velocity,m_pressure,nz_loc,m_zeroMode);
}
else
{
// base mode
int nz_loc = 1;
m_locToGloMap[0] = MemoryManager<CoupledLocalToGlobalC0ContMap>::AllocateSharedPtr(m_session,m_graph,m_boundaryConditions,velocity,m_pressure,nz_loc);
if(nz > 1)
{
nz_loc = 2;
// Assume all higher modes have the same boundary conditions and re-use mapping
m_locToGloMap[1] = MemoryManager<CoupledLocalToGlobalC0ContMap>::AllocateSharedPtr(m_session,m_graph,m_boundaryConditions,velocity,m_pressure->GetPlane(2),nz_loc,false);
// Note high order modes cannot be singular
for(i = 2; i < nz; ++i)
{
m_locToGloMap[i] = m_locToGloMap[1];
}
}
}
}
else if (expdim == 3)
{
//m_pressure = MemoryManager<MultiRegions::ExpList3D>::AllocateSharedPtr(pressure_exp);
ASSERTL0(false,"Setup mapping aray");
}
else
{
ASSERTL0(false,"Exp dimension not recognised");
}
// creation of the extrapolation object
if(m_equationType == eUnsteadyNavierStokes)
{
std::string vExtrapolation = "Standard";
if (m_session->DefinesSolverInfo("Extrapolation"))
{
vExtrapolation = m_session->GetSolverInfo("Extrapolation");
}
m_extrapolation = GetExtrapolateFactory().CreateInstance(
vExtrapolation,
m_session,
m_fields,
m_pressure,
m_velocity,
m_advObject);
}
}
void Nektar::CoupledLinearNS::v_Output ( void  )
privatevirtual

Definition at line 2185 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::GetNcoeffs(), Nektar::SolverUtils::EquationSystem::m_boundaryConditions, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::IncNavierStokes::m_pressure, Nektar::SolverUtils::EquationSystem::m_sessionName, m_singleMode, and Nektar::SolverUtils::EquationSystem::WriteFld().

{
std::vector<Array<OneD, NekDouble> > fieldcoeffs(m_fields.num_elements()+1);
std::vector<std::string> variables(m_fields.num_elements()+1);
int i;
for(i = 0; i < m_fields.num_elements(); ++i)
{
fieldcoeffs[i] = m_fields[i]->UpdateCoeffs();
variables[i] = m_boundaryConditions->GetVariable(i);
}
fieldcoeffs[i] = Array<OneD, NekDouble>(m_fields[0]->GetNcoeffs());
// project pressure field to velocity space
if(m_singleMode==true)
{
Array<OneD, NekDouble > tmpfieldcoeffs (m_fields[0]->GetNcoeffs()/2);
m_pressure->GetPlane(0)->BwdTrans_IterPerExp(m_pressure->GetPlane(0)->GetCoeffs(), m_pressure->GetPlane(0)->UpdatePhys());
m_pressure->GetPlane(1)->BwdTrans_IterPerExp(m_pressure->GetPlane(1)->GetCoeffs(), m_pressure->GetPlane(1)->UpdatePhys());
m_fields[0]->GetPlane(0)->FwdTrans_IterPerExp(m_pressure->GetPlane(0)->GetPhys(),fieldcoeffs[i]);
m_fields[0]->GetPlane(1)->FwdTrans_IterPerExp(m_pressure->GetPlane(1)->GetPhys(),tmpfieldcoeffs);
for(int e=0; e<m_fields[0]->GetNcoeffs()/2; e++)
{
fieldcoeffs[i][e+m_fields[0]->GetNcoeffs()/2] = tmpfieldcoeffs[e];
}
}
else
{
m_pressure->BwdTrans_IterPerExp(m_pressure->GetCoeffs(),m_pressure->UpdatePhys());
m_fields[0]->FwdTrans_IterPerExp(m_pressure->GetPhys(),fieldcoeffs[i]);
}
variables[i] = "p";
std::string outname = m_sessionName + ".fld";
WriteFld(outname,m_fields[0],fieldcoeffs,variables);
}
void Nektar::CoupledLinearNS::v_TransCoeffToPhys ( void  )
privatevirtual

Definition at line 1406 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::m_fields.

{
int nfields = m_fields.num_elements();
for (int k=0 ; k < nfields; ++k)
{
//Backward Transformation in physical space for time evolution
m_fields[k]->BwdTrans_IterPerExp(m_fields[k]->GetCoeffs(),
m_fields[k]->UpdatePhys());
}
}
void Nektar::CoupledLinearNS::v_TransPhysToCoeff ( void  )
privatevirtual

Definition at line 1418 of file CoupledLinearNS.cpp.

References Nektar::SolverUtils::EquationSystem::m_fields.

{
int nfields = m_fields.num_elements();
for (int k=0 ; k < nfields; ++k)
{
//Forward Transformation in physical space for time evolution
m_fields[k]->FwdTrans_IterPerExp(m_fields[k]->GetPhys(),
m_fields[k]->UpdateCoeffs());
}
}

Friends And Related Function Documentation

friend class MemoryManager< CoupledLinearNS >
friend

Definition at line 92 of file CoupledLinearNS.h.

Member Data Documentation

string Nektar::CoupledLinearNS::className = SolverUtils::GetEquationSystemFactory().RegisterCreatorFunction("CoupledLinearisedNS", CoupledLinearNS::create)
static

Name of class.

Definition at line 103 of file CoupledLinearNS.h.

int Nektar::CoupledLinearNS::m_counter
private

Definition at line 174 of file CoupledLinearNS.h.

Referenced by SolveSteadyNavierStokes(), and v_DoInitialise().

Array<OneD, Array<OneD, NekDouble> > Nektar::CoupledLinearNS::m_ForcingTerm

Definition at line 158 of file CoupledLinearNS.h.

Referenced by DefineForcingTerm(), and EvaluateNewtonRHS().

Array<OneD, Array<OneD, NekDouble> > Nektar::CoupledLinearNS::m_ForcingTerm_Coeffs

Definition at line 159 of file CoupledLinearNS.h.

Referenced by DefineForcingTerm().

bool Nektar::CoupledLinearNS::m_initialStep
private

Definition at line 175 of file CoupledLinearNS.h.

Referenced by SolveLinearNS(), SolveSteadyNavierStokes(), and v_DoInitialise().

NekDouble Nektar::CoupledLinearNS::m_kinvisMin
private

Definition at line 180 of file CoupledLinearNS.h.

Referenced by v_DoInitialise(), and v_DoSolve().

NekDouble Nektar::CoupledLinearNS::m_KinvisPercentage
private

Definition at line 182 of file CoupledLinearNS.h.

Referenced by Continuation(), and v_DoInitialise().

NekDouble Nektar::CoupledLinearNS::m_kinvisStep
private

Definition at line 181 of file CoupledLinearNS.h.

Array<OneD, CoupledLocalToGlobalC0ContMapSharedPtr> Nektar::CoupledLinearNS::m_locToGloMap

Definition at line 161 of file CoupledLinearNS.h.

Referenced by SetUpCoupledMatrix(), SolveLinearNS(), and v_InitObject().

Array<OneD, CoupledSolverMatrices> Nektar::CoupledLinearNS::m_mat
private

Definition at line 187 of file CoupledLinearNS.h.

Referenced by SetUpCoupledMatrix(), and SolveLinearNS().

int Nektar::CoupledLinearNS::m_MatrixSetUpStep
private

Definition at line 179 of file CoupledLinearNS.h.

Referenced by SolveSteadyNavierStokes(), and v_DoInitialise().

int Nektar::CoupledLinearNS::m_maxIt
private

Definition at line 177 of file CoupledLinearNS.h.

Referenced by v_DoInitialise().

int Nektar::CoupledLinearNS::m_Restart
private

Definition at line 178 of file CoupledLinearNS.h.

Referenced by v_DoInitialise().

bool Nektar::CoupledLinearNS::m_singleMode
private

Identify if a single mode is required for stability analysis.

Definition at line 170 of file CoupledLinearNS.h.

Referenced by SetUpCoupledMatrix(), Solve(), SolveLinearNS(), v_InitObject(), and v_Output().

NekDouble Nektar::CoupledLinearNS::m_tol
private

Definition at line 176 of file CoupledLinearNS.h.

Referenced by SolveSteadyNavierStokes(), and v_DoInitialise().

bool Nektar::CoupledLinearNS::m_zeroMode
private

Id to identify when single mode is mean mode (i.e. beta=0);.

Definition at line 172 of file CoupledLinearNS.h.

Referenced by SetUpCoupledMatrix(), and v_InitObject().

Generated on Wed Mar 4 2015 16:33:34 for Nektar++ by   doxygen 1.8.1.2