Nektar++
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
Public Member Functions | Protected Member Functions | Protected Attributes | Private Member Functions | List of all members
Nektar::PulseWaveSystem Class Reference

Base class for unsteady solvers. More...

#include <PulseWaveSystem.h>

Inheritance diagram for Nektar::PulseWaveSystem:
Inheritance graph
[legend]
Collaboration diagram for Nektar::PulseWaveSystem:
Collaboration graph
[legend]

Public Member Functions

virtual ~PulseWaveSystem ()
 Destructor.
int GetNdomains ()
Array< OneD,
MultiRegions::ExpListSharedPtr > 		UpdateVessels (void)
void CalcCharacteristicVariables (int omega)
- Public Member Functions inherited from Nektar::SolverUtils::UnsteadySystem
virtual SOLVER_UTILS_EXPORT ~UnsteadySystem ()
 Destructor.
SOLVER_UTILS_EXPORT NekDouble GetTimeStep (const Array< OneD, const Array< OneD, NekDouble > > &inarray)
 Calculate the larger time-step mantaining the problem stable.
- Public Member Functions inherited from Nektar::SolverUtils::EquationSystem
virtual SOLVER_UTILS_EXPORT ~EquationSystem ()
 Destructor.
SOLVER_UTILS_EXPORT void SetUpTraceNormals (void)
SOLVER_UTILS_EXPORT void InitObject ()
 Initialises the members of this object.
SOLVER_UTILS_EXPORT void DoInitialise ()
 Perform any initialisation necessary before solving the problem.
SOLVER_UTILS_EXPORT void DoSolve ()
 Solve the problem.
SOLVER_UTILS_EXPORT void TransCoeffToPhys ()
 Transform from coefficient to physical space.
SOLVER_UTILS_EXPORT void TransPhysToCoeff ()
 Transform from physical to coefficient space.
SOLVER_UTILS_EXPORT void Output ()
 Perform output operations after solve.
SOLVER_UTILS_EXPORT NekDouble LinfError (unsigned int field, const Array< OneD, NekDouble > &exactsoln=NullNekDouble1DArray)
 Linf error computation.
SOLVER_UTILS_EXPORT std::string GetSessionName ()
 Get Session name.
template<class T >
boost::shared_ptr< T > as ()
SOLVER_UTILS_EXPORT void ResetSessionName (std::string newname)
 Reset Session name.
SOLVER_UTILS_EXPORT
LibUtilities::SessionReaderSharedPtr 		GetSession ()
 Get Session name.
SOLVER_UTILS_EXPORT
MultiRegions::ExpListSharedPtr 		GetPressure ()
 Get pressure field if available.
SOLVER_UTILS_EXPORT void PrintSummary (std::ostream &out)
 Print a summary of parameters and solver characteristics.
SOLVER_UTILS_EXPORT void SetLambda (NekDouble lambda)
 Set parameter m_lambda.
SOLVER_UTILS_EXPORT void EvaluateFunction (Array< OneD, Array< OneD, NekDouble > > &pArray, std::string pFunctionName, const NekDouble pTime=0.0, const int domain=0)
 Evaluates a function as specified in the session file.
SOLVER_UTILS_EXPORT void EvaluateFunction (std::vector< std::string > pFieldNames, Array< OneD, Array< OneD, NekDouble > > &pFields, const std::string &pName, const int domain=0)
 Populate given fields with the function from session.
SOLVER_UTILS_EXPORT void EvaluateFunction (std::vector< std::string > pFieldNames, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields, const std::string &pName, const int domain=0)
 Populate given fields with the function from session.
SOLVER_UTILS_EXPORT void EvaluateFunction (std::string pFieldName, Array< OneD, NekDouble > &pArray, const std::string &pFunctionName, const NekDouble &pTime=0.0, const int domain=0)
SOLVER_UTILS_EXPORT std::string DescribeFunction (std::string pFieldName, const std::string &pFunctionName, const int domain)
 Provide a description of a function for a given field name.
SOLVER_UTILS_EXPORT void InitialiseBaseFlow (Array< OneD, Array< OneD, NekDouble > > &base)
 Perform initialisation of the base flow.
SOLVER_UTILS_EXPORT void SetInitialConditions (NekDouble initialtime=0.0, bool dumpInitialConditions=true, const int domain=0)
 Initialise the data in the dependent fields.
SOLVER_UTILS_EXPORT void EvaluateExactSolution (int field, Array< OneD, NekDouble > &outfield, const NekDouble time)
 Evaluates an exact solution.
SOLVER_UTILS_EXPORT NekDouble L2Error (unsigned int field, const Array< OneD, NekDouble > &exactsoln, bool Normalised=false)
 Compute the L2 error between fields and a given exact solution.
SOLVER_UTILS_EXPORT NekDouble L2Error (unsigned int field, bool Normalised=false)
 Compute the L2 error of the fields.
SOLVER_UTILS_EXPORT Array
< OneD, NekDouble > 		ErrorExtraPoints (unsigned int field)
 Compute error (L2 and L_inf) over an larger set of quadrature points return [L2 Linf].
SOLVER_UTILS_EXPORT void WeakAdvectionGreensDivergenceForm (const Array< OneD, Array< OneD, NekDouble > > &F, Array< OneD, NekDouble > &outarray)
 Compute the inner product 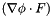$ (\nabla \phi \cdot F) $.
SOLVER_UTILS_EXPORT void WeakAdvectionDivergenceForm (const Array< OneD, Array< OneD, NekDouble > > &F, Array< OneD, NekDouble > &outarray)
 Compute the inner product 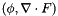$ (\phi, \nabla \cdot F) $.
SOLVER_UTILS_EXPORT void WeakAdvectionNonConservativeForm (const Array< OneD, Array< OneD, NekDouble > > &V, const Array< OneD, const NekDouble > &u, Array< OneD, NekDouble > &outarray, bool UseContCoeffs=false)
 Compute the inner product 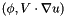$ (\phi, V\cdot \nabla u) $.
f SOLVER_UTILS_EXPORT void AdvectionNonConservativeForm (const Array< OneD, Array< OneD, NekDouble > > &V, const Array< OneD, const NekDouble > &u, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wk=NullNekDouble1DArray)
 Compute the non-conservative advection.
SOLVER_UTILS_EXPORT void WeakDGAdvection (const Array< OneD, Array< OneD, NekDouble > > &InField, Array< OneD, Array< OneD, NekDouble > > &OutField, bool NumericalFluxIncludesNormal=true, bool InFieldIsInPhysSpace=false, int nvariables=0)
 Calculate the weak discontinuous Galerkin advection.
SOLVER_UTILS_EXPORT void WeakDGDiffusion (const Array< OneD, Array< OneD, NekDouble > > &InField, Array< OneD, Array< OneD, NekDouble > > &OutField, bool NumericalFluxIncludesNormal=true, bool InFieldIsInPhysSpace=false)
 Calculate weak DG Diffusion in the LDG form.
SOLVER_UTILS_EXPORT void Checkpoint_Output (const int n)
 Write checkpoint file of m_fields.
SOLVER_UTILS_EXPORT void Checkpoint_Output (const int n, MultiRegions::ExpListSharedPtr &field, std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)
 Write checkpoint file of custom data fields.
SOLVER_UTILS_EXPORT void Checkpoint_BaseFlow (const int n)
 Write base flow file of m_fields.
SOLVER_UTILS_EXPORT void WriteFld (const std::string &outname)
 Write field data to the given filename.
SOLVER_UTILS_EXPORT void WriteFld (const std::string &outname, MultiRegions::ExpListSharedPtr &field, std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)
 Write input fields to the given filename.
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields)
 Input field data from the given file.
SOLVER_UTILS_EXPORT void ImportFldToMultiDomains (const std::string &infile, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields, const int ndomains)
 Input field data from the given file to multiple domains.
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, std::vector< std::string > &fieldStr, Array< OneD, Array< OneD, NekDouble > > &coeffs)
 Output a field. Input field data into array from the given file.
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, MultiRegions::ExpListSharedPtr &pField, std::string &pFieldName)
 Output a field. Input field data into ExpList from the given file.
SOLVER_UTILS_EXPORT void ScanForHistoryPoints ()
 Builds map of which element holds each history point.
SOLVER_UTILS_EXPORT void WriteHistoryData (std::ostream &out)
 Probe each history point and write to file.
SOLVER_UTILS_EXPORT void SessionSummary (SummaryList &vSummary)
 Write out a session summary.
SOLVER_UTILS_EXPORT Array
< OneD,
MultiRegions::ExpListSharedPtr > & 		UpdateFields ()
SOLVER_UTILS_EXPORT
LibUtilities::FieldMetaDataMap & 		UpdateFieldMetaDataMap ()
 Get hold of FieldInfoMap so it can be updated.
SOLVER_UTILS_EXPORT NekDouble GetFinalTime ()
 Return final time.
SOLVER_UTILS_EXPORT int GetNcoeffs ()
SOLVER_UTILS_EXPORT int GetNcoeffs (const int eid)
SOLVER_UTILS_EXPORT int GetNumExpModes ()
SOLVER_UTILS_EXPORT const
Array< OneD, int > 		GetNumExpModesPerExp ()
SOLVER_UTILS_EXPORT int GetNvariables ()
SOLVER_UTILS_EXPORT const
std::string 		GetVariable (unsigned int i)
SOLVER_UTILS_EXPORT int GetTraceTotPoints ()
SOLVER_UTILS_EXPORT int GetTraceNpoints ()
SOLVER_UTILS_EXPORT int GetExpSize ()
SOLVER_UTILS_EXPORT int GetPhys_Offset (int n)
SOLVER_UTILS_EXPORT int GetCoeff_Offset (int n)
SOLVER_UTILS_EXPORT int GetTotPoints ()
SOLVER_UTILS_EXPORT int GetTotPoints (int n)
SOLVER_UTILS_EXPORT int GetNpoints ()
SOLVER_UTILS_EXPORT int GetNumElmVelocity ()
SOLVER_UTILS_EXPORT int GetSteps ()
SOLVER_UTILS_EXPORT NekDouble GetTimeStep ()
SOLVER_UTILS_EXPORT void CopyFromPhysField (const int i, Array< OneD, NekDouble > &output)
SOLVER_UTILS_EXPORT void CopyToPhysField (const int i, Array< OneD, NekDouble > &output)
SOLVER_UTILS_EXPORT void SetStepsToOne ()
SOLVER_UTILS_EXPORT void ZeroPhysFields ()
SOLVER_UTILS_EXPORT void FwdTransFields ()
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &flux)
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &fluxX, Array< OneD, Array< OneD, NekDouble > > &fluxY)
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, const int j, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &flux)
SOLVER_UTILS_EXPORT void NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numflux)
SOLVER_UTILS_EXPORT void NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numfluxX, Array< OneD, Array< OneD, NekDouble > > &numfluxY)
SOLVER_UTILS_EXPORT void NumFluxforScalar (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &uflux)
SOLVER_UTILS_EXPORT void NumFluxforVector (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &qfield, Array< OneD, Array< OneD, NekDouble > > &qflux)
SOLVER_UTILS_EXPORT void SetModifiedBasis (const bool modbasis)
SOLVER_UTILS_EXPORT int NoCaseStringCompare (const string &s1, const string &s2)
 Perform a case-insensitive string comparison.

Protected Member Functions

 PulseWaveSystem (const LibUtilities::SessionReaderSharedPtr &m_session)
 Initialises PulseWaveSystem class members.
virtual void v_InitObject ()
virtual void v_DoInitialise ()
 Sets up initial conditions.
virtual void v_DoSolve ()
 Solves an unsteady problem.
void LinkSubdomains (Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &fields)
 Links the subdomains.
void BifurcationRiemann (Array< OneD, NekDouble > &Au, Array< OneD, NekDouble > &uu, Array< OneD, NekDouble > &beta, Array< OneD, NekDouble > &A_0)
 Riemann Problem for Bifurcation.
void MergingRiemann (Array< OneD, NekDouble > &Au, Array< OneD, NekDouble > &uu, Array< OneD, NekDouble > &beta, Array< OneD, NekDouble > &A_0)
 Riemann Problem for Merging Flow.
void JunctionRiemann (Array< OneD, NekDouble > &Au, Array< OneD, NekDouble > &uu, Array< OneD, NekDouble > &beta, Array< OneD, NekDouble > &A_0)
 Riemann Problem for Junction.
virtual void v_Output (void)
void CheckPoint_Output (const int n)
NekDouble v_L2Error (unsigned int field, const Array< OneD, NekDouble > &exactsoln=NullNekDouble1DArray, bool Normalised=false)
 Compute the L2 error between fields and a given exact solution.
NekDouble v_LinfError (unsigned int field, const Array< OneD, NekDouble > &exactsoln=NullNekDouble1DArray)
 Compute the L_inf error between fields and a given exact solution.
void WriteVessels (const std::string &outname)
 Write input fields to the given filename.
void EnforceInterfaceConditions (const Array< OneD, const Array< OneD, NekDouble > > &fields)
- Protected Member Functions inherited from Nektar::SolverUtils::UnsteadySystem
SOLVER_UTILS_EXPORT UnsteadySystem (const LibUtilities::SessionReaderSharedPtr &pSession)
 Initialises UnsteadySystem class members.
SOLVER_UTILS_EXPORT NekDouble MaxTimeStepEstimator ()
 Get the maximum timestep estimator for cfl control.
virtual SOLVER_UTILS_EXPORT void v_GenerateSummary (SummaryList &s)
 Print a summary of time stepping parameters.
virtual SOLVER_UTILS_EXPORT void v_AppendOutput1D (Array< OneD, Array< OneD, NekDouble > > &solution1D)
 Print the solution at each solution point in a txt file.
virtual SOLVER_UTILS_EXPORT void v_NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numflux)
virtual SOLVER_UTILS_EXPORT void v_NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numfluxX, Array< OneD, Array< OneD, NekDouble > > &numfluxY)
virtual SOLVER_UTILS_EXPORT void v_NumFluxforScalar (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &uflux)
virtual SOLVER_UTILS_EXPORT void v_NumFluxforVector (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &qfield, Array< OneD, Array< OneD, NekDouble > > &qflux)
virtual SOLVER_UTILS_EXPORT
NekDouble 		v_GetTimeStep (const Array< OneD, const Array< OneD, NekDouble > > &inarray)
 Return the timestep to be used for the next step in the time-marching loop.
virtual SOLVER_UTILS_EXPORT bool v_PreIntegrate (int step)
virtual SOLVER_UTILS_EXPORT bool v_PostIntegrate (int step)
SOLVER_UTILS_EXPORT void CheckForRestartTime (NekDouble &time)
- Protected Member Functions inherited from Nektar::SolverUtils::EquationSystem
SOLVER_UTILS_EXPORT EquationSystem (const LibUtilities::SessionReaderSharedPtr &pSession)
 Initialises EquationSystem class members.
int nocase_cmp (const string &s1, const string &s2)
SOLVER_UTILS_EXPORT void SetBoundaryConditions (NekDouble time)
 Evaluates the boundary conditions at the given time.
virtual SOLVER_UTILS_EXPORT void v_TransCoeffToPhys ()
 Virtual function for transformation to physical space.
virtual SOLVER_UTILS_EXPORT void v_TransPhysToCoeff ()
 Virtual function for transformation to coefficient space.
virtual SOLVER_UTILS_EXPORT void v_SetInitialConditions (NekDouble initialtime=0.0, bool dumpInitialConditions=true, const int domain=0)
virtual SOLVER_UTILS_EXPORT void v_EvaluateExactSolution (unsigned int field, Array< OneD, NekDouble > &outfield, const NekDouble time)
SOLVER_UTILS_EXPORT void SetUpBaseFields (SpatialDomains::MeshGraphSharedPtr &mesh)
SOLVER_UTILS_EXPORT void ImportFldBase (std::string pInfile, SpatialDomains::MeshGraphSharedPtr pGraph)
virtual SOLVER_UTILS_EXPORT
MultiRegions::ExpListSharedPtr 		v_GetPressure (void)
virtual SOLVER_UTILS_EXPORT void v_ExtraFldOutput (std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)

Protected Attributes

Array< OneD,
MultiRegions::ExpListSharedPtr > 		m_vessels
int m_nDomains
int m_currentDomain
int m_nVariables
UpwindTypePulse m_upwindTypePulse
Array< OneD, int > m_fieldPhysOffset
NekDouble m_rho
NekDouble m_pext
NekDouble m_C
NekDouble m_RT
NekDouble m_pout
Array< OneD, Array< OneD,
NekDouble > > 		m_A_0
Array< OneD, Array< OneD,
NekDouble > > 		m_A_0_trace
Array< OneD, Array< OneD,
NekDouble > > 		m_beta
Array< OneD, Array< OneD,
NekDouble > > 		m_beta_trace
Array< OneD, Array< OneD,
NekDouble > > 		m_trace_fwd_normal
std::vector< std::vector
< InterfacePointShPtr > > 		m_vesselJcts
std::vector< std::vector
< InterfacePointShPtr > > 		m_bifurcations
std::vector< std::vector
< InterfacePointShPtr > > 		m_mergingJcts
- Protected Attributes inherited from Nektar::SolverUtils::UnsteadySystem
int m_infosteps
 Number of time steps between outputting status information.
LibUtilities::TimeIntegrationWrapperSharedPtr m_intScheme
 Wrapper to the time integration scheme.
LibUtilities::TimeIntegrationSchemeOperators m_ode
 The time integration scheme operators to use.
LibUtilities::TimeIntegrationSolutionSharedPtr m_intSoln
NekDouble m_epsilon
bool m_explicitDiffusion
 Indicates if explicit or implicit treatment of diffusion is used.
bool m_explicitAdvection
 Indicates if explicit or implicit treatment of advection is used.
bool m_explicitReaction
 Indicates if explicit or implicit treatment of reaction is used.
bool m_homoInitialFwd
 Flag to determine if simulation should start in homogeneous forward transformed state.
std::vector< int > m_intVariables
std::vector< FilterSharedPtr > m_filters
- Protected Attributes inherited from Nektar::SolverUtils::EquationSystem
LibUtilities::CommSharedPtr m_comm
 Communicator.
LibUtilities::SessionReaderSharedPtr m_session
 The session reader.
LibUtilities::FieldIOSharedPtr m_fld
 Field input/output.
Array< OneD,
MultiRegions::ExpListSharedPtr > 		m_fields
 Array holding all dependent variables.
Array< OneD,
MultiRegions::ExpListSharedPtr > 		m_base
 Base fields.
Array< OneD,
MultiRegions::ExpListSharedPtr > 		m_derivedfields
 Array holding all dependent variables.
SpatialDomains::BoundaryConditionsSharedPtr m_boundaryConditions
 Pointer to boundary conditions object.
SpatialDomains::MeshGraphSharedPtr m_graph
 Pointer to graph defining mesh.
std::string m_sessionName
 Name of the session.
NekDouble m_time
 Current time of simulation.
NekDouble m_fintime
 Finish time of the simulation.
NekDouble m_timestep
 Time step size.
NekDouble m_lambda
 Lambda constant in real system if one required.
NekDouble m_checktime
 Time between checkpoints.
int m_steps
 Number of steps to take.
int m_checksteps
 Number of steps between checkpoints.
int m_spacedim
 Spatial dimension (>= expansion dim).
int m_expdim
 Expansion dimension.
bool m_SingleMode
 Flag to determine if single homogeneous mode is used.
bool m_HalfMode
 Flag to determine if half homogeneous mode is used.
bool m_MultipleModes
 Flag to determine if use multiple homogenenous modes are used.
bool m_useFFT
 Flag to determine if FFT is used for homogeneous transform.
bool m_homogen_dealiasing
 Flag to determine if dealiasing is used for homogeneous simulations.
bool m_specHP_dealiasing
 Flag to determine if dealisising is usde for the Spectral/hp element discretisation.
enum MultiRegions::ProjectionType m_projectionType
 Type of projection; e.g continuous or discontinuous.
Array< OneD, Array< OneD,
NekDouble > > 		m_traceNormals
 Array holding trace normals for DG simulations in the forwards direction.
Array< OneD, Array< OneD,
Array< OneD, NekDouble > > > 		m_gradtan
 1 x nvariable x nq
Array< OneD, Array< OneD,
Array< OneD, NekDouble > > > 		m_tanbasis
 2 x m_spacedim x nq
Array< OneD, bool > m_checkIfSystemSingular
 Flag to indicate if the fields should be checked for singularity.
LibUtilities::FieldMetaDataMap m_fieldMetaDataMap
 Map to identify relevant solver info to dump in output fields.
int m_NumQuadPointsError
 Number of Quadrature points used to work out the error.
enum HomogeneousType m_HomogeneousType
NekDouble m_LhomX
 physical length in X direction (if homogeneous)
NekDouble m_LhomY
 physical length in Y direction (if homogeneous)
NekDouble m_LhomZ
 physical length in Z direction (if homogeneous)
int m_npointsX
 number of points in X direction (if homogeneous)
int m_npointsY
 number of points in Y direction (if homogeneous)
int m_npointsZ
 number of points in Z direction (if homogeneous)
int m_HomoDirec
 number of homogenous directions
int m_NumMode
 Mode to use in case of single mode analysis.

Private Member Functions

void SetUpDomainInterfaces (void)
void FillDataFromInterfacePoint (InterfacePointShPtr &I, const Array< OneD, const Array< OneD, NekDouble > > &field, NekDouble &A, NekDouble &u, NekDouble &beta, NekDouble &A_0)

Additional Inherited Members

- Public Attributes inherited from Nektar::SolverUtils::UnsteadySystem
NekDouble m_cflSafetyFactor
 CFL safety factor (comprise between 0 to 1).
- Protected Types inherited from Nektar::SolverUtils::EquationSystem
enum  HomogeneousType { eHomogeneous1D, eHomogeneous2D, eHomogeneous3D, eNotHomogeneous }
 Parameter for homogeneous expansions. More...

Detailed Description

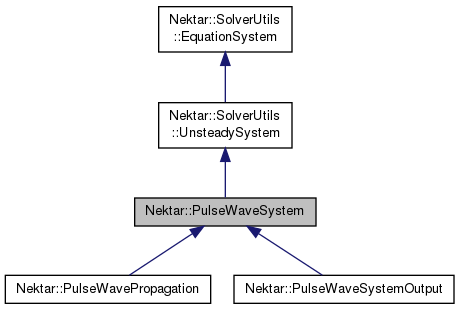
Base class for unsteady solvers.

Initialises the arterial subdomains in m_vessels and sets up all domain-linking conditions (bifurcations, junctions, merging flows). Detects the network structure and assigns boundary conditons. Also provides the underlying timestepping framework for pulse wave solvers including the general timestepping routines.

Definition at line 86 of file PulseWaveSystem.h.

Constructor & Destructor Documentation

Nektar::PulseWaveSystem::~PulseWaveSystem ( )
virtual

Destructor.

Destructor

Definition at line 72 of file PulseWaveSystem.cpp.

{
}
Nektar::PulseWaveSystem::PulseWaveSystem ( const LibUtilities::SessionReaderSharedPtr &  m_session)
protected

Initialises PulseWaveSystem class members.

Processes SolverInfo parameters from the session file and sets up timestepping-specific code.

Parameters
m_SessionSession object to read parameters from.

Definition at line 64 of file PulseWaveSystem.cpp.

: UnsteadySystem(m_session)
{
}

Member Function Documentation

void Nektar::PulseWaveSystem::BifurcationRiemann ( Array< OneD, NekDouble > &  Au,
Array< OneD, NekDouble > &  uu,
Array< OneD, NekDouble > &  beta,
Array< OneD, NekDouble > &  A_0 
)
protected

Riemann Problem for Bifurcation.

Solves the Riemann problem at a bifurcation by assuming subsonic flow at both sides of the boundary and by applying conservation of mass and continuity of the total pressure 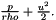$ \frac{p}{rho} + \frac{u^{2}}{2}. $ The other 3 missing equations come from the characteristic variables. For further information see "Pulse WavePropagation in the human vascular system" Section 3.4.4

Definition at line 652 of file PulseWaveSystem.cpp.

References ASSERTL0, and m_rho.

Referenced by EnforceInterfaceConditions().

{
NekDouble rho = m_rho;
Array<OneD, NekDouble> W(3);
Array<OneD, NekDouble> W_Au(3);
Array<OneD, NekDouble> P_Au(3);
Array<OneD, NekDouble> f(6);
Array<OneD, NekDouble> g(6);
Array<OneD, NekDouble> tmp(6);
Array<OneD, Array<OneD, NekDouble> > inv_J(6);
for (int i=0; i<6; i++)
{
inv_J[i] = Array<OneD, NekDouble> (6);
}
NekDouble k = 0.0;
NekDouble k1 = 0.0;
NekDouble k2 = 0.0;
NekDouble k3 = 0.0;
int proceed = 1;
int iter = 0;
int MAX_ITER = 7;
// Calculated from input
W[0] = uu[0] + 4*sqrt(beta[0]/(2*rho))*(sqrt(sqrt(Au[0])) - sqrt(sqrt(A_0[0])));
W[1] = uu[1] - 4*sqrt(beta[1]/(2*rho))*(sqrt(sqrt(Au[1])) - sqrt(sqrt(A_0[1])));
W[2] = uu[2] - 4*sqrt(beta[2]/(2*rho))*(sqrt(sqrt(Au[2])) - sqrt(sqrt(A_0[2])));
// Tolerances for the algorithm
NekDouble Tol = 1.0e-10;
// Newton Iteration
while ((proceed) && (iter < MAX_ITER))
{
iter = iter+1;
// Calculate the constraint vector, six equations:
// 3 characteristic variables, mass conservation,
// total pressure
W_Au[0] = 4*sqrt(beta[0]/(2*rho))*(sqrt(sqrt(Au[0])) - sqrt(sqrt(A_0[0])));
W_Au[1] = 4*sqrt(beta[1]/(2*rho))*(sqrt(sqrt(Au[1])) - sqrt(sqrt(A_0[1])));
W_Au[2] = 4*sqrt(beta[2]/(2*rho))*(sqrt(sqrt(Au[2])) - sqrt(sqrt(A_0[2])));
P_Au[0] = beta[0]*(sqrt(Au[0]) - sqrt(A_0[0]));
P_Au[1] = beta[1]*(sqrt(Au[1]) - sqrt(A_0[1]));
P_Au[2] = beta[2]*(sqrt(Au[2]) - sqrt(A_0[2]));
f[0] = uu[0] + W_Au[0] - W[0];
f[1] = uu[1] - W_Au[1] - W[1];
f[2] = uu[2] - W_Au[2] - W[2];
f[3] = Au[0]*uu[0] - Au[1]*uu[1] - Au[2]*uu[2];
f[4] = uu[0]*uu[0] + 2.0/rho*P_Au[0] - uu[1]*uu[1] - 2.0/rho*P_Au[1];
f[5] = uu[0]*uu[0] + 2.0/rho*P_Au[0] - uu[2]*uu[2] - 2.0/rho*P_Au[2];
// Calculate the wave speed at each vessel
NekDouble c1 = sqrt(beta[0]/(2*rho))*sqrt(sqrt(Au[0]));
NekDouble c2 = sqrt(beta[1]/(2*rho))*sqrt(sqrt(Au[1]));
NekDouble c3 = sqrt(beta[2]/(2*rho))*sqrt(sqrt(Au[2]));
// Inverse Jacobian matrix J(x[n])^(-1), is
// already inverted here analytically
k = c1*Au[1]*c3+Au[0]*c3*c2+Au[2]*c1*c2;
k1 = (c1-uu[0])*k;
inv_J[0][0] = (-c2*uu[0]*c3*Au[0]+Au[2]*c2*c1*c1+Au[1]*c1*c1*c3)/k1;
inv_J[0][1] = Au[1]*(c2-uu[1])*c1*c3/k1;
inv_J[0][2] = Au[2]*(c3-uu[2])*c1*c2/k1;
inv_J[0][3] = c1*c2*c3/k1;
inv_J[0][4] = -0.5*c1*Au[1]*c3/k1;
inv_J[0][5] = -0.5*Au[2]*c1*c2/k1;
k2 = (c2+uu[1])*k;
inv_J[1][0] = Au[0]*(c1+uu[0])*c2*c3/k2;
inv_J[1][1] = (c1*uu[1]*c3*Au[1]+Au[2]*c1*c2*c2+c3*c2*c2*Au[0])/k2;
inv_J[1][2] = -Au[2]*(c3-uu[2])*c1*c2/k2;
inv_J[1][3] = -c1*c2*c3/k2;
inv_J[1][4] = -0.5*(c1*Au[2]+Au[0]*c3)*c2/k2;
inv_J[1][5] = 0.5*Au[2]*c1*c2/k2;
k3 = (c3+uu[2])*k;
inv_J[2][0] = Au[0]*(c1+uu[0])*c2*c3/k3;
inv_J[2][1] = -Au[1]*(c2-uu[1])*c1*c3/k3;
inv_J[2][2] = (c1*c2*uu[2]*Au[2]+c1*Au[1]*c3*c3+c2*c3*c3*Au[0])/k3;
inv_J[2][3] = -c1*c2*c3/k3;
inv_J[2][4] = 0.5*c1*Au[1]*c3/k3;
inv_J[2][5] = -0.5*(Au[1]*c1+c2*Au[0])*c3/k3;
inv_J[3][0] = Au[0]*(Au[0]*c3*c2-uu[0]*c3*Au[1]-uu[0]*c2*Au[2])/k1;
inv_J[3][1] = -Au[0]*Au[1]*(c2-uu[1])*c3/k1;
inv_J[3][2] = -Au[0]*Au[2]*(c3-uu[2])*c2/k1;
inv_J[3][3] = -Au[0]*c3*c2/k1;
inv_J[3][4] = 0.5*Au[0]*Au[1]*c3/k1;
inv_J[3][5] = 0.5*Au[0]*c2*Au[2]/k1;
inv_J[4][0] = Au[0]*Au[1]*(c1+uu[0])*c3/k2;
inv_J[4][1] = -Au[1]*(c1*Au[1]*c3+c1*uu[1]*Au[2]+c3*uu[1]*Au[0])/k2;
inv_J[4][2] = -Au[2]*Au[1]*(c3-uu[2])*c1/k2;
inv_J[4][3] = -c1*Au[1]*c3/k2;
inv_J[4][4] = -0.5*Au[1]*(c1*Au[2]+Au[0]*c3)/k2;
inv_J[4][5] = 0.5*Au[2]*Au[1]*c1/k2;
inv_J[5][0] = Au[0]*Au[2]*(c1+uu[0])*c2/k3;
inv_J[5][1] = -Au[2]*Au[1]*(c2-uu[1])*c1/k3;
inv_J[5][2] = -Au[2]*(Au[2]*c1*c2+c1*uu[2]*Au[1]+c2*uu[2]*Au[0])/k3;
inv_J[5][3] = -Au[2]*c1*c2/k3;
inv_J[5][4] = 0.5*Au[2]*Au[1]*c1/k3;
inv_J[5][5] = -0.5*Au[2]*(Au[1]*c1+c2*Au[0])/k3;
// Solve the system by multiplying the Jacobian with the vector f:
// g = (inv_J)*f
for (int j=0; j<6; j++)
{
tmp[j] =0.0;
g[j] = 0.0;
}
for (int j=0; j<6; j++)
{
for (int i=0; i<6; i++)
{
tmp[j] = inv_J[j][i]*f[i];
g[j] += tmp[j];
}
}
// Update the solution: x_new = x_old - dx
uu[0] = uu[0] - g[0];
uu[1] = uu[1] - g[1];
uu[2] = uu[2] - g[2];
Au[0] = Au[0] - g[3];
Au[1] = Au[1] - g[4];
Au[2] = Au[2] - g[5];
// Check if the error of the solution is smaller than Tol
if ((g[0]*g[0] + g[1]*g[1] + g[2]*g[2] + g[3]*g[3]+ g[4]*g[4] + g[5]*g[5]) < Tol)
{
proceed = 0;
}
// Check if solver converges
if (iter >= MAX_ITER)
{
ASSERTL0(false,"Riemann solver for Bifurcation did not converge");
}
}
}
void Nektar::PulseWaveSystem::CalcCharacteristicVariables ( int  omega)

Definition at line 1291 of file PulseWaveSystem.cpp.

References m_beta, m_rho, m_vessels, Vmath::Smul(), Vmath::Vadd(), Vmath::Vmul(), Vmath::Vsqrt(), and Vmath::Vsub().

{
int nq = m_vessels[omega]->GetTotPoints();
Array<OneD, NekDouble> A = m_vessels[omega]->UpdatePhys();
Array<OneD, NekDouble> u = m_vessels[omega+1]->UpdatePhys();
Array<OneD, NekDouble> c(nq);
//Calc 4*c
Vmath::Vsqrt(nq,A,1,c,1);
Vmath::Vmul(nq,m_beta[omega],1,c,1,c,1);
Vmath::Smul(nq,16.0/(2*m_rho),c,1,c,1);
Vmath::Vsqrt(nq,c,1,c,1);
// Characteristics
Vmath::Vadd(nq,u,1,c,1,A,1);
Vmath::Vsub(nq,u,1,c,1,u,1);
}
void Nektar::PulseWaveSystem::CheckPoint_Output ( const int  n)
protected

Writes the .fld file at the end of the simulation. Similar to the normal v_Output however the Multidomain output has to be prepared.

Definition at line 1098 of file PulseWaveSystem.cpp.

References Nektar::SolverUtils::EquationSystem::m_sessionName, and WriteVessels().

Referenced by v_DoSolve().

{
std::stringstream outname;
outname << m_sessionName << "_" << n << ".chk";
WriteVessels(outname.str());
}
void Nektar::PulseWaveSystem::EnforceInterfaceConditions ( const Array< OneD, const Array< OneD, NekDouble > > &  fields)
protected

Definition at line 563 of file PulseWaveSystem.cpp.

References BifurcationRiemann(), FillDataFromInterfacePoint(), JunctionRiemann(), m_bifurcations, m_mergingJcts, m_nVariables, m_vesselJcts, m_vessels, and MergingRiemann().

Referenced by Nektar::PulseWavePropagation::DoOdeRhs().

{
int dom, bcpos;
Array<OneD, NekDouble> Au(3),uu(3),beta(3),A_0(3);
// Enfore Bifurcations;
for(int n = 0; n < m_bifurcations.size(); ++n)
{
FillDataFromInterfacePoint(m_bifurcations[n][0],fields,
Au[0],uu[0],beta[0],A_0[0]);
FillDataFromInterfacePoint(m_bifurcations[n][1],fields,
Au[1],uu[1],beta[1],A_0[1]);
FillDataFromInterfacePoint(m_bifurcations[n][2],fields,
Au[2],uu[2],beta[2],A_0[2]);
// Solve the Riemann problem for a bifurcation
BifurcationRiemann(Au, uu, beta, A_0);
// Store the values into the right positions:
for(int i = 0; i < 3; ++i)
{
dom = m_bifurcations[n][i]->m_domain;
bcpos = m_bifurcations[n][i]->m_bcPosition;
m_vessels[dom*m_nVariables] ->UpdateBndCondExpansion(bcpos)->UpdatePhys()[0] = Au[i];
m_vessels[dom*m_nVariables+1]->UpdateBndCondExpansion(bcpos)->UpdatePhys()[0] = uu[i];
}
}
// Enfore Bifurcations;
for(int n = 0; n < m_mergingJcts.size(); ++n)
{
// Merged vessel
FillDataFromInterfacePoint(m_mergingJcts[n][0],fields,
Au[0],uu[0],beta[0],A_0[0]);
FillDataFromInterfacePoint(m_mergingJcts[n][1],fields,
Au[1],uu[1],beta[1],A_0[1]);
FillDataFromInterfacePoint(m_mergingJcts[n][2],fields,
Au[2],uu[2],beta[2],A_0[2]);
// Solve the Riemann problem for a merging vessel
MergingRiemann(Au, uu, beta, A_0);
// Store the values into the right positions:
for(int i = 0; i < 3; ++i)
{
int dom = m_mergingJcts[n][i]->m_domain;
int bcpos = m_mergingJcts[n][i]->m_bcPosition;
m_vessels[dom*m_nVariables] ->UpdateBndCondExpansion(bcpos)->UpdatePhys()[0] = Au[i];
m_vessels[dom*m_nVariables+1]->UpdateBndCondExpansion(bcpos)->UpdatePhys()[0] = uu[i];
}
}
for(int n = 0; n < m_vesselJcts.size(); ++n)
{
FillDataFromInterfacePoint(m_vesselJcts[n][0],fields,
Au[0],uu[0],beta[0],A_0[0]);
FillDataFromInterfacePoint(m_vesselJcts[n][1],fields,
Au[1],uu[1],beta[1],A_0[1]);
JunctionRiemann(Au, uu, beta, A_0);
// Store the values into the right positions:
for(int i = 0; i < 2; ++i)
{
int dom = m_vesselJcts[n][i]->m_domain;
int bcpos = m_vesselJcts[n][i]->m_bcPosition;
m_vessels[dom*m_nVariables] ->UpdateBndCondExpansion(bcpos)->UpdatePhys()[0] = Au[i];
m_vessels[dom*m_nVariables+1]->UpdateBndCondExpansion(bcpos)->UpdatePhys()[0] = uu[i];
//cout<<"Au: "<<Au[i]<<endl;
//cout<<"uu: "<<uu[i]<<endl;
//cout<<endl;
}
}
}
void Nektar::PulseWaveSystem::FillDataFromInterfacePoint ( InterfacePointShPtr &  I,
const Array< OneD, const Array< OneD, NekDouble > > &  field,
NekDouble &  A,
NekDouble &  u,
NekDouble &  beta,
NekDouble &  A_0 
)
private

Definition at line 537 of file PulseWaveSystem.cpp.

References m_A_0_trace, m_beta_trace, m_fieldPhysOffset, m_nVariables, and m_vessels.

Referenced by EnforceInterfaceConditions().

{
int omega, traceId, eid, vert, phys_offset, vesselID;
// Parent vessel
omega = I->m_domain;
traceId = I->m_traceId;
eid = I->m_elmt;
vert = I->m_elmtVert;
vesselID = omega*m_nVariables;
phys_offset = m_vessels[vesselID]->GetPhys_Offset(eid);
m_vessels[vesselID]->GetExp(eid)->
GetVertexPhysVals(vert, fields[0]+m_fieldPhysOffset[omega]+phys_offset, A);
m_vessels[vesselID]->GetExp(eid)->
GetVertexPhysVals(vert, fields[1]+m_fieldPhysOffset[omega]+phys_offset, u);
beta = m_beta_trace[omega][traceId];
A_0 = m_A_0_trace [omega][traceId];
}
int Nektar::PulseWaveSystem::GetNdomains ( )
inline

Definition at line 92 of file PulseWaveSystem.h.

{
return m_nDomains;
}
void Nektar::PulseWaveSystem::JunctionRiemann ( Array< OneD, NekDouble > &  Au,
Array< OneD, NekDouble > &  uu,
Array< OneD, NekDouble > &  beta,
Array< OneD, NekDouble > &  A_0 
)
protected

Riemann Problem for Junction.

Solves the Riemann problem at an interdomain junction by assuming subsonic flow at both sides of the boundary and by applying conservation of mass and continuity of the total pressure 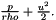$ \frac{p}{rho} + \frac{u^{2}}{2}. $ The other 2 missing equations come from the characteristic variables. For further information see "Pulse WavePropagation in the human vascular system" Section 3.4.

Definition at line 968 of file PulseWaveSystem.cpp.

References ASSERTL0, and m_rho.

Referenced by EnforceInterfaceConditions().

{
NekDouble rho = m_rho;
Array<OneD, NekDouble> W(2);
Array<OneD, NekDouble> W_Au(2);
Array<OneD, NekDouble> P_Au(2);
Array<OneD, NekDouble> f(4);
Array<OneD, NekDouble> g(4);
Array<OneD, NekDouble> tmp(4);
Array<OneD, Array<OneD, NekDouble> > inv_J(4);
for (int i=0; i<4; i++)
{
inv_J[i] = Array<OneD, NekDouble> (4);
}
NekDouble k = 0.0;
NekDouble k1 = 0.0;
NekDouble k2 = 0.0;
int proceed = 1;
int iter = 0;
int MAX_ITER = 7;
NekDouble Tol = 1.0e-10;
// Calculated from input
W[0] = uu[0] + 4*sqrt(beta[0]/(2*rho))*(sqrt(sqrt(Au[0])) - sqrt(sqrt(A_0[0])));
W[1] = uu[1] - 4*sqrt(beta[1]/(2*rho))*(sqrt(sqrt(Au[1])) - sqrt(sqrt(A_0[1])));
while((proceed) && (iter < MAX_ITER))
{
iter = iter+1;
// Calculate the constraint vector, 4 equations:
// 2 characteristic variables, mass conservation,
// total pressure
W_Au[0] = 4*sqrt(beta[0]/(2*rho))*(sqrt(sqrt(Au[0])) - sqrt(sqrt(A_0[0])));
W_Au[1] = 4*sqrt(beta[1]/(2*rho))*(sqrt(sqrt(Au[1])) - sqrt(sqrt(A_0[1])));
P_Au[0] = beta[0]*(sqrt(Au[0]) - sqrt(A_0[0]));
P_Au[1] = beta[1]*(sqrt(Au[1]) - sqrt(A_0[1]));
f[0] = uu[0] + W_Au[0] - W[0];
f[1] = uu[1] - W_Au[1] - W[1];
f[2] = Au[0]*uu[0] - Au[1]*uu[1];
f[3] = uu[0]*uu[0] + 2.0/rho*P_Au[0] - uu[1]*uu[1] - 2.0/rho*P_Au[1];
// Calculate the wave speed at each vessel
NekDouble cl = sqrt(beta[0]/(2*rho))*sqrt(sqrt(Au[0]));
NekDouble cr = sqrt(beta[1]/(2*rho))*sqrt(sqrt(Au[1]));
// Inverse Jacobian matrix J(x[n])^(-1), is already inverted here analytically
k = (cl*Au[1]+Au[0]*cr);
k1 = (cl-uu[0])*k;
inv_J[0][0] = (Au[1]*cl*cl-cr*uu[0]*Au[0])/k1;
inv_J[0][1] = Au[1]*(cr-uu[1])*cl/k1;
inv_J[0][2] = cl*cr/k1;
inv_J[0][3] = -0.5*cl*Au[1]/k1;
k2 = (cr+uu[1])*k;
inv_J[1][0] = Au[0]*(cl+uu[0])*cr/k2;
inv_J[1][1] = (cl*uu[1]*Au[1]+cr*cr*Au[0])/k2;
inv_J[1][2] = -cl*cr/k2;
inv_J[1][3] = -0.5*Au[0]*cr/k2;
inv_J[2][0] = Au[0]*(Au[0]*cr-uu[0]*Au[1])/k1;
inv_J[2][1] = -Au[0]*Au[1]*(cr-uu[1])/k1;
inv_J[2][2] = -Au[0]*cr/k1;
inv_J[2][3] = 0.5*Au[1]*Au[0]/k1;
inv_J[3][0] = Au[0]*Au[1]*(cl+uu[0])/k2;
inv_J[3][1] = -Au[1]*(cl*Au[1]+uu[1]*Au[0])/k2;
inv_J[3][2] = -cl*Au[1]/k2;
inv_J[3][3] = -0.5*Au[1]*Au[0]/k2;
// Solve the system by multiplying the Jacobian with the vector f:
// g = (inv_J)*f
for (int j=0; j<4; j++)
{
tmp[j] =0.0;
g[j] = 0.0;
}
for (int j=0; j<4; j++)
{
for (int i=0; i<4; i++)
{
tmp[j] = inv_J[j][i]*f[i];
g[j] += tmp[j];
}
}
// Update solution: x_new = x_old - dx
uu[0] -= g[0];
uu[1] -= g[1];
Au[0] -= g[2];
Au[1] -= g[3];
// Check if the error of the solution is smaller than Tol.
if((g[0]*g[0] + g[1]*g[1] + g[2]*g[2] + g[3]*g[3]) < Tol)
proceed = 0;
}
if(iter >= MAX_ITER)
{
ASSERTL0(false,"Riemann solver for Junction did not converge");
}
}
void Nektar::PulseWaveSystem::LinkSubdomains ( Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  fields)
protected

Links the subdomains.

void Nektar::PulseWaveSystem::MergingRiemann ( Array< OneD, NekDouble > &  Au,
Array< OneD, NekDouble > &  uu,
Array< OneD, NekDouble > &  beta,
Array< OneD, NekDouble > &  A_0 
)
protected

Riemann Problem for Merging Flow.

Solves the Riemann problem at an merging flow condition by assuming subsonic flow at both sides of the boundary and by applying conservation of mass and continuity of the total pressure 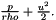$ \frac{p}{rho} + \frac{u^{2}}{2}. $ The other 3 missing equations come from the characteristic variables. For further information see "Pulse WavePropagation in the human vascular system" Section 3.4.4

Definition at line 811 of file PulseWaveSystem.cpp.

References ASSERTL0, and m_rho.

Referenced by EnforceInterfaceConditions().

{
NekDouble rho = m_rho;
Array<OneD, NekDouble> W(3);
Array<OneD, NekDouble> W_Au(3);
Array<OneD, NekDouble> P_Au(3);
Array<OneD, NekDouble> f(6);
Array<OneD, NekDouble> g(6);
Array<OneD, NekDouble> tmp(6);
Array<OneD, Array<OneD, NekDouble> > inv_J(6);
for (int i=0; i<6; i++)
{
inv_J[i] = Array<OneD, NekDouble> (6);
}
NekDouble k = 0.0;
NekDouble k1 = 0.0;
NekDouble k2 = 0.0;
NekDouble k3 = 0.0;
int proceed = 1;
int iter = 0;
int MAX_ITER = 7;
// Calculated from input
W[0] = uu[0] - 4*sqrt(beta[0]/(2*rho))*(sqrt(sqrt(Au[0])) - sqrt(sqrt(A_0[0])));
W[1] = uu[1] + 4*sqrt(beta[1]/(2*rho))*(sqrt(sqrt(Au[1])) - sqrt(sqrt(A_0[1])));
W[2] = uu[2] + 4*sqrt(beta[2]/(2*rho))*(sqrt(sqrt(Au[2])) - sqrt(sqrt(A_0[2])));
// Tolerances for the algorithm
NekDouble Tol = 1.0e-10;
// Newton Iteration
while ((proceed) && (iter < MAX_ITER))
{
iter = iter+1;
// Calculate the constraint vector, six equations:
// 3 characteristic variables, mass conservation,
// total pressure
W_Au[0] = 4*sqrt(beta[0]/(2*rho))*(sqrt(sqrt(Au[0])) - sqrt(sqrt(A_0[0])));
W_Au[1] = 4*sqrt(beta[1]/(2*rho))*(sqrt(sqrt(Au[1])) - sqrt(sqrt(A_0[1])));
W_Au[2] = 4*sqrt(beta[2]/(2*rho))*(sqrt(sqrt(Au[2])) - sqrt(sqrt(A_0[2])));
P_Au[0] = beta[0]*(sqrt(Au[0]) - sqrt(A_0[0]));
P_Au[1] = beta[1]*(sqrt(Au[1]) - sqrt(A_0[1]));
P_Au[2] = beta[2]*(sqrt(Au[2]) - sqrt(A_0[2]));
f[0] = uu[0] - W_Au[0] - W[0];
f[1] = uu[1] + W_Au[1] - W[1];
f[2] = uu[2] + W_Au[2] - W[2];
f[3] = Au[0]*uu[0] - Au[1]*uu[1] - Au[2]*uu[2];
f[4] = uu[0]*uu[0] + 2.0/rho*P_Au[0] - uu[1]*uu[1] - 2.0/rho*P_Au[1];
f[5] = uu[0]*uu[0] + 2.0/rho*P_Au[0] - uu[2]*uu[2] - 2.0/rho*P_Au[2];
// Calculate the wave speed at each vessel
NekDouble c1 = sqrt(beta[0]/(2*rho))*sqrt(sqrt(Au[0]));
NekDouble c2 = sqrt(beta[1]/(2*rho))*sqrt(sqrt(Au[1]));
NekDouble c3 = sqrt(beta[2]/(2*rho))*sqrt(sqrt(Au[2]));
// Inverse Jacobian matrix J(x[n])^(-1), is already inverted here analytically
k = c1*Au[1]*c3+Au[0]*c3*c2+Au[2]*c1*c2;
k1 = (c1+uu[0])*k;
inv_J[0][0] = (c2*uu[0]*c3*Au[0]+Au[2]*c2*c1*c1+Au[1]*c1*c1*c3)/k1;
inv_J[0][1] = Au[1]*(c2+uu[1])*c1*c3/k1;
inv_J[0][2] = Au[2]*(c3+uu[2])*c1*c2/k1;
inv_J[0][3] = c1*c2*c3/k1;
inv_J[0][4] = 0.5*Au[1]*c1*c3/k1;
inv_J[0][5] = 0.5*Au[2]*c1*c2/k1;
k2 = (c2-uu[1])*k;
inv_J[1][0] = Au[0]*(c1-uu[0])*c2*c3/k2;
inv_J[1][1] = (-c1*uu[1]*c3*Au[1]+Au[2]*c1*c2*c2+c3*c2*c2*Au[0])/k2;
inv_J[1][2] = -Au[2]*(c3+uu[2])*c1*c2/k2;
inv_J[1][3] = -c1*c2*c3/k2;
inv_J[1][4] = 0.5*(c1*Au[2]+Au[0]*c3)*c2/k2;
inv_J[1][5] = -0.5*Au[2]*c1*c2/k2;
k3 = (c3-uu[2])*k;
inv_J[2][0] = Au[0]*(c1-uu[0])*c2*c3/k3;
inv_J[2][1] = -Au[1]*(c2+uu[1])*c1*c3/k3;
inv_J[2][2] = -(c1*uu[2]*c2*Au[2]-Au[1]*c1*c3*c3-c2*c3*c3*Au[0])/k3;
inv_J[2][3] = -c1*c2*c3/k3;
inv_J[2][4] = -0.5*Au[1]*c1*c3/k3;
inv_J[2][5] = 0.5*(Au[1]*c1+Au[0]*c2)*c3/k3;
inv_J[3][0] = -Au[0]*(Au[0]*c3*c2+uu[0]*c3*Au[1]+uu[0]*c2*Au[2])/k1;
inv_J[3][1] = Au[0]*Au[1]*(c2+uu[1])*c3/k1;
inv_J[3][2] = Au[0]*Au[2]*(c3+uu[2])*c2/k1;
inv_J[3][3] = Au[0]*c3*c2/k1;
inv_J[3][4] = 0.5*Au[0]*Au[1]*c3/k1;
inv_J[3][5] = 0.5*Au[0]*c2*Au[2]/k1;
inv_J[4][0] = -Au[0]*Au[1]*(c1-uu[0])*c3/k2;
inv_J[4][1] = Au[1]*(Au[1]*c1*c3-c1*uu[1]*Au[2]-c3*uu[1]*Au[0])/k2;
inv_J[4][2] = Au[2]*Au[1]*(c3+uu[2])*c1/k2;
inv_J[4][3] = Au[1]*c1*c3/k2;
inv_J[4][4] = -0.5*Au[1]*(c1*Au[2]+Au[0]*c3)/k2;
inv_J[4][5] = 0.5*Au[2]*Au[1]*c1/k2;
inv_J[5][0] = -Au[0]*Au[2]*(c1-uu[0])*c2/k3;
inv_J[5][1] = Au[2]*Au[1]*(c2+uu[1])*c1/k3;
inv_J[5][2] = Au[2]*(Au[2]*c1*c2-c1*uu[2]*Au[1]-c2*uu[2]*Au[0])/k3;
inv_J[5][3] = Au[2]*c1*c2/k3;
inv_J[5][4] = 0.5*Au[2]*Au[1]*c1/k3;
inv_J[5][5] = -0.5*Au[2]*(Au[1]*c1+Au[0]*c2)/k3;
// Solve the system by multiplying the Jacobian with the vector f:
// g = (inv_J)*f
for (int j=0; j<6; j++)
{
tmp[j] =0.0;
g[j] = 0.0;
}
for (int j=0; j<6; j++)
{
for (int i=0; i<6; i++)
{
tmp[j] = inv_J[j][i]*f[i];
g[j] += tmp[j];
}
}
// Update the solution: x_new = x_old - dx
uu[0] = uu[0] - g[0];
uu[1] = uu[1] - g[1];
uu[2] = uu[2] - g[2];
Au[0] = Au[0] - g[3];
Au[1] = Au[1] - g[4];
Au[2] = Au[2] - g[5];
// Check if the error of the solution is smaller than Tol
if ((g[0]*g[0] + g[1]*g[1] + g[2]*g[2] + g[3]*g[3]+ g[4]*g[4] + g[5]*g[5]) < Tol)
{
proceed = 0;
}
// Check if solver converges
if (iter >= MAX_ITER)
{
ASSERTL0(false,"Riemann solver for Merging Flow did not converge");
}
}
}
void Nektar::PulseWaveSystem::SetUpDomainInterfaces ( void  )
private

Definition at line 262 of file PulseWaveSystem.cpp.

References ASSERTL0, Nektar::SpatialDomains::eDirichlet, Nektar::SpatialDomains::eNotDefined, ErrorUtil::ewarning, Nektar::iterator, m_bifurcations, m_mergingJcts, m_nDomains, m_nVariables, m_vesselJcts, m_vessels, and NEKERROR.

Referenced by v_InitObject().

{
map<int,std::vector<InterfacePointShPtr> > VidToDomain;
map<int,std::vector<InterfacePointShPtr> >::iterator iter;
// loop over domain and find out if we have any undefined
// boundary conditions representing interfaces. If so make a
// map based around vid and storing the domains that are
// part of interfaces.
for(int omega = 0; omega < m_nDomains; ++omega)
{
int vesselID = omega*m_nVariables;
for(int i = 0; i < 2; ++i)
{
if(m_vessels[vesselID]->GetBndConditions()[i]->GetBoundaryConditionType() == SpatialDomains::eNotDefined)
{
// Get Vid of interface
int vid = m_vessels[vesselID]->UpdateBndCondExpansion(i)->GetExp(0)->GetGeom()->GetVid(0);
cout<<"Shared vertex id: "<<vid<<endl;
MultiRegions::ExpListSharedPtr trace = m_vessels[vesselID]->GetTrace();
InterfacePointShPtr Ipt;
bool finish = false;
// find which elmt, the lcoal vertex and the data offset of point
for(int n = 0; n < m_vessels[vesselID]->GetExpSize(); ++n)
{
for(int p = 0; p < 2; ++p)
{
if(m_vessels[vesselID]->GetTraceMap()->GetElmtToTrace()[n][p]->as<LocalRegions::Expansion>()->GetGeom()->GetVid(0) == vid)
{
int eid = m_vessels[vesselID]->GetTraceMap()->GetElmtToTrace()[n][p]->GetElmtId();
int tid = m_vessels[vesselID]->GetTrace()->GetCoeff_Offset(eid);
Ipt = MemoryManager<InterfacePoint>::AllocateSharedPtr(vid,omega,n,p,tid,i);
cout<<"Global Vid of interface point: "<<vid<<endl;
cout<<"Domain interface point belongs to: "<<omega<<endl;
cout<<"Element id of vertex: "<<n<<endl;
cout<<"Vertex id within local element: "<<p<<endl;
cout<<"Element id within the trace: "<<tid<<endl;
cout<<"Position of boundary condition in region: "<<i<<endl;
finish = true;
break;
}
}
if(finish == true)
{
break;
}
}
VidToDomain[vid].push_back(Ipt);
// finally reset boundary condition to Dirichlet
m_vessels[vesselID]->GetBndConditions()[i]
->SetBoundaryConditionType(SpatialDomains::eDirichlet);
m_vessels[vesselID+1]->GetBndConditions()[i]
->SetBoundaryConditionType(SpatialDomains::eDirichlet);
}
}
}
// loop over map and set up Interface information;
for(iter = VidToDomain.begin(); iter != VidToDomain.end(); ++iter)
{
if(iter->second.size() == 2) // Vessel jump interface
{
m_vesselJcts.push_back(iter->second);
}
else if(iter->second.size() == 3) // Bifurcation or Merging junction.
{
int nbeg = 0;
int nend = 0;
// Determine if bifurcation or merging junction
// through number of elemnt vertices that meet at
// junction. Only one vertex using a m_elmtVert=1
// indicates a bifurcation
for(int i = 0; i < 3; ++i)
{
if(iter->second[i]->m_elmtVert == 0)
{
nbeg += 1;
}
else
{
nend += 1;
}
}
// Set up Bifurcation information
if(nbeg == 2)
{
// ensure first InterfacePoint is parent
if(iter->second[0]->m_elmtVert == 1) //m_elmtVert: Vertex id in local element
{
m_bifurcations.push_back(iter->second);
}
else
{
//order points according to Riemann solver convention
InterfacePointShPtr I;
//find merging vessel
if(iter->second[1]->m_elmtVert == 1)
{
I = iter->second[0];
iter->second[0] = iter->second[1];
iter->second[1] = I;
}
else if (iter->second[2]->m_elmtVert == 1)
{
I = iter->second[0];
iter->second[0] = iter->second[2];
iter->second[2] = I;
}
NEKERROR(ErrorUtil::ewarning,"This routine has not been checked");
}
}
else
{
// ensure last InterfacePoint is merged vessel
if(iter->second[0]->m_elmtVert == 0)
{
m_mergingJcts.push_back(iter->second);
}
else
{
//order points according to Riemann solver convention
InterfacePointShPtr I;
//find merging vessel
if(iter->second[1]->m_elmtVert == 0)
{
I = iter->second[0];
iter->second[0] = iter->second[1];
iter->second[1] = I;
}
else if (iter->second[2]->m_elmtVert == 0)
{
I = iter->second[0];
iter->second[0] = iter->second[2];
iter->second[2] = I;
}
NEKERROR(ErrorUtil::ewarning,"This routine has not been checked");
}
}
}
else
{
ASSERTL0(false,"Unknown junction type");
}
}
}
Array<OneD, MultiRegions::ExpListSharedPtr> Nektar::PulseWaveSystem::UpdateVessels ( void  )
inline

Definition at line 97 of file PulseWaveSystem.h.

{
return m_vessels;
}
void Nektar::PulseWaveSystem::v_DoInitialise ( void  )
protectedvirtual

Sets up initial conditions.

Initialisation routine for multiple subdomain case. Sets the initial conditions for all arterial subdomains read from the inputfile. Sets the material properties and the A_0 area for all subdomains and fills the domain-linking boundary conditions with the initial values of their domain.

Reimplemented from Nektar::SolverUtils::UnsteadySystem.

Definition at line 427 of file PulseWaveSystem.cpp.

References Nektar::SolverUtils::EquationSystem::m_fields, m_nDomains, m_nVariables, Nektar::SolverUtils::EquationSystem::m_session, m_vessels, and Nektar::SolverUtils::EquationSystem::SetInitialConditions().

{
if (m_session->GetComm()->GetRank() == 0)
{
cout << "Initial Conditions:" << endl;
}
/* Loop over all subdomains to initialize all with the Initial
* Conditions read from the inputfile*/
for (int omega = 0; omega < m_nDomains; omega++)
{
m_fields[0] = m_vessels[m_nVariables*omega];
m_fields[1] = m_vessels[m_nVariables*omega+1];
if (m_session->GetComm()->GetRank() == 0)
{
cout << "Subdomain = " <<omega<<endl;
}
SetInitialConditions(0.0,0,omega);
}
// Reset to first definition
m_fields[0] = m_vessels[0];
m_fields[1] = m_vessels[1];
}
void Nektar::PulseWaveSystem::v_DoSolve ( void  )
protectedvirtual

Solves an unsteady problem.

NEEDS Updating:

DoSolve routine for PulseWavePropagation with multiple subdomains taken from UnsteadySystem and modified for multidomain case. Initialises the time integration scheme (as specified in the session file), and perform the time integration. Within the timestepping loop the following is done: 1. Link all arterial segments according to the network structure, solve the Riemann problem between different arterial segments and assign the values to the boundary conditions (LinkSubdomains) 2. Every arterial segment is solved independentl for this timestep. This is done by handing the solution vector 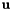$ \mathbf{u} $ and the right hand side m_ode, which is the PulseWavePropagation class in this example over to the time integration scheme

Reimplemented from Nektar::SolverUtils::UnsteadySystem.

Definition at line 472 of file PulseWaveSystem.cpp.

References CheckPoint_Output(), Nektar::SolverUtils::EquationSystem::m_checksteps, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::UnsteadySystem::m_infosteps, Nektar::SolverUtils::UnsteadySystem::m_intScheme, Nektar::SolverUtils::UnsteadySystem::m_intSoln, m_nDomains, m_nVariables, Nektar::SolverUtils::UnsteadySystem::m_ode, Nektar::SolverUtils::EquationSystem::m_session, Nektar::SolverUtils::EquationSystem::m_steps, Nektar::SolverUtils::EquationSystem::m_time, Nektar::SolverUtils::EquationSystem::m_timestep, m_vessels, Nektar::Timer::Start(), Nektar::Timer::Stop(), Nektar::Timer::TimePerTest(), and Vmath::Vcopy().

{
NekDouble IntegrationTime = 0.0;
int i,n,nchk = 1;
Array<OneD, Array<OneD,NekDouble> > fields(m_nVariables);
for(int i = 0; i < m_nVariables; ++i)
{
fields[i] = m_vessels[i]->UpdatePhys();
m_fields[i]->SetPhysState(false);
}
m_intSoln = m_intScheme->InitializeScheme(
m_timestep,fields,m_time,m_ode);
// Time loop
for(n = 0; n < m_steps; ++n)
{
Timer timer;
timer.Start();
fields = m_intScheme->TimeIntegrate(n,m_timestep,m_intSoln,m_ode);
//cout<<"integration: "<<fields[0][fields[0].num_elements()-1]<<endl;
m_time += m_timestep;
timer.Stop();
IntegrationTime += timer.TimePerTest(1);
// Write out status information.
if(m_session->GetComm()->GetRank() == 0 && !((n+1)%m_infosteps))
{
cout << "Steps: " << n+1
<< "\t Time: " << m_time
<< "\t Time-step: " << m_timestep << "\t" << endl;
}
// Transform data if needed
if(!((n+1)%m_checksteps))
{
for (i = 0; i < m_nVariables; ++i)
{
int cnt = 0;
for (int omega = 0; omega < m_nDomains; omega++)
{
m_vessels[omega*m_nVariables+i]->FwdTrans(fields[i]+cnt,
m_vessels[omega*m_nVariables+i]->UpdateCoeffs());
cnt += m_vessels[omega*m_nVariables+i]->GetTotPoints();
}
}
CheckPoint_Output(nchk++);
}
}//end of timeintegration
//Copy Array To Vessel Phys Fields
for(int i = 0; i < m_nVariables; ++i)
{
Vmath::Vcopy(fields[i].num_elements(), fields[i],1,m_vessels[i]->UpdatePhys(),1);
}
cout <<"Time-integration timing : "
<< IntegrationTime << " s" << endl << endl;
}
void Nektar::PulseWaveSystem::v_InitObject ( )
protectedvirtual

Initialisation routine for multidomain solver. Sets up the expansions for every arterial segment (m_vessels) and for one complete field m_outfield which is needed to write the postprocessing output. Also determines which upwind strategy is used (currently only upwinding scheme available) and reads blodd flow specific parameters from the inputfile 

Gets the Material Properties of each arterial segment
specified in the inputfile from section MaterialProperties

Also gets the Area at static equilibrium A_0 specified in the inputfile.

Having found these points also extract the values at the trace points and the normal direction consistent with the left adjacent definition of Fwd and Bwd

Reimplemented from Nektar::SolverUtils::UnsteadySystem.

Reimplemented in Nektar::PulseWavePropagation, and Nektar::PulseWaveSystemOutput.

Definition at line 85 of file PulseWaveSystem.cpp.

References ASSERTL0, Nektar::MultiRegions::eDiscontinuous, Nektar::SolverUtils::EquationSystem::EvaluateFunction(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), m_A_0, m_A_0_trace, m_beta, m_beta_trace, Nektar::SolverUtils::EquationSystem::m_checksteps, m_fieldPhysOffset, Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_fintime, Nektar::SolverUtils::EquationSystem::m_graph, Nektar::SolverUtils::UnsteadySystem::m_infosteps, m_nDomains, Nektar::SolverUtils::EquationSystem::m_NumQuadPointsError, m_nVariables, m_pext, Nektar::SolverUtils::EquationSystem::m_projectionType, m_rho, Nektar::SolverUtils::EquationSystem::m_session, Nektar::SolverUtils::EquationSystem::m_steps, Nektar::SolverUtils::EquationSystem::m_time, Nektar::SolverUtils::EquationSystem::m_timestep, m_trace_fwd_normal, m_upwindTypePulse, m_vessels, SetUpDomainInterfaces(), Nektar::SIZE_UpwindTypePulse, Nektar::UpwindTypeMapPulse, and Nektar::SolverUtils::EquationSystem::ZeroPhysFields().

{
// Initialise base class
UnsteadySystem::v_InitObject();
// Read the geometry and the expansion information
m_nDomains = m_graph->GetDomain().size();
// Determine projectiontype
ASSERTL0(m_session->MatchSolverInfo("Projection","DisContinuous"),"Pulse solver only set up for Discontinuous projections");
m_projectionType = MultiRegions::eDiscontinuous;
ASSERTL0(m_graph->GetMeshDimension() == 1,"Pulse wave solver only set up for expansion dimension equal to 1");
int i;
m_nVariables = m_session->GetVariables().size();
m_fields = Array<OneD, MultiRegions::ExpListSharedPtr> (m_nVariables);
m_vessels = Array<OneD, MultiRegions::ExpListSharedPtr> (m_nVariables*m_nDomains);
const std::vector<SpatialDomains::CompositeMap> domain = m_graph->GetDomain();
SpatialDomains::BoundaryConditions Allbcs(m_session, m_graph);
// Set up domains and put geometry to be only one space dimension.
int cnt = 0;
bool SetToOneSpaceDimension = true;
if(m_session->DefinesCmdLineArgument("SetToOneSpaceDimension"))
{
std::string cmdline = m_session->GetCmdLineArgument<std::string>("SetToOneSpaceDimension");
if(boost::to_upper_copy(cmdline) == "FALSE")
{
SetToOneSpaceDimension = false;
}
}
for(i = 0 ; i < m_nDomains; ++i)
{
for(int j = 0; j < m_nVariables; ++j)
{
m_vessels[cnt++] = MemoryManager<MultiRegions::DisContField1D>
::AllocateSharedPtr(m_session, m_graph, domain[i],
Allbcs,
m_session->GetVariable(j),
SetToOneSpaceDimension);
}
}
// Reset coeff and phys space to be continuous over all domains
int totcoeffs = 0;
int totphys = 0;
m_fieldPhysOffset = Array<OneD, int>(m_nDomains+1,0);
for(i = 0; i < m_nDomains; ++i)
{
totcoeffs += m_vessels[i*m_nVariables]->GetNcoeffs();
m_fieldPhysOffset[i] = totphys;
totphys += m_vessels[i*m_nVariables]->GetTotPoints();
}
m_fieldPhysOffset[m_nDomains] = totphys;
for(int n = 0; n < m_nVariables; ++n)
{
Array<OneD, NekDouble> coeffs(totcoeffs,0.0);
Array<OneD, NekDouble> phys(totphys,0.0);
Array<OneD, NekDouble> tmpcoeffs,tmpphys;
m_vessels[n]->SetCoeffsArray(coeffs);
m_vessels[n]->SetPhysArray(phys);
int cnt = m_vessels[n]->GetNcoeffs();
int cnt1 = m_vessels[n]->GetTotPoints();
for(i = 1; i < m_nDomains; ++i)
{
m_vessels[i*m_nVariables+n]->SetCoeffsArray(tmpcoeffs = coeffs + cnt);
m_vessels[i*m_nVariables+n]->SetPhysArray (tmpphys = phys + cnt1);
cnt += m_vessels[i*m_nVariables+n]->GetNcoeffs();
cnt1 += m_vessels[i*m_nVariables+n]->GetTotPoints();
}
}
// Set Default Parameter
m_session->LoadParameter("Time", m_time, 0.0);
m_session->LoadParameter("TimeStep", m_timestep, 0.01);
m_session->LoadParameter("NumSteps", m_steps, 0);
m_session->LoadParameter("IO_CheckSteps", m_checksteps, m_steps);
m_session->LoadParameter("FinTime", m_fintime, 0);
m_session->LoadParameter("NumQuadPointsError", m_NumQuadPointsError, 0);
m_fields[0] = m_vessels[0];
m_fields[1] = m_vessels[1];
// Zero all physical fields initially.
ZeroPhysFields();
// If Discontinuous Galerkin determine upwinding method to use
for (int i = 0; i < (int)SIZE_UpwindTypePulse; ++i)
{
bool match;
m_session->MatchSolverInfo("UPWINDTYPEPULSE", UpwindTypeMapPulse[i], match, false);
if (match)
{
m_upwindTypePulse = (UpwindTypePulse) i;
break;
}
}
// Load solver- specific parameters
m_session->LoadParameter("IO_InfoSteps", m_infosteps, 0);
// Load blood density
m_session->LoadParameter("rho", m_rho, 0.5);
// Load external pressure
m_session->LoadParameter("pext", m_pext, 0.0);
int nq = 0;
/**
* Gets the Material Properties of each arterial segment
* specified in the inputfile from section MaterialProperties
* Also gets the Area at static equilibrium A_0 specified in the
* inputfile.
*
* Having found these points also extract the values at the
* trace points and the normal direction consistent with the
* left adjacent definition of Fwd and Bwd
*/
m_beta = Array<OneD, Array<OneD, NekDouble> >(m_nDomains);
m_beta_trace = Array<OneD, Array<OneD, NekDouble> >(m_nDomains);
m_A_0 = Array<OneD, Array<OneD, NekDouble> >(m_nDomains);
m_A_0_trace = Array<OneD, Array<OneD, NekDouble> >(m_nDomains);
m_trace_fwd_normal = Array<OneD, Array<OneD, NekDouble> >(m_nDomains);
for (int omega = 0; omega < m_nDomains; omega++)
{
nq = m_vessels[2*omega]->GetNpoints();
m_fields[0] = m_vessels[2*omega];
m_beta[omega] = Array<OneD, NekDouble>(nq);
EvaluateFunction("beta", m_beta[omega],"MaterialProperties",0.0,omega);
m_A_0[omega] = Array<OneD, NekDouble>(nq);
EvaluateFunction("A_0", m_A_0[omega],"A_0",0.0,omega);
int nqTrace = GetTraceTotPoints();
m_beta_trace[omega] = Array<OneD, NekDouble>(nqTrace);
m_fields[0]->ExtractTracePhys(m_beta[omega],m_beta_trace[omega]);
m_A_0_trace[omega] = Array<OneD, NekDouble>(nqTrace);
m_fields[0]->ExtractTracePhys(m_A_0[omega],m_A_0_trace[omega]);
if(SetToOneSpaceDimension)
{
m_trace_fwd_normal[omega] = Array<OneD, NekDouble>(nqTrace,0.0);
MultiRegions::ExpListSharedPtr trace = m_fields[0]->GetTrace();
int nelmt_trace = trace->GetExpSize();
Array<OneD, Array<OneD, NekDouble> > normals(nelmt_trace);
for(int i = 0 ; i < nelmt_trace; ++i)
{
normals[i] = m_trace_fwd_normal[omega]+i;
}
// need to set to 1 for consistency since boundary
// conditions may not have coordim=1
trace->GetExp(0)->GetGeom()->SetCoordim(1);
trace->GetNormals(normals);
}
}
SetUpDomainInterfaces();
}
NekDouble Nektar::PulseWaveSystem::v_L2Error ( unsigned int  field,
const Array< OneD, NekDouble > &  exactsoln = NullNekDouble1DArray,
bool  Normalised = false 
)
protectedvirtual

Compute the L2 error between fields and a given exact solution.

Reimplemented from Nektar::SolverUtils::EquationSystem.

Definition at line 1157 of file PulseWaveSystem.cpp.

References ASSERTL0, Nektar::SolverUtils::EquationSystem::EvaluateFunction(), Nektar::SolverUtils::EquationSystem::GetNpoints(), Nektar::SolverUtils::EquationSystem::m_comm, m_nDomains, Nektar::SolverUtils::EquationSystem::m_NumQuadPointsError, m_nVariables, Nektar::SolverUtils::EquationSystem::m_session, Nektar::SolverUtils::EquationSystem::m_time, m_vessels, and Nektar::LibUtilities::ReduceSum.

{
NekDouble L2error = 0.0;
NekDouble L2error_dom;
NekDouble Vol = 0.0;
if(m_NumQuadPointsError == 0)
{
for (int omega = 0; omega < m_nDomains; omega++)
{
int vesselid = field + omega*m_nVariables;
if(m_vessels[vesselid]->GetPhysState() == false)
{
m_vessels[vesselid]->BwdTrans(m_vessels[vesselid]->GetCoeffs(),
m_vessels[vesselid]->UpdatePhys());
}
if(exactsoln.num_elements())
{
L2error_dom = m_vessels[vesselid]->L2(
m_vessels[vesselid]->GetPhys(),
exactsoln);
}
else if (m_session->DefinesFunction("ExactSolution"))
{
Array<OneD, NekDouble> exactsoln(m_vessels[vesselid]->GetNpoints());
LibUtilities::EquationSharedPtr vEqu
= m_session->GetFunction("ExactSolution",field,omega);
EvaluateFunction(m_session->GetVariable(field),exactsoln,"ExactSolution",
m_time);
L2error_dom = m_vessels[vesselid]->L2(
m_vessels[vesselid]->GetPhys(),
exactsoln);
}
else
{
L2error_dom = m_vessels[vesselid]->L2(
m_vessels[vesselid]->GetPhys());
}
L2error += L2error_dom*L2error_dom;
if(Normalised == true)
{
Array<OneD, NekDouble> one(m_vessels[vesselid]->GetNpoints(), 1.0);
Vol += m_vessels[vesselid]->PhysIntegral(one);
}
}
}
else
{
ASSERTL0(false,"Not set up");
}
if(Normalised == true)
{
m_comm->AllReduce(Vol, LibUtilities::ReduceSum);
L2error = sqrt(L2error/Vol);
}
else
{
L2error = sqrt(L2error);
}
return L2error;
}
NekDouble Nektar::PulseWaveSystem::v_LinfError ( unsigned int  field,
const Array< OneD, NekDouble > &  exactsoln = NullNekDouble1DArray 
)
protectedvirtual

Compute the L_inf error between fields and a given exact solution.

Compute the error in the L_inf-norm

Parameters
fieldThe field to compare.
exactsolnThe exact solution to compare with.
Returns
Error in the L_inft-norm.

Reimplemented from Nektar::SolverUtils::EquationSystem.

Definition at line 1241 of file PulseWaveSystem.cpp.

References ASSERTL0, Nektar::SolverUtils::EquationSystem::EvaluateFunction(), Nektar::SolverUtils::EquationSystem::GetNpoints(), m_nDomains, Nektar::SolverUtils::EquationSystem::m_NumQuadPointsError, m_nVariables, Nektar::SolverUtils::EquationSystem::m_session, Nektar::SolverUtils::EquationSystem::m_time, and m_vessels.

{
NekDouble LinferrorDom, Linferror = -1.0;
for (int omega = 0; omega < m_nDomains; omega++)
{
int vesselid = field + omega*m_nVariables;
if(m_NumQuadPointsError == 0)
{
if(m_vessels[vesselid]->GetPhysState() == false)
{
m_vessels[vesselid]->BwdTrans(m_vessels[vesselid]->GetCoeffs(),
m_vessels[vesselid]->UpdatePhys());
}
if(exactsoln.num_elements())
{
LinferrorDom = m_vessels[vesselid]->Linf(
m_vessels[vesselid]->GetPhys(),
exactsoln);
}
else if (m_session->DefinesFunction("ExactSolution"))
{
Array<OneD, NekDouble> exactsoln(m_vessels[vesselid]->GetNpoints());
EvaluateFunction(m_session->GetVariable(field),exactsoln,"ExactSolution",
m_time);
LinferrorDom = m_vessels[vesselid]->Linf(
m_vessels[vesselid]->GetPhys(),
exactsoln);
}
else
{
LinferrorDom = 0.0;
}
Linferror = (Linferror > LinferrorDom)? Linferror:LinferrorDom;
}
else
{
ASSERTL0(false,"ErrorExtraPoints not allowed for this solver");
}
}
return Linferror;
}
void Nektar::PulseWaveSystem::v_Output ( void  )
protectedvirtual

Writes the .fld file at the end of the simulation. Similar to the normal v_Output however the Multidomain output has to be prepared.

Write the field data to file. The file is named according to the session name with the extension .fld appended.

Reimplemented from Nektar::SolverUtils::EquationSystem.

Definition at line 1082 of file PulseWaveSystem.cpp.

References Nektar::SolverUtils::EquationSystem::m_sessionName, and WriteVessels().

{
/**
* Write the field data to file. The file is named according to the session
* name with the extension .fld appended.
*/
std::string outname = m_sessionName + ".fld";
WriteVessels(outname);
}
void Nektar::PulseWaveSystem::WriteVessels ( const std::string &  outname)
protected

Write input fields to the given filename.

Writes the field data to a file with the given filename.

Parameters
outnameFilename to write to.

Definition at line 1111 of file PulseWaveSystem.cpp.

References Nektar::SolverUtils::EquationSystem::m_fieldMetaDataMap, m_nDomains, m_nVariables, Nektar::SolverUtils::EquationSystem::m_session, Nektar::SolverUtils::EquationSystem::m_time, m_vessels, and Nektar::LibUtilities::Write().

Referenced by CheckPoint_Output(), and v_Output().

{
std::vector<LibUtilities::FieldDefinitionsSharedPtr> FieldDef;
std::vector<std::string> variables = m_session->GetVariables();
for(int n = 0; n < m_nDomains; ++n)
{
m_vessels[n*m_nVariables]->GetFieldDefinitions(FieldDef);
}
std::vector<std::vector<NekDouble> > FieldData(FieldDef.size());
int nFieldDefPerDomain = FieldDef.size()/m_nDomains;
int cnt;
// Copy Data into FieldData and set variable
for(int n = 0; n < m_nDomains; ++n)
{
for(int j = 0; j < m_nVariables; ++j)
{
for(int i = 0; i < nFieldDefPerDomain; ++i)
{
cnt = n*nFieldDefPerDomain+i;
FieldDef[cnt]->m_fields.push_back(variables[j]);
m_vessels[n*m_nVariables]->AppendFieldData(FieldDef[cnt], FieldData[cnt], m_vessels[n*m_nVariables+j]->UpdateCoeffs());
}
}
}
// Update time in field info if required
if(m_fieldMetaDataMap.find("Time") != m_fieldMetaDataMap.end())
{
m_fieldMetaDataMap["Time"] = boost::lexical_cast<std::string>(m_time);
}
//LibUtilities::CombineFields(FieldDef, FieldData);
LibUtilities::Write(outname, FieldDef, FieldData, m_fieldMetaDataMap);
}

Member Data Documentation

Array<OneD, Array<OneD, NekDouble> > Nektar::PulseWaveSystem::m_A_0
protected

Definition at line 119 of file PulseWaveSystem.h.

Referenced by Nektar::PulseWavePropagation::SetPulseWaveBoundaryConditions(), Nektar::PulseWavePropagation::v_GetFluxVector(), and v_InitObject().

Array<OneD, Array<OneD, NekDouble> > Nektar::PulseWaveSystem::m_A_0_trace
protected

Definition at line 120 of file PulseWaveSystem.h.

Referenced by FillDataFromInterfacePoint(), v_InitObject(), and Nektar::PulseWavePropagation::v_NumericalFlux().

Array<OneD, Array<OneD, NekDouble> > Nektar::PulseWaveSystem::m_beta
protected

Definition at line 121 of file PulseWaveSystem.h.

Referenced by CalcCharacteristicVariables(), Nektar::PulseWavePropagation::SetPulseWaveBoundaryConditions(), Nektar::PulseWavePropagation::v_GetFluxVector(), and v_InitObject().

Array<OneD, Array<OneD, NekDouble> > Nektar::PulseWaveSystem::m_beta_trace
protected

Definition at line 122 of file PulseWaveSystem.h.

Referenced by FillDataFromInterfacePoint(), v_InitObject(), and Nektar::PulseWavePropagation::v_NumericalFlux().

std::vector<std::vector<InterfacePointShPtr> > Nektar::PulseWaveSystem::m_bifurcations
protected

Definition at line 127 of file PulseWaveSystem.h.

Referenced by EnforceInterfaceConditions(), and SetUpDomainInterfaces().

NekDouble Nektar::PulseWaveSystem::m_C
protected

Definition at line 115 of file PulseWaveSystem.h.

int Nektar::PulseWaveSystem::m_currentDomain
protected

Definition at line 107 of file PulseWaveSystem.h.

Referenced by Nektar::PulseWavePropagation::DoOdeRhs(), Nektar::PulseWavePropagation::v_GetFluxVector(), and Nektar::PulseWavePropagation::v_NumericalFlux().

Array<OneD, int> Nektar::PulseWaveSystem::m_fieldPhysOffset
protected

Definition at line 111 of file PulseWaveSystem.h.

Referenced by FillDataFromInterfacePoint(), and v_InitObject().

std::vector<std::vector<InterfacePointShPtr> > Nektar::PulseWaveSystem::m_mergingJcts
protected

Definition at line 128 of file PulseWaveSystem.h.

Referenced by EnforceInterfaceConditions(), and SetUpDomainInterfaces().

int Nektar::PulseWaveSystem::m_nDomains
protected

Definition at line 106 of file PulseWaveSystem.h.

Referenced by Nektar::PulseWavePropagation::DoOdeRhs(), Nektar::PulseWavePropagation::SetPulseWaveBoundaryConditions(), SetUpDomainInterfaces(), v_DoInitialise(), v_DoSolve(), v_InitObject(), v_L2Error(), v_LinfError(), and WriteVessels().

int Nektar::PulseWaveSystem::m_nVariables
protected

Definition at line 108 of file PulseWaveSystem.h.

Referenced by Nektar::PulseWavePropagation::DoOdeProjection(), Nektar::PulseWavePropagation::DoOdeRhs(), EnforceInterfaceConditions(), FillDataFromInterfacePoint(), SetUpDomainInterfaces(), v_DoInitialise(), v_DoSolve(), Nektar::PulseWavePropagation::v_GetFluxVector(), v_InitObject(), v_L2Error(), v_LinfError(), Nektar::PulseWavePropagation::v_NumericalFlux(), and WriteVessels().

NekDouble Nektar::PulseWaveSystem::m_pext
protected

Definition at line 113 of file PulseWaveSystem.h.

Referenced by Nektar::PulseWavePropagation::RiemannSolverUpwind(), Nektar::PulseWavePropagation::v_GetFluxVector(), and v_InitObject().

NekDouble Nektar::PulseWaveSystem::m_pout
protected

Definition at line 117 of file PulseWaveSystem.h.

NekDouble Nektar::PulseWaveSystem::m_rho
protected

Definition at line 112 of file PulseWaveSystem.h.

Referenced by BifurcationRiemann(), CalcCharacteristicVariables(), JunctionRiemann(), MergingRiemann(), Nektar::PulseWavePropagation::RiemannSolverUpwind(), Nektar::PulseWavePropagation::v_GetFluxVector(), and v_InitObject().

NekDouble Nektar::PulseWaveSystem::m_RT
protected

Definition at line 116 of file PulseWaveSystem.h.

Array<OneD, Array<OneD, NekDouble> > Nektar::PulseWaveSystem::m_trace_fwd_normal
protected

Definition at line 123 of file PulseWaveSystem.h.

Referenced by v_InitObject(), and Nektar::PulseWavePropagation::v_NumericalFlux().

UpwindTypePulse Nektar::PulseWaveSystem::m_upwindTypePulse
protected

Definition at line 109 of file PulseWaveSystem.h.

Referenced by v_InitObject(), and Nektar::PulseWavePropagation::v_NumericalFlux().

std::vector<std::vector<InterfacePointShPtr> > Nektar::PulseWaveSystem::m_vesselJcts
protected

Definition at line 126 of file PulseWaveSystem.h.

Referenced by EnforceInterfaceConditions(), and SetUpDomainInterfaces().

Array<OneD, MultiRegions::ExpListSharedPtr> Nektar::PulseWaveSystem::m_vessels
protected

Definition at line 105 of file PulseWaveSystem.h.

Referenced by CalcCharacteristicVariables(), Nektar::PulseWavePropagation::DoOdeRhs(), EnforceInterfaceConditions(), FillDataFromInterfacePoint(), Nektar::PulseWavePropagation::SetPulseWaveBoundaryConditions(), SetUpDomainInterfaces(), v_DoInitialise(), v_DoSolve(), Nektar::PulseWavePropagation::v_GetFluxVector(), Nektar::PulseWavePropagation::v_InitObject(), v_InitObject(), v_L2Error(), v_LinfError(), Nektar::PulseWavePropagation::v_NumericalFlux(), and WriteVessels().

Generated on Wed Mar 4 2015 16:33:34 for Nektar++ by   doxygen 1.8.1.2