Nektar++
Public Member Functions | Protected Member Functions | Private Member Functions | Private Attributes | List of all members
Nektar::LocalRegions::TetExp Class Reference

#include <TetExp.h>

Inheritance diagram for Nektar::LocalRegions::TetExp:
Inheritance graph
[legend]
Collaboration diagram for Nektar::LocalRegions::TetExp:
Collaboration graph
[legend]

Public Member Functions

 TetExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc, const SpatialDomains::TetGeomSharedPtr &geom)
 Constructor using BasisKey class for quadrature points and order definition. More...
 
 TetExp (const TetExp &T)
 Copy Constructor. More...
 
 ~TetExp ()
 Destructor. More...
 
- Public Member Functions inherited from Nektar::StdRegions::StdTetExp
 StdTetExp ()
 
 StdTetExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc)
 
 StdTetExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc, NekDouble *coeffs, NekDouble *phys)
 
 StdTetExp (const StdTetExp &T)
 
 ~StdTetExp ()
 
LibUtilities::ShapeType DetShapeType () const
 
NekDouble PhysEvaluate3D (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
 Single Point Evaluation. More...
 
- Public Member Functions inherited from Nektar::StdRegions::StdExpansion3D
 StdExpansion3D ()
 
 StdExpansion3D (int numcoeffs, const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc)
 
 StdExpansion3D (const StdExpansion3D &T)
 
virtual ~StdExpansion3D ()
 
void PhysTensorDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray_d1, Array< OneD, NekDouble > &outarray_d2, Array< OneD, NekDouble > &outarray_d3)
 Calculate the 3D derivative in the local tensor/collapsed coordinate at the physical points. More...
 
void BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)
 
void IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)
 
- Public Member Functions inherited from Nektar::StdRegions::StdExpansion
 StdExpansion ()
 Default Constructor. More...
 
 StdExpansion (const int numcoeffs, const int numbases, const LibUtilities::BasisKey &Ba=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bb=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bc=LibUtilities::NullBasisKey)
 Constructor. More...
 
 StdExpansion (const StdExpansion &T)
 Copy Constructor. More...
 
virtual ~StdExpansion ()
 Destructor. More...
 
int GetNumBases () const
 This function returns the number of 1D bases used in the expansion. More...
 
const Array< OneD, const LibUtilities::BasisSharedPtr > & GetBase () const
 This function gets the shared point to basis. More...
 
const LibUtilities::BasisSharedPtr & GetBasis (int dir) const
 This function gets the shared point to basis in the dir direction. More...
 
int GetNcoeffs (void) const
 This function returns the total number of coefficients used in the expansion. More...
 
int GetTotPoints () const
 This function returns the total number of quadrature points used in the element. More...
 
LibUtilities::BasisType GetBasisType (const int dir) const
 This function returns the type of basis used in the dir direction. More...
 
int GetBasisNumModes (const int dir) const
 This function returns the number of expansion modes in the dir direction. More...
 
int EvalBasisNumModesMax (void) const
 This function returns the maximum number of expansion modes over all local directions. More...
 
LibUtilities::PointsType GetPointsType (const int dir) const
 This function returns the type of quadrature points used in the dir direction. More...
 
int GetNumPoints (const int dir) const
 This function returns the number of quadrature points in the dir direction. More...
 
const Array< OneD, const NekDouble > & GetPoints (const int dir) const
 This function returns a pointer to the array containing the quadrature points in dir direction. More...
 
int GetNverts () const
 This function returns the number of vertices of the expansion domain. More...
 
int GetNedges () const
 This function returns the number of edges of the expansion domain. More...
 
int GetEdgeNcoeffs (const int i) const
 This function returns the number of expansion coefficients belonging to the i-th edge. More...
 
int GetTotalEdgeIntNcoeffs () const
 
int GetEdgeNumPoints (const int i) const
 This function returns the number of quadrature points belonging to the i-th edge. More...
 
int DetCartesianDirOfEdge (const int edge)
 
const LibUtilities::BasisKey DetEdgeBasisKey (const int i) const
 
const LibUtilities::BasisKey DetFaceBasisKey (const int i, const int k) const
 
int GetFaceNumPoints (const int i) const
 This function returns the number of quadrature points belonging to the i-th face. More...
 
int GetFaceNcoeffs (const int i) const
 This function returns the number of expansion coefficients belonging to the i-th face. More...
 
int GetFaceIntNcoeffs (const int i) const
 
int GetTotalFaceIntNcoeffs () const
 
LibUtilities::PointsKey GetFacePointsKey (const int i, const int j) const
 
int NumBndryCoeffs (void) const
 
int NumDGBndryCoeffs (void) const
 
LibUtilities::BasisType GetEdgeBasisType (const int i) const
 This function returns the type of expansion basis on the i-th edge. More...
 
const LibUtilities::PointsKey GetNodalPointsKey () const
 This function returns the type of expansion Nodal point type if defined. More...
 
int GetNfaces () const
 This function returns the number of faces of the expansion domain. More...
 
int GetNtrace () const
 Returns the number of trace elements connected to this element. More...
 
LibUtilities::ShapeType DetShapeType () const
 This function returns the shape of the expansion domain. More...
 
boost::shared_ptr< StdExpansion > GetStdExp (void) const
 
int GetShapeDimension () const
 
bool IsBoundaryInteriorExpansion ()
 
bool IsNodalNonTensorialExp ()
 
void BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 This function performs the Backward transformation from coefficient space to physical space. More...
 
void FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 This function performs the Forward transformation from physical space to coefficient space. More...
 
void FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
NekDouble Integral (const Array< OneD, const NekDouble > &inarray)
 This function integrates the specified function over the domain. More...
 
void FillMode (const int mode, Array< OneD, NekDouble > &outarray)
 This function fills the array outarray with the mode-th mode of the expansion. More...
 
void IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 this function calculates the inner product of a given function f with the different modes of the expansion More...
 
void IProductWRTBase (const Array< OneD, const NekDouble > &base, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, int coll_check)
 
void IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
int GetElmtId ()
 Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...
 
void SetElmtId (const int id)
 Set the element id of this expansion when used in a list by returning value of m_elmt_id. More...
 
void GetCoords (Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2=NullNekDouble1DArray, Array< OneD, NekDouble > &coords_3=NullNekDouble1DArray)
 this function returns the physical coordinates of the quadrature points of the expansion More...
 
void GetCoord (const Array< OneD, const NekDouble > &Lcoord, Array< OneD, NekDouble > &coord)
 given the coordinates of a point of the element in the local collapsed coordinate system, this function calculates the physical coordinates of the point More...
 
DNekMatSharedPtr GetStdMatrix (const StdMatrixKey &mkey)
 
DNekBlkMatSharedPtr GetStdStaticCondMatrix (const StdMatrixKey &mkey)
 
IndexMapValuesSharedPtr GetIndexMap (const IndexMapKey &ikey)
 
const Array< OneD, const NekDouble > & GetPhysNormals (void)
 
void SetPhysNormals (Array< OneD, const NekDouble > &normal)
 
virtual void SetUpPhysNormals (const int edge)
 
void NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
void NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)
 
DNekScalBlkMatSharedPtr GetLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)
 
void DropLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)
 
StdRegions::Orientation GetForient (int face)
 
StdRegions::Orientation GetEorient (int edge)
 
StdRegions::Orientation GetPorient (int point)
 
StdRegions::Orientation GetCartesianEorient (int edge)
 
void SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)
 
void SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
int CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)
 
void ExtractDataToCoeffs (const NekDouble *data, const std::vector< unsigned int > &nummodes, const int nmodes_offset, NekDouble *coeffs)
 
NekDouble StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)
 
int GetCoordim ()
 
void GetBoundaryMap (Array< OneD, unsigned int > &outarray)
 
void GetInteriorMap (Array< OneD, unsigned int > &outarray)
 
int GetVertexMap (const int localVertexId, bool useCoeffPacking=false)
 
void GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
void GetFaceInteriorMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
void GetEdgeToElementMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
void GetFaceToElementMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int nummodesA=-1, int nummodesB=-1)
 
void GetEdgePhysVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Extract the physical values along edge edge from inarray into outarray following the local edge orientation and point distribution defined by defined in EdgeExp. More...
 
void GetEdgePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GetTracePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GetVertexPhysVals (const int vertex, const Array< OneD, const NekDouble > &inarray, NekDouble &outarray)
 
void GetEdgeInterpVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GetEdgeQFactors (const int edge, Array< OneD, NekDouble > &outarray)
 Extract the metric factors to compute the contravariant fluxes along edge edge and stores them into outarray following the local edge orientation (i.e. anticlockwise convention). More...
 
void GetFacePhysVals (const int face, const boost::shared_ptr< StdExpansion > &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient=eNoOrientation)
 
void MultiplyByQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
DNekMatSharedPtr CreateGeneralMatrix (const StdMatrixKey &mkey)
 this function generates the mass matrix $\mathbf{M}[i][j] = \int \phi_i(\mathbf{x}) \phi_j(\mathbf{x}) d\mathbf{x}$ More...
 
void GeneralMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDerivMatrixOp (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDirectionalDerivMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassLevelCurvatureMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LinearAdvectionDiffusionReactionMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)
 
void HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
DNekMatSharedPtr GenMatrix (const StdMatrixKey &mkey)
 
void PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
 
void PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void PhysDeriv_s (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_ds)
 
void PhysDeriv_n (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_dn)
 
void PhysDirectionalDeriv (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &direction, Array< OneD, NekDouble > &outarray)
 
void StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
 
void StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void AddRobinMassMatrix (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, DNekMatSharedPtr &inoutmat)
 
void AddRobinEdgeContribution (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, Array< OneD, NekDouble > &coeffs)
 
NekDouble PhysEvaluate (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
 This function evaluates the expansion at a single (arbitrary) point of the domain. More...
 
NekDouble PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)
 This function evaluates the expansion at a single (arbitrary) point of the domain. More...
 
void LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)
 Convert local cartesian coordinate xi into local collapsed coordinates eta. More...
 
const boost::shared_ptr< SpatialDomains::GeomFactors > & GetMetricInfo (void) const
 
virtual int v_GetElmtId ()
 Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...
 
virtual const Array< OneD, const NekDouble > & v_GetPhysNormals (void)
 
virtual void v_SetPhysNormals (Array< OneD, const NekDouble > &normal)
 
virtual void v_SetUpPhysNormals (const int edge)
 
virtual void v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
virtual void v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)
 
virtual StdRegions::Orientation v_GetEorient (int edge)
 
virtual StdRegions::Orientation v_GetCartesianEorient (int edge)
 
virtual StdRegions::Orientation v_GetPorient (int point)
 
NekDouble Linf (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
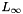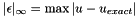 Function to evaluate the discrete $ L_\infty$ error $ |\epsilon|_\infty = \max |u - u_{exact}|$ where $ u_{exact}$ is given by the array sol. More...
 
NekDouble L2 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
 Function to evaluate the discrete 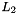$ L_2$ error, $ | \epsilon |_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 dx \right]^{1/2} d\xi_1 $ where $ u_{exact}$ is given by the array sol. More...
 
NekDouble H1 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
 Function to evaluate the discrete 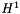$ H^1$ error, $ | \epsilon |^1_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 + \nabla(u - u_{exact})\cdot\nabla(u - u_{exact})\cdot dx \right]^{1/2} d\xi_1 $ where $ u_{exact}$ is given by the array sol. More...
 
const NormalVector & GetEdgeNormal (const int edge) const
 
void ComputeEdgeNormal (const int edge)
 
void NegateEdgeNormal (const int edge)
 
bool EdgeNormalNegated (const int edge)
 
void ComputeFaceNormal (const int face)
 
void NegateFaceNormal (const int face)
 
void ComputeVertexNormal (const int vertex)
 
const NormalVector & GetFaceNormal (const int face) const
 
const NormalVector & GetVertexNormal (const int vertex) const
 
const NormalVector & GetSurfaceNormal (const int id) const
 
const LibUtilities::PointsKeyVector GetPointsKeys () const
 
Array< OneD, unsigned int > GetEdgeInverseBoundaryMap (int eid)
 
Array< OneD, unsigned int > GetFaceInverseBoundaryMap (int fid, StdRegions::Orientation faceOrient=eNoOrientation)
 
DNekMatSharedPtr BuildInverseTransformationMatrix (const DNekScalMatSharedPtr &m_transformationmatrix)
 
void PhysInterpToSimplexEquiSpaced (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 This function performs an interpolation from the physical space points provided at input into an array of equispaced points which are not the collapsed coordinate. So for a tetrahedron you will only get a tetrahedral number of values. More...
 
void GetSimplexEquiSpacedConnectivity (Array< OneD, int > &conn, bool standard=true)
 This function provides the connectivity of local simplices (triangles or tets) to connect the equispaced data points provided by PhysInterpToSimplexEquiSpaced. More...
 
template<class T >
boost::shared_ptr< T > as ()
 
void IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)
 
- Public Member Functions inherited from Nektar::LocalRegions::Expansion3D
 Expansion3D (SpatialDomains::Geometry3DSharedPtr pGeom)
 
virtual ~Expansion3D ()
 
void SetFaceExp (const int face, Expansion2DSharedPtr &f)
 
Expansion2DSharedPtr GetFaceExp (const int face)
 
void SetTraceToGeomOrientation (Array< OneD, NekDouble > &inout)
 Align trace orientation with the geometry orientation. More...
 
void SetFaceToGeomOrientation (const int face, Array< OneD, NekDouble > &inout)
 Align face orientation with the geometry orientation. More...
 
void AddHDGHelmholtzFaceTerms (const NekDouble tau, const int edge, Array< OneD, NekDouble > &facePhys, const StdRegions::VarCoeffMap &dirForcing, Array< OneD, NekDouble > &outarray)
 
void AddNormTraceInt (const int dir, Array< OneD, ExpansionSharedPtr > &FaceExp, Array< OneD, Array< OneD, NekDouble > > &faceCoeffs, Array< OneD, NekDouble > &outarray)
 
void AddNormTraceInt (const int dir, Array< OneD, const NekDouble > &inarray, Array< OneD, ExpansionSharedPtr > &FaceExp, Array< OneD, NekDouble > &outarray, const StdRegions::VarCoeffMap &varcoeffs)
 
void AddFaceBoundaryInt (const int face, ExpansionSharedPtr &FaceExp, Array< OneD, NekDouble > &facePhys, Array< OneD, NekDouble > &outarray, const StdRegions::VarCoeffMap &varcoeffs=StdRegions::NullVarCoeffMap)
 
SpatialDomains::Geometry3DSharedPtr GetGeom3D () const
 
- Public Member Functions inherited from Nektar::LocalRegions::Expansion
 Expansion (SpatialDomains::GeometrySharedPtr pGeom)
 
 Expansion (const Expansion &pSrc)
 
virtual ~Expansion ()
 
DNekScalMatSharedPtr GetLocMatrix (const LocalRegions::MatrixKey &mkey)
 
DNekScalMatSharedPtr GetLocMatrix (const StdRegions::MatrixType mtype, const StdRegions::ConstFactorMap &factors=StdRegions::NullConstFactorMap, const StdRegions::VarCoeffMap &varcoeffs=StdRegions::NullVarCoeffMap)
 
SpatialDomains::GeometrySharedPtr GetGeom () const
 
void Reset ()
 
virtual const SpatialDomains::GeomFactorsSharedPtr & v_GetMetricInfo () const
 
DNekMatSharedPtr BuildTransformationMatrix (const DNekScalMatSharedPtr &r_bnd, const StdRegions::MatrixType matrixType)
 
DNekMatSharedPtr BuildVertexMatrix (const DNekScalMatSharedPtr &r_bnd)
 
void AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
void AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
void AddFaceNormBoundaryInt (const int face, const boost::shared_ptr< Expansion > &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
void DGDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, Array< OneD, NekDouble > > &coeffs, Array< OneD, NekDouble > &outarray)
 

Protected Member Functions

virtual NekDouble v_Integral (const Array< OneD, const NekDouble > &inarray)
 Integrate the physical point list inarray over region. More...
 
virtual void v_PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2)
 Differentiate inarray in the three coordinate directions. More...
 
virtual void v_FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Forward transform from physical quadrature space stored in inarray and evaluate the expansion coefficients and store in (this)->_coeffs. More...
 
virtual void v_IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Calculate the inner product of inarray with respect to the basis B=m_base0*m_base1*m_base2 and put into outarray: More...
 
virtual void v_IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)
 
virtual void v_IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 Calculates the inner product 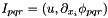$ I_{pqr} = (u, \partial_{x_i} \phi_{pqr}) $. More...
 
virtual NekDouble v_StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)
 
virtual NekDouble v_PhysEvaluate (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
 
virtual void v_GetCoord (const Array< OneD, const NekDouble > &Lcoords, Array< OneD, NekDouble > &coords)
 Get the coordinates "coords" at the local coordinates "Lcoords". More...
 
virtual void v_GetCoords (Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2, Array< OneD, NekDouble > &coords_3)
 
virtual LibUtilities::ShapeType v_DetShapeType () const
 Return Shape of region, using ShapeType enum list. More...
 
virtual StdRegions::StdExpansionSharedPtr v_GetStdExp (void) const
 
virtual int v_GetCoordim ()
 
virtual void v_ExtractDataToCoeffs (const NekDouble *data, const std::vector< unsigned int > &nummodes, const int mode_offset, NekDouble *coeffs)
 Unpack data from input file assuming it comes from the same expansion type. More...
 
virtual void v_GetFacePhysVals (const int face, const StdRegions::StdExpansionSharedPtr &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient)
 Returns the physical values at the quadrature points of a face. More...
 
virtual void v_GetTracePhysVals (const int face, const StdRegions::StdExpansionSharedPtr &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient)
 Returns the physical values at the quadrature points of a face Wrapper function to v_GetFacePhysVals. More...
 
void v_ComputeFaceNormal (const int face)
 Compute the normal of a triangular face. More...
 
virtual void v_HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdRegions::StdMatrixKey &mkey)
 
virtual DNekMatSharedPtr v_GenMatrix (const StdRegions::StdMatrixKey &mkey)
 
DNekScalMatSharedPtr CreateMatrix (const MatrixKey &mkey)
 
DNekScalBlkMatSharedPtr CreateStaticCondMatrix (const MatrixKey &mkey)
 
virtual DNekMatSharedPtr v_CreateStdMatrix (const StdRegions::StdMatrixKey &mkey)
 
virtual DNekScalMatSharedPtr v_GetLocMatrix (const MatrixKey &mkey)
 
virtual DNekScalBlkMatSharedPtr v_GetLocStaticCondMatrix (const MatrixKey &mkey)
 
void v_DropLocStaticCondMatrix (const MatrixKey &mkey)
 
void SetUpInverseTransformationMatrix (const DNekMatSharedPtr &m_transformationmatrix, DNekMatSharedPtr m_inversetransformationmatrix, DNekMatSharedPtr m_inversetransposedtransformationmatrix)
 
void v_ComputeConditionNumberOfMatrix (const DNekScalMatSharedPtr &mat)
 
virtual void v_ComputeLaplacianMetric ()
 
- Protected Member Functions inherited from Nektar::StdRegions::StdTetExp
virtual void v_PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2)
 
virtual void v_StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)
 
virtual void v_IProductWRTBase_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)
 
virtual void v_IProductWRTDerivBase_MatOp (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)
 
virtual void v_FillMode (const int mode, Array< OneD, NekDouble > &outarray)
 
virtual int v_GetNverts () const
 
virtual int v_GetNedges () const
 
virtual int v_GetNfaces () const
 
virtual int v_NumBndryCoeffs () const
 
virtual int v_NumDGBndryCoeffs () const
 
virtual int v_GetEdgeNcoeffs (const int i) const
 
virtual int v_GetTotalEdgeIntNcoeffs () const
 
virtual int v_GetFaceNcoeffs (const int i) const
 
virtual int v_GetFaceIntNcoeffs (const int i) const
 
virtual int v_GetTotalFaceIntNcoeffs () const
 
virtual int v_GetFaceNumPoints (const int i) const
 
virtual LibUtilities::PointsKey v_GetFacePointsKey (const int i, const int j) const
 
virtual int v_CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)
 
virtual const LibUtilities::BasisKey v_DetFaceBasisKey (const int i, const int k) const
 
virtual LibUtilities::BasisType v_GetEdgeBasisType (const int i) const
 
virtual bool v_IsBoundaryInteriorExpansion ()
 
virtual void v_GetFaceToElementMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int nummodesA=-1, int nummodesB=-1)
 
virtual int v_GetVertexMap (int localVertexId, bool useCoeffPacking=false)
 
virtual void v_GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
virtual void v_GetFaceInteriorMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)
 
virtual void v_GetInteriorMap (Array< OneD, unsigned int > &outarray)
 
virtual void v_GetBoundaryMap (Array< OneD, unsigned int > &outarray)
 
virtual void v_MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_GetSimplexEquiSpacedConnectivity (Array< OneD, int > &conn, bool standard=true)
 
- Protected Member Functions inherited from Nektar::StdRegions::StdExpansion3D
virtual NekDouble v_PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)
 
virtual void v_LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_NegateFaceNormal (const int face)
 
- Protected Member Functions inherited from Nektar::StdRegions::StdExpansion
DNekMatSharedPtr CreateStdMatrix (const StdMatrixKey &mkey)
 
DNekBlkMatSharedPtr CreateStdStaticCondMatrix (const StdMatrixKey &mkey)
 Create the static condensation of a matrix when using a boundary interior decomposition. More...
 
IndexMapValuesSharedPtr CreateIndexMap (const IndexMapKey &ikey)
 Create an IndexMap which contains mapping information linking any specific element shape with either its boundaries, edges, faces, verteces, etc. More...
 
void BwdTrans_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
void GeneralMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp_MatFree_Kernel (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp)
 
void LaplacianMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LaplacianMatrixOp_MatFree (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDerivMatrixOp_MatFree (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void WeakDirectionalDerivMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void MassLevelCurvatureMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void LinearAdvectionDiffusionReactionMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)
 
void HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
void HelmholtzMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)
 
virtual void v_SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)
 
- Protected Member Functions inherited from Nektar::LocalRegions::Expansion3D
virtual void v_DGDeriv (const int dir, const Array< OneD, const NekDouble > &incoeffs, Array< OneD, ExpansionSharedPtr > &FaceExp, Array< OneD, Array< OneD, NekDouble > > &faceCoeffs, Array< OneD, NekDouble > &out_d)
 Evaluate coefficients of weak deriviative in the direction dir given the input coefficicents incoeffs and the imposed boundary values in EdgeExp (which will have its phys space updated). More...
 
virtual void v_AddFaceNormBoundaryInt (const int face, const ExpansionSharedPtr &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddRobinMassMatrix (const int face, const Array< OneD, const NekDouble > &primCoeffs, DNekMatSharedPtr &inoutmat)
 
virtual StdRegions::Orientation v_GetForient (int face)
 
virtual Array< OneD, unsigned int > v_GetEdgeInverseBoundaryMap (int eid)
 
virtual Array< OneD, unsigned int > v_GetFaceInverseBoundaryMap (int fid, StdRegions::Orientation faceOrient=StdRegions::eNoOrientation)
 
virtual DNekMatSharedPtr v_BuildTransformationMatrix (const DNekScalMatSharedPtr &r_bnd, const StdRegions::MatrixType matrixType)
 
virtual DNekMatSharedPtr v_BuildInverseTransformationMatrix (const DNekScalMatSharedPtr &m_transformationmatrix)
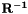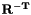 Build inverse and inverse transposed transformation matrix: $\mathbf{R^{-1}}$ and $\mathbf{R^{-T}}$. More...
 
virtual DNekMatSharedPtr v_BuildVertexMatrix (const DNekScalMatSharedPtr &r_bnd)
 
- Protected Member Functions inherited from Nektar::LocalRegions::Expansion
void ComputeLaplacianMetric ()
 
void ComputeQuadratureMetric ()
 
virtual void v_MultiplyByQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 
virtual void v_AddFaceNormBoundaryInt (const int face, const boost::shared_ptr< Expansion > &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)
 

Private Member Functions

 TetExp ()
 
void GeneralMatrixOp_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
 
virtual void v_LaplacianMatrixOp_MatFree_Kernel (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp)
 

Private Attributes

LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
 
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
 

Additional Inherited Members

- Protected Attributes inherited from Nektar::StdRegions::StdExpansion3D
std::map< int, NormalVector > m_faceNormals
 
std::map< int, bool > m_negatedNormals
 
- Protected Attributes inherited from Nektar::StdRegions::StdExpansion
Array< OneD, LibUtilities::BasisSharedPtr > m_base
 
int m_elmt_id
 
int m_ncoeffs
 
LibUtilities::NekManager< StdMatrixKey, DNekMat, StdMatrixKey::opLess > m_stdMatrixManager
 
LibUtilities::NekManager< StdMatrixKey, DNekBlkMat, StdMatrixKey::opLess > m_stdStaticCondMatrixManager
 
LibUtilities::NekManager< IndexMapKey, IndexMapValues, IndexMapKey::opLess > m_IndexMapManager
 
- Protected Attributes inherited from Nektar::LocalRegions::Expansion
SpatialDomains::GeometrySharedPtr m_geom
 
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
 
MetricMap m_metrics
 

Detailed Description

Defines a Tetrahedral local expansion.

Definition at line 51 of file TetExp.h.

Constructor & Destructor Documentation

Nektar::LocalRegions::TetExp::TetExp ( const LibUtilities::BasisKey &  Ba,
const LibUtilities::BasisKey &  Bb,
const LibUtilities::BasisKey &  Bc,
const SpatialDomains::TetGeomSharedPtr &  geom 
)

Constructor using BasisKey class for quadrature points and order definition.

Parameters
BaBasis key for first coordinate.
BbBasis key for second coordinate.
BcBasis key for third coordinate.

Definition at line 58 of file TetExp.cpp.

62  :
63  StdExpansion (LibUtilities::StdTetData::getNumberOfCoefficients(Ba.GetNumModes(),Bb.GetNumModes(),Bc.GetNumModes()),3,Ba,Bb,Bc),
64  StdExpansion3D(LibUtilities::StdTetData::getNumberOfCoefficients(Ba.GetNumModes(),Bb.GetNumModes(),Bc.GetNumModes()),Ba,Bb,Bc),
65  StdRegions::StdTetExp(Ba,Bb,Bc),
66  Expansion (geom),
67  Expansion3D (geom),
68  m_matrixManager(
69  boost::bind(&TetExp::CreateMatrix, this, _1),
70  std::string("TetExpMatrix")),
71  m_staticCondMatrixManager(
72  boost::bind(&TetExp::CreateStaticCondMatrix, this, _1),
73  std::string("TetExpStaticCondMatrix"))
74  {
75  }
Nektar::LocalRegions::TetExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: TetExp.h:218
Nektar::LibUtilities::StdTetData::getNumberOfCoefficients
int getNumberOfCoefficients(int Na, int Nb, int Nc)
Definition: ShapeType.hpp:186
Nektar::LocalRegions::TetExp::CreateStaticCondMatrix
DNekScalBlkMatSharedPtr CreateStaticCondMatrix(const MatrixKey &mkey)
Definition: TetExp.cpp:1374
Nektar::LocalRegions::TetExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: TetExp.h:219
Nektar::LocalRegions::Expansion::Expansion
Expansion(SpatialDomains::GeometrySharedPtr pGeom)
Definition: Expansion.cpp:46
Nektar::LocalRegions::TetExp::CreateMatrix
DNekScalMatSharedPtr CreateMatrix(const MatrixKey &mkey)
Definition: TetExp.cpp:1065
Nektar::StdRegions::StdExpansion::StdExpansion
StdExpansion()
Default Constructor.
Definition: StdExpansion.cpp:44
Nektar::LocalRegions::Expansion3D::Expansion3D
Expansion3D(SpatialDomains::Geometry3DSharedPtr pGeom)
Definition: Expansion3D.h:63
Nektar::LocalRegions::TetExp::TetExp ( const TetExp &  T)

Copy Constructor.

Definition at line 81 of file TetExp.cpp.

81  :
82  StdExpansion(T),
83  StdExpansion3D(T),
84  StdRegions::StdTetExp(T),
85  Expansion(T),
86  Expansion3D(T),
87  m_matrixManager(T.m_matrixManager),
88  m_staticCondMatrixManager(T.m_staticCondMatrixManager)
89  {
90  }
Nektar::LocalRegions::TetExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: TetExp.h:218
Nektar::LocalRegions::TetExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: TetExp.h:219
Nektar::LocalRegions::Expansion::Expansion
Expansion(SpatialDomains::GeometrySharedPtr pGeom)
Definition: Expansion.cpp:46
Nektar::StdRegions::StdExpansion::StdExpansion
StdExpansion()
Default Constructor.
Definition: StdExpansion.cpp:44
Nektar::LocalRegions::Expansion3D::Expansion3D
Expansion3D(SpatialDomains::Geometry3DSharedPtr pGeom)
Definition: Expansion3D.h:63
Nektar::LocalRegions::TetExp::~TetExp ( )

Destructor.

Definition at line 95 of file TetExp.cpp.

96  {
97  }
Nektar::LocalRegions::TetExp::TetExp ( )
private

Member Function Documentation

DNekScalMatSharedPtr Nektar::LocalRegions::TetExp::CreateMatrix ( const MatrixKey &  mkey)
protected

Definition at line 1065 of file TetExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), ASSERTL2, Nektar::LocalRegions::Expansion::BuildTransformationMatrix(), Nektar::LocalRegions::Expansion::BuildVertexMatrix(), Nektar::StdRegions::StdMatrixKey::ConstFactorExists(), Nektar::StdRegions::StdTetExp::DetShapeType(), Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::eFactorLambda, Nektar::StdRegions::eFactorSVVCutoffRatio, Nektar::StdRegions::eHelmholtz, Nektar::StdRegions::eHybridDGHelmBndLam, Nektar::StdRegions::eHybridDGHelmholtz, Nektar::StdRegions::eHybridDGLamToQ0, Nektar::StdRegions::eHybridDGLamToQ1, Nektar::StdRegions::eHybridDGLamToQ2, Nektar::StdRegions::eHybridDGLamToU, Nektar::StdRegions::eInvHybridDGHelmholtz, Nektar::StdRegions::eInvLaplacianWithUnityMean, Nektar::StdRegions::eInvMass, Nektar::StdRegions::eIProductWRTBase, Nektar::StdRegions::eLaplacian, Nektar::StdRegions::eLaplacian00, Nektar::StdRegions::eLaplacian01, Nektar::StdRegions::eLaplacian02, Nektar::StdRegions::eLaplacian11, Nektar::StdRegions::eLaplacian12, Nektar::StdRegions::eLaplacian22, Nektar::StdRegions::eMass, Nektar::SpatialDomains::eNoGeomType, Nektar::StdRegions::ePreconLinearSpace, Nektar::StdRegions::ePreconLinearSpaceMass, Nektar::StdRegions::ePreconR, Nektar::StdRegions::ePreconRMass, Nektar::StdRegions::ePreconRT, Nektar::StdRegions::ePreconRTMass, Nektar::StdRegions::eWeakDeriv0, Nektar::StdRegions::eWeakDeriv1, Nektar::StdRegions::eWeakDeriv2, Nektar::StdRegions::StdExpansion::GenMatrix(), Nektar::StdRegions::StdMatrixKey::GetConstFactor(), Nektar::StdRegions::StdMatrixKey::GetConstFactors(), Nektar::StdRegions::StdExpansion::GetLocStaticCondMatrix(), Nektar::StdRegions::StdMatrixKey::GetMatrixType(), Nektar::StdRegions::StdMatrixKey::GetNVarCoeff(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdMatrixKey::GetShapeType(), Nektar::StdRegions::StdExpansion::GetStdMatrix(), Nektar::StdRegions::StdMatrixKey::GetVarCoeffs(), m_matrixManager, Nektar::LocalRegions::Expansion::m_metricinfo, and Nektar::Transpose().

1066  {
1067  DNekScalMatSharedPtr returnval;
1068  LibUtilities::PointsKeyVector ptsKeys = GetPointsKeys();
1069 
1070  ASSERTL2(m_metricinfo->GetGtype() != SpatialDomains::eNoGeomType,"Geometric information is not set up");
1071 
1072  switch(mkey.GetMatrixType())
1073  {
1074  case StdRegions::eMass:
1075  {
1076  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
1077  mkey.GetNVarCoeff())
1078  {
1079  NekDouble one = 1.0;
1080  DNekMatSharedPtr mat = GenMatrix(mkey);
1081  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
1082  }
1083  else
1084  {
1085  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1086  DNekMatSharedPtr mat = GetStdMatrix(mkey);
1087  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(jac,mat);
1088  }
1089  }
1090  break;
1091  case StdRegions::eInvMass:
1092  {
1093  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1094  {
1095  NekDouble one = 1.0;
1096  StdRegions::StdMatrixKey masskey(StdRegions::eMass,DetShapeType(),
1097  *this);
1098  DNekMatSharedPtr mat = GenMatrix(masskey);
1099  mat->Invert();
1100  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
1101  }
1102  else
1103  {
1104  NekDouble fac = 1.0/(m_metricinfo->GetJac(ptsKeys))[0];
1105  DNekMatSharedPtr mat = GetStdMatrix(mkey);
1106  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(fac,mat);
1107  }
1108  }
1109  break;
1110  case StdRegions::eWeakDeriv0:
1111  case StdRegions::eWeakDeriv1:
1112  case StdRegions::eWeakDeriv2:
1113  {
1114  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
1115  mkey.GetNVarCoeff())
1116  {
1117  NekDouble one = 1.0;
1118  DNekMatSharedPtr mat = GenMatrix(mkey);
1119 
1120  returnval = MemoryManager<DNekScalMat>
1121  ::AllocateSharedPtr(one,mat);
1122  }
1123  else
1124  {
1125  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1126  Array<TwoD, const NekDouble> df
1127  = m_metricinfo->GetDerivFactors(ptsKeys);
1128  int dir = 0;
1129 
1130  switch(mkey.GetMatrixType())
1131  {
1132  case StdRegions::eWeakDeriv0:
1133  dir = 0;
1134  break;
1135  case StdRegions::eWeakDeriv1:
1136  dir = 1;
1137  break;
1138  case StdRegions::eWeakDeriv2:
1139  dir = 2;
1140  break;
1141  default:
1142  break;
1143  }
1144 
1145  MatrixKey deriv0key(StdRegions::eWeakDeriv0,
1146  mkey.GetShapeType(), *this);
1147  MatrixKey deriv1key(StdRegions::eWeakDeriv1,
1148  mkey.GetShapeType(), *this);
1149  MatrixKey deriv2key(StdRegions::eWeakDeriv2,
1150  mkey.GetShapeType(), *this);
1151 
1152  DNekMat &deriv0 = *GetStdMatrix(deriv0key);
1153  DNekMat &deriv1 = *GetStdMatrix(deriv1key);
1154  DNekMat &deriv2 = *GetStdMatrix(deriv2key);
1155 
1156  int rows = deriv0.GetRows();
1157  int cols = deriv1.GetColumns();
1158 
1159  DNekMatSharedPtr WeakDeriv = MemoryManager<DNekMat>
1160  ::AllocateSharedPtr(rows,cols);
1161  (*WeakDeriv) = df[3*dir][0]*deriv0
1162  + df[3*dir+1][0]*deriv1
1163  + df[3*dir+2][0]*deriv2;
1164 
1165  returnval = MemoryManager<DNekScalMat>
1166  ::AllocateSharedPtr(jac,WeakDeriv);
1167  }
1168  }
1169  break;
1170  case StdRegions::eLaplacian:
1171  {
1172  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
1173  (mkey.GetNVarCoeff() > 0)||(mkey.ConstFactorExists(StdRegions::eFactorSVVCutoffRatio)))
1174  {
1175  NekDouble one = 1.0;
1176  DNekMatSharedPtr mat = GenMatrix(mkey);
1177 
1178  returnval = MemoryManager<DNekScalMat>
1179  ::AllocateSharedPtr(one,mat);
1180  }
1181  else
1182  {
1183  MatrixKey lap00key(StdRegions::eLaplacian00,
1184  mkey.GetShapeType(), *this);
1185  MatrixKey lap01key(StdRegions::eLaplacian01,
1186  mkey.GetShapeType(), *this);
1187  MatrixKey lap02key(StdRegions::eLaplacian02,
1188  mkey.GetShapeType(), *this);
1189  MatrixKey lap11key(StdRegions::eLaplacian11,
1190  mkey.GetShapeType(), *this);
1191  MatrixKey lap12key(StdRegions::eLaplacian12,
1192  mkey.GetShapeType(), *this);
1193  MatrixKey lap22key(StdRegions::eLaplacian22,
1194  mkey.GetShapeType(), *this);
1195 
1196  DNekMat &lap00 = *GetStdMatrix(lap00key);
1197  DNekMat &lap01 = *GetStdMatrix(lap01key);
1198  DNekMat &lap02 = *GetStdMatrix(lap02key);
1199  DNekMat &lap11 = *GetStdMatrix(lap11key);
1200  DNekMat &lap12 = *GetStdMatrix(lap12key);
1201  DNekMat &lap22 = *GetStdMatrix(lap22key);
1202 
1203  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1204  Array<TwoD, const NekDouble> gmat
1205  = m_metricinfo->GetGmat(ptsKeys);
1206 
1207  int rows = lap00.GetRows();
1208  int cols = lap00.GetColumns();
1209 
1210  DNekMatSharedPtr lap = MemoryManager<DNekMat>
1211  ::AllocateSharedPtr(rows,cols);
1212 
1213  (*lap) = gmat[0][0]*lap00
1214  + gmat[4][0]*lap11
1215  + gmat[8][0]*lap22
1216  + gmat[3][0]*(lap01 + Transpose(lap01))
1217  + gmat[6][0]*(lap02 + Transpose(lap02))
1218  + gmat[7][0]*(lap12 + Transpose(lap12));
1219 
1220  returnval = MemoryManager<DNekScalMat>
1221  ::AllocateSharedPtr(jac,lap);
1222  }
1223  }
1224  break;
1225  case StdRegions::eHelmholtz:
1226  {
1227  NekDouble factor = mkey.GetConstFactor(StdRegions::eFactorLambda);
1228  MatrixKey masskey(StdRegions::eMass, mkey.GetShapeType(), *this);
1229  DNekScalMat &MassMat = *(this->m_matrixManager[masskey]);
1230  MatrixKey lapkey(StdRegions::eLaplacian, mkey.GetShapeType(), *this, mkey.GetConstFactors(), mkey.GetVarCoeffs());
1231  DNekScalMat &LapMat = *(this->m_matrixManager[lapkey]);
1232 
1233  int rows = LapMat.GetRows();
1234  int cols = LapMat.GetColumns();
1235 
1236  DNekMatSharedPtr helm = MemoryManager<DNekMat>::AllocateSharedPtr(rows, cols);
1237 
1238  NekDouble one = 1.0;
1239  (*helm) = LapMat + factor*MassMat;
1240 
1241  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one, helm);
1242  }
1243  break;
1244  case StdRegions::eIProductWRTBase:
1245  {
1246  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1247  {
1248  NekDouble one = 1.0;
1249  DNekMatSharedPtr mat = GenMatrix(mkey);
1250  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
1251  }
1252  else
1253  {
1254  NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
1255  DNekMatSharedPtr mat = GetStdMatrix(mkey);
1256  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(jac,mat);
1257  }
1258  }
1259  break;
1260  case StdRegions::eHybridDGHelmholtz:
1261  case StdRegions::eHybridDGLamToU:
1262  case StdRegions::eHybridDGLamToQ0:
1263  case StdRegions::eHybridDGLamToQ1:
1264  case StdRegions::eHybridDGLamToQ2:
1265  case StdRegions::eHybridDGHelmBndLam:
1266  case StdRegions::eInvLaplacianWithUnityMean:
1267  {
1268  NekDouble one = 1.0;
1269 
1270  DNekMatSharedPtr mat = GenMatrix(mkey);
1271  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
1272  }
1273  break;
1274  case StdRegions::eInvHybridDGHelmholtz:
1275  {
1276  NekDouble one = 1.0;
1277 
1278  MatrixKey hkey(StdRegions::eHybridDGHelmholtz, DetShapeType(), *this, mkey.GetConstFactors(), mkey.GetVarCoeffs());
1279  DNekMatSharedPtr mat = GenMatrix(hkey);
1280 
1281  mat->Invert();
1282  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
1283  }
1284  break;
1285  case StdRegions::ePreconLinearSpace:
1286  {
1287  NekDouble one = 1.0;
1288  MatrixKey helmkey(StdRegions::eHelmholtz, mkey.GetShapeType(), *this, mkey.GetConstFactors(), mkey.GetVarCoeffs());
1289  DNekScalBlkMatSharedPtr helmStatCond = GetLocStaticCondMatrix(helmkey);
1290  DNekScalMatSharedPtr A =helmStatCond->GetBlock(0,0);
1291  DNekMatSharedPtr R=BuildVertexMatrix(A);
1292 
1293  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
1294  }
1295  break;
1296  case StdRegions::ePreconLinearSpaceMass:
1297  {
1298  NekDouble one = 1.0;
1299  MatrixKey masskey(StdRegions::eMass, mkey.GetShapeType(), *this);
1300  DNekScalBlkMatSharedPtr massStatCond = GetLocStaticCondMatrix(masskey);
1301  DNekScalMatSharedPtr A =massStatCond->GetBlock(0,0);
1302  DNekMatSharedPtr R=BuildVertexMatrix(A);
1303 
1304  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
1305  }
1306  break;
1307  case StdRegions::ePreconR:
1308  {
1309  NekDouble one = 1.0;
1310  MatrixKey helmkey(StdRegions::eHelmholtz, mkey.GetShapeType(), *this,mkey.GetConstFactors(), mkey.GetVarCoeffs());
1311  DNekScalBlkMatSharedPtr helmStatCond = GetLocStaticCondMatrix(helmkey);
1312  DNekScalMatSharedPtr A =helmStatCond->GetBlock(0,0);
1313 
1314  DNekScalMatSharedPtr Atmp;
1315  DNekMatSharedPtr R=BuildTransformationMatrix(A,mkey.GetMatrixType());
1316 
1317  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
1318  }
1319  break;
1320  case StdRegions::ePreconRT:
1321  {
1322  NekDouble one = 1.0;
1323  MatrixKey helmkey(StdRegions::eHelmholtz, mkey.GetShapeType(), *this,mkey.GetConstFactors(), mkey.GetVarCoeffs());
1324  DNekScalBlkMatSharedPtr helmStatCond = GetLocStaticCondMatrix(helmkey);
1325  DNekScalMatSharedPtr A =helmStatCond->GetBlock(0,0);
1326 
1327  DNekScalMatSharedPtr Atmp;
1328  DNekMatSharedPtr RT=BuildTransformationMatrix(A,mkey.GetMatrixType());
1329 
1330  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,RT);
1331  }
1332  break;
1333  case StdRegions::ePreconRMass:
1334  {
1335  NekDouble one = 1.0;
1336  MatrixKey masskey(StdRegions::eMass, mkey.GetShapeType(), *this);
1337  DNekScalBlkMatSharedPtr StatCond = GetLocStaticCondMatrix(masskey);
1338  DNekScalMatSharedPtr A =StatCond->GetBlock(0,0);
1339 
1340  DNekScalMatSharedPtr Atmp;
1341  DNekMatSharedPtr R=BuildTransformationMatrix(A,mkey.GetMatrixType());
1342 
1343  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
1344  }
1345  break;
1346  case StdRegions::ePreconRTMass:
1347  {
1348  NekDouble one = 1.0;
1349  MatrixKey masskey(StdRegions::eMass, mkey.GetShapeType(), *this);
1350  DNekScalBlkMatSharedPtr massStatCond = GetLocStaticCondMatrix(masskey);
1351  DNekScalMatSharedPtr A =massStatCond->GetBlock(0,0);
1352 
1353  DNekScalMatSharedPtr Atmp;
1354  DNekMatSharedPtr RT=BuildTransformationMatrix(A,mkey.GetMatrixType());
1355 
1356  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,RT);
1357  }
1358  break;
1359  default:
1360  {
1361  //ASSERTL0(false, "Missing definition for " + (*StdRegions::MatrixTypeMap[mkey.GetMatrixType()]));
1362  NekDouble one = 1.0;
1363  DNekMatSharedPtr mat = GenMatrix(mkey);
1364 
1365  returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
1366  }
1367  break;
1368  }
1369 
1370  return returnval;
1371  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1276
Nektar::StdRegions::StdExpansion::GenMatrix
DNekMatSharedPtr GenMatrix(const StdMatrixKey &mkey)
Definition: StdExpansion.h:1009
Nektar::LibUtilities::PointsKeyVector
std::vector< PointsKey > PointsKeyVector
Definition: Points.h:220
Nektar::LocalRegions::Expansion::BuildTransformationMatrix
DNekMatSharedPtr BuildTransformationMatrix(const DNekScalMatSharedPtr &r_bnd, const StdRegions::MatrixType matrixType)
Definition: Expansion.cpp:88
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::LocalRegions::TetExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: TetExp.h:218
Nektar::LocalRegions::Expansion::BuildVertexMatrix
DNekMatSharedPtr BuildVertexMatrix(const DNekScalMatSharedPtr &r_bnd)
Definition: Expansion.cpp:96
Nektar::StdRegions::StdExpansion::GetLocStaticCondMatrix
DNekScalBlkMatSharedPtr GetLocStaticCondMatrix(const LocalRegions::MatrixKey &mkey)
Definition: StdExpansion.h:721
Nektar::DNekMatSharedPtr
boost::shared_ptr< DNekMat > DNekMatSharedPtr
Definition: NekTypeDefs.hpp:70
Nektar::StdRegions::StdExpansion::GetStdMatrix
DNekMatSharedPtr GetStdMatrix(const StdMatrixKey &mkey)
Definition: StdExpansion.h:684
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::StdRegions::StdTetExp::DetShapeType
LibUtilities::ShapeType DetShapeType() const
Definition: StdTetExp.h:70
Nektar::DNekScalBlkMatSharedPtr
boost::shared_ptr< DNekScalBlkMat > DNekScalBlkMatSharedPtr
Definition: NekTypeDefs.hpp:74
Nektar::Transpose
NekMatrix< InnerMatrixType, BlockMatrixTag > Transpose(NekMatrix< InnerMatrixType, BlockMatrixTag > &rhs)
Definition: BlockMatrix.hpp:221
Nektar::DNekMat
NekMatrix< NekDouble, StandardMatrixTag > DNekMat
Definition: NekTypeDefs.hpp:52
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:43
ASSERTL2
#define ASSERTL2(condition, msg)
Assert Level 2 – Debugging which is used FULLDEBUG compilation mode. This level assert is designed t...
Definition: ErrorUtil.hpp:213
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Nektar::DNekScalMat
NekMatrix< NekMatrix< NekDouble, StandardMatrixTag >, ScaledMatrixTag > DNekScalMat
Definition: NekMatrixFwd.hpp:72
DNekScalBlkMatSharedPtr Nektar::LocalRegions::TetExp::CreateStaticCondMatrix ( const MatrixKey &  mkey)
protected

Definition at line 1374 of file TetExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), ASSERTL2, Nektar::SpatialDomains::eDeformed, Nektar::eFULL, Nektar::StdRegions::eHelmholtz, Nektar::StdRegions::eLaplacian, Nektar::SpatialDomains::eNoGeomType, Nektar::StdRegions::StdExpansion::GetBoundaryMap(), Nektar::StdRegions::StdExpansion::GetInteriorMap(), Nektar::LocalRegions::Expansion::GetLocMatrix(), Nektar::StdRegions::StdMatrixKey::GetMatrixType(), Nektar::StdRegions::StdMatrixKey::GetNVarCoeff(), Nektar::StdRegions::StdExpansion::GetStdStaticCondMatrix(), Nektar::LocalRegions::Expansion::m_metricinfo, Nektar::StdRegions::StdExpansion::m_ncoeffs, and Nektar::StdRegions::StdExpansion::NumBndryCoeffs().

1376  {
1377  DNekScalBlkMatSharedPtr returnval;
1378 
1379  ASSERTL2(m_metricinfo->GetGtype() != SpatialDomains::eNoGeomType,"Geometric information is not set up");
1380 
1381  // set up block matrix system
1382  unsigned int nbdry = NumBndryCoeffs();
1383  unsigned int nint = (unsigned int)(m_ncoeffs - nbdry);
1384  unsigned int exp_size[] = {nbdry, nint};
1385  unsigned int nblks = 2;
1386  returnval = MemoryManager<DNekScalBlkMat>::AllocateSharedPtr(nblks, nblks, exp_size, exp_size);
1387 
1388  NekDouble factor = 1.0;
1389  MatrixStorage AMatStorage = eFULL;
1390 
1391  switch(mkey.GetMatrixType())
1392  {
1393  case StdRegions::eLaplacian:
1394  case StdRegions::eHelmholtz: // special case since Helmholtz not defined in StdRegions
1395  // use Deformed case for both regular and deformed geometries
1396  factor = 1.0;
1397  goto UseLocRegionsMatrix;
1398  break;
1399  default:
1400  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
1401  mkey.GetNVarCoeff())
1402  {
1403  factor = 1.0;
1404  goto UseLocRegionsMatrix;
1405  }
1406  else
1407  {
1408  DNekScalMatSharedPtr mat = GetLocMatrix(mkey);
1409  factor = mat->Scale();
1410  goto UseStdRegionsMatrix;
1411  }
1412  break;
1413  UseStdRegionsMatrix:
1414  {
1415  NekDouble invfactor = 1.0/factor;
1416  NekDouble one = 1.0;
1417  DNekBlkMatSharedPtr mat = GetStdStaticCondMatrix(mkey);
1418  DNekScalMatSharedPtr Atmp;
1419  DNekMatSharedPtr Asubmat;
1420 
1421  //TODO: check below
1422  returnval->SetBlock(0,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,Asubmat = mat->GetBlock(0,0)));
1423  returnval->SetBlock(0,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,Asubmat = mat->GetBlock(0,1)));
1424  returnval->SetBlock(1,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,Asubmat = mat->GetBlock(1,0)));
1425  returnval->SetBlock(1,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(invfactor,Asubmat = mat->GetBlock(1,1)));
1426  }
1427  break;
1428  UseLocRegionsMatrix:
1429  {
1430  int i,j;
1431  NekDouble invfactor = 1.0/factor;
1432  NekDouble one = 1.0;
1433  DNekScalMat &mat = *GetLocMatrix(mkey);
1434  DNekMatSharedPtr A = MemoryManager<DNekMat>::AllocateSharedPtr(nbdry,nbdry,AMatStorage);
1435  DNekMatSharedPtr B = MemoryManager<DNekMat>::AllocateSharedPtr(nbdry,nint);
1436  DNekMatSharedPtr C = MemoryManager<DNekMat>::AllocateSharedPtr(nint,nbdry);
1437  DNekMatSharedPtr D = MemoryManager<DNekMat>::AllocateSharedPtr(nint,nint);
1438 
1439  Array<OneD,unsigned int> bmap(nbdry);
1440  Array<OneD,unsigned int> imap(nint);
1441  GetBoundaryMap(bmap);
1442  GetInteriorMap(imap);
1443 
1444  for(i = 0; i < nbdry; ++i)
1445  {
1446  for(j = 0; j < nbdry; ++j)
1447  {
1448  (*A)(i,j) = mat(bmap[i],bmap[j]);
1449  }
1450 
1451  for(j = 0; j < nint; ++j)
1452  {
1453  (*B)(i,j) = mat(bmap[i],imap[j]);
1454  }
1455  }
1456 
1457  for(i = 0; i < nint; ++i)
1458  {
1459  for(j = 0; j < nbdry; ++j)
1460  {
1461  (*C)(i,j) = mat(imap[i],bmap[j]);
1462  }
1463 
1464  for(j = 0; j < nint; ++j)
1465  {
1466  (*D)(i,j) = mat(imap[i],imap[j]);
1467  }
1468  }
1469 
1470  // Calculate static condensed system
1471  if(nint)
1472  {
1473  D->Invert();
1474  (*B) = (*B)*(*D);
1475  (*A) = (*A) - (*B)*(*C);
1476  }
1477 
1478  DNekScalMatSharedPtr Atmp;
1479 
1480  returnval->SetBlock(0,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,A));
1481  returnval->SetBlock(0,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,B));
1482  returnval->SetBlock(1,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,C));
1483  returnval->SetBlock(1,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(invfactor,D));
1484 
1485  }
1486  break;
1487  }
1488  return returnval;
1489  }
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::DNekMatSharedPtr
boost::shared_ptr< DNekMat > DNekMatSharedPtr
Definition: NekTypeDefs.hpp:70
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::StdRegions::StdExpansion::GetStdStaticCondMatrix
DNekBlkMatSharedPtr GetStdStaticCondMatrix(const StdMatrixKey &mkey)
Definition: StdExpansion.h:689
Nektar::DNekScalBlkMatSharedPtr
boost::shared_ptr< DNekScalBlkMat > DNekScalBlkMatSharedPtr
Definition: NekTypeDefs.hpp:74
Nektar::StdRegions::StdExpansion::GetInteriorMap
void GetInteriorMap(Array< OneD, unsigned int > &outarray)
Definition: StdExpansion.h:795
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:43
Nektar::DNekBlkMatSharedPtr
boost::shared_ptr< DNekBlkMat > DNekBlkMatSharedPtr
Definition: NekTypeDefs.hpp:72
Nektar::LocalRegions::Expansion::GetLocMatrix
DNekScalMatSharedPtr GetLocMatrix(const LocalRegions::MatrixKey &mkey)
Definition: Expansion.cpp:83
ASSERTL2
#define ASSERTL2(condition, msg)
Assert Level 2 – Debugging which is used FULLDEBUG compilation mode. This level assert is designed t...
Definition: ErrorUtil.hpp:213
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Nektar::DNekScalMat
NekMatrix< NekMatrix< NekDouble, StandardMatrixTag >, ScaledMatrixTag > DNekScalMat
Definition: NekMatrixFwd.hpp:72
Nektar::StdRegions::StdExpansion::GetBoundaryMap
void GetBoundaryMap(Array< OneD, unsigned int > &outarray)
Definition: StdExpansion.h:790
void Nektar::LocalRegions::TetExp::GeneralMatrixOp_MatOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
private

Definition at line 1518 of file TetExp.cpp.

References Nektar::LocalRegions::Expansion::GetLocMatrix(), Nektar::StdRegions::StdExpansion::m_ncoeffs, and Vmath::Vcopy().

1522  {
1523  DNekScalMatSharedPtr mat = GetLocMatrix(mkey);
1524 
1525  if(inarray.get() == outarray.get())
1526  {
1527  Array<OneD,NekDouble> tmp(m_ncoeffs);
1528  Vmath::Vcopy(m_ncoeffs,inarray.get(),1,tmp.get(),1);
1529 
1530  Blas::Dgemv('N',m_ncoeffs,m_ncoeffs,mat->Scale(),(mat->GetOwnedMatrix())->GetPtr().get(),
1531  m_ncoeffs, tmp.get(), 1, 0.0, outarray.get(), 1);
1532  }
1533  else
1534  {
1535  Blas::Dgemv('N',m_ncoeffs,m_ncoeffs,mat->Scale(),(mat->GetOwnedMatrix())->GetPtr().get(),
1536  m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
1537  }
1538  }
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::LocalRegions::Expansion::GetLocMatrix
DNekScalMatSharedPtr GetLocMatrix(const LocalRegions::MatrixKey &mkey)
Definition: Expansion.cpp:83
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1038
void Nektar::LocalRegions::TetExp::SetUpInverseTransformationMatrix ( const DNekMatSharedPtr &  m_transformationmatrix,
DNekMatSharedPtr  m_inversetransformationmatrix,
DNekMatSharedPtr  m_inversetransposedtransformationmatrix 
)
protected
void Nektar::LocalRegions::TetExp::v_ComputeConditionNumberOfMatrix ( const DNekScalMatSharedPtr &  mat)
protected
void Nektar::LocalRegions::TetExp::v_ComputeFaceNormal ( const int  face)
protectedvirtual

Compute the normal of a triangular face.

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 730 of file TetExp.cpp.

References ASSERTL0, Nektar::StdRegions::StdExpansion::DetFaceBasisKey(), Nektar::SpatialDomains::eMovingRegular, Nektar::SpatialDomains::eRegular, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetCoordim(), Nektar::LocalRegions::Expansion::GetGeom(), Nektar::LibUtilities::BasisKey::GetNumPoints(), Nektar::LibUtilities::BasisKey::GetPointsKey(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::LibUtilities::Interp2D(), Nektar::StdRegions::StdExpansion3D::m_faceNormals, Vmath::Sdiv(), Vmath::Vmul(), Vmath::Vsqrt(), Vmath::Vvtvp(), and Vmath::Zero().

731  {
732  int i;
733  const SpatialDomains::GeomFactorsSharedPtr &geomFactors =
734  GetGeom()->GetMetricInfo();
735  LibUtilities::PointsKeyVector ptsKeys = GetPointsKeys();
736  SpatialDomains::GeomType type = geomFactors->GetGtype();
737  const Array<TwoD, const NekDouble> &df = geomFactors->GetDerivFactors(ptsKeys);
738  const Array<OneD, const NekDouble> &jac = geomFactors->GetJac(ptsKeys);
739 
740  LibUtilities::BasisKey tobasis0 = DetFaceBasisKey(face,0);
741  LibUtilities::BasisKey tobasis1 = DetFaceBasisKey(face,1);
742 
743  // number of face quadrature points
744  int nq_face = tobasis0.GetNumPoints()*tobasis1.GetNumPoints();
745 
746  int vCoordDim = GetCoordim();
747 
748  m_faceNormals[face] = Array<OneD, Array<OneD, NekDouble> >(vCoordDim);
749  Array<OneD, Array<OneD, NekDouble> > &normal = m_faceNormals[face];
750  for (i = 0; i < vCoordDim; ++i)
751  {
752  normal[i] = Array<OneD, NekDouble>(nq_face);
753  }
754 
755  // Regular geometry case
756  if (type == SpatialDomains::eRegular ||
757  type == SpatialDomains::eMovingRegular)
758  {
759  NekDouble fac;
760 
761  // Set up normals
762  switch (face)
763  {
764  case 0:
765  {
766  for (i = 0; i < vCoordDim; ++i)
767  {
768  normal[i][0] = -df[3*i+2][0];
769  }
770 
771  break;
772  }
773  case 1:
774  {
775  for (i = 0; i < vCoordDim; ++i)
776  {
777  normal[i][0] = -df[3*i+1][0];
778  }
779 
780  break;
781  }
782  case 2:
783  {
784  for (i = 0; i < vCoordDim; ++i)
785  {
786  normal[i][0] = df[3*i][0]+df[3*i+1][0]+
787  df[3*i+2][0];
788  }
789 
790  break;
791  }
792  case 3:
793  {
794  for(i = 0; i < vCoordDim; ++i)
795  {
796  normal[i][0] = -df[3*i][0];
797  }
798  break;
799  }
800  default:
801  ASSERTL0(false,"face is out of range (edge < 3)");
802  }
803 
804  // normalise
805  fac = 0.0;
806  for (i = 0; i < vCoordDim; ++i)
807  {
808  fac += normal[i][0]*normal[i][0];
809  }
810  fac = 1.0/sqrt(fac);
811 
812  for (i = 0; i < vCoordDim; ++i)
813  {
814  Vmath::Fill(nq_face,fac*normal[i][0],normal[i],1);
815  }
816  }
817  else
818  {
819  // Set up deformed normals
820  int j, k;
821 
822  int nq0 = ptsKeys[0].GetNumPoints();
823  int nq1 = ptsKeys[1].GetNumPoints();
824  int nq2 = ptsKeys[2].GetNumPoints();
825  int nqtot;
826  int nq01 =nq0*nq1;
827 
828  // number of elemental quad points
829  if (face == 0)
830  {
831  nqtot = nq01;
832  }
833  else if (face == 1)
834  {
835  nqtot = nq0*nq2;
836  }
837  else
838  {
839  nqtot = nq1*nq2;
840  }
841 
842  LibUtilities::PointsKey points0;
843  LibUtilities::PointsKey points1;
844 
845  Array<OneD, NekDouble> faceJac(nqtot);
846  Array<OneD,NekDouble> normals(vCoordDim*nqtot, 0.0);
847 
848  // Extract Jacobian along face and recover local derivates
849  // (dx/dr) for polynomial interpolation by multiplying m_gmat by
850  // jacobian
851  switch (face)
852  {
853  case 0:
854  {
855  for(j = 0; j < nq01; ++j)
856  {
857  normals[j] = -df[2][j]*jac[j];
858  normals[nqtot+j] = -df[5][j]*jac[j];
859  normals[2*nqtot+j] = -df[8][j]*jac[j];
860  faceJac[j] = jac[j];
861  }
862 
863  points0 = ptsKeys[0];
864  points1 = ptsKeys[1];
865  break;
866  }
867 
868  case 1:
869  {
870  for (j = 0; j < nq0; ++j)
871  {
872  for(k = 0; k < nq2; ++k)
873  {
874  int tmp = j+nq01*k;
875  normals[j+k*nq0] =
876  -df[1][tmp]*jac[tmp];
877  normals[nqtot+j+k*nq0] =
878  -df[4][tmp]*jac[tmp];
879  normals[2*nqtot+j+k*nq0] =
880  -df[7][tmp]*jac[tmp];
881  faceJac[j+k*nq0] = jac[tmp];
882  }
883  }
884 
885  points0 = ptsKeys[0];
886  points1 = ptsKeys[2];
887  break;
888  }
889 
890  case 2:
891  {
892  for (j = 0; j < nq1; ++j)
893  {
894  for(k = 0; k < nq2; ++k)
895  {
896  int tmp = nq0-1+nq0*j+nq01*k;
897  normals[j+k*nq1] =
898  (df[0][tmp]+df[1][tmp]+df[2][tmp])*
899  jac[tmp];
900  normals[nqtot+j+k*nq1] =
901  (df[3][tmp]+df[4][tmp]+df[5][tmp])*
902  jac[tmp];
903  normals[2*nqtot+j+k*nq1] =
904  (df[6][tmp]+df[7][tmp]+df[8][tmp])*
905  jac[tmp];
906  faceJac[j+k*nq1] = jac[tmp];
907  }
908  }
909 
910  points0 = ptsKeys[1];
911  points1 = ptsKeys[2];
912  break;
913  }
914 
915  case 3:
916  {
917  for (j = 0; j < nq1; ++j)
918  {
919  for(k = 0; k < nq2; ++k)
920  {
921  int tmp = j*nq0+nq01*k;
922  normals[j+k*nq1] =
923  -df[0][tmp]*jac[tmp];
924  normals[nqtot+j+k*nq1] =
925  -df[3][tmp]*jac[tmp];
926  normals[2*nqtot+j+k*nq1] =
927  -df[6][tmp]*jac[tmp];
928  faceJac[j+k*nq1] = jac[tmp];
929  }
930  }
931 
932  points0 = ptsKeys[1];
933  points1 = ptsKeys[2];
934  break;
935  }
936 
937  default:
938  ASSERTL0(false,"face is out of range (face < 3)");
939  }
940 
941  Array<OneD,NekDouble> work (nq_face, 0.0);
942  // Interpolate Jacobian and invert
943  LibUtilities::Interp2D(points0, points1, faceJac,
944  tobasis0.GetPointsKey(),
945  tobasis1.GetPointsKey(),
946  work);
947  Vmath::Sdiv(nq_face, 1.0, &work[0], 1, &work[0], 1);
948 
949  // Interpolate normal and multiply by inverse Jacobian.
950  for(i = 0; i < vCoordDim; ++i)
951  {
952  LibUtilities::Interp2D(points0, points1,
953  &normals[i*nqtot],
954  tobasis0.GetPointsKey(),
955  tobasis1.GetPointsKey(),
956  &normal[i][0]);
957  Vmath::Vmul(nq_face,work,1,normal[i],1,normal[i],1);
958  }
959 
960  // Normalise to obtain unit normals.
961  Vmath::Zero(nq_face,work,1);
962  for(i = 0; i < GetCoordim(); ++i)
963  {
964  Vmath::Vvtvp(nq_face,normal[i],1,normal[i],1,work,1,work,1);
965  }
966 
967  Vmath::Vsqrt(nq_face,work,1,work,1);
968  Vmath::Sdiv (nq_face,1.0,work,1,work,1);
969 
970  for(i = 0; i < GetCoordim(); ++i)
971  {
972  Vmath::Vmul(nq_face,normal[i],1,work,1,normal[i],1);
973  }
974  }
975  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1276
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::LibUtilities::PointsKeyVector
std::vector< PointsKey > PointsKeyVector
Definition: Points.h:220
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Vmath::Sdiv
void Sdiv(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha/y.
Definition: Vmath.cpp:257
Nektar::LibUtilities::Interp2D
void Interp2D(const BasisKey &fbasis0, const BasisKey &fbasis1, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, Array< OneD, NekDouble > &to)
this function interpolates a 2D function evaluated at the quadrature points of the 2D basis...
Definition: Interp.cpp:116
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:43
Nektar::StdRegions::StdExpansion3D::m_faceNormals
std::map< int, NormalVector > m_faceNormals
Definition: StdExpansion3D.h:196
Nektar::LocalRegions::Expansion::GetGeom
SpatialDomains::GeometrySharedPtr GetGeom() const
Definition: Expansion.cpp:148
Nektar::SpatialDomains::GeomFactorsSharedPtr
boost::shared_ptr< GeomFactors > GeomFactorsSharedPtr
Pointer to a GeomFactors object.
Definition: GeomFactors.h:62
Nektar::SpatialDomains::eRegular
Geometry is straight-sided with constant geometric factors.
Definition: SpatialDomains.hpp:55
Nektar::StdRegions::StdExpansion::DetFaceBasisKey
const LibUtilities::BasisKey DetFaceBasisKey(const int i, const int k) const
Definition: StdExpansion.h:324
Nektar::SpatialDomains::GeomType
GeomType
Indicates the type of element geometry.
Definition: SpatialDomains.hpp:52
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::TetExp::v_ComputeLaplacianMetric ( )
protectedvirtual

Reimplemented from Nektar::LocalRegions::Expansion.

Definition at line 1611 of file TetExp.cpp.

References Nektar::LocalRegions::Expansion::ComputeQuadratureMetric(), Nektar::SpatialDomains::eDeformed, Nektar::LocalRegions::eMetricLaplacian00, Nektar::LocalRegions::eMetricLaplacian01, Nektar::LocalRegions::eMetricLaplacian02, Nektar::LocalRegions::eMetricLaplacian11, Nektar::LocalRegions::eMetricLaplacian12, Nektar::LocalRegions::eMetricLaplacian22, Nektar::LocalRegions::eMetricQuadrature, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetTotPoints(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Nektar::LocalRegions::Expansion::m_metrics, Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric(), Vmath::Svtsvtp(), Vmath::Svtvp(), Vmath::Vadd(), Vmath::Vvtvp(), and Vmath::Vvtvvtp().

1612  {
1613  if (m_metrics.count(eMetricQuadrature) == 0)
1614  {
1615  ComputeQuadratureMetric();
1616  }
1617 
1618  int i, j;
1619  const unsigned int nqtot = GetTotPoints();
1620  const unsigned int dim = 3;
1621  const MetricType m[3][3] = { {eMetricLaplacian00, eMetricLaplacian01, eMetricLaplacian02},
1622  {eMetricLaplacian01, eMetricLaplacian11, eMetricLaplacian12},
1623  {eMetricLaplacian02, eMetricLaplacian12, eMetricLaplacian22}
1624  };
1625 
1626  for (unsigned int i = 0; i < dim; ++i)
1627  {
1628  for (unsigned int j = i; j < dim; ++j)
1629  {
1630  m_metrics[m[i][j]] = Array<OneD, NekDouble>(nqtot);
1631  }
1632  }
1633 
1634  // Define shorthand synonyms for m_metrics storage
1635  Array<OneD,NekDouble> g0 (m_metrics[m[0][0]]);
1636  Array<OneD,NekDouble> g1 (m_metrics[m[1][1]]);
1637  Array<OneD,NekDouble> g2 (m_metrics[m[2][2]]);
1638  Array<OneD,NekDouble> g3 (m_metrics[m[0][1]]);
1639  Array<OneD,NekDouble> g4 (m_metrics[m[0][2]]);
1640  Array<OneD,NekDouble> g5 (m_metrics[m[1][2]]);
1641 
1642  // Allocate temporary storage
1643  Array<OneD,NekDouble> alloc(7*nqtot,0.0);
1644  Array<OneD,NekDouble> h0 (alloc); // h0
1645  Array<OneD,NekDouble> h1 (alloc+ 1*nqtot);// h1
1646  Array<OneD,NekDouble> h2 (alloc+ 2*nqtot);// h2
1647  Array<OneD,NekDouble> h3 (alloc+ 3*nqtot);// h3
1648  Array<OneD,NekDouble> wsp4 (alloc+ 4*nqtot);// wsp4
1649  Array<OneD,NekDouble> wsp5 (alloc+ 5*nqtot);// wsp5
1650  Array<OneD,NekDouble> wsp6 (alloc+ 6*nqtot);// wsp6
1651  // Reuse some of the storage as workspace
1652  Array<OneD,NekDouble> wsp7 (alloc); // wsp7
1653  Array<OneD,NekDouble> wsp8 (alloc+ 1*nqtot);// wsp8
1654  Array<OneD,NekDouble> wsp9 (alloc+ 2*nqtot);// wsp9
1655 
1656  const Array<TwoD, const NekDouble>& df =
1657  m_metricinfo->GetDerivFactors(GetPointsKeys());
1658  const Array<OneD, const NekDouble>& z0 = m_base[0]->GetZ();
1659  const Array<OneD, const NekDouble>& z1 = m_base[1]->GetZ();
1660  const Array<OneD, const NekDouble>& z2 = m_base[2]->GetZ();
1661  const unsigned int nquad0 = m_base[0]->GetNumPoints();
1662  const unsigned int nquad1 = m_base[1]->GetNumPoints();
1663  const unsigned int nquad2 = m_base[2]->GetNumPoints();
1664 
1665  for(j = 0; j < nquad2; ++j)
1666  {
1667  for(i = 0; i < nquad1; ++i)
1668  {
1669  Vmath::Fill(nquad0, 4.0/(1.0-z1[i])/(1.0-z2[j]), &h0[0]+i*nquad0 + j*nquad0*nquad1,1);
1670  Vmath::Fill(nquad0, 2.0/(1.0-z1[i])/(1.0-z2[j]), &h1[0]+i*nquad0 + j*nquad0*nquad1,1);
1671  Vmath::Fill(nquad0, 2.0/(1.0-z2[j]), &h2[0]+i*nquad0 + j*nquad0*nquad1,1);
1672  Vmath::Fill(nquad0, (1.0+z1[i])/(1.0-z2[j]), &h3[0]+i*nquad0 + j*nquad0*nquad1,1);
1673  }
1674  }
1675  for(i = 0; i < nquad0; i++)
1676  {
1677  Blas::Dscal(nquad1*nquad2, 1+z0[i], &h1[0]+i, nquad0);
1678  }
1679 
1680  // Step 3. Construct combined metric terms for physical space to
1681  // collapsed coordinate system.
1682  // Order of construction optimised to minimise temporary storage
1683  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1684  {
1685  // wsp4
1686  Vmath::Vadd(nqtot, &df[1][0], 1, &df[2][0], 1, &wsp4[0], 1);
1687  Vmath::Vvtvvtp(nqtot, &df[0][0], 1, &h0[0], 1, &wsp4[0], 1, &h1[0], 1, &wsp4[0], 1);
1688  // wsp5
1689  Vmath::Vadd(nqtot, &df[4][0], 1, &df[5][0], 1, &wsp5[0], 1);
1690  Vmath::Vvtvvtp(nqtot, &df[3][0], 1, &h0[0], 1, &wsp5[0], 1, &h1[0], 1, &wsp5[0], 1);
1691  // wsp6
1692  Vmath::Vadd(nqtot, &df[7][0], 1, &df[8][0], 1, &wsp6[0], 1);
1693  Vmath::Vvtvvtp(nqtot, &df[6][0], 1, &h0[0], 1, &wsp6[0], 1, &h1[0], 1, &wsp6[0], 1);
1694 
1695  // g0
1696  Vmath::Vvtvvtp(nqtot, &wsp4[0], 1, &wsp4[0], 1, &wsp5[0], 1, &wsp5[0], 1, &g0[0], 1);
1697  Vmath::Vvtvp (nqtot, &wsp6[0], 1, &wsp6[0], 1, &g0[0], 1, &g0[0], 1);
1698 
1699  // g4
1700  Vmath::Vvtvvtp(nqtot, &df[2][0], 1, &wsp4[0], 1, &df[5][0], 1, &wsp5[0], 1, &g4[0], 1);
1701  Vmath::Vvtvp (nqtot, &df[8][0], 1, &wsp6[0], 1, &g4[0], 1, &g4[0], 1);
1702 
1703  // overwrite h0, h1, h2
1704  // wsp7 (h2f1 + h3f2)
1705  Vmath::Vvtvvtp(nqtot, &df[1][0], 1, &h2[0], 1, &df[2][0], 1, &h3[0], 1, &wsp7[0], 1);
1706  // wsp8 (h2f4 + h3f5)
1707  Vmath::Vvtvvtp(nqtot, &df[4][0], 1, &h2[0], 1, &df[5][0], 1, &h3[0], 1, &wsp8[0], 1);
1708  // wsp9 (h2f7 + h3f8)
1709  Vmath::Vvtvvtp(nqtot, &df[7][0], 1, &h2[0], 1, &df[8][0], 1, &h3[0], 1, &wsp9[0], 1);
1710 
1711  // g3
1712  Vmath::Vvtvvtp(nqtot, &wsp4[0], 1, &wsp7[0], 1, &wsp5[0], 1, &wsp8[0], 1, &g3[0], 1);
1713  Vmath::Vvtvp (nqtot, &wsp6[0], 1, &wsp9[0], 1, &g3[0], 1, &g3[0], 1);
1714 
1715  // overwrite wsp4, wsp5, wsp6
1716  // g1
1717  Vmath::Vvtvvtp(nqtot, &wsp7[0], 1, &wsp7[0], 1, &wsp8[0], 1, &wsp8[0], 1, &g1[0], 1);
1718  Vmath::Vvtvp (nqtot, &wsp9[0], 1, &wsp9[0], 1, &g1[0], 1, &g1[0], 1);
1719 
1720  // g5
1721  Vmath::Vvtvvtp(nqtot, &df[2][0], 1, &wsp7[0], 1, &df[5][0], 1, &wsp8[0], 1, &g5[0], 1);
1722  Vmath::Vvtvp (nqtot, &df[8][0], 1, &wsp9[0], 1, &g5[0], 1, &g5[0], 1);
1723 
1724  // g2
1725  Vmath::Vvtvvtp(nqtot, &df[2][0], 1, &df[2][0], 1, &df[5][0], 1, &df[5][0], 1, &g2[0], 1);
1726  Vmath::Vvtvp (nqtot, &df[8][0], 1, &df[8][0], 1, &g2[0], 1, &g2[0], 1);
1727  }
1728  else
1729  {
1730  // wsp4
1731  Vmath::Svtsvtp(nqtot, df[0][0], &h0[0], 1, df[1][0] + df[2][0], &h1[0], 1, &wsp4[0], 1);
1732  // wsp5
1733  Vmath::Svtsvtp(nqtot, df[3][0], &h0[0], 1, df[4][0] + df[5][0], &h1[0], 1, &wsp5[0], 1);
1734  // wsp6
1735  Vmath::Svtsvtp(nqtot, df[6][0], &h0[0], 1, df[7][0] + df[8][0], &h1[0], 1, &wsp6[0], 1);
1736 
1737  // g0
1738  Vmath::Vvtvvtp(nqtot, &wsp4[0], 1, &wsp4[0], 1, &wsp5[0], 1, &wsp5[0], 1, &g0[0], 1);
1739  Vmath::Vvtvp (nqtot, &wsp6[0], 1, &wsp6[0], 1, &g0[0], 1, &g0[0], 1);
1740 
1741  // g4
1742  Vmath::Svtsvtp(nqtot, df[2][0], &wsp4[0], 1, df[5][0], &wsp5[0], 1, &g4[0], 1);
1743  Vmath::Svtvp (nqtot, df[8][0], &wsp6[0], 1, &g4[0], 1, &g4[0], 1);
1744 
1745  // overwrite h0, h1, h2
1746  // wsp7 (h2f1 + h3f2)
1747  Vmath::Svtsvtp(nqtot, df[1][0], &h2[0], 1, df[2][0], &h3[0], 1, &wsp7[0], 1);
1748  // wsp8 (h2f4 + h3f5)
1749  Vmath::Svtsvtp(nqtot, df[4][0], &h2[0], 1, df[5][0], &h3[0], 1, &wsp8[0], 1);
1750  // wsp9 (h2f7 + h3f8)
1751  Vmath::Svtsvtp(nqtot, df[7][0], &h2[0], 1, df[8][0], &h3[0], 1, &wsp9[0], 1);
1752 
1753  // g3
1754  Vmath::Vvtvvtp(nqtot, &wsp4[0], 1, &wsp7[0], 1, &wsp5[0], 1, &wsp8[0], 1, &g3[0], 1);
1755  Vmath::Vvtvp (nqtot, &wsp6[0], 1, &wsp9[0], 1, &g3[0], 1, &g3[0], 1);
1756 
1757  // overwrite wsp4, wsp5, wsp6
1758  // g1
1759  Vmath::Vvtvvtp(nqtot, &wsp7[0], 1, &wsp7[0], 1, &wsp8[0], 1, &wsp8[0], 1, &g1[0], 1);
1760  Vmath::Vvtvp (nqtot, &wsp9[0], 1, &wsp9[0], 1, &g1[0], 1, &g1[0], 1);
1761 
1762  // g5
1763  Vmath::Svtsvtp(nqtot, df[2][0], &wsp7[0], 1, df[5][0], &wsp8[0], 1, &g5[0], 1);
1764  Vmath::Svtvp (nqtot, df[8][0], &wsp9[0], 1, &g5[0], 1, &g5[0], 1);
1765 
1766  // g2
1767  Vmath::Fill(nqtot, df[2][0]*df[2][0] + df[5][0]*df[5][0] + df[8][0]*df[8][0], &g2[0], 1);
1768  }
1769 
1770  for (unsigned int i = 0; i < dim; ++i)
1771  {
1772  for (unsigned int j = i; j < dim; ++j)
1773  {
1774  MultiplyByQuadratureMetric(m_metrics[m[i][j]],
1775  m_metrics[m[i][j]]);
1776 
1777  }
1778  }
1779 
1780 
1781  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1276
Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric
void MultiplyByQuadratureMetric(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:902
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Vmath::Svtvp
void Svtvp(int n, const T alpha, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
svtvp (scalar times vector plus vector): z = alpha*x + y
Definition: Vmath.cpp:471
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::StdRegions::StdExpansion::GetTotPoints
int GetTotPoints() const
This function returns the total number of quadrature points used in the element.
Definition: StdExpansion.h:141
Vmath::Vvtvvtp
void Vvtvvtp(int n, const T *v, int incv, const T *w, int incw, const T *x, int incx, const T *y, int incy, T *z, int incz)
vvtvvtp (vector times vector plus vector times vector):
Definition: Vmath.cpp:523
Vmath::Svtsvtp
void Svtsvtp(int n, const T alpha, const T *x, int incx, const T beta, const T *y, int incy, T *z, int incz)
vvtvvtp (scalar times vector plus scalar times vector):
Definition: Vmath.cpp:577
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
DNekMatSharedPtr Nektar::LocalRegions::TetExp::v_CreateStdMatrix ( const StdRegions::StdMatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 1492 of file TetExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::StdRegions::StdExpansion::m_base.

1494  {
1495  LibUtilities::BasisKey bkey0 = m_base[0]->GetBasisKey();
1496  LibUtilities::BasisKey bkey1 = m_base[1]->GetBasisKey();
1497  LibUtilities::BasisKey bkey2 = m_base[2]->GetBasisKey();
1498  StdRegions::StdTetExpSharedPtr tmp = MemoryManager<StdTetExp>::AllocateSharedPtr(bkey0, bkey1, bkey2);
1499 
1500  return tmp->GetStdMatrix(mkey);
1501  }
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::StdRegions::StdTetExpSharedPtr
boost::shared_ptr< StdTetExp > StdTetExpSharedPtr
Definition: StdTetExp.h:268
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
LibUtilities::ShapeType Nektar::LocalRegions::TetExp::v_DetShapeType ( ) const
protectedvirtual

Return Shape of region, using ShapeType enum list.

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 540 of file TetExp.cpp.

References Nektar::LibUtilities::eTetrahedron.

541  {
542  return LibUtilities::eTetrahedron;
543  }
void Nektar::LocalRegions::TetExp::v_DropLocStaticCondMatrix ( const MatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1513 of file TetExp.cpp.

References m_staticCondMatrixManager.

1514  {
1515  m_staticCondMatrixManager.DeleteObject(mkey);
1516  }
Nektar::LocalRegions::TetExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: TetExp.h:219
void Nektar::LocalRegions::TetExp::v_ExtractDataToCoeffs ( const NekDouble *  data,
const std::vector< unsigned int > &  nummodes,
const int  nmode_offset,
NekDouble *  coeffs 
)
protectedvirtual

Unpack data from input file assuming it comes from the same expansion type.

See also
StdExpansion::ExtractDataToCoeffs

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 558 of file TetExp.cpp.

References ASSERTL0, ASSERTL1, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::LibUtilities::eModified_C, Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion::m_ncoeffs, Vmath::Vcopy(), and Vmath::Zero().

563  {
564  int data_order0 = nummodes[mode_offset];
565  int fillorder0 = min(m_base[0]->GetNumModes(),data_order0);
566  int data_order1 = nummodes[mode_offset+1];
567  int order1 = m_base[1]->GetNumModes();
568  int fillorder1 = min(order1,data_order1);
569  int data_order2 = nummodes[mode_offset+2];
570  int order2 = m_base[2]->GetNumModes();
571  int fillorder2 = min(order2,data_order2);
572 
573  switch(m_base[0]->GetBasisType())
574  {
575  case LibUtilities::eModified_A:
576  {
577  int i,j;
578  int cnt = 0;
579  int cnt1 = 0;
580 
581  ASSERTL1(m_base[1]->GetBasisType() ==
582  LibUtilities::eModified_B,
583  "Extraction routine not set up for this basis");
584  ASSERTL1(m_base[2]->GetBasisType() ==
585  LibUtilities::eModified_C,
586  "Extraction routine not set up for this basis");
587 
588  Vmath::Zero(m_ncoeffs,coeffs,1);
589  for(j = 0; j < fillorder0; ++j)
590  {
591  for(i = 0; i < fillorder1-j; ++i)
592  {
593  Vmath::Vcopy(fillorder2-j-i, &data[cnt], 1,
594  &coeffs[cnt1], 1);
595  cnt += data_order2-j-i;
596  cnt1 += order2-j-i;
597  }
598 
599  // count out data for j iteration
600  for(i = fillorder1-j; i < data_order1-j; ++i)
601  {
602  cnt += data_order2-j-i;
603  }
604 
605  for(i = fillorder1-j; i < order1-j; ++i)
606  {
607  cnt1 += order2-j-i;
608  }
609 
610  }
611  }
612  break;
613  default:
614  ASSERTL0(false, "basis is either not set up or not "
615  "hierarchicial");
616  }
617  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::LibUtilities::eModified_C
Principle Modified Functions .
Definition: BasisType.h:51
Nektar::LibUtilities::eModified_A
Principle Modified Functions .
Definition: BasisType.h:49
Nektar::LibUtilities::eModified_B
Principle Modified Functions .
Definition: BasisType.h:50
Nektar::StdRegions::StdExpansion::GetBasisType
LibUtilities::BasisType GetBasisType(const int dir) const
This function returns the type of basis used in the dir direction.
Definition: StdExpansion.h:165
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1038
void Nektar::LocalRegions::TetExp::v_FwdTrans ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Forward transform from physical quadrature space stored in inarray and evaluate the expansion coefficients and store in (this)->_coeffs.

Parameters
inarrayArray of physical quadrature points to be transformed.
outarrayArray of coefficients to update.

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 233 of file TetExp.cpp.

References Nektar::StdRegions::StdTetExp::DetShapeType(), Nektar::StdRegions::eInvMass, Nektar::eWrapper, Nektar::StdRegions::StdExpansion::GetNcoeffs(), Nektar::StdRegions::StdExpansion::IProductWRTBase(), Nektar::StdRegions::StdExpansion::m_base, m_matrixManager, Nektar::StdRegions::StdExpansion::m_ncoeffs, and Vmath::Vcopy().

236  {
237  if((m_base[0]->Collocation())&&(m_base[1]->Collocation())&&(m_base[2]->Collocation()))
238  {
239  Vmath::Vcopy(GetNcoeffs(),&inarray[0],1,&outarray[0],1);
240  }
241  else
242  {
243  IProductWRTBase(inarray,outarray);
244 
245  // get Mass matrix inverse
246  MatrixKey masskey(StdRegions::eInvMass,
247  DetShapeType(),*this);
248  DNekScalMatSharedPtr matsys = m_matrixManager[masskey];
249 
250  // copy inarray in case inarray == outarray
251  DNekVec in (m_ncoeffs,outarray);
252  DNekVec out(m_ncoeffs,outarray,eWrapper);
253 
254  out = (*matsys)*in;
255  }
256  }
Nektar::StdRegions::StdExpansion::IProductWRTBase
void IProductWRTBase(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
this function calculates the inner product of a given function f with the different modes of the expa...
Definition: StdExpansion.h:613
Nektar::LocalRegions::TetExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: TetExp.h:218
Nektar::DNekScalMatSharedPtr
boost::shared_ptr< DNekScalMat > DNekScalMatSharedPtr
Definition: NekMatrixFwd.hpp:73
Nektar::StdRegions::StdTetExp::DetShapeType
LibUtilities::ShapeType DetShapeType() const
Definition: StdTetExp.h:70
Nektar::DNekVec
NekVector< NekDouble > DNekVec
Definition: NekTypeDefs.hpp:49
Nektar::StdRegions::StdExpansion::GetNcoeffs
int GetNcoeffs(void) const
This function returns the total number of coefficients used in the expansion.
Definition: StdExpansion.h:131
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1038
DNekMatSharedPtr Nektar::LocalRegions::TetExp::v_GenMatrix ( const StdRegions::StdMatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 1041 of file TetExp.cpp.

References Nektar::StdRegions::eHybridDGHelmBndLam, Nektar::StdRegions::eHybridDGHelmholtz, Nektar::StdRegions::eHybridDGLamToQ0, Nektar::StdRegions::eHybridDGLamToQ1, Nektar::StdRegions::eHybridDGLamToQ2, Nektar::StdRegions::eHybridDGLamToU, Nektar::StdRegions::eInvLaplacianWithUnityMean, Nektar::StdRegions::StdMatrixKey::GetMatrixType(), and Nektar::LocalRegions::Expansion3D::v_GenMatrix().

1043  {
1044  DNekMatSharedPtr returnval;
1045 
1046  switch(mkey.GetMatrixType())
1047  {
1048  case StdRegions::eHybridDGHelmholtz:
1049  case StdRegions::eHybridDGLamToU:
1050  case StdRegions::eHybridDGLamToQ0:
1051  case StdRegions::eHybridDGLamToQ1:
1052  case StdRegions::eHybridDGLamToQ2:
1053  case StdRegions::eHybridDGHelmBndLam:
1054  case StdRegions::eInvLaplacianWithUnityMean:
1055  returnval = Expansion3D::v_GenMatrix(mkey);
1056  break;
1057  default:
1058  returnval = StdTetExp::v_GenMatrix(mkey);
1059  }
1060 
1061  return returnval;
1062  }
Nektar::DNekMatSharedPtr
boost::shared_ptr< DNekMat > DNekMatSharedPtr
Definition: NekTypeDefs.hpp:70
Nektar::LocalRegions::Expansion3D::v_GenMatrix
virtual DNekMatSharedPtr v_GenMatrix(const StdRegions::StdMatrixKey &mkey)
Definition: Expansion3D.cpp:380
void Nektar::LocalRegions::TetExp::v_GetCoord ( const Array< OneD, const NekDouble > &  Lcoords,
Array< OneD, NekDouble > &  coords 
)
protectedvirtual

Get the coordinates "coords" at the local coordinates "Lcoords".

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 505 of file TetExp.cpp.

References ASSERTL1, and Nektar::LocalRegions::Expansion::m_geom.

508  {
509  int i;
510 
511  ASSERTL1(Lcoords[0] <= -1.0 && Lcoords[0] >= 1.0 &&
512  Lcoords[1] <= -1.0 && Lcoords[1] >= 1.0 &&
513  Lcoords[2] <= -1.0 && Lcoords[2] >= 1.0,
514  "Local coordinates are not in region [-1,1]");
515 
516  // m_geom->FillGeom(); // TODO: implement FillGeom()
517 
518  for(i = 0; i < m_geom->GetCoordim(); ++i)
519  {
520  coords[i] = m_geom->GetCoord(i,Lcoords);
521  }
522  }
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
int Nektar::LocalRegions::TetExp::v_GetCoordim ( void  )
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion3D.

Definition at line 553 of file TetExp.cpp.

References Nektar::LocalRegions::Expansion::m_geom.

554  {
555  return m_geom->GetCoordim();
556  }
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
void Nektar::LocalRegions::TetExp::v_GetCoords ( Array< OneD, NekDouble > &  coords_1,
Array< OneD, NekDouble > &  coords_2,
Array< OneD, NekDouble > &  coords_3 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 524 of file TetExp.cpp.

References Nektar::LocalRegions::Expansion::v_GetCoords().

528  {
529  Expansion::v_GetCoords(coords_0, coords_1, coords_2);
530  }
Nektar::LocalRegions::Expansion::v_GetCoords
virtual void v_GetCoords(Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2, Array< OneD, NekDouble > &coords_3)
Definition: Expansion.cpp:211
void Nektar::LocalRegions::TetExp::v_GetFacePhysVals ( const int  face,
const StdRegions::StdExpansionSharedPtr &  FaceExp,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
StdRegions::Orientation  orient 
)
protectedvirtual

Returns the physical values at the quadrature points of a face.

Definition at line 636 of file TetExp.cpp.

References ASSERTL0, Nektar::StdRegions::eNoOrientation, Nektar::StdRegions::StdExpansion::GetFaceNumPoints(), Nektar::StdRegions::StdExpansion::GetForient(), Nektar::LibUtilities::Interp2D(), Nektar::StdRegions::StdExpansion::m_base, and Vmath::Vcopy().

Referenced by v_GetTracePhysVals().

642  {
643  int nquad0 = m_base[0]->GetNumPoints();
644  int nquad1 = m_base[1]->GetNumPoints();
645  int nquad2 = m_base[2]->GetNumPoints();
646 
647  Array<OneD,NekDouble> o_tmp (GetFaceNumPoints(face));
648  Array<OneD,NekDouble> o_tmp2(FaceExp->GetTotPoints());
649  Array<OneD,NekDouble> o_tmp3;
650 
651  if (orient == StdRegions::eNoOrientation)
652  {
653  orient = GetForient(face);
654  }
655 
656  switch(face)
657  {
658  case 0:
659  {
660  //Directions A and B positive
661  Vmath::Vcopy(nquad0*nquad1,inarray.get(),1,o_tmp.get(),1);
662  //interpolate
663  LibUtilities::Interp2D(m_base[0]->GetPointsKey(),
664  m_base[1]->GetPointsKey(),
665  o_tmp.get(),
666  FaceExp->GetBasis(0)->GetPointsKey(),
667  FaceExp->GetBasis(1)->GetPointsKey(),
668  o_tmp2.get());
669  break;
670  }
671  case 1:
672  {
673  //Direction A and B positive
674  for (int k=0; k<nquad2; k++)
675  {
676  Vmath::Vcopy(nquad0,inarray.get()+(nquad0*nquad1*k),1,o_tmp.get()+(k*nquad0),1);
677  }
678  //interpolate
679  LibUtilities::Interp2D(m_base[0]->GetPointsKey(),
680  m_base[2]->GetPointsKey(),
681  o_tmp.get(),
682  FaceExp->GetBasis(0)->GetPointsKey(),
683  FaceExp->GetBasis(1)->GetPointsKey(),
684  o_tmp2.get());
685  break;
686  }
687  case 2:
688  {
689  //Directions A and B positive
690  Vmath::Vcopy(nquad1*nquad2,inarray.get()+(nquad0-1),nquad0,o_tmp.get(),1);
691  //interpolate
692  LibUtilities::Interp2D(m_base[1]->GetPointsKey(), m_base[2]->GetPointsKey(), o_tmp.get(),
693  FaceExp->GetBasis(0)->GetPointsKey(),FaceExp->GetBasis(1)->GetPointsKey(),o_tmp2.get());
694  break;
695  }
696  case 3:
697  {
698  //Directions A and B positive
699  Vmath::Vcopy(nquad1*nquad2,inarray.get(),nquad0,o_tmp.get(),1);
700  //interpolate
701  LibUtilities::Interp2D(m_base[1]->GetPointsKey(), m_base[2]->GetPointsKey(), o_tmp.get(),
702  FaceExp->GetBasis(0)->GetPointsKey(),FaceExp->GetBasis(1)->GetPointsKey(),o_tmp2.get());
703  }
704  break;
705  default:
706  ASSERTL0(false,"face value (> 3) is out of range");
707  break;
708  }
709 
710  int nq1 = FaceExp->GetNumPoints(0);
711  int nq2 = FaceExp->GetNumPoints(1);
712 
713  if ((int)orient == 7)
714  {
715  for (int j = 0; j < nq2; ++j)
716  {
717  Vmath::Vcopy(nq1, o_tmp2.get()+((j+1)*nq1-1), -1, outarray.get()+j*nq1, 1);
718  }
719  }
720  else
721  {
722  Vmath::Vcopy(nq1*nq2, o_tmp2.get(), 1, outarray.get(), 1);
723  }
724  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::StdRegions::StdExpansion::GetFaceNumPoints
int GetFaceNumPoints(const int i) const
This function returns the number of quadrature points belonging to the i-th face. ...
Definition: StdExpansion.h:339
Nektar::StdRegions::StdExpansion::GetForient
StdRegions::Orientation GetForient(int face)
Definition: StdExpansion.h:731
Nektar::LibUtilities::Interp2D
void Interp2D(const BasisKey &fbasis0, const BasisKey &fbasis1, const Array< OneD, const NekDouble > &from, const BasisKey &tbasis0, const BasisKey &tbasis1, Array< OneD, NekDouble > &to)
this function interpolates a 2D function evaluated at the quadrature points of the 2D basis...
Definition: Interp.cpp:116
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1038
DNekScalMatSharedPtr Nektar::LocalRegions::TetExp::v_GetLocMatrix ( const MatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::LocalRegions::Expansion.

Definition at line 1503 of file TetExp.cpp.

References m_matrixManager.

1504  {
1505  return m_matrixManager[mkey];
1506  }
Nektar::LocalRegions::TetExp::m_matrixManager
LibUtilities::NekManager< MatrixKey, DNekScalMat, MatrixKey::opLess > m_matrixManager
Definition: TetExp.h:218
DNekScalBlkMatSharedPtr Nektar::LocalRegions::TetExp::v_GetLocStaticCondMatrix ( const MatrixKey &  mkey)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1508 of file TetExp.cpp.

References m_staticCondMatrixManager.

1509  {
1510  return m_staticCondMatrixManager[mkey];
1511  }
Nektar::LocalRegions::TetExp::m_staticCondMatrixManager
LibUtilities::NekManager< MatrixKey, DNekScalBlkMat, MatrixKey::opLess > m_staticCondMatrixManager
Definition: TetExp.h:219
StdRegions::StdExpansionSharedPtr Nektar::LocalRegions::TetExp::v_GetStdExp ( void  ) const
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 545 of file TetExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::StdRegions::StdExpansion::m_base.

546  {
547  return MemoryManager<StdRegions::StdTetExp>
548  ::AllocateSharedPtr(m_base[0]->GetBasisKey(),
549  m_base[1]->GetBasisKey(),
550  m_base[2]->GetBasisKey());
551  }
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
void Nektar::LocalRegions::TetExp::v_GetTracePhysVals ( const int  face,
const StdRegions::StdExpansionSharedPtr &  FaceExp,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
StdRegions::Orientation  orient 
)
protectedvirtual

Returns the physical values at the quadrature points of a face Wrapper function to v_GetFacePhysVals.

Definition at line 623 of file TetExp.cpp.

References v_GetFacePhysVals().

629  {
630  v_GetFacePhysVals(face,FaceExp,inarray,outarray,orient);
631  }
Nektar::LocalRegions::TetExp::v_GetFacePhysVals
virtual void v_GetFacePhysVals(const int face, const StdRegions::StdExpansionSharedPtr &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient)
Returns the physical values at the quadrature points of a face.
Definition: TetExp.cpp:636
void Nektar::LocalRegions::TetExp::v_HelmholtzMatrixOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 980 of file TetExp.cpp.

References Nektar::StdRegions::StdExpansion3D::v_HelmholtzMatrixOp_MatFree().

984  {
985  TetExp::v_HelmholtzMatrixOp_MatFree(inarray,outarray,mkey);
986  }
Nektar::StdRegions::StdExpansion3D::v_HelmholtzMatrixOp_MatFree
virtual void v_HelmholtzMatrixOp_MatFree(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
Definition: StdExpansion3D.cpp:248
NekDouble Nektar::LocalRegions::TetExp::v_Integral ( const Array< OneD, const NekDouble > &  inarray)
protectedvirtual

Integrate the physical point list inarray over region.

Parameters
inarrayDefinition of function to be returned at quadrature point of expansion.
Returns
$\int^1_{-1}\int^1_{-1} \int^1_{-1} u(\eta_1, \eta_2, \eta_3) J[i,j,k] d \eta_1 d \eta_2 d \eta_3 $ where $inarray[i,j,k] = u(\eta_{1i},\eta_{2j},\eta_{3k}) $ and $ J[i,j,k] $ is the Jacobian evaluated at the quadrature point.

Reimplemented from Nektar::StdRegions::StdExpansion3D.

Definition at line 114 of file TetExp.cpp.

References Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Smul(), and Vmath::Vmul().

116  {
117  int nquad0 = m_base[0]->GetNumPoints();
118  int nquad1 = m_base[1]->GetNumPoints();
119  int nquad2 = m_base[2]->GetNumPoints();
120  Array<OneD, const NekDouble> jac = m_metricinfo->GetJac(GetPointsKeys());
121  NekDouble retrunVal;
122  Array<OneD,NekDouble> tmp(nquad0*nquad1*nquad2);
123 
124  // multiply inarray with Jacobian
125  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
126  {
127  Vmath::Vmul(nquad0*nquad1*nquad2,&jac[0],1,
128  (NekDouble*)&inarray[0],1, &tmp[0],1);
129  }
130  else
131  {
132  Vmath::Smul(nquad0*nquad1*nquad2,(NekDouble) jac[0],
133  (NekDouble*)&inarray[0],1,&tmp[0],1);
134  }
135 
136  // call StdTetExp version;
137  retrunVal = StdTetExp::v_Integral(tmp);
138 
139  return retrunVal;
140  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1276
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:43
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::TetExp::v_IProductWRTBase ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Calculate the inner product of inarray with respect to the basis B=m_base0*m_base1*m_base2 and put into outarray:

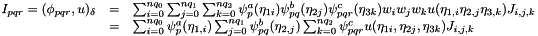
$ \begin{array}{rcl} I_{pqr} = (\phi_{pqr}, u)_{\delta} & = & \sum_{i=0}^{nq_0} \sum_{j=0}^{nq_1} \sum_{k=0}^{nq_2} \psi_{p}^{a} (\eta_{1i}) \psi_{pq}^{b} (\eta_{2j}) \psi_{pqr}^{c} (\eta_{3k}) w_i w_j w_k u(\eta_{1,i} \eta_{2,j} \eta_{3,k}) J_{i,j,k}\\ & = & \sum_{i=0}^{nq_0} \psi_p^a(\eta_{1,i}) \sum_{j=0}^{nq_1} \psi_{pq}^b(\eta_{2,j}) \sum_{k=0}^{nq_2} \psi_{pqr}^c u(\eta_{1i},\eta_{2j},\eta_{3k}) J_{i,j,k} \end{array} $
where 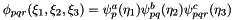$ \phi_{pqr} (\xi_1 , \xi_2 , \xi_3) = \psi_p^a (\eta_1) \psi_{pq}^b (\eta_2) \psi_{pqr}^c (\eta_3) $ which can be implemented as
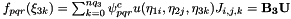
$f_{pqr} (\xi_{3k}) = \sum_{k=0}^{nq_3} \psi_{pqr}^c u(\eta_{1i},\eta_{2j},\eta_{3k}) J_{i,j,k} = {\bf B_3 U} $
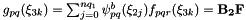
$ g_{pq} (\xi_{3k}) = \sum_{j=0}^{nq_1} \psi_{pq}^b (\xi_{2j}) f_{pqr} (\xi_{3k}) = {\bf B_2 F} $
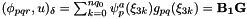
$ (\phi_{pqr}, u)_{\delta} = \sum_{k=0}^{nq_0} \psi_{p}^a (\xi_{3k}) g_{pq} (\xi_{3k}) = {\bf B_1 G} $

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 287 of file TetExp.cpp.

References v_IProductWRTBase_SumFac().

290  {
291  v_IProductWRTBase_SumFac(inarray, outarray);
292  }
Nektar::LocalRegions::TetExp::v_IProductWRTBase_SumFac
virtual void v_IProductWRTBase_SumFac(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)
Definition: TetExp.cpp:294
void Nektar::LocalRegions::TetExp::v_IProductWRTBase_SumFac ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
bool  multiplybyweights = true 
)
protectedvirtual
Parameters
inarrayFunction evaluated at physical collocation points.
outarrayInner product with respect to each basis function over the element.

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 294 of file TetExp.cpp.

References Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, and Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric().

Referenced by v_IProductWRTBase().

298  {
299  const int nquad0 = m_base[0]->GetNumPoints();
300  const int nquad1 = m_base[1]->GetNumPoints();
301  const int nquad2 = m_base[2]->GetNumPoints();
302  const int order0 = m_base[0]->GetNumModes();
303  const int order1 = m_base[1]->GetNumModes();
304  Array<OneD, NekDouble> wsp(nquad1*nquad2*order0 +
305  nquad2*order0*(order1+1)/2);
306 
307  if(multiplybyweights)
308  {
309  Array<OneD, NekDouble> tmp(nquad0*nquad1*nquad2);
310 
311  MultiplyByQuadratureMetric(inarray, tmp);
312  IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
313  m_base[1]->GetBdata(),
314  m_base[2]->GetBdata(),
315  tmp,outarray,wsp,
316  true,true,true);
317  }
318  else
319  {
320  IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
321  m_base[1]->GetBdata(),
322  m_base[2]->GetBdata(),
323  inarray,outarray,wsp,
324  true,true,true);
325  }
326  }
Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric
void MultiplyByQuadratureMetric(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:902
Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel
void IProductWRTBase_SumFacKernel(const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)
Definition: StdExpansion3D.cpp:127
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
void Nektar::LocalRegions::TetExp::v_IProductWRTDerivBase ( const int  dir,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray 
)
protectedvirtual

Calculates the inner product 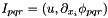$ I_{pqr} = (u, \partial_{x_i} \phi_{pqr}) $.

The derivative of the basis functions is performed using the chain rule in order to incorporate the geometric factors. Assuming that the basis functions are a tensor product 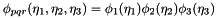$\phi_{pqr}(\eta_1,\eta_2,\eta_3) = \phi_1(\eta_1)\phi_2(\eta_2)\phi_3(\eta_3)$, this yields the result

\[ I_{pqr} = \sum_{j=1}^3 \left(u, \frac{\partial u}{\partial \eta_j} \frac{\partial \eta_j}{\partial x_i}\right) \]

In the prismatic element, we must also incorporate a second set of geometric factors which incorporate the collapsed co-ordinate system, so that

\[ \frac{\partial\eta_j}{\partial x_i} = \sum_{k=1}^3 \frac{\partial\eta_j}{\partial\xi_k}\frac{\partial\xi_k}{\partial x_i} \]

These derivatives can be found on p152 of Sherwin & Karniadakis.

Parameters
dirDirection in which to take the derivative.
inarrayThe function $ u $.
outarrayValue of the inner product.

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 358 of file TetExp.cpp.

References Nektar::SpatialDomains::eDeformed, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Nektar::StdRegions::StdExpansion::m_ncoeffs, Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric(), Vmath::Smul(), Vmath::Vadd(), Vmath::Vmul(), Vmath::Vvtvp(), and Vmath::Vvtvvtp().

362  {
363  const int nquad0 = m_base[0]->GetNumPoints();
364  const int nquad1 = m_base[1]->GetNumPoints();
365  const int nquad2 = m_base[2]->GetNumPoints();
366  const int order0 = m_base[0]->GetNumModes ();
367  const int order1 = m_base[1]->GetNumModes ();
368  const int nqtot = nquad0*nquad1*nquad2;
369  int i, j;
370 
371  const Array<OneD, const NekDouble> &z0 = m_base[0]->GetZ();
372  const Array<OneD, const NekDouble> &z1 = m_base[1]->GetZ();
373  const Array<OneD, const NekDouble> &z2 = m_base[2]->GetZ();
374 
375  Array<OneD, NekDouble> h0 (nqtot);
376  Array<OneD, NekDouble> h1 (nqtot);
377  Array<OneD, NekDouble> h2 (nqtot);
378  Array<OneD, NekDouble> h3 (nqtot);
379  Array<OneD, NekDouble> tmp1 (nqtot);
380  Array<OneD, NekDouble> tmp2 (nqtot);
381  Array<OneD, NekDouble> tmp3 (nqtot);
382  Array<OneD, NekDouble> tmp4 (nqtot);
383  Array<OneD, NekDouble> tmp5 (nqtot);
384  Array<OneD, NekDouble> tmp6 (m_ncoeffs);
385  Array<OneD, NekDouble> wsp (nquad1*nquad2*order0 +
386  nquad2*order0*(order1+1)/2);
387 
388  const Array<TwoD, const NekDouble>& df =
389  m_metricinfo->GetDerivFactors(GetPointsKeys());
390 
391  MultiplyByQuadratureMetric(inarray,tmp1);
392 
393  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
394  {
395  Vmath::Vmul(nqtot,&df[3*dir][0], 1,tmp1.get(),1,tmp2.get(),1);
396  Vmath::Vmul(nqtot,&df[3*dir+1][0],1,tmp1.get(),1,tmp3.get(),1);
397  Vmath::Vmul(nqtot,&df[3*dir+2][0],1,tmp1.get(),1,tmp4.get(),1);
398  }
399  else
400  {
401  Vmath::Smul(nqtot, df[3*dir ][0],tmp1.get(),1,tmp2.get(), 1);
402  Vmath::Smul(nqtot, df[3*dir+1][0],tmp1.get(),1,tmp3.get(), 1);
403  Vmath::Smul(nqtot, df[3*dir+2][0],tmp1.get(),1,tmp4.get(), 1);
404  }
405 
406  const int nq01 = nquad0*nquad1;
407  const int nq12 = nquad1*nquad2;
408 
409  for(j = 0; j < nquad2; ++j)
410  {
411  for(i = 0; i < nquad1; ++i)
412  {
413  Vmath::Fill(nquad0, 4.0/(1.0-z1[i])/(1.0-z2[j]),
414  &h0[0]+i*nquad0 + j*nq01,1);
415  Vmath::Fill(nquad0, 2.0/(1.0-z1[i])/(1.0-z2[j]),
416  &h1[0]+i*nquad0 + j*nq01,1);
417  Vmath::Fill(nquad0, 2.0/(1.0-z2[j]),
418  &h2[0]+i*nquad0 + j*nq01,1);
419  Vmath::Fill(nquad0, (1.0+z1[i])/(1.0-z2[j]),
420  &h3[0]+i*nquad0 + j*nq01,1);
421  }
422  }
423 
424  for(i = 0; i < nquad0; i++)
425  {
426  Blas::Dscal(nq12, 1+z0[i], &h1[0]+i, nquad0);
427  }
428 
429  // Assemble terms for first IP.
430  Vmath::Vvtvvtp(nqtot, &tmp2[0], 1, &h0[0], 1,
431  &tmp3[0], 1, &h1[0], 1,
432  &tmp5[0], 1);
433  Vmath::Vvtvp (nqtot, &tmp4[0], 1, &h1[0], 1,
434  &tmp5[0], 1, &tmp5[0], 1);
435 
436  IProductWRTBase_SumFacKernel(m_base[0]->GetDbdata(),
437  m_base[1]->GetBdata (),
438  m_base[2]->GetBdata (),
439  tmp5,outarray,wsp,
440  true,true,true);
441 
442  // Assemble terms for second IP.
443  Vmath::Vvtvvtp(nqtot, &tmp3[0], 1, &h2[0], 1,
444  &tmp4[0], 1, &h3[0], 1,
445  &tmp5[0], 1);
446 
447  IProductWRTBase_SumFacKernel(m_base[0]->GetBdata (),
448  m_base[1]->GetDbdata(),
449  m_base[2]->GetBdata (),
450  tmp5,tmp6,wsp,
451  true,true,true);
452  Vmath::Vadd(m_ncoeffs, tmp6, 1, outarray, 1, outarray, 1);
453 
454  // Do third IP.
455  IProductWRTBase_SumFacKernel(m_base[0]->GetBdata (),
456  m_base[1]->GetBdata (),
457  m_base[2]->GetDbdata(),
458  tmp4,tmp6,wsp,
459  true,true,true);
460 
461  // Sum contributions.
462  Vmath::Vadd(m_ncoeffs, tmp6, 1, outarray, 1, outarray, 1);
463  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1276
Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric
void MultiplyByQuadratureMetric(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
Definition: StdExpansion.h:902
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel
void IProductWRTBase_SumFacKernel(const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)
Definition: StdExpansion3D.cpp:127
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Vmath::Vvtvvtp
void Vvtvvtp(int n, const T *v, int incv, const T *w, int incw, const T *x, int incx, const T *y, int incy, T *z, int incz)
vvtvvtp (vector times vector plus vector times vector):
Definition: Vmath.cpp:523
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::LocalRegions::TetExp::v_LaplacianMatrixOp ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 989 of file TetExp.cpp.

References Nektar::StdRegions::StdExpansion3D::v_LaplacianMatrixOp_MatFree().

993  {
994  TetExp::v_LaplacianMatrixOp_MatFree(inarray,outarray,mkey);
995  }
Nektar::StdRegions::StdExpansion3D::v_LaplacianMatrixOp_MatFree
virtual void v_LaplacianMatrixOp_MatFree(const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)
Definition: StdExpansion3D.cpp:206
void Nektar::LocalRegions::TetExp::v_LaplacianMatrixOp ( const int  k1,
const int  k2,
const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 997 of file TetExp.cpp.

1003  {
1004  StdExpansion::LaplacianMatrixOp_MatFree(k1,k2,inarray,outarray,
1005  mkey);
1006  }
void Nektar::LocalRegions::TetExp::v_LaplacianMatrixOp_MatFree_Kernel ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  outarray,
Array< OneD, NekDouble > &  wsp 
)
privatevirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1541 of file TetExp.cpp.

References ASSERTL1, Nektar::LocalRegions::Expansion::ComputeLaplacianMetric(), Nektar::LocalRegions::eMetricLaplacian00, Nektar::LocalRegions::eMetricLaplacian01, Nektar::LocalRegions::eMetricLaplacian02, Nektar::LocalRegions::eMetricLaplacian11, Nektar::LocalRegions::eMetricLaplacian12, Nektar::LocalRegions::eMetricLaplacian22, Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metrics, Nektar::StdRegions::StdExpansion::m_ncoeffs, Vmath::Vadd(), Vmath::Vvtvp(), and Vmath::Vvtvvtp().

1545  {
1546  // This implementation is only valid when there are no
1547  // coefficients associated to the Laplacian operator
1548  if (m_metrics.count(eMetricLaplacian00) == 0)
1549  {
1550  ComputeLaplacianMetric();
1551  }
1552 
1553  int nquad0 = m_base[0]->GetNumPoints();
1554  int nquad1 = m_base[1]->GetNumPoints();
1555  int nquad2 = m_base[2]->GetNumPoints();
1556  int nqtot = nquad0*nquad1*nquad2;
1557 
1558  ASSERTL1(wsp.num_elements() >= 6*nqtot,
1559  "Insufficient workspace size.");
1560  ASSERTL1(m_ncoeffs <= nqtot,
1561  "Workspace not set up for ncoeffs > nqtot");
1562 
1563  const Array<OneD, const NekDouble>& base0 = m_base[0]->GetBdata();
1564  const Array<OneD, const NekDouble>& base1 = m_base[1]->GetBdata();
1565  const Array<OneD, const NekDouble>& base2 = m_base[2]->GetBdata();
1566  const Array<OneD, const NekDouble>& dbase0 = m_base[0]->GetDbdata();
1567  const Array<OneD, const NekDouble>& dbase1 = m_base[1]->GetDbdata();
1568  const Array<OneD, const NekDouble>& dbase2 = m_base[2]->GetDbdata();
1569  const Array<OneD, const NekDouble>& metric00 = m_metrics[eMetricLaplacian00];
1570  const Array<OneD, const NekDouble>& metric01 = m_metrics[eMetricLaplacian01];
1571  const Array<OneD, const NekDouble>& metric02 = m_metrics[eMetricLaplacian02];
1572  const Array<OneD, const NekDouble>& metric11 = m_metrics[eMetricLaplacian11];
1573  const Array<OneD, const NekDouble>& metric12 = m_metrics[eMetricLaplacian12];
1574  const Array<OneD, const NekDouble>& metric22 = m_metrics[eMetricLaplacian22];
1575 
1576  // Allocate temporary storage
1577  Array<OneD,NekDouble> wsp0 (2*nqtot, wsp);
1578  Array<OneD,NekDouble> wsp1 ( nqtot, wsp+1*nqtot);
1579  Array<OneD,NekDouble> wsp2 ( nqtot, wsp+2*nqtot);
1580  Array<OneD,NekDouble> wsp3 ( nqtot, wsp+3*nqtot);
1581  Array<OneD,NekDouble> wsp4 ( nqtot, wsp+4*nqtot);
1582  Array<OneD,NekDouble> wsp5 ( nqtot, wsp+5*nqtot);
1583 
1584  // LAPLACIAN MATRIX OPERATION
1585  // wsp1 = du_dxi1 = D_xi1 * inarray = D_xi1 * u
1586  // wsp2 = du_dxi2 = D_xi2 * inarray = D_xi2 * u
1587  // wsp2 = du_dxi3 = D_xi3 * inarray = D_xi3 * u
1588  StdExpansion3D::PhysTensorDeriv(inarray,wsp0,wsp1,wsp2);
1589 
1590  // wsp0 = k = g0 * wsp1 + g1 * wsp2 = g0 * du_dxi1 + g1 * du_dxi2
1591  // wsp2 = l = g1 * wsp1 + g2 * wsp2 = g0 * du_dxi1 + g1 * du_dxi2
1592  // where g0, g1 and g2 are the metric terms set up in the GeomFactors class
1593  // especially for this purpose
1594  Vmath::Vvtvvtp(nqtot,&metric00[0],1,&wsp0[0],1,&metric01[0],1,&wsp1[0],1,&wsp3[0],1);
1595  Vmath::Vvtvp (nqtot,&metric02[0],1,&wsp2[0],1,&wsp3[0],1,&wsp3[0],1);
1596  Vmath::Vvtvvtp(nqtot,&metric01[0],1,&wsp0[0],1,&metric11[0],1,&wsp1[0],1,&wsp4[0],1);
1597  Vmath::Vvtvp (nqtot,&metric12[0],1,&wsp2[0],1,&wsp4[0],1,&wsp4[0],1);
1598  Vmath::Vvtvvtp(nqtot,&metric02[0],1,&wsp0[0],1,&metric12[0],1,&wsp1[0],1,&wsp5[0],1);
1599  Vmath::Vvtvp (nqtot,&metric22[0],1,&wsp2[0],1,&wsp5[0],1,&wsp5[0],1);
1600 
1601  // outarray = m = (D_xi1 * B)^T * k
1602  // wsp1 = n = (D_xi2 * B)^T * l
1603  IProductWRTBase_SumFacKernel(dbase0,base1,base2,wsp3,outarray,wsp0,false,true,true);
1604  IProductWRTBase_SumFacKernel(base0,dbase1,base2,wsp4,wsp2, wsp0,true,false,true);
1605  Vmath::Vadd(m_ncoeffs,wsp2.get(),1,outarray.get(),1,outarray.get(),1);
1606  IProductWRTBase_SumFacKernel(base0,base1,dbase2,wsp5,wsp2, wsp0,true,true,false);
1607  Vmath::Vadd(m_ncoeffs,wsp2.get(),1,outarray.get(),1,outarray.get(),1);
1608  }
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel
void IProductWRTBase_SumFacKernel(const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)
Definition: StdExpansion3D.cpp:127
Vmath::Vvtvvtp
void Vvtvvtp(int n, const T *v, int incv, const T *w, int incw, const T *x, int incx, const T *y, int incy, T *z, int incz)
vvtvvtp (vector times vector plus vector times vector):
Definition: Vmath.cpp:523
ASSERTL1
#define ASSERTL1(condition, msg)
Assert Level 1 – Debugging which is used whether in FULLDEBUG or DEBUG compilation mode...
Definition: ErrorUtil.hpp:191
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
void Nektar::LocalRegions::TetExp::v_PhysDeriv ( const Array< OneD, const NekDouble > &  inarray,
Array< OneD, NekDouble > &  out_d0,
Array< OneD, NekDouble > &  out_d1,
Array< OneD, NekDouble > &  out_d2 
)
protectedvirtual

Differentiate inarray in the three coordinate directions.

Parameters
inarrayInput array of values at quadrature points to be differentiated.
out_d0Derivative in first coordinate direction.
out_d1Derivative in second coordinate direction.
out_d2Derivative in third coordinate direction.

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 155 of file TetExp.cpp.

References Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Smul(), Vmath::Vmul(), and Vmath::Vvtvp().

160  {
161  int TotPts = m_base[0]->GetNumPoints()*m_base[1]->GetNumPoints()*
162  m_base[2]->GetNumPoints();
163 
164  Array<TwoD, const NekDouble> df =
165  m_metricinfo->GetDerivFactors(GetPointsKeys());
166  Array<OneD,NekDouble> Diff0 = Array<OneD,NekDouble>(3*TotPts);
167  Array<OneD,NekDouble> Diff1 = Diff0 + TotPts;
168  Array<OneD,NekDouble> Diff2 = Diff1 + TotPts;
169 
170  StdTetExp::v_PhysDeriv(inarray, Diff0, Diff1, Diff2);
171 
172  if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
173  {
174  if(out_d0.num_elements())
175  {
176  Vmath::Vmul (TotPts,&df[0][0],1,&Diff0[0],1, &out_d0[0], 1);
177  Vmath::Vvtvp (TotPts,&df[1][0],1,&Diff1[0],1, &out_d0[0], 1,&out_d0[0],1);
178  Vmath::Vvtvp (TotPts,&df[2][0],1,&Diff2[0],1, &out_d0[0], 1,&out_d0[0],1);
179  }
180 
181  if(out_d1.num_elements())
182  {
183  Vmath::Vmul (TotPts,&df[3][0],1,&Diff0[0],1, &out_d1[0], 1);
184  Vmath::Vvtvp (TotPts,&df[4][0],1,&Diff1[0],1, &out_d1[0], 1,&out_d1[0],1);
185  Vmath::Vvtvp (TotPts,&df[5][0],1,&Diff2[0],1, &out_d1[0], 1,&out_d1[0],1);
186  }
187 
188  if(out_d2.num_elements())
189  {
190  Vmath::Vmul (TotPts,&df[6][0],1,&Diff0[0],1, &out_d2[0], 1);
191  Vmath::Vvtvp (TotPts,&df[7][0],1,&Diff1[0],1, &out_d2[0], 1, &out_d2[0],1);
192  Vmath::Vvtvp (TotPts,&df[8][0],1,&Diff2[0],1, &out_d2[0], 1, &out_d2[0],1);
193  }
194  }
195  else // regular geometry
196  {
197  if(out_d0.num_elements())
198  {
199  Vmath::Smul (TotPts,df[0][0],&Diff0[0],1, &out_d0[0], 1);
200  Blas::Daxpy (TotPts,df[1][0],&Diff1[0],1, &out_d0[0], 1);
201  Blas::Daxpy (TotPts,df[2][0],&Diff2[0],1, &out_d0[0], 1);
202  }
203 
204  if(out_d1.num_elements())
205  {
206  Vmath::Smul (TotPts,df[3][0],&Diff0[0],1, &out_d1[0], 1);
207  Blas::Daxpy (TotPts,df[4][0],&Diff1[0],1, &out_d1[0], 1);
208  Blas::Daxpy (TotPts,df[5][0],&Diff2[0],1, &out_d1[0], 1);
209  }
210 
211  if(out_d2.num_elements())
212  {
213  Vmath::Smul (TotPts,df[6][0],&Diff0[0],1, &out_d2[0], 1);
214  Blas::Daxpy (TotPts,df[7][0],&Diff1[0],1, &out_d2[0], 1);
215  Blas::Daxpy (TotPts,df[8][0],&Diff2[0],1, &out_d2[0], 1);
216  }
217  }
218  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1276
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::StdRegions::StdExpansion::m_base
Array< OneD, LibUtilities::BasisSharedPtr > m_base
Definition: StdExpansion.h:1356
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
NekDouble Nektar::LocalRegions::TetExp::v_PhysEvaluate ( const Array< OneD, const NekDouble > &  coord,
const Array< OneD, const NekDouble > &  physvals 
)
protectedvirtual
Parameters
coordPhysical space coordinate
Returns
Evaluation of expansion at given coordinate.

Reimplemented from Nektar::StdRegions::StdExpansion3D.

Definition at line 487 of file TetExp.cpp.

References ASSERTL0, and Nektar::LocalRegions::Expansion::m_geom.

490  {
491  ASSERTL0(m_geom,"m_geom not defined");
492 
493  Array<OneD,NekDouble> Lcoord = Array<OneD,NekDouble>(3);
494 
495  // Get the local (eta) coordinates of the point
496  m_geom->GetLocCoords(coord,Lcoord);
497 
498  // Evaluate point in local (eta) coordinates.
499  return StdTetExp::v_PhysEvaluate(Lcoord,physvals);
500  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::LocalRegions::Expansion::m_geom
SpatialDomains::GeometrySharedPtr m_geom
Definition: Expansion.h:125
NekDouble Nektar::LocalRegions::TetExp::v_StdPhysEvaluate ( const Array< OneD, const NekDouble > &  Lcoord,
const Array< OneD, const NekDouble > &  physvals 
)
protectedvirtual

Given the local cartesian coordinate Lcoord evaluate the value of physvals at this point by calling through to the StdExpansion method

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 475 of file TetExp.cpp.

478  {
479  // Evaluate point in local (eta) coordinates.
480  return StdTetExp::v_PhysEvaluate(Lcoord,physvals);
481  }
void Nektar::LocalRegions::TetExp::v_SVVLaplacianFilter ( Array< OneD, NekDouble > &  array,
const StdRegions::StdMatrixKey &  mkey 
)
protectedvirtual

Reimplemented from Nektar::StdRegions::StdTetExp.

Definition at line 1008 of file TetExp.cpp.

References Nektar::SpatialDomains::eDeformed, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetTotPoints(), Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Vdiv(), Vmath::Vmul(), and Vmath::Vsqrt().

1011  {
1012  int nq = GetTotPoints();
1013 
1014  // Calculate sqrt of the Jacobian
1015  Array<OneD, const NekDouble> jac =
1016  m_metricinfo->GetJac(GetPointsKeys());
1017  Array<OneD, NekDouble> sqrt_jac(nq);
1018  if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
1019  {
1020  Vmath::Vsqrt(nq,jac,1,sqrt_jac,1);
1021  }
1022  else
1023  {
1024  Vmath::Fill(nq,sqrt(jac[0]),sqrt_jac,1);
1025  }
1026 
1027  // Multiply array by sqrt(Jac)
1028  Vmath::Vmul(nq,sqrt_jac,1,array,1,array,1);
1029 
1030  // Apply std region filter
1031  StdTetExp::v_SVVLaplacianFilter( array, mkey);
1032 
1033  // Divide by sqrt(Jac)
1034  Vmath::Vdiv(nq,array,1,sqrt_jac,1,array,1);
1035  }
Nektar::StdRegions::StdExpansion::GetPointsKeys
const LibUtilities::PointsKeyVector GetPointsKeys() const
Definition: StdExpansion.h:1276
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Nektar::LocalRegions::Expansion::m_metricinfo
SpatialDomains::GeomFactorsSharedPtr m_metricinfo
Definition: Expansion.h:126
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Nektar::StdRegions::StdExpansion::GetTotPoints
int GetTotPoints() const
This function returns the total number of quadrature points used in the element.
Definition: StdExpansion.h:141
Nektar::SpatialDomains::eDeformed
Geometry is curved or has non-constant factors.
Definition: SpatialDomains.hpp:57
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169

Member Data Documentation

LibUtilities::NekManager<MatrixKey, DNekScalMat, MatrixKey::opLess> Nektar::LocalRegions::TetExp::m_matrixManager
private

Definition at line 218 of file TetExp.h.

Referenced by CreateMatrix(), v_FwdTrans(), and v_GetLocMatrix().

LibUtilities::NekManager<MatrixKey, DNekScalBlkMat, MatrixKey::opLess> Nektar::LocalRegions::TetExp::m_staticCondMatrixManager
private

Definition at line 219 of file TetExp.h.

Referenced by v_DropLocStaticCondMatrix(), and v_GetLocStaticCondMatrix().

Generated on Tue Dec 8 2015 23:45:37 for Nektar++ by   doxygen 1.8.9.1