|
Nektar++
|
|
Nektar++
|
Specialisation of the NodalUtil class to support nodal hex elements. More...
#include <NodalUtil.h>

Public Member Functions | |
| NodalUtilHex (int degree, Array< OneD, NekDouble > r, Array< OneD, NekDouble > s, Array< OneD, NekDouble > t) | |
| Construct the nodal utility class for a hexahedron. More... | |
| virtual | ~NodalUtilHex () |
 Public Member Functions inherited from Nektar::LibUtilities::NodalUtil Public Member Functions inherited from Nektar::LibUtilities::NodalUtil | |
| NekVector< NekDouble > | GetWeights () |
| Obtain the integration weights for the given nodal distribution. More... | |
| SharedMatrix | GetVandermonde () |
| Return the Vandermonde matrix for the nodal distribution. More... | |
| SharedMatrix | GetVandermondeForDeriv (int dir) |
| Return the Vandermonde matrix of the derivative of the basis functions for the nodal distribution. More... | |
| SharedMatrix | GetDerivMatrix (int dir) |
| Return the derivative matrix for the nodal distribution. More... | |
| SharedMatrix | GetInterpolationMatrix (Array< OneD, Array< OneD, NekDouble > > &xi) |
Construct the interpolation matrix used to evaluate the basis at the points xi inside the element. More... | |
Protected Member Functions | |
| virtual NekVector< NekDouble > | v_OrthoBasis (const int mode) |
| Return the value of the modal functions for the hex element at the nodal points m_xi for a given mode. More... | |
| virtual NekVector< NekDouble > | v_OrthoBasisDeriv (const int dir, const int mode) |
| Return the values of the derivative of the orthogonal basis at the nodal points for a given mode. More... | |
| virtual boost::shared_ptr < NodalUtil > | v_CreateUtil (Array< OneD, Array< OneD, NekDouble > > &xi) |
| Construct a NodalUtil object of the appropriate element type for a given set of points. More... | |
| virtual NekDouble | v_ModeZeroIntegral () |
| Return the value of the integral of the zero-th mode for this element. More... | |
| virtual int | v_NumModes () |
| Calculate the number of degrees of freedom for this element. More... | |
 Protected Member Functions inherited from Nektar::LibUtilities::NodalUtil Protected Member Functions inherited from Nektar::LibUtilities::NodalUtil | |
| NodalUtil (int degree, int dim) | |
| Set up the NodalUtil object. More... | |
Protected Attributes | |
| std::vector< Mode > | m_ordering |
Mapping from the 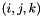 indexing of the basis to a continuous ordering. More... indexing of the basis to a continuous ordering. More... | |
 Protected Attributes inherited from Nektar::LibUtilities::NodalUtil Protected Attributes inherited from Nektar::LibUtilities::NodalUtil | |
| int | m_dim |
| Dimension of the nodal element. More... | |
| int | m_degree |
| Degree of the nodal element. More... | |
| int | m_numPoints |
| Total number of nodal points. More... | |
| Array< OneD, Array< OneD, NekDouble > > | m_xi |
| Coordinates of the nodal points defining the basis. More... | |
Private Types | |
| typedef boost::tuple< int, int, int > | Mode |
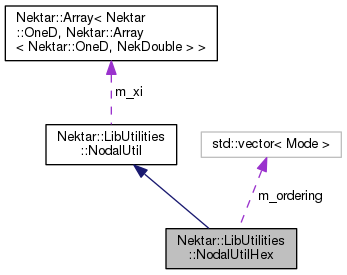
Specialisation of the NodalUtil class to support nodal hex elements.
Definition at line 353 of file NodalUtil.h.
|
private |
Definition at line 355 of file NodalUtil.h.
| Nektar::LibUtilities::NodalUtilHex::NodalUtilHex | ( | int | degree, |
| Array< OneD, NekDouble > | r, | ||
| Array< OneD, NekDouble > | s, | ||
| Array< OneD, NekDouble > | t | ||
| ) |
Construct the nodal utility class for a hexahedron.
The constructor of this class sets up the m_ordering member variable used in the evaluation of the orthogonal basis.
| degree | Polynomial order of this nodal hexahedron. |
| r | 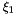 -coordinates of nodal points in the standard element. -coordinates of nodal points in the standard element. |
| s | 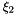 -coordinates of nodal points in the standard element. -coordinates of nodal points in the standard element. |
Definition at line 956 of file NodalUtil.cpp.
References Nektar::LibUtilities::NodalUtil::m_degree, Nektar::LibUtilities::NodalUtil::m_numPoints, m_ordering, and Nektar::LibUtilities::NodalUtil::m_xi.
|
inlinevirtual |
Definition at line 363 of file NodalUtil.h.
|
inlineprotectedvirtual |
Construct a NodalUtil object of the appropriate element type for a given set of points.
This function is used inside NodalUtil::GetInterpolationMatrix so that the (potentially non-square) Vandermonde matrix can be constructed to create the interpolation matrix at an arbitrary set of points in the domain.
| xi | Distribution of nodal points to create utility with. |
Implements Nektar::LibUtilities::NodalUtil.
Definition at line 376 of file NodalUtil.h.
References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::LibUtilities::NodalUtil::m_degree.
|
inlineprotectedvirtual |
Return the value of the integral of the zero-th mode for this element.
Note that for the orthogonal basis under consideration, all modes integrate to zero asides from the zero-th mode. This function is used in NodalUtil::GetWeights to determine integration weights.
Implements Nektar::LibUtilities::NodalUtil.
Definition at line 383 of file NodalUtil.h.
|
inlineprotectedvirtual |
Calculate the number of degrees of freedom for this element.
Implements Nektar::LibUtilities::NodalUtil.
Definition at line 388 of file NodalUtil.h.
References Nektar::LibUtilities::NodalUtil::m_degree.
|
protectedvirtual |
Return the value of the modal functions for the hex element at the nodal points m_xi for a given mode.
In a quad, we use the orthogonal basis
![\[ \psi_{m(ijk)} = P^{(0,0)}_i(\xi_1) P_j^{(0,0)}(\xi_2) P_k^{(0,0)}(\xi_3) \]](form_103.png)
| mode | The mode of the orthogonal basis to evaluate. |
Implements Nektar::LibUtilities::NodalUtil.
Definition at line 994 of file NodalUtil.cpp.
References Polylib::jacobfd(), Nektar::LibUtilities::NodalUtil::m_numPoints, m_ordering, Nektar::LibUtilities::NodalUtil::m_xi, and CG_Iterations::modes.
|
protectedvirtual |
Return the values of the derivative of the orthogonal basis at the nodal points for a given mode.
| dir | Coordinate direction of derivative. |
| mode | Mode number, which is between 0 and NodalUtil::v_NumModes()
|
Implements Nektar::LibUtilities::NodalUtil.
Definition at line 1020 of file NodalUtil.cpp.
References Polylib::jacobd(), Polylib::jacobfd(), Nektar::LibUtilities::NodalUtil::m_numPoints, m_ordering, Nektar::LibUtilities::NodalUtil::m_xi, and CG_Iterations::modes.
|
protected |
Mapping from the 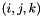 indexing of the basis to a continuous ordering.
indexing of the basis to a continuous ordering.
Definition at line 370 of file NodalUtil.h.
Referenced by NodalUtilHex(), v_OrthoBasis(), and v_OrthoBasisDeriv().
 1.8.8
1.8.8