|
Nektar++
|
|
Nektar++
|
Specialisation of the NodalUtil class to support nodal triangular elements. More...
#include <NodalUtil.h>
Public Member Functions | |
| NodalUtilTriangle (int degree, Array< OneD, NekDouble > r, Array< OneD, NekDouble > s) | |
| Construct the nodal utility class for a triangle. More... | |
| virtual | ~NodalUtilTriangle () |
 Public Member Functions inherited from Nektar::LibUtilities::NodalUtil Public Member Functions inherited from Nektar::LibUtilities::NodalUtil | |
| NekVector< NekDouble > | GetWeights () |
| Obtain the integration weights for the given nodal distribution. More... | |
| SharedMatrix | GetVandermonde () |
| Return the Vandermonde matrix for the nodal distribution. More... | |
| SharedMatrix | GetVandermondeForDeriv (int dir) |
| Return the Vandermonde matrix of the derivative of the basis functions for the nodal distribution. More... | |
| SharedMatrix | GetDerivMatrix (int dir) |
| Return the derivative matrix for the nodal distribution. More... | |
| SharedMatrix | GetInterpolationMatrix (Array< OneD, Array< OneD, NekDouble > > &xi) |
Construct the interpolation matrix used to evaluate the basis at the points xi inside the element. More... | |
Protected Member Functions | |
| virtual NekVector< NekDouble > | v_OrthoBasis (const int mode) |
| Return the value of the modal functions for the triangular element at the nodal points m_xi for a given mode. More... | |
| virtual NekVector< NekDouble > | v_OrthoBasisDeriv (const int dir, const int mode) |
| Return the value of the derivative of the modal functions for the triangular element at the nodal points m_xi for a given mode. More... | |
| virtual boost::shared_ptr < NodalUtil > | v_CreateUtil (Array< OneD, Array< OneD, NekDouble > > &xi) |
| Construct a NodalUtil object of the appropriate element type for a given set of points. More... | |
| virtual NekDouble | v_ModeZeroIntegral () |
| Return the value of the integral of the zero-th mode for this element. More... | |
| virtual int | v_NumModes () |
| Calculate the number of degrees of freedom for this element. More... | |
 Protected Member Functions inherited from Nektar::LibUtilities::NodalUtil Protected Member Functions inherited from Nektar::LibUtilities::NodalUtil | |
| NodalUtil (int degree, int dim) | |
| Set up the NodalUtil object. More... | |
Protected Attributes | |
| std::vector< std::pair< int, int > > | m_ordering |
Mapping from the 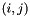 indexing of the basis to a continuous ordering. More... indexing of the basis to a continuous ordering. More... | |
| Array< OneD, Array< OneD, NekDouble > > | m_eta |
Collapsed coordinates 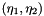 of the nodal points. More... of the nodal points. More... | |
 Protected Attributes inherited from Nektar::LibUtilities::NodalUtil Protected Attributes inherited from Nektar::LibUtilities::NodalUtil | |
| int | m_dim |
| Dimension of the nodal element. More... | |
| int | m_degree |
| Degree of the nodal element. More... | |
| int | m_numPoints |
| Total number of nodal points. More... | |
| Array< OneD, Array< OneD, NekDouble > > | m_xi |
| Coordinates of the nodal points defining the basis. More... | |
Specialisation of the NodalUtil class to support nodal triangular elements.
Definition at line 170 of file NodalUtil.h.
| Nektar::LibUtilities::NodalUtilTriangle::NodalUtilTriangle | ( | int | degree, |
| Array< OneD, NekDouble > | r, | ||
| Array< OneD, NekDouble > | s | ||
| ) |
Construct the nodal utility class for a triangle.
The constructor of this class sets up two member variables used in the evaluation of the orthogonal basis:
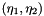 inside the square
inside the square ![$[-1,1]^2$](form_80.png) on which the orthogonal basis functions are defined.
on which the orthogonal basis functions are defined.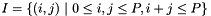 to an ordering
to an ordering 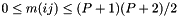 that defines the monomials
that defines the monomials 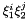 that span the triangular space. This is then used to calculate which
that span the triangular space. This is then used to calculate which 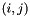 pair corresponding to a column of the Vandermonde matrix when calculating the orthogonal polynomials.
pair corresponding to a column of the Vandermonde matrix when calculating the orthogonal polynomials.| degree | Polynomial order of this nodal triangle. |
| r | 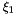 -coordinates of nodal points in the standard element. -coordinates of nodal points in the standard element. |
| s | 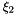 -coordinates of nodal points in the standard element. -coordinates of nodal points in the standard element. |
Definition at line 239 of file NodalUtil.cpp.
References Nektar::NekConstants::kNekZeroTol, Nektar::LibUtilities::NodalUtil::m_degree, m_eta, Nektar::LibUtilities::NodalUtil::m_numPoints, m_ordering, and Nektar::LibUtilities::NodalUtil::m_xi.
|
inlinevirtual |
Definition at line 177 of file NodalUtil.h.
|
inlineprotectedvirtual |
Construct a NodalUtil object of the appropriate element type for a given set of points.
This function is used inside NodalUtil::GetInterpolationMatrix so that the (potentially non-square) Vandermonde matrix can be constructed to create the interpolation matrix at an arbitrary set of points in the domain.
| xi | Distribution of nodal points to create utility with. |
Implements Nektar::LibUtilities::NodalUtil.
Reimplemented in Nektar::Utilities::NodalUtilTriMonomial.
Definition at line 193 of file NodalUtil.h.
References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::LibUtilities::NodalUtil::m_degree.
|
inlineprotectedvirtual |
Return the value of the integral of the zero-th mode for this element.
Note that for the orthogonal basis under consideration, all modes integrate to zero asides from the zero-th mode. This function is used in NodalUtil::GetWeights to determine integration weights.
Implements Nektar::LibUtilities::NodalUtil.
Definition at line 200 of file NodalUtil.h.
|
inlineprotectedvirtual |
Calculate the number of degrees of freedom for this element.
Implements Nektar::LibUtilities::NodalUtil.
Definition at line 205 of file NodalUtil.h.
References Nektar::LibUtilities::NodalUtil::m_degree.
|
protectedvirtual |
Return the value of the modal functions for the triangular element at the nodal points m_xi for a given mode.
In a triangle, we use the orthogonal basis
![\[ \psi_{m(ij)} = \sqrt{2} P^{(0,0)}_i(\xi_1) P_j^{(2i+1,0)}(\xi_2) (1-\xi_2)^i \]](form_87.png)
where 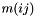 is the mapping defined in NodalUtilTriangle::m_ordering and
is the mapping defined in NodalUtilTriangle::m_ordering and 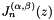 denotes the standard Jacobi polynomial.
denotes the standard Jacobi polynomial.
| mode | The mode of the orthogonal basis to evaluate. |
Implements Nektar::LibUtilities::NodalUtil.
Reimplemented in Nektar::Utilities::NodalUtilTriMonomial.
Definition at line 295 of file NodalUtil.cpp.
References Polylib::jacobfd(), m_eta, Nektar::LibUtilities::NodalUtil::m_numPoints, m_ordering, and CG_Iterations::modes.
|
protectedvirtual |
Return the value of the derivative of the modal functions for the triangular element at the nodal points m_xi for a given mode.
Note that this routine must use the chain rule combined with the collapsed coordinate derivatives as described in Sherwin & Karniadakis (2nd edition), pg 150.
| dir | Coordinate direction in which to evaluate the derivative. |
| mode | The mode of the orthogonal basis to evaluate. |
Implements Nektar::LibUtilities::NodalUtil.
Reimplemented in Nektar::Utilities::NodalUtilTriMonomial.
Definition at line 333 of file NodalUtil.cpp.
References Polylib::jacobd(), Polylib::jacobfd(), m_eta, Nektar::LibUtilities::NodalUtil::m_numPoints, m_ordering, and CG_Iterations::modes.
Collapsed coordinates 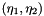 of the nodal points.
of the nodal points.
Definition at line 187 of file NodalUtil.h.
Referenced by NodalUtilTriangle(), v_OrthoBasis(), and v_OrthoBasisDeriv().
|
protected |
Mapping from the 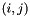 indexing of the basis to a continuous ordering.
indexing of the basis to a continuous ordering.
Definition at line 184 of file NodalUtil.h.
Referenced by NodalUtilTriangle(), v_OrthoBasis(), Nektar::Utilities::NodalUtilTriMonomial::v_OrthoBasis(), and v_OrthoBasisDeriv().
 1.8.8
1.8.8