|
Nektar++
|
|
Nektar++
|
Classes | |
| struct | cmpop |
| struct | DerivUtil |
| struct | EdgeInfo |
| struct | ElmtConfigHash |
| class | ElUtil |
| class | ElUtilJob |
| class | InputGmsh |
| class | InputMCF |
| class | InputNek |
| class | InputNek5000 |
| class | InputNekpp |
| class | InputPly |
| Converter for Ply files. More... | |
| class | InputSem |
| class | InputStar |
| Converter for VTK files. More... | |
| class | InputSwan |
| Converter for Swansea mesh format. More... | |
| class | InputTec |
| Converter for VTK files. More... | |
| class | InputVtk |
| Converter for VTK files. More... | |
| class | NodalUtilTriMonomial |
| struct | NodeComparator |
| class | NodeOpti |
| class | NodeOpti1D3D |
| class | NodeOpti2D2D |
| class | NodeOpti2D3D |
| class | NodeOpti3D3D |
| class | NodeOptiJob |
| class | OutputGmsh |
| Converter for Gmsh files. More... | |
| class | OutputNekpp |
| Converter for Gmsh files. More... | |
| class | OutputSTL |
| class | OutputVtk |
| Converter for Gmsh files. More... | |
| class | ProcessBL |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessCurve |
| class | ProcessCurvedEdges |
| class | ProcessCyl |
| class | ProcessDetectSurf |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessExtractSurf |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessExtractTetPrismInterface |
| Module to extract interface between prismatic and tetrahedral elements. More... | |
| class | ProcessExtrude |
| This processing module extrudes a 2d mesh in the z direction. More... | |
| class | ProcessInsertSurface |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessJac |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessLinear |
| This processing module removes all the high-order information from the mesh leaving just the linear elements. More... | |
| class | ProcessLinkCheck |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessOptiExtract |
| class | ProcessPerAlign |
| class | ProcessScalar |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessSpherigon |
| class | ProcessTetSplit |
| This processing module calculates the Jacobian of elements using SpatialDomains::GeomFactors and the Element::GetGeom method. For now it simply prints a list of elements which have negative Jacobian. More... | |
| class | ProcessVarOpti |
| struct | Residual |
| struct | SplitEdgeHelper |
| struct | SplitMapHelper |
Typedefs | |
| typedef boost::tuple< int, int, int > | Mode |
| typedef boost::shared_ptr < InputPly > | InputPlySharedPtr |
| typedef std::pair< int, int > | ipair |
| typedef boost::shared_ptr < DerivUtil > | DerivUtilSharedPtr |
| typedef boost::shared_ptr < Residual > | ResidualSharedPtr |
| typedef boost::shared_ptr< ElUtil > | ElUtilSharedPtr |
| typedef boost::shared_ptr < NodeOpti > | NodeOptiSharedPtr |
| typedef LibUtilities::NekFactory< int, NodeOpti, NodeSharedPtr, std::vector< ElUtilSharedPtr > , ResidualSharedPtr, std::map < LibUtilities::ShapeType, DerivUtilSharedPtr >, optiType > | NodeOptiFactory |
Enumerations | |
| enum | NekCurve { eFile, eRecon } |
| enum | optiType { eLinEl, eWins, eRoca, eHypEl } |
Functions | |
| std::vector< int > | quadTensorNodeOrdering (const std::vector< int > &nodes, int n) |
| Reorder Gmsh nodes so that they appear in a tensor product format suitable for the interior of a Nektar++ quadrilateral. More... | |
| std::vector< int > | triTensorNodeOrdering (const std::vector< int > &nodes, int n) |
| Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ triangle. More... | |
| std::vector< int > | tetTensorNodeOrdering (const std::vector< int > &nodes, int n) |
| Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ tetrahedron. More... | |
| std::vector< int > | prismTensorNodeOrdering (const std::vector< int > &nodes, int n) |
| Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ prism. This routine is specifically designed for interior Gmsh nodes only. More... | |
| std::vector< int > | hexTensorNodeOrdering (const std::vector< int > &nodes, int n) |
| Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ hexahedron. More... | |
| static void | PrismLineFaces (int prismid, map< int, int > &facelist, vector< vector< int > > &FacesToPrisms, vector< vector< int > > &PrismsToFaces, vector< bool > &PrismDone) |
| static void | PrismLineFaces (int prismid, map< int, int > &facelist, vector< vector< int > > &FacesToPrisms, vector< vector< int > > &PrismsToFaces, vector< bool > &PrismDone) |
| bool | operator== (NekMeshUtils::ElmtConfig const &p1, NekMeshUtils::ElmtConfig const &p2) |
| template<typename T > | |
| void | TestElmts (SpatialDomains::MeshGraphSharedPtr &graph) |
| int ** | helper2d (int lda, int arr[][2]) |
| int ** | helper2d (int lda, int arr[][4]) |
| template<int DIM> | |
| NekDouble | Determinant (NekDouble jac[][DIM]) |
| Calculate determinant of input matrix. More... | |
| template<> | |
| NekDouble | Determinant< 2 > (NekDouble jac[][2]) |
| template<> | |
| NekDouble | Determinant< 3 > (NekDouble jac[][3]) |
| template<int DIM> | |
| void | InvTrans (NekDouble in[][DIM], NekDouble out[][DIM]) |
| Calculate inverse transpose of input matrix. More... | |
| template<> | |
| void | InvTrans< 2 > (NekDouble in[][2], NekDouble out[][2]) |
| template<> | |
| void | InvTrans< 3 > (NekDouble in[][3], NekDouble out[][3]) |
| template<int DIM> | |
| NekDouble | ScalarProd (NekDouble(&in1)[DIM], NekDouble(&in2)[DIM]) |
| Calculate Scalar product of input vectors. More... | |
| template<> | |
| NekDouble | ScalarProd< 2 > (NekDouble(&in1)[2], NekDouble(&in2)[2]) |
| template<> | |
| NekDouble | ScalarProd< 3 > (NekDouble(&in1)[3], NekDouble(&in2)[3]) |
| template<int DIM> | |
| void | EMatrix (NekDouble in[][DIM], NekDouble out[][DIM]) |
Calculate 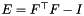 tensor used in derivation of linear elasticity gradients. More... tensor used in derivation of linear elasticity gradients. More... | |
| template<> | |
| void | EMatrix< 2 > (NekDouble in[][2], NekDouble out[][2]) |
| template<> | |
| void | EMatrix< 3 > (NekDouble in[][3], NekDouble out[][3]) |
| template<int DIM> | |
| NekDouble | FrobProd (NekDouble in1[][DIM], NekDouble in2[][DIM]) |
| Calculate Frobenius inner product of input matrices. More... | |
| template<> | |
| NekDouble | FrobProd< 2 > (NekDouble in1[][2], NekDouble in2[][2]) |
| template<> | |
| NekDouble | FrobProd< 3 > (NekDouble in1[][3], NekDouble in2[][3]) |
| template<int DIM> | |
| NekDouble | FrobeniusNorm (NekDouble inarray[][DIM]) |
Calculate Frobenius norm 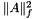 of a matrix of a matrix 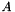 . More... . More... | |
| template<> | |
| NekDouble | FrobeniusNorm< 2 > (NekDouble inarray[][2]) |
| template<> | |
| NekDouble | FrobeniusNorm< 3 > (NekDouble inarray[][3]) |
| NodeOptiFactory & | GetNodeOptiFactory () |
Variables | |
| boost::mutex | mtx2 |
| boost::mutex | mtx |
| typedef boost::shared_ptr< DerivUtil > Nektar::Utilities::DerivUtilSharedPtr |
| typedef boost::shared_ptr<ElUtil> Nektar::Utilities::ElUtilSharedPtr |
| typedef boost::shared_ptr<InputPly> Nektar::Utilities::InputPlySharedPtr |
Definition at line 68 of file InputPly.h.
| typedef std::pair<int, int> Nektar::Utilities::ipair |
Definition at line 55 of file ProcessTetSplit.cpp.
| typedef boost::tuple<int, int, int> Nektar::Utilities::Mode |
Definition at line 221 of file InputGmsh.cpp.
| typedef LibUtilities::NekFactory< int, NodeOpti, NodeSharedPtr, std::vector<ElUtilSharedPtr>, ResidualSharedPtr, std::map<LibUtilities::ShapeType, DerivUtilSharedPtr>, optiType> Nektar::Utilities::NodeOptiFactory |
Definition at line 140 of file NodeOpti.h.
| typedef boost::shared_ptr<NodeOpti> Nektar::Utilities::NodeOptiSharedPtr |
Definition at line 135 of file NodeOpti.h.
| typedef boost::shared_ptr< Residual > Nektar::Utilities::ResidualSharedPtr |
| Enumerator | |
|---|---|
| eFile | |
| eRecon | |
Definition at line 51 of file InputNek.h.
| Enumerator | |
|---|---|
| eLinEl | |
| eWins | |
| eRoca | |
| eHypEl | |
Definition at line 61 of file ProcessVarOpti.h.
|
inline |
Calculate determinant of input matrix.
Specialised versions of this function exist only for 2x2 and 3x3 matrices.
| jac | Input matrix |
jac. Definition at line 55 of file Evaluator.hxx.
Referenced by Nektar::Utilities::NodeOpti::GetFunctional().
|
inline |
Definition at line 60 of file Evaluator.hxx.
Referenced by InvTrans< 2 >().
|
inline |
Definition at line 65 of file Evaluator.hxx.
Referenced by InvTrans< 3 >(), and Nektar::Utilities::NodeOpti::MinEigen().
|
inline |
Calculate 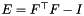 tensor used in derivation of linear elasticity gradients.
tensor used in derivation of linear elasticity gradients.
Specialised versions of this function exist only for 2x2 and 3x3 matrices.
| in | Input matrix 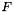 |
| out | Output matrix 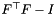 |
Definition at line 162 of file Evaluator.hxx.
|
inline |
Definition at line 166 of file Evaluator.hxx.
|
inline |
Definition at line 174 of file Evaluator.hxx.
|
inline |
Calculate Frobenius norm 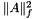 of a matrix
of a matrix 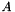 .
.
| inarray | Input matrix 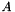 |
Definition at line 234 of file Evaluator.hxx.
Referenced by Nektar::Utilities::NodeOpti::GetFunctional().
|
inline |
Definition at line 240 of file Evaluator.hxx.
|
inline |
Definition at line 249 of file Evaluator.hxx.
|
inline |
Calculate Frobenius inner product of input matrices.
Definition at line 199 of file Evaluator.hxx.
|
inline |
Definition at line 206 of file Evaluator.hxx.
|
inline |
Definition at line 215 of file Evaluator.hxx.
| NodeOptiFactory & Nektar::Utilities::GetNodeOptiFactory | ( | ) |
Definition at line 52 of file NodeOpti.cpp.
Referenced by Nektar::Utilities::ProcessVarOpti::Analytics(), and Nektar::Utilities::ProcessVarOpti::Process().
| int** Nektar::Utilities::helper2d | ( | int | lda, |
| int | arr[][2] | ||
| ) |
Definition at line 62 of file ProcessBL.cpp.
Referenced by Nektar::Utilities::ProcessBL::BoundaryLayer3D().
| int** Nektar::Utilities::helper2d | ( | int | lda, |
| int | arr[][4] | ||
| ) |
Definition at line 74 of file ProcessBL.cpp.
| std::vector<int> Nektar::Utilities::hexTensorNodeOrdering | ( | const std::vector< int > & | nodes, |
| int | n | ||
| ) |
Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ hexahedron.
For an example, consider a second order hexahedron. This routine will produce a permutation map that applies the following permutation:
``` 3-—13-—2 6-—7--—8 |\ |\ |\ |\ |15 24 | 14 |15 16 | 18 9 \ 20 11 \ 3 \ 4 5 \ | 7-—19+—6 | 24—25+—26 |22 | 26 | 23| |12 | 13 | 14| 0—+-8-—1 | 0—+-1-—2 | \ 17 25 \ 18 \ 21 22 \ 23 10 | 21 12| 9 | 10 11| | | | | 4-—16-—5 18—19-—20
Gmsh tensor-product ```
We assume that Gmsh uses a recursive ordering system, so that interior nodes are reordered by calling this function recursively.
| nodes | The integer IDs of the nodes to be reordered, in Gmsh format. |
| n | The number of nodes in one coordinate direction. If this is zero we assume no reordering needs to be done and return the identity permutation. |
Definition at line 540 of file InputGmsh.cpp.
References Nektar::StdRegions::eDir1BwdDir1_Dir2FwdDir2, Nektar::StdRegions::eDir1FwdDir1_Dir2FwdDir2, Nektar::StdRegions::eDir1FwdDir2_Dir2FwdDir1, and quadTensorNodeOrdering().
Referenced by Nektar::Utilities::InputGmsh::HexReordering().
|
inline |
Calculate inverse transpose of input matrix.
Specialised versions of this function exist only for 2x2 and 3x3 matrices.
| in | Input matrix 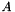 |
| out | Output matrix 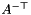 |
Definition at line 81 of file Evaluator.hxx.
|
inline |
Definition at line 85 of file Evaluator.hxx.
References Determinant< 2 >().
|
inline |
Definition at line 95 of file Evaluator.hxx.
References Determinant< 3 >().
| bool Nektar::Utilities::operator== | ( | NekMeshUtils::ElmtConfig const & | p1, |
| NekMeshUtils::ElmtConfig const & | p2 | ||
| ) |
Definition at line 61 of file OutputGmsh.h.
References Nektar::NekMeshUtils::ElmtConfig::m_e, Nektar::NekMeshUtils::ElmtConfig::m_faceNodes, Nektar::NekMeshUtils::ElmtConfig::m_order, and Nektar::NekMeshUtils::ElmtConfig::m_volumeNodes.
|
static |
Definition at line 422 of file InputStar.cpp.
Referenced by PrismLineFaces(), Nektar::Utilities::InputStar::ResetNodes(), and Nektar::Utilities::InputTec::ResetNodes().
|
static |
Definition at line 636 of file InputStarTec.cpp.
References PrismLineFaces().
| std::vector<int> Nektar::Utilities::prismTensorNodeOrdering | ( | const std::vector< int > & | nodes, |
| int | n | ||
| ) |
Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ prism. This routine is specifically designed for interior Gmsh nodes only.
Prisms are a bit of a special case, in that interior nodes are heterogeneous in the number of points they use. As an example, for a second-order interior of a fourth-order prism, this routine calculates the mapping taking us
``` ,6 ,8 .-' | \ .-' | \ ,-3 | \ ,-5 | \ ,-' | \ | \ ,-' | \ | \ 2 | \7----—8 2 | \6----—7 | \ | ,-' \ ,-' | \ | ,-' \ ,-' | \,5---—,0' | \,3---—,4' |,-' \ ,-' |,-' \ ,-' 1----—4' 0----—1'
Gmsh tensor-product
```
| nodes | The integer IDs of the nodes to be reordered, in Gmsh format. |
| n | The number of nodes in one coordinate direction. If this is zero we assume no reordering needs to be done and return the identity permutation. |
Definition at line 464 of file InputGmsh.cpp.
References ASSERTL0.
Referenced by Nektar::Utilities::InputGmsh::PrismReordering().
| std::vector<int> Nektar::Utilities::quadTensorNodeOrdering | ( | const std::vector< int > & | nodes, |
| int | n | ||
| ) |
Reorder Gmsh nodes so that they appear in a tensor product format suitable for the interior of a Nektar++ quadrilateral.
For an example, consider a second order quadrilateral. This routine will produce a permutation map that applies the following permutation:
``` 3—6—2 6—7—8 | | | | 7 8 5 —> 3 4 5 | | | | 0—4—1 0—1—2
Gmsh tensor-product ```
We assume that Gmsh uses a recursive ordering system, so that interior nodes are reordered by calling this function recursively.
| nodes | The integer IDs of the nodes to be reordered, in Gmsh format. |
| n | The number of nodes in one coordinate direction. If this is zero we assume no reordering needs to be done and return the identity permutation. |
Definition at line 93 of file InputGmsh.cpp.
References CellMLToNektar.pycml::copy().
Referenced by Nektar::Utilities::InputGmsh::HexReordering(), hexTensorNodeOrdering(), Nektar::Utilities::InputGmsh::PrismReordering(), and Nektar::Utilities::InputGmsh::QuadReordering().
|
inline |
Calculate Scalar product of input vectors.
Definition at line 132 of file Evaluator.hxx.
|
inline |
Definition at line 138 of file Evaluator.hxx.
|
inline |
Definition at line 144 of file Evaluator.hxx.
| void Nektar::Utilities::TestElmts | ( | SpatialDomains::MeshGraphSharedPtr & | graph | ) |
Definition at line 79 of file OutputNekpp.cpp.
| std::vector<int> Nektar::Utilities::tetTensorNodeOrdering | ( | const std::vector< int > & | nodes, |
| int | n | ||
| ) |
Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ tetrahedron.
For an example, consider a second order tetrahedron. This routine will produce a permutation map that applies the following permutation:
``` 2 5 ,/|\ ,/|\ ,/ | \ ,/ |\ ,6 '. `5 ,3 '. 4 ,/ 8\ ,/ 8 \ ,/ |\ ,/ | `\ 0-----—4–'.-----—1 0-----—1–'.-----—2 \. | ,/. | ,/ \. | ,9. | ,7 `7. '. ,/ `6. '. ,/ \. |/. |/ 39
Gmsh tensor-product ```
We assume that Gmsh uses a recursive ordering system, so that interior nodes are reordered by calling this function recursively.
| nodes | The integer IDs of the nodes to be reordered, in Gmsh format. |
| n | The number of nodes in one coordinate direction. If this is zero we assume no reordering needs to be done and return the identity permutation. |
Definition at line 285 of file InputGmsh.cpp.
References Nektar::NekMeshUtils::HOTriangle< T >::Align(), Nektar::NekMeshUtils::HOTriangle< T >::surfVerts, and triTensorNodeOrdering().
Referenced by Nektar::Utilities::InputGmsh::TetReordering().
| std::vector<int> Nektar::Utilities::triTensorNodeOrdering | ( | const std::vector< int > & | nodes, |
| int | n | ||
| ) |
Reorder Gmsh nodes so that they appear in a "tensor product" format suitable for the interior of a Nektar++ triangle.
For an example, consider a third-order triangle. This routine will produce a permutation map that applies the following permutation:
``` 2 9 | \ | \ 7 6 7 7 | \ | \ 8 9 5 4 5 6 | \ | \ 0—3—4—1 0—1—2—3
Gmsh tensor-product
```
We assume that Gmsh uses a recursive ordering system, so that interior nodes are reordered by calling this function recursively.
| nodes | The integer IDs of the nodes to be reordered, in Gmsh format. |
| n | The number of nodes in one coordinate direction. If this is zero we assume no reordering needs to be done and return the identity permutation. |
Definition at line 170 of file InputGmsh.cpp.
References CellMLToNektar.pycml::copy().
Referenced by Nektar::Utilities::InputGmsh::PrismReordering(), Nektar::Utilities::InputGmsh::TetReordering(), tetTensorNodeOrdering(), and Nektar::Utilities::InputGmsh::TriReordering().
| boost::mutex Nektar::Utilities::mtx |
Definition at line 47 of file NodeOptiCAD.cpp.
Referenced by Nektar::Utilities::NodeOpti3D3D::Optimise(), and Nektar::Utilities::NodeOpti2D2D::Optimise().
| boost::mutex Nektar::Utilities::mtx2 |
Definition at line 48 of file ElUtil.cpp.
 1.8.8
1.8.8