1 Introduction

Chapter 1
Introduction

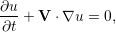
Welcome to the tutorial of the Advection problem using the Advection-Diffusion-Reaction (ADR) Solver in the Nektar++ framework. This tutorial is aimed to show the main features of the ADR solver in a simple manner. If you have not already downloaded and installed Nektar++, please do so by visiting nektar.info, where you can also find the User-Guide with the instructions to install the library.

This tutorial requires:

Nektar++ ADRSolver and pre- and post-processing tools,
the open-source mesh generator Gmsh,
the visualisation tool Paraview or VisIt

1.1 Goals

After the completion of this tutorial, you will be familiar with:

the generation of a simple mesh in Gmsh and its conversion into a Nektar++-compatible format;
the visualisation of the mesh in Paraview or VisIt
the setup of the initial and boundary conditions, the parameters and the solver settings;
running a simulation with the ADR solver; and
the post-processing of the data and the visualisation of the results in Paraview or VisIt.

Task: 1.1 Prepare for the tutorial. Make sure that you have:

Installed and tested Nektar++ v4.3.5from a binary package, or compiled it from source. By default binary packages will install all executables in /usr/bin. If you compile from source they will be in the sub-directory dist/bin of the build directory you created in the Nektar++ source tree. We will refer to the directory containing the executables as $NEK for the remainder of the tutorial.
Downloaded the tutorial files: basics-advection-diffusion.tar.gz
Unpack it using tar -xzvf basics-advection-diffusion.tar.gz to produce a directory basics-advection-diffusion with subdirectories called tutorial and complete.
We will refer to the tutorial directory as $NEKTUTORIAL.

The tutorial folder contains:
- a Gmsh file to generate the mesh, ADR_mesh.geo;
- a .msh file containing the mesh in Gmsh format, ADR_mesh.msh;

Task: 1.2 Additionally, you should also install

a visualization package capable of reading VTK files, such as ParaView (which can be downloaded from here) or VisIt (downloaded from here). Alternatively, you can generate Tecplot formatted .dat files for use with Tecplot.

1.2 Background

The ADR solver can solve various problems, including the unsteady advection, unsteady diffusion, unsteady advection diffusion equation, etc. For a more detailed description of this solver, please refer to the User-Guide.

In this tutorial we focus on the unsteady advection equation

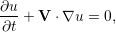∂u ∂t-+ V ⋅∇u = 0,

(1.1)

where u is the independent variable and V = [V_xV_yV_z] is the advection velocity. The unsteady advection equation can be solved in one, two and three spatial dimensions. We will here consider a two-dimensional problem, so that V = [V_xV_y].

1.3 Problem description

The problem we want to run consists of a given initial condition (which depends on x and y) travelling in the x-direction at a constant advection velocity. To model this problem we create a computational domain also referred to as mesh or grid (see section 2.1) on which we apply the following two-dimensional function as initial condition and periodic as well as time-dependent Dirichlet boundary conditions at the mesh boundaries

∂u ∂u ∂u ∂t-+ Vx ∂x-+ Vy ∂y-= 0, u(x,y;t = 0) = sin(κx )cos(κy ), u(xb = [− 1,1],yb;t) = periodic, u(xb,yb = [− 1,1];t) = sin(κ(x− Vxt )) cos(κ(y − Vyt)),

(1.2)

where x_b and y_b represent the boundaries of the computational domain (see section 2.2), V_x = 2,V_y = 0 and κ = 2π.

We successively setup the other parameters of the problem, such as the time-step, the time-integration scheme, the I/O configuration, etc. (see section 2.2). We finally run the solver (see section 3) and post-process the data in order to visualise the results (see section 4).

[next] [prev] [prev-tail] [front] [up]

Chapter 1Introduction

1.1 Goals

1.2 Background

1.3 Problem description

Chapter 1
Introduction