Chapter 2
Pre-processing

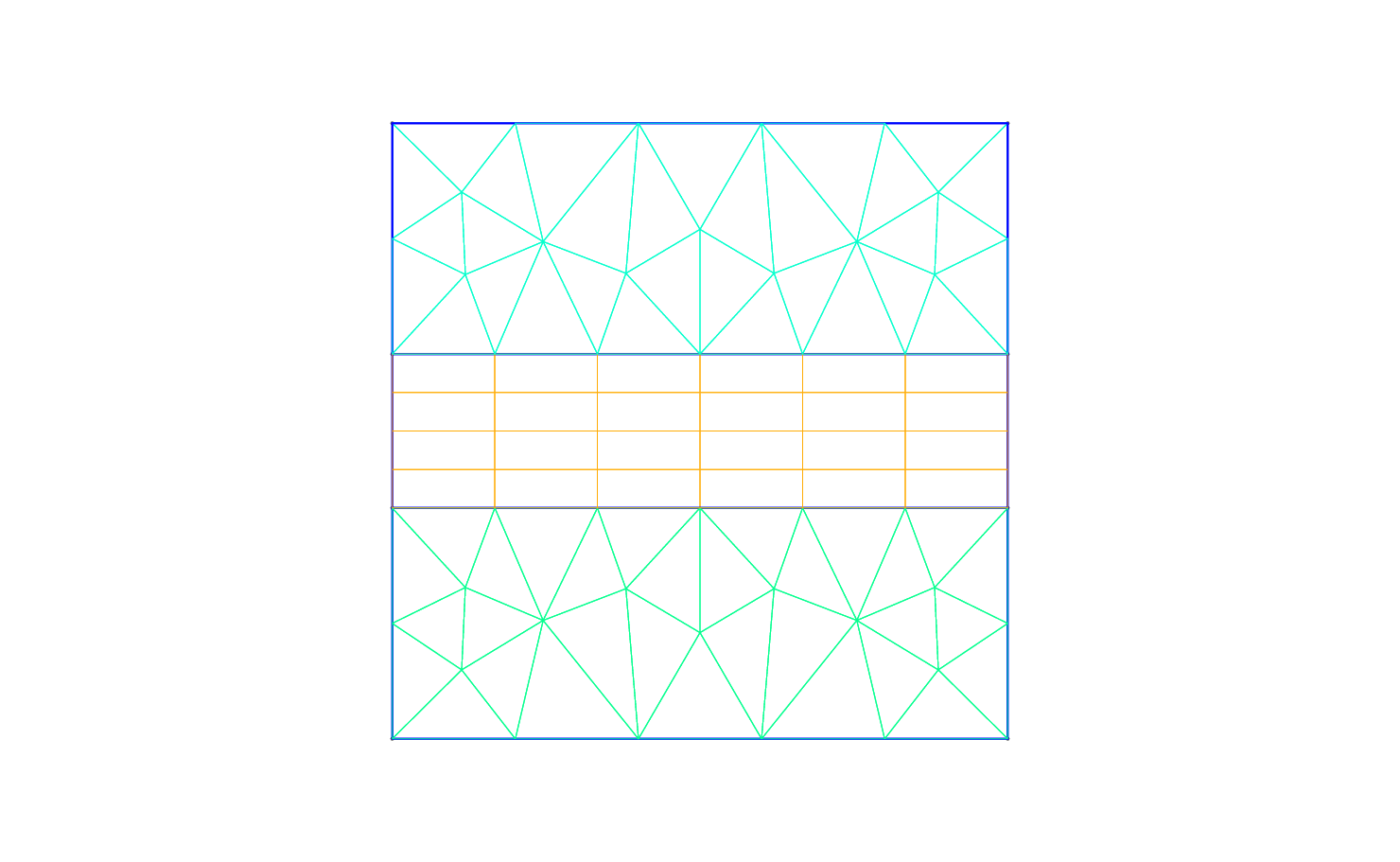
As already mentioned to set up the probelm we have two step. The first is setting up a mesh in an input xml format consistent with Nektar++ as discussed in section 2.1. We also need to configure the problem initial, boundary and parameters which are discussed in 2.2.

2.1 Mesh generation

The first pre-processing step consists in generating the mesh in a Nektar++ compatible format. One option to do this is to use the open-source mesh-generator Gmsh to first create the geometry, that in our case is a square and successively the mesh. The mesh format provided by Gmsh shown in Fig. (2.1) - i.e. .msh extension - is not consistent with the Nektar++ solvers and, therefore, it needs to be converted.

To do so, we need to run the pre-processing routine called NekMesh within Nektar++. This routine requires two line arguments, the mesh file generated by Gmsh, ADR_mesh.msh, and the name of the Nektar++-compatible mesh file that NekMesh will generate, for instance ADR_mesh.xml. The command line for this step is

After having generated the mesh file in a Nektar++-compatible format, ADR_mesh.xml, we can visualise the mesh. This step can be done by using the following Nektar++ built-in post-processing routine:

Before configuring the input files, if we want to use periodic boundary conditions, we need to make sure that the edges of the two periodic boundaries (i.e. x_b = [−1,1],y_b) are properly aligned. Gmsh and the NekMesh routine within Nektar++ does not guarantee proper alignment. However, NekMesh provides a module, called peralign, that enforces the reordering of pair of edges (for more details refer to the User-Guide. We can apply this by using the following command:

After having typed the last command, we have a mesh, ADR_mesh_aligned.xml, which is fully compatible with Nektar++ and which allows us applying periodic boundary conditions without encountering errors.

We can therefore now configure the conditions: initial conditions, boundary conditions, parameters and solver settings.

2.2 Configuring problem definitions

To set the various problem parameters, the solver settings, initial and boundary conditions and the expansion basese, we create a new file called ADR_conditions.xml, which can be found within the completed directory for this tutorial. This new file contains the CONDITIONS tag where we can specify the parameters of the simulations, the solver settings, the initial conditions, the boundary conditions and the exact solution and contains the EXPANSIONS tag where we can specify the polynomial order to be used inside each element of the mesh, the type of expansion bases and the type of points.

We begin to describe the ADR_conditions.xml file from the CONDITIONS tag, and in particular from the boundary conditions, initial conditions and exact solution sections:

In the above piece of .xml, we first need to specify the non-optional tag called VARIABLES that sets the solution variable (in this case u).

The second tag that needs to be specified is BOUNDARYREGIONS through which the user can specify the regions where to apply the boundary conditions. For instance, <B ID="0"> C[100] </B> indicates that composite 100 (which has been introduced in section 2.1) has a boundary ID equal to 0. This boundary ID is successively used to prescribe the boundary conditions.

The third tag is BOUNDARYCONDITIONS by which the boundary conditions are actually specified for each boundary ID specified in the BOUNDARYREGIONS tag. The syntax <D VAR="u" corresponds to a Dirichlet boundary condition for the variable u (note that in this case we used the additional tag USERDEFINEDTYPE="TimeDependent" which is a special option when using time-dependent boundary conditions), while <P VAR="u" corresponds to Periodic boundary conditions. For additional details on the various options possible in terms of boundary conditions refer to the User-Guide.

Finally, <FUNCTION NAME="InitialConditions"> allows the specification of the initial conditions, <FUNCTION NAME="AdvectionVelocity"> specifies the advection velocities in both the x- and y-direction (for this two-dimensional case) and is a non-optional parameters for the unsteady advection equation and <FUNCTION NAME="ExactSolution"> permits us to provide the exact solution, against which the L₂ and L_∞ errors are computed.

After having configured the VARIABLES tag, the initial and boundary conditions, the advection velocity and the exact solution we can complete the tag CONDITIONS prescribing the parameters necessary (PARAMETERS)and the solver settings (SOLVERINFO):

In the PARAMETERS tag, FinTime is the final physical time of the simulation, TimeStep is the time-step, NumSteps is the number of steps, IO_CheckSteps is the step-interval when a output file is written, IO_InfoSteps is the step-interval when some information about the simulation are printed to the screen, advx and advy are the advection velocities V_x and V_y, respectively and k is the κ parameter. Note that advx, advy and k are used in the boundary and initial conditions tags as well as in the specification of the advection velocities.

In the SOLVERINFO tag, EQTYPE is the type of equation to be solved, Projection is the spatial projection operator to be used (which in this case is specified to be ‘DisContinuous’), AdvectionType is the advection operator to be adopted (where the VALUE ‘WeakDG’ implies the use of a weak Discontinuous Galerkin technique), UpwindType is the numerical flux to be used at the element interfaces when a discontinuous projection is used, TimeIntegrationMethod allows selecting the time-integration scheme. For additional solver-setting options refer to the User-Guide.

Finally, we need to specify the expansion bases we want to use in each of the three composites or sub-domains (COMPOSITE="..") introduced in section 2.1:

In particular, for all the composites, COMPOSITE="C[i]" with i=1,2,3 we select identical basis functions and polynomial order, where NUMMODES is the number of coefficients we want to use for the basis functions (that is commonly equal to P+1 where P is the polynomial order of the basis functions), TYPE allows selecting the basis functions FIELDS is the solution variable of our problem and COMPOSITE are the mesh regions created by Gmsh. For additional details on the EXPANSIONS tag refer to the User-Guide.