Synopsis

11.1 Synopsis

A useful tool implemented in Nektar++ is the incompressible Navier Stokes solver that allows one to solve the governing equation for viscous Newtonians fluids governed by:

+ u ⋅∇u	= -∇p + ν∇²u + f	(11.1a)
∇⋅u	= 0	(11.1b)

where u is the velocity, p is the specific pressure (including density) and ν the kinematic viscosity.

Various approaches to solve and analyse this set of equations are available in Nektar++ as shwon in table 11.1.

Table 11.1: An overview of the solvers available in Nektar++ for the incompressible Navier-Stokes equations.

Solver	Options
Velocity Correction Scheme	Semi-Implicit
"	Semi-Implicit w/ Weak Pressure
"	Implicit
"	Coordinate Transformation
Smoothed Profile Method	-
Linear Stability Analysis	Direct
"	Adjoint
"	Transient Growth
Steady-State solver	Selective Frequency Damping
Direct (Coupled) Solver	Stokes Problem

11.1.1 Velocity Correction Scheme

The first approach uses a splitting/projection method where the velocity system and the pressure are typically decoupled. Splitting schemes are typically favoured for their numerical efficiency since the velocity and pressure are handled independently, requiring the solution of four (in three dimensions) elliptic systems of rank N (opposed to a single system of rank 4N solved in the Stokes problem). However, a drawback of this approach is the splitting scheme error which is introduced when decoupling the pressure and the velocity system, although this can be made consistent with the overall temporal accuracy of the scheme by appropriate discretisation of the pressure boundary conditions.

The scheme discretises the momentum equation Eq. (11.1a) with a backwards approximation of the time derivative to obtain

n+1 n+1 ∂u- ≃ γ0˜u------^u- ∂t Δt

(11.2)

where ⁿ⁺¹ is an intermediate velocity and is the summation of previous solutions.

With the discrete time derivative, we initially have to solve a pressure Poisson equation of the form

∇2pn+1 = ∇ ⋅(-^u- - N *,n+1) Δt

(11.3)

and use consistent Neumann boundary conditions prescribed as

∂p n+1 [∂u n+1 ] --- = - --- + ν(∇ × ∇ × u )*,n+1 + N*,n+1 ⋅n ∂n ∂t

(11.4)

Here, the advection term is denoted as N^*,n+1 = [u ⋅∇u]^⋆,n+1 where the superscript indicates extrapolation from previous solutions.

The second step solves a Helmholtz problem for each new velocity component [uⁿ⁺¹,vⁿ⁺¹,wⁿ⁺¹] which leads us to

(Δ - -γ0-)un+1 = - ( γ0-)^u+ 1∇pn+1. νΔt νΔt ν

(11.5)

This form of the Velocity Correction scheme is generally referred to as Semi-Implicit scheme, because diffusion terms are treated implicit while advection is treated explicit.

The algorithm follows the general structure outlined in figure 11.1.1. Essentially, it solves for the new pressure pⁿ⁺¹ and velocity uⁿ⁺¹ based on initial conditions at tⁿ = nΔt and boundary conditions. The three-step structure begins with evaluating the (explicit) advection terms. Next, a Poisson problem for the new pressure pⁿ⁺¹ is solved. Finally, a Helmholtz problem is solved for each velocity component (uⁿ⁺¹ = [u,v,w]^T in 3D).

Advection N^*,n+1

Poisson ∇²pⁿ⁺¹

3x Helmholtz λuⁿ⁺¹ + ∇²uⁿ⁺¹Time loop n = n + 1

Figure 11.1: The algorithm of the Velocity Correction scheme to compute pressure and velocity at the new time tⁿ = nΔt.

11.1.1.1 Velocity Correction Scheme with a Weak Pressure formulation

One way to improve the Velocity Correction scheme is the weak pressure formulation. This form uses the same algorithm from figure 11.1.1. However, the scheme uses the extrapolated advection term in the pressure forcing instead of the boundary conditions. This changes the pressure Poisson boundary condition from equation Eq. (11.4) to become

n+1 [ n+1 ] ∂p- = - ∂u- + ν(∇ × ∇ × u)*,n+1 ⋅n. ∂n ∂t

(11.6)

Further details for this scheme can be found in the Developer-Guide.

11.1.1.2 Implicit Velocity Correction Scheme

The implicit solver handles the advection terms implicitly. Effectively, it uses the same formulation as the Velocity Correction scheme described above, but brings the advection operator on the left-hand side through a linearisation. The approach is similar to the work of [46, 11].

The new velocity equation with linearised advection term is

( -γ0- 1- ˜ ) n+1 (-γ0-) 1- n+1 Δ - νΔt + νu ⋅∇ u = - νΔt ^u + ν ∇p

(11.7)

The algorithm follows a similar structure to the Semi-Implicit algorithm introduced above in section 11.1.1. The Poisson problem for the new pressure pⁿ⁺¹ is identical to the weak pressure formulation in section 11.1.1.1. The difference here is using an implicit advection operator that relaxes the Courant-Friedrichs-Levy (CFL) limitation for the time step size. This results in an Advection-Diffusion-Reaction (ADR) problem for the new velocity components.

Advection N^*,n+1

Poisson ∇²pⁿ⁺¹

3x ADR
λuⁿ⁺¹+∇²uⁿ⁺¹+⋅∇uⁿ⁺¹Time loop n = n + 1

Figure 11.2: The algorithm of the Implicit Velocity Correction scheme using an ADR solve for the new velocity components uⁿ⁺¹.

The linearisation of the advection operator uses the approximation [u ⋅∇u]ⁿ⁺¹ ≈ [ ⋅∇u]ⁿ⁺¹ where is an approximate advection velocity. The advection velocity is implemented in two forms. The first form is referred to as Extrapolated as it is based on a simple extrapolation of previous velocity solutions [46]. The second form is called Updated and it is based on a pressure-equation residual that uses the updated pressure gradient ∇pⁿ⁺¹ [11]. They are defined respectively as,

`Extrapolated` ⁿ⁺¹	= ∑_qu^n-q,	(11.8)
`Updated` ⁿ⁺¹	= ∑_qu^n-q -.	(11.9)

The scheme defaults to Extrapolated, see the examples in section 11.11 for how to choose Updated instead.

Note that the advection matrix needs to be updated for every time-step, this potentially leads to increased computational cost when compared to the Semi-Implicit scheme. Also, consider that the solver is linearly-implicit instead of fully-implicit. This means that there are no sub iterations for each time step and thus no free parameters (e.g. tolerance) that need to be defined additionally.

11.1.1.3 Coordinate Transformation

For some problems the physical coordinate system is not the most computationally-efficient. In these cases, there is a coordinate transformation option for the Velocity Correction scheme that allows mapping from the physical coordinates to a numerical coordinate system. More details for this method can be found in the Developer Guide as well as examples on how to use it in section 11.11.

11.1.1.4 Substepping/subcycling the Velocity Correction Scheme

It is possible to use different time steps in the velocity correction scheme using a substepping (also known as subcycling) [42] or auxiliary semi-Lagrangian approach [51]. Originally the scheme was proposed by Maday, Patera and Ronquist who referred to as an operator-integration-factor splitting method [29]

Figure 11.3: Schematic representation of the substepping approach. (a) Making an explicit time step the hyperbolic solution, travelling with a speed a, can be understood as being related to the solution at point x_d (the departure point). (b) Making smaller explicit time steps we can evaluate the solution ϕ(x_d) at the departure point and then use this value to make a semi-Lagrangian discretisation of the implicit components usually associated with diffusion.

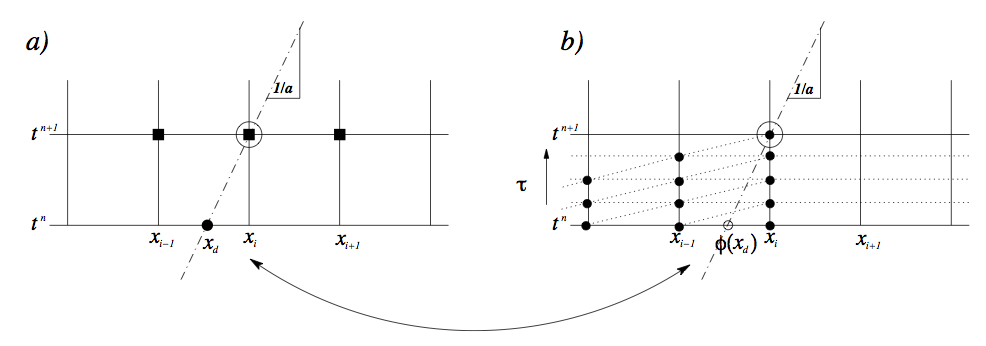
A schematic of the approach can be understood from figure 11.1.1.4 where we observe that smaller time steps can be used for the explicit advection steps whilst a larger overall time step is adopted for the more expensive implicit solve for the diffusion operator. More details of the implementation can be found in [51] and [42]. In the following sections we outline the parameters that can be used to set up this scheme. Since the explicit part is advanced using a DG scheme it is necessary to use a Mixed_CG_Discontinuous expansion with this option.

Note: Some examples of the substepping scheme can be found in the regression tests directory under $NEKHOME/Solver/IncNavierStokesSolver/Tests/ directory: KovaFlow_SubStep_2order.xml, Hex_Kovasnay_SubStep.xml and Tet_Kovasnay_SubStep.xml.

11.1.2 Immersed Boundary Methods: Smoothed Profile Method

The usual way to solve any PDE requires the definition of a well defined domain where the solution is to be determined. Thus, for complex geometries, the meshing process may get cumbersome and, in any case, the solver will have to the meshing process may get cumbersome, and likely struggle to avoid the presence of highly deformed and skewed elements. In addition, when solving cases with moving boundaries, the mesh has to be updated every time step to follow the shape of the boundaries, leading to a very resource and time-consuming simulation that limits the capabilities of the solver.

Immersed Boundary Methods may be very useful in these situations, where the definition of the boundaries requires a very complex mesh to reach convergence. The main idea behind them is the use of a forcing term in the incompressible Navier-Stokes equations in such a way that the mesh does not necessariliy follow the boundaries. The solution in the regions falling outside the boundaries is simply that of the boundaries, forcing the flow to behave as if there were a real object even if the mesh does not represent it. The method presented here is an adaptation of the Smoothed Profile Method [36] extended to a high-order semi-implicit splitting scheme [27, 49]. This method ensures that the no-slip, no-penetration and incompressibility constraints are mathematically enforced. Starting from the incompressible Navier-Stokes equations, the term f_s is added to the right hand side:

∂u-+ u ⋅∇u = - ∇p + ν∇2u + f + f ∂t s

(11.10a)

∇ ⋅u = 0

(11.10b)

The definition of this term depends on the method but, for the Smoothed Profile Method (SPM), it is related to a shape function Φ(x,t) valued 0 in the fluid domain and 1 outside. It is usually defined as:

[ ( ) ] Φ (x,t) = - 1 tanh d(x,t) - 1 , 2 ξ

(11.11)

pict

Figure 11.4: Definition of the shape function Φ close to the boundary of an immersed body.

being ξ a scaling factor [49] and d(x,t) a function representing the distance to the boundary (positive inside the body, negative inside the fluid). If the case to be simulated includes more than one immersed boundaries, the final shape function is calculated by adding the individual ones as long as they do not overlap:

∑ Φ = Φi i

(11.12)

The approach followed during the implementation in Nektar++ is an extension of the Velocity Correction Scheme, using the final velocity obtained with this method as an intermediate velocity to determine the value of the forcing term. The initial equation Eq. (11.10a) is slightly modified and integrated in time by means of a stiffly-stable scheme and, then, split into different smaller parts that are solved separately:

n+1 ∑J -1 n-q J∑-1 γ0u--------q=0-αq-u--- = - βq (u⋅∇u )n-q- ∇(p*+pp )n+1+ ν∇2un+1+f n+1+fsn+1 Δt q=0

(11.13)

∑
˜u-----Jq=-01αq-un--q J∑-1 n- q n+1
Δt = - βq (u⋅∇u ) + f ,
q=0
^u---˜u-= - ∇p *n+1,
Δt
*
γ0u----^u-= ν∇2un+1,
Δt
n+1 *
γ0u------γ0u--= - ∇pn+1 + fn+1
Δt p s

(11.14a)

(11.14b)

(11.14c)

(11.14d)

The new term f_s is defined as follows:

n+1 n+1 * fsn+1 = γ0Φ---(up------u--), Δt

(11.15)

where α_q, β_q and γ₀ are coefficients of the stiffly-stable time integration method and u_p is the velocity of the points that lay outside the boundaries. Thus, the new term is just an acceleration proportional to the difference between the expected and the intermediate velocity, forcing the flow to follow the shapes defined by Φ and u_p.

11.1.3 Linear Stability Analysis

Hydrodynamic stability is an important part of fluid-mechanics that has a relevant role in understanding how an unstable flow can evolve into a turbulent state of motion with chaotic three-dimensional vorticity fields and a broad spectrum of small temporal and spatial scales. The essential problems of hydrodynamic stability were recognised and formulated in 19th century, notably by Helmholtz, Kelvin, Rayleigh and Reynolds.

Conventional linear stability assumes a normal representation of the perturbation fields that can be represented as independent wave packets, meaning that the system is self-adjoint. The main aim of the global stability analysis is to evaluate the amplitude of the eigenmodes as time grows and tends to infinity. However, in most industrial applications, it is also interesting to study the behaviour at intermediate states that might affects significantly the functionality and performance of a device. The study of the transient evolution of the perturbations is seen to be strictly related to the non-normality of the linearised Navier-Stokes equations, therefore the normality assumption of the system is no longer assumed. The eigenmodes of a non-normal system do not evolve independently and their interaction is responsible for a non-negligible transient growth of the energy. Conventional stability analysis generally does not capture this behaviour, therefore other techniques should be used.

A popular approach to study the hydrodynamic stability of flows consists in performing a direct numerical simulation of the linearised Navier-Stokes equations using iterative methods for computing the solution of the associated eigenproblem. However, since linearly stable flows could show a transient increment of energy, it is necessary to extend this analysis considering the combined effect of the direct and adjoint evolution operators. This phenomenon has noteworthy importance in several engineering applications and it is known as transient growth.

In Nektar++ it is then possible to use the following tools to perform stability analysis:

direct stability analysis;
adjoint stability analysis;
transient growth analysis;

11.1.3.1 Direct stability analysis

The equations that describe the evolution of an infinitesimal disturbance in the flow can be derived decomposing the solution into a basic state (U,p) and a perturbed state U + εu′ with ε « 1 that both satisfy the Navier-Stokes equations. Substituting into the Navier-Stokes equations and considering that the quadratic terms u′⋅∇u′ can be neglected, we obtain the linearised Navier-Stokes equations:

∂u ′ ----+ U ⋅∇u ′ + u ′ ⋅∇U = - ∇p + ν∇2u ′ + f ∂t

(11.16a)

∇ ⋅u ′ = 0

(11.16b)

The linearised Navier-Stokes equations are identical in form to the non-linear equation, except for the non-linear advection term. Therefore the numerical techniques used for solving Navier-Stokes equations can still be applied as long as the non-linear term is substituted with the linearised one. It is possible to define the linear operator that evolved the perturbation forward in time:

u′(x,t) = A (U )u ′(x,0)

(11.17)

Let us assume that the base flow U is steady, then the perturbations are autonomous and we can assume that:

′ ′ u (x,t) = q (x) exp(λt) where λ = σ + iω

(11.18)

Then we obtain the associated eigenproblem:

′ ′ A (U )q = λq

(11.19)

The dominant eigenvalue determines the behaviour of the flow. If the real part is positive then there exist exponentially growing solutions. Conversely, if all the eigenvalues have negative real part then the flow is linearly stable. If the real part of the eigenvalue is zero, it is a bifurcation point.

11.1.3.2 Adjoint Stability Analysis

The adjoint of a linear operator is one of the most important concepts in functional analysis and it plays an important role in understanding transition to turbulence. Let us write the linearised Navier-Stokes equation in a compact form:

( | ) ---∂t --(U-⋅∇-)+-(∇U-)⋅+-R1e∇2--|- ∇- Hq = 0 where H = ∇ ⋅ | 0

(11.20)

The adjoint operator H^* is defined as:

* * ⟨Hq, q ⟩ = ⟨q,H q ⟩

(11.21)

Integrating by parts and employing the divergence theorem, it is possible to express the adjoint equations:

∂u* 1 - ----+ (U ⋅∇ )u* + (∇U )T ⋅u * = - ∇p * +-∇2u ∂t Re

(11.22a)

∇ ⋅u * = 0

(11.22b)

The adjoint fields are in fact related to the concept of receptivity. The value of the adjoint velocity at a point in the flow indicates the response that arises from an unsteady momentum source at that point. The adjoint pressure and the adjoint stream function play instead the same role for mass and vorticity sources respectively. Therefore, the adjoint modes can be seen as a powerful tool to understand where to act in order to ease/inhibit the transition.

11.1.3.3 Transient Growth Analysis

Transient growth is a phenomenon that occurs when a flow that is linearly stable, but whose perturbations exhibit a non-negligible transient response due to regions of localised convective instabilities. This situation is common in many engineering applications, for example in open flows where the geometry is complex, producing a steep variation of the base flow. Therefore, the main question to answer is if it exists a bounded solution that exhibit large growth before inevitably decaying. Let us introduce a norm to quantify the size of a perturbation. It is physically meaningful to use the total kinetic energy of a perturbation on the domain Ω. This is convenient because it is directly associated with the standard-L2 inner product:

A (τ )v = σu, ∥u∥ = 1

(11.23)

where σ = ∥u′(τ )∥ . This is no other than the singular value decomposition of A(τ). The phenomenology of the transient growth can be explained considering the non-normality of the linearised Navier-Stokes evolution operator. This can be simply understood using the simple geometric example showed in figure 11.1.3.3. Let us assume a unit-length vector f represented in a non-orthogonal basis .This vector is defined as the difference of the nearly collinear vectors Φ₁ and Φ₂. With the time progression, the component of these two vectors decrease respectively by 20% and 50%. The vector f increases substantially in length before decaying to zero. Thus, the superposition of decaying non-orthogonal eigenmode can produce in short term a growth in the norm of the perturbations.

Figure 11.5: Geometric interpretation of the transient growth. Adapted from Schmid, 2007

11.1.4 Steady-state solver using Selective Frequency Damping

To compute linear stability analysis, the choice of the base flow, around which the system will be linearised, is crucial. If one wants to use the steady-state solution of the Navier-Stokes equations as base flow, a steady-state solver is implemented in Nektar++. The method used is the encapsulated formulation of the Selective Frequency Damping method [21]. Unstable steady base flows can be obtained with this method. The SFD method is based on the filtering and control of unstable temporal frequencies within the flow. The time continuous formulation of the SFD method is

{˙q = N S(q)- χ (q - ¯q), q- ¯q ˙¯q = -Δ-.

(11.24)

where q represents the problem unknown(s), the dot represents the time derivative, NS represents the Navier-Stokes equations, χ ∈ ℝ₊ is the control coefficient, q is a filtered version of q, and Δ ∈ ℝ₊^* is the filter width of a first-order low-pass time filter. The steady-state solution is reached when q = q.

The convergence of the method towards a steady-state solution depends on the choice of the parameters χ and Δ. They have to be carefully chosen: if they are too small, the instabilities within the flow can not be damped; but if they are too large, the method may converge extremely slowly. If the dominant eigenvalue of the flow studied is known (and given as input), the algorithm implemented can automatically select parameters that ensure a fast convergence of the SFD method. Most of the time, the dominant eigenvalue is not know, that is why an adaptive algorithm that adapts χ and Δ all along the solver execution is also implemented.

Note that this method can not be applied for flows with a pure exponential growth of the instabilities (e.g. jet flow within a pipe). In other words, if the frequency of the dominant eigenvalue is zero, then the SFD method is not a suitable tool to obtain a steady-state solution.

11.1.5 Direct solver (coupled approach)

The second approach consists of directly solving the matrix problem arising from the discretization of the Stokes problem. The direct solution of the Stokes system introduces the problem of appropriate spaces for the velocity and the pressure systems to satisfy the inf-sup condition and it requires the solution of the full velocity-pressure system. However, if a discontinuous pressure space is used then all but the constant mode of the pressure system can be decoupled from the velocity. When implementing this approach with a spectral/hp element discretization, the remaining velocity system may then also be statically condensed to decouple the so called interior elemental degrees of freedom, reducing the Stokes problem to a smaller system expressed on the elemental boundaries. The direct solution of the Stokes problem provides a very natural setting for the solution of the pressure system which is not easily dealt with in a splitting scheme. Further, the solution of the full coupled velocity system allows the introduction of a spatially varying viscosity, which arise for non-Newtonian flows, with only minor modifications.

Note: The coupled solver is only supported for two-dimensional or quasi-3D problems, and only using a direct solver (e.g. DirectStaticCond) which prevents its use in parallel.

We consider the weak form of the Stokes problem for the velocity field u = [u,v]^T and the pressure field p:

(∇ ϕ,ν∇u ) - (∇ ⋅ϕ,p) = (ϕ, f)

(11.25a)

(q,∇ ⋅u) = 0

(11.25b)

where the components of A,B and C are ∇ϕ_b,ν∇ub, ∇ϕ_b,ν∇ui and ∇ϕ_i,ν∇ui and the components D_b and D_i are q,∇ub and q,∇ui. The indices b and i refer to the degrees of freedom on the elemental boundary and interior respectively. In constructing the system we have lumped the contributions form each component of the velocity field into matrices A,B and C. However, we note that for a Newtonian fluid the contribution from each field is decoupled. Since the interior degrees of freedom of the velocity field do not overlap, the matrix C is block diagonal and to take advantage of this structure we can statically condense out the C matrix to obtain the system:

⌊ -1 T T - 1 ⌋ ⌊ ⌋ ⌊ -1 ⌋ | A - BC B D b - BC Di 0 | | ub | | fb - BC fi | ⌈ Db - DTi C- 1BT - DTi C -1Di 0 ⌉ ⌈ p ⌉ = ⌈ - DTi C -1fi ⌉ BT Di C ui fi

(11.26)

To extend the above Stokes solver to an unsteady Navier-Stokes solver we first introduce the unsteady term, ∂u∕∂t, into the Stokes problem. This has the principal effect of modifying the weak Laplacian operator ∇ϕ,ν∇u] into a weak Helmholtz operator ∇ϕ,ν∇u) -λ(ϕ,u where λ depends on the time integration scheme. The second modification requires the explicit discretisation of the non-linear terms in a similar manner to the splitting scheme and this term is then introduced as the forcing term f. For more details see [1, 43].

[next] [prev] [prev-tail] [front] [up]