|
Nektar++
|
|
Nektar++
|
Abstraction of a global continuous one-dimensional spectral/hp element expansion which approximates the solution of a set of partial differential equations. More...
#include <ContField1D.h>
Public Member Functions | |
| ContField1D () | |
| Default constructor. | |
| ContField1D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph1D, const std::string &variable) | |
| Set up global continuous field based on an input mesh and boundary conditions. | |
| ContField1D (const ContField1D &In) | |
| Copy constructor. | |
| ContField1D (const LibUtilities::SessionReaderSharedPtr &pSession, const ExpList1D &In) | |
| Copy constructor. | |
| virtual | ~ContField1D () |
| Destructor. | |
| void | FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
Perform global forward transformation of a function 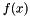 ,. ,. | |
| void | BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| This function performs the backward transformation of the spectral/hp element expansion. | |
| void | MultiplyByInvMassMatrix (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| const Array< OneD, const MultiRegions::ExpListSharedPtr > & | GetBndCondExpansions () |
| Return the boundary conditions expansion. | |
| const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > & | GetBndConditions () |
| void | GlobalToLocal (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
Scatters from the global coefficients  to the local coefficients to the local coefficients  . . | |
| void | LocalToGlobal () |
Gathers the global coefficients  from the local coefficients from the local coefficients  . . | |
| void | Assemble () |
Assembles the global coefficients  from the local coefficients from the local coefficients  . . | |
| void | Assemble (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
Assembles the global coefficients  from the local coefficients from the local coefficients  . . | |
| const AssemblyMapCGSharedPtr & | GetLocalToGlobalMap () const |
| Returns the map from local to global level. | |
| void | IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
Calculates the inner product of a function 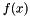 with respect to all global expansion modes with respect to all global expansion modes 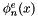 . . | |
| void | GeneralMatrixOp (const GlobalMatrixKey &gkey, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| Calculates the result of the multiplication of a global matrix of type specified by mkey with a vector given by inarray. | |
 Public Member Functions inherited from Nektar::MultiRegions::DisContField1D Public Member Functions inherited from Nektar::MultiRegions::DisContField1D | |
| DisContField1D () | |
| Default constructor. | |
| DisContField1D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph1D, const std::string &variable, const bool SetUpJustDG=true) | |
| Constructs a 1D discontinuous field based on a mesh and boundary conditions. | |
| DisContField1D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph1D, const SpatialDomains::CompositeMap &domain, const SpatialDomains::BoundaryConditions &Allbcs, const std::string &variable, bool SetToOneSpaceDimensions=false) | |
| Constructor for a DisContField1D from a List of subdomains New Constructor for arterial network. | |
| DisContField1D (const DisContField1D &In) | |
| Constructs a 1D discontinuous field based on an existing field. | |
| DisContField1D (const ExpList1D &In) | |
| Constructs a 1D discontinuous field based on an existing field. (needed in order to use ContField( const ExpList1D &In) constructor. | |
| virtual | ~DisContField1D () |
| Destructor. | |
| GlobalLinSysSharedPtr | GetGlobalBndLinSys (const GlobalLinSysKey &mkey) |
| For a given key, returns the associated global linear system. | |
| vector< bool > & | GetNegatedFluxNormal (void) |
 Public Member Functions inherited from Nektar::MultiRegions::ExpList1D Public Member Functions inherited from Nektar::MultiRegions::ExpList1D | |
| ExpList1D () | |
| The default constructor. | |
| ExpList1D (const ExpList1D &In, const bool DeclareCoeffPhysArrays=true) | |
| The copy constructor. | |
| ExpList1D (const LibUtilities::SessionReaderSharedPtr &pSession, const LibUtilities::BasisKey &Ba, const SpatialDomains::MeshGraphSharedPtr &graph1D) | |
| Construct an ExpList1D from a given graph. | |
| ExpList1D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph1D, const bool DeclareCoeffPhysArrays=true) | |
| This constructor sets up a list of local expansions based on an input graph1D. | |
| ExpList1D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph1D, const SpatialDomains::CompositeMap &domain, const bool DeclareCoeffPhysArrays=true, const std::string var="DefaultVar", bool SetToOneSpaceDimension=false) | |
| This constructor sets up a list of local expansions based on an input compositeMap. | |
| ExpList1D (const SpatialDomains::CompositeMap &domain, const SpatialDomains::MeshGraphSharedPtr &graph2D, const bool DeclareCoeffPhysArrays=true, const std::string variable="DefaultVar") | |
| Specialised constructor for Neumann boundary conditions in DisContField2D and ContField2D. | |
| ExpList1D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::CompositeMap &domain, const SpatialDomains::MeshGraphSharedPtr &graph1D, int i, const bool DeclareCoeffPhysArrays=true) | |
| ExpList1D (const LibUtilities::SessionReaderSharedPtr &pSession, const Array< OneD, const ExpListSharedPtr > &bndConstraint, const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > &bndCond, const LocalRegions::ExpansionVector &locexp, const SpatialDomains::MeshGraphSharedPtr &graph2D, const PeriodicMap &periodicEdges, const bool DeclareCoeffPhysArrays=true, const std::string variable="DefaultVar") | |
| Specialised constructor for trace expansions. | |
| virtual | ~ExpList1D () |
| Destructor. | |
| void | PostProcess (LibUtilities::KernelSharedPtr kernel, Array< OneD, NekDouble > &inarray, Array< OneD, NekDouble > &outarray, NekDouble h, int elmId=0) |
| Performs the post-processing on a specified element. | |
| void | PeriodicEval (Array< OneD, NekDouble > &inarray1, Array< OneD, NekDouble > &inarray2, NekDouble h, int nmodes, Array< OneD, NekDouble > &outarray) |
| Evaluates the global spectral/hp expansion at some arbitray set of points. | |
| void | ParNormalSign (Array< OneD, NekDouble > &normsign) |
| Set up the normals on each expansion. | |
 Public Member Functions inherited from Nektar::MultiRegions::ExpList Public Member Functions inherited from Nektar::MultiRegions::ExpList | |
| ExpList () | |
| The default constructor. | |
| ExpList (const LibUtilities::SessionReaderSharedPtr &pSession) | |
| The default constructor. | |
| ExpList (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &pGraph) | |
| The default constructor. | |
| ExpList (const ExpList &in, const bool DeclareCoeffPhysArrays=true) | |
| The copy constructor. | |
| virtual | ~ExpList () |
| The default destructor. | |
| int | GetNcoeffs (void) const |
Returns the total number of local degrees of freedom 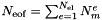 . . | |
| int | GetNcoeffs (const int eid) const |
| Returns the total number of local degrees of freedom for element eid. | |
| ExpansionType | GetExpType (void) |
| Returns the type of the expansion. | |
| void | SetExpType (ExpansionType Type) |
| Returns the type of the expansion. | |
| int | EvalBasisNumModesMax (void) const |
| Evaulates the maximum number of modes in the elemental basis order over all elements. | |
| const Array< OneD, int > | EvalBasisNumModesMaxPerExp (void) const |
| Returns the vector of the number of modes in the elemental basis order over all elements. | |
| int | GetTotPoints (void) const |
Returns the total number of quadrature points m_npoints 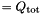 . . | |
| int | GetTotPoints (const int eid) const |
Returns the total number of quadrature points for eid's element 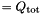 . . | |
| int | GetNpoints (void) const |
Returns the total number of quadrature points m_npoints 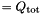 . . | |
| int | Get1DScaledTotPoints (const NekDouble scale) const |
| Returns the total number of qudature points scaled by the factor scale on each 1D direction. | |
| void | SetWaveSpace (const bool wavespace) |
| Sets the wave space to the one of the possible configuration true or false. | |
| void | SetModifiedBasis (const bool modbasis) |
| Set Modified Basis for the stability analysis. | |
| void | SetPhys (int i, NekDouble val) |
| Set the i th value of m_phys to value val. | |
| bool | GetWaveSpace (void) const |
| This function returns the third direction expansion condition, which can be in wave space (coefficient) or not It is stored in the variable m_WaveSpace. | |
| void | SetPhys (const Array< OneD, const NekDouble > &inarray) |
| Fills the array m_phys. | |
| void | SetPhysArray (Array< OneD, NekDouble > &inarray) |
| Sets the array m_phys. | |
| void | SetPhysState (const bool physState) |
This function manually sets whether the array of physical values 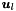 (implemented as m_phys) is filled or not. (implemented as m_phys) is filled or not. | |
| bool | GetPhysState (void) const |
This function indicates whether the array of physical values 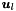 (implemented as m_phys) is filled or not. (implemented as m_phys) is filled or not. | |
| NekDouble | PhysIntegral (void) |
This function integrates a function  over the domain consisting of all the elements of the expansion. over the domain consisting of all the elements of the expansion. | |
| NekDouble | PhysIntegral (const Array< OneD, const NekDouble > &inarray) |
This function integrates a function  over the domain consisting of all the elements of the expansion. over the domain consisting of all the elements of the expansion. | |
| void | IProductWRTBase_IterPerExp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
This function calculates the inner product of a function  with respect to all {local} expansion modes with respect to all {local} expansion modes 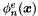 . . | |
| void | IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
This function calculates the inner product of a function  with respect to the derivative (in direction. with respect to the derivative (in direction. | |
| void | FwdTrans_IterPerExp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
This function elementally evaluates the forward transformation of a function 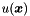 onto the global spectral/hp expansion. onto the global spectral/hp expansion. | |
| void | MultiplyByElmtInvMass (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function elementally mulplies the coefficient space of Sin my the elemental inverse of the mass matrix. | |
| void | SmoothField (Array< OneD, NekDouble > &field) |
| Smooth a field across elements. | |
| void | HelmSolve (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const FlagList &flags, const StdRegions::ConstFactorMap &factors, const StdRegions::VarCoeffMap &varcoeff=StdRegions::NullVarCoeffMap, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solve helmholtz problem. | |
| void | LinearAdvectionDiffusionReactionSolve (const Array< OneD, Array< OneD, NekDouble > > &velocity, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const NekDouble lambda, CoeffState coeffstate=eLocal, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solve Advection Diffusion Reaction. | |
| void | LinearAdvectionReactionSolve (const Array< OneD, Array< OneD, NekDouble > > &velocity, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const NekDouble lambda, CoeffState coeffstate=eLocal, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solve Advection Diffusion Reaction. | |
| void | FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| void | BwdTrans_IterPerExp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function elementally evaluates the backward transformation of the global spectral/hp element expansion. | |
| void | GetCoords (Array< OneD, NekDouble > &coord_0, Array< OneD, NekDouble > &coord_1=NullNekDouble1DArray, Array< OneD, NekDouble > &coord_2=NullNekDouble1DArray) |
This function calculates the coordinates of all the elemental quadrature points 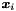 . . | |
| void | HomogeneousFwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal, bool Shuff=true, bool UnShuff=true) |
| void | HomogeneousBwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal, bool Shuff=true, bool UnShuff=true) |
| void | DealiasedProd (const Array< OneD, NekDouble > &inarray1, const Array< OneD, NekDouble > &inarray2, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| void | GetBCValues (Array< OneD, NekDouble > &BndVals, const Array< OneD, NekDouble > &TotField, int BndID) |
| void | NormVectorIProductWRTBase (Array< OneD, const NekDouble > &V1, Array< OneD, const NekDouble > &V2, Array< OneD, NekDouble > &outarray, int BndID) |
| void | ApplyGeomInfo () |
| Apply geometry information to each expansion. | |
| void | WriteTecplotHeader (std::ofstream &outfile, std::string var="") |
| void | WriteTecplotZone (std::ofstream &outfile, int expansion=-1) |
| void | WriteTecplotField (std::ofstream &outfile, int expansion=-1) |
| void | WriteTecplotConnectivity (std::ofstream &outfile, int expansion=-1) |
| void | WriteVtkHeader (std::ofstream &outfile) |
| void | WriteVtkFooter (std::ofstream &outfile) |
| void | WriteVtkPieceHeader (std::ofstream &outfile, int expansion) |
| void | WriteVtkPieceFooter (std::ofstream &outfile, int expansion) |
| void | WriteVtkPieceData (std::ofstream &outfile, int expansion, std::string var="v") |
| int | GetCoordim (int eid) |
| This function returns the dimension of the coordinates of the element eid. | |
| void | SetCoeff (int i, NekDouble val) |
| Set the i th coefficiient in m_coeffs to value val. | |
| void | SetCoeffs (int i, NekDouble val) |
| Set the i th coefficiient in m_coeffs to value val. | |
| void | SetCoeffsArray (Array< OneD, NekDouble > &inarray) |
| Set the m_coeffs array to inarray. | |
| const Array< OneD, const NekDouble > & | GetCoeffs () const |
This function returns (a reference to) the array  (implemented as m_coeffs) containing all local expansion coefficients. (implemented as m_coeffs) containing all local expansion coefficients. | |
| void | ImposeDirichletConditions (Array< OneD, NekDouble > &outarray) |
| Impose Dirichlet Boundary Conditions onto Array. | |
| void | FillBndCondFromField (void) |
| Fill Bnd Condition expansion from the values stored in expansion. | |
| void | GlobalToLocal (void) |
| Put the coefficients into local ordering and place in m_coeffs. | |
| NekDouble | GetCoeff (int i) |
| Get the i th value (coefficient) of m_coeffs. | |
| NekDouble | GetCoeffs (int i) |
| Get the i th value (coefficient) of m_coeffs. | |
| const Array< OneD, const NekDouble > & | GetPhys () const |
This function returns (a reference to) the array 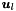 (implemented as m_phys) containing the function (implemented as m_phys) containing the function 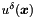 evaluated at the quadrature points. evaluated at the quadrature points. | |
| NekDouble | Linf (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &soln=NullNekDouble1DArray) |
This function calculates the 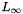 error of the global spectral/hp element approximation. error of the global spectral/hp element approximation. | |
| NekDouble | L2 (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &soln=NullNekDouble1DArray) |
This function calculates the 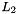 error with respect to soln of the global spectral/hp element approximation. error with respect to soln of the global spectral/hp element approximation. | |
| NekDouble | H1 (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &soln=NullNekDouble1DArray) |
Calculates the 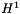 error of the global spectral/hp element approximation. error of the global spectral/hp element approximation. | |
| NekDouble | Integral (const Array< OneD, const NekDouble > &inarray) |
| Array< OneD, const NekDouble > | HomogeneousEnergy (void) |
| This function calculates the energy associated with each one of the modesof a 3D homogeneous nD expansion. | |
| void | SetHomo1DSpecVanVisc (Array< OneD, NekDouble > visc) |
| This function sets the Spectral Vanishing Viscosity in homogeneous1D expansion. | |
| Array< OneD, const unsigned int > | GetZIDs (void) |
| This function returns a vector containing the wave numbers in z-direction associated with the 3D homogenous expansion. Required if a parellelisation is applied in the Fourier direction. | |
| LibUtilities::TranspositionSharedPtr | GetTransposition (void) |
| This function returns the transposition class associaed with the homogeneous expansion. | |
| NekDouble | GetHomoLen (void) |
| This function returns the Width of homogeneous direction associaed with the homogeneous expansion. | |
| Array< OneD, const unsigned int > | GetYIDs (void) |
| This function returns a vector containing the wave numbers in y-direction associated with the 3D homogenous expansion. Required if a parellelisation is applied in the Fourier direction. | |
| void | PhysInterp1DScaled (const NekDouble scale, const Array< OneD, NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function interpolates the physical space points in inarray to outarray using the same points defined in the expansion but where the number of points are rescaled by 1DScale. | |
| void | PhysGalerkinProjection1DScaled (const NekDouble scale, const Array< OneD, NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function Galerkin projects the physical space points in inarray to outarray where inarray is assumed to be defined in the expansion but where the number of points are rescaled by 1DScale. | |
| int | GetExpSize (void) |
| This function returns the number of elements in the expansion. | |
| int | GetNumElmts (void) |
| This function returns the number of elements in the expansion which may be different for a homogeoenous extended expansionp. | |
| const boost::shared_ptr < LocalRegions::ExpansionVector > | GetExp () const |
| This function returns the vector of elements in the expansion. | |
| LocalRegions::ExpansionSharedPtr & | GetExp (int n) const |
This function returns (a shared pointer to) the local elemental expansion of the 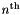 element. element. | |
| LocalRegions::ExpansionSharedPtr & | GetExp (const Array< OneD, const NekDouble > &gloCoord) |
| This function returns (a shared pointer to) the local elemental expansion containing the arbitrary point given by gloCoord. | |
| int | GetExpIndex (const Array< OneD, const NekDouble > &gloCoord, NekDouble tol=0.0, bool returnNearestElmt=false) |
| int | GetExpIndex (const Array< OneD, const NekDouble > &gloCoords, Array< OneD, NekDouble > &locCoords, NekDouble tol=0.0, bool returnNearestElmt=false) |
| int | GetCoeff_Offset (int n) const |
| Get the start offset position for a global list of m_coeffs correspoinding to element n. | |
| int | GetPhys_Offset (int n) const |
| Get the start offset position for a global list of m_phys correspoinding to element n. | |
| int | GetOffset_Elmt_Id (int n) const |
| Get the element id associated with the n th consecutive block of data in m_phys and m_coeffs. | |
| Array< OneD, NekDouble > & | UpdateCoeffs () |
This function returns (a reference to) the array  (implemented as m_coeffs) containing all local expansion coefficients. (implemented as m_coeffs) containing all local expansion coefficients. | |
| Array< OneD, NekDouble > & | UpdatePhys () |
This function returns (a reference to) the array 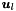 (implemented as m_phys) containing the function (implemented as m_phys) containing the function 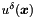 evaluated at the quadrature points. evaluated at the quadrature points. | |
| void | PhysDeriv (Direction edir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d) |
| void | PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray) |
This function discretely evaluates the derivative of a function  on the domain consisting of all elements of the expansion. on the domain consisting of all elements of the expansion. | |
| void | PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d) |
| boost::shared_ptr< ExpList > & | UpdateBndCondExpansion (int i) |
| void | Upwind (const Array< OneD, const Array< OneD, NekDouble > > &Vec, const Array< OneD, const NekDouble > &Fwd, const Array< OneD, const NekDouble > &Bwd, Array< OneD, NekDouble > &Upwind) |
| void | Upwind (const Array< OneD, const NekDouble > &Vn, const Array< OneD, const NekDouble > &Fwd, const Array< OneD, const NekDouble > &Bwd, Array< OneD, NekDouble > &Upwind) |
| boost::shared_ptr< ExpList > & | GetTrace () |
| boost::shared_ptr < AssemblyMapDG > & | GetTraceMap (void) |
| const Array< OneD, const int > & | GetTraceBndMap (void) |
| void | GetNormals (Array< OneD, Array< OneD, NekDouble > > &normals) |
| void | AddTraceIntegral (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray) |
| void | AddTraceIntegral (const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray) |
| void | AddFwdBwdTraceIntegral (const Array< OneD, const NekDouble > &Fwd, const Array< OneD, const NekDouble > &Bwd, Array< OneD, NekDouble > &outarray) |
| void | GetFwdBwdTracePhys (Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| void | GetFwdBwdTracePhys (const Array< OneD, const NekDouble > &field, Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| void | ExtractTracePhys (Array< OneD, NekDouble > &outarray) |
| void | ExtractTracePhys (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| Array< OneD, SpatialDomains::BoundaryConditionShPtr > & | UpdateBndConditions () |
| void | EvaluateBoundaryConditions (const NekDouble time=0.0, const std::string varName="", const NekDouble=NekConstants::kNekUnsetDouble, const NekDouble=NekConstants::kNekUnsetDouble) |
| void | GeneralMatrixOp_IterPerExp (const GlobalMatrixKey &gkey, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| void | SetUpPhysNormals () |
| void | GetBoundaryToElmtMap (Array< OneD, int > &ElmtID, Array< OneD, int > &EdgeID) |
| void | GeneralGetFieldDefinitions (std::vector< LibUtilities::FieldDefinitionsSharedPtr > &fielddef, int NumHomoDir=0, Array< OneD, LibUtilities::BasisSharedPtr > &HomoBasis=LibUtilities::NullBasisSharedPtr1DArray, std::vector< NekDouble > &HomoLen=LibUtilities::NullNekDoubleVector, std::vector< unsigned int > &HomoZIDs=LibUtilities::NullUnsignedIntVector, std::vector< unsigned int > &HomoYIDs=LibUtilities::NullUnsignedIntVector) |
| const NekOptimize::GlobalOptParamSharedPtr & | GetGlobalOptParam (void) |
| map< int, RobinBCInfoSharedPtr > | GetRobinBCInfo () |
| void | GetPeriodicEntities (PeriodicMap &periodicVerts, PeriodicMap &periodicEdges, PeriodicMap &periodicFaces=NullPeriodicMap) |
| std::vector < LibUtilities::FieldDefinitionsSharedPtr > | GetFieldDefinitions () |
| void | GetFieldDefinitions (std::vector< LibUtilities::FieldDefinitionsSharedPtr > &fielddef) |
| void | AppendFieldData (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata) |
| Append the element data listed in elements fielddef->m_ElementIDs onto fielddata. | |
| void | AppendFieldData (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata, Array< OneD, NekDouble > &coeffs) |
| Append the data in coeffs listed in elements fielddef->m_ElementIDs onto fielddata. | |
| void | ExtractElmtDataToCoeffs (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata, std::string &field, Array< OneD, NekDouble > &coeffs) |
| Extract the data in fielddata into the coeffs using the basic ExpList Elemental expansions rather than planes in homogeneous case. | |
| void | ExtractCoeffsToCoeffs (const boost::shared_ptr< ExpList > &fromExpList, const Array< OneD, const NekDouble > &fromCoeffs, Array< OneD, NekDouble > &toCoeffs) |
| Extract the data from fromField using fromExpList the coeffs using the basic ExpList Elemental expansions rather than planes in homogeneous case. | |
| void | ExtractDataToCoeffs (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata, std::string &field, Array< OneD, NekDouble > &coeffs) |
| Extract the data in fielddata into the coeffs. | |
| boost::shared_ptr< ExpList > | GetSharedThisPtr () |
| Returns a shared pointer to the current object. | |
| boost::shared_ptr < LibUtilities::SessionReader > | GetSession () |
| Returns the session object. | |
| boost::shared_ptr < LibUtilities::Comm > | GetComm () |
| Returns the comm object. | |
| SpatialDomains::MeshGraphSharedPtr | GetGraph () |
| LibUtilities::BasisSharedPtr | GetHomogeneousBasis (void) |
| boost::shared_ptr< ExpList > & | GetPlane (int n) |
Protected Attributes | |
| AssemblyMapCGSharedPtr | m_locToGloMap |
| (A shared pointer to) the object which contains all the required information for the transformation from local to global degrees of freedom. | |
| CoeffState | m_coeffState |
| A enum list declaring how to interpret coeffs, i.e. eLocal, eHybrid or eGlobal. | |
| GlobalMatrixMapShPtr | m_globalMat |
| (A shared pointer to) a list which collects all the global matrices being assembled, such that they should be constructed only once. | |
| LibUtilities::NekManager < GlobalLinSysKey, GlobalLinSys > | m_globalLinSysManager |
| A manager which collects all the global linear systems being assembled, such that they should be constructed only once. | |
 Protected Attributes inherited from Nektar::MultiRegions::DisContField1D Protected Attributes inherited from Nektar::MultiRegions::DisContField1D | |
| int | m_numDirBndCondExpansions |
| The number of boundary segments on which Dirichlet boundary conditions are imposed. | |
| Array< OneD, MultiRegions::ExpListSharedPtr > | m_bndCondExpansions |
| Discretised boundary conditions. | |
| Array< OneD, SpatialDomains::BoundaryConditionShPtr > | m_bndConditions |
| An array which contains the information about the boundary condition on the different boundary regions. | |
| GlobalLinSysMapShPtr | m_globalBndMat |
| Global boundary matrix. | |
| ExpListSharedPtr | m_trace |
| Trace space storage for points between elements. | |
| AssemblyMapDGSharedPtr | m_traceMap |
| Local to global DG mapping for trace space. | |
| std::set< int > | m_boundaryVerts |
| A set storing the global IDs of any boundary edges. | |
| PeriodicMap | m_periodicVerts |
| A map which identifies groups of periodic vertices. | |
| vector< int > | m_periodicFwdCopy |
| A vector indicating degress of freedom which need to be copied from forwards to backwards space in case of a periodic boundary condition. | |
| vector< int > | m_periodicBwdCopy |
| vector< bool > | m_leftAdjacentVerts |
Private Member Functions | |
| GlobalLinSysSharedPtr | GetGlobalLinSys (const GlobalLinSysKey &mkey) |
| Returns the linear system specified by mkey. | |
| GlobalLinSysSharedPtr | GenGlobalLinSys (const GlobalLinSysKey &mkey) |
| void | GlobalSolve (const GlobalLinSysKey &key, const Array< OneD, const NekDouble > &rhs, Array< OneD, NekDouble > &inout, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solve the linear system specified by the key key. | |
| virtual void | v_FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| Perform a forward transform. | |
| virtual void | v_MultiplyByInvMassMatrix (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| virtual void | v_ImposeDirichletConditions (Array< OneD, NekDouble > &outarray) |
| Impose the Dirichlet Boundary Conditions on outarray. | |
| virtual void | v_GlobalToLocal (void) |
Scatters from the global coefficients  to the local coefficients to the local coefficients  . . | |
| virtual void | v_LocalToGlobal (void) |
Gathers the global coefficients  from the local coefficients from the local coefficients  . . | |
| virtual void | v_HelmSolve (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const FlagList &flags, const StdRegions::ConstFactorMap &factors, const StdRegions::VarCoeffMap &varcoeff, const Array< OneD, const NekDouble > &dirForcing) |
| virtual const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > & | v_GetBndConditions () |
| virtual void | v_BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| virtual void | v_IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| virtual void | v_GeneralMatrixOp (const GlobalMatrixKey &gkey, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| Calculates the result of the multiplication of a global matrix of type specified by mkey with a vector given by inarray. | |
Additional Inherited Members | |
 Public Attributes inherited from Nektar::MultiRegions::ExpList Public Attributes inherited from Nektar::MultiRegions::ExpList | |
| ExpansionType | m_expType |
 Protected Member Functions inherited from Nektar::MultiRegions::DisContField1D Protected Member Functions inherited from Nektar::MultiRegions::DisContField1D | |
| void | GenerateBoundaryConditionExpansion (const SpatialDomains::MeshGraphSharedPtr &graph1D, const SpatialDomains::BoundaryConditions &bcs, const std::string variable) |
| Discretises the boundary conditions. | |
| void | FindPeriodicVertices (const SpatialDomains::BoundaryConditions &bcs, const std::string variable) |
| Generate a associative map of periodic vertices in a mesh. | |
| virtual ExpListSharedPtr & | v_GetTrace () |
| virtual AssemblyMapDGSharedPtr & | v_GetTraceMap (void) |
| virtual void | v_AddTraceIntegral (const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray) |
| virtual void | v_GetFwdBwdTracePhys (Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| virtual void | v_GetFwdBwdTracePhys (const Array< OneD, const NekDouble > &field, Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| This method extracts the "forward" and "backward" trace data from the array field and puts the data into output vectors Fwd and Bwd. | |
| virtual void | v_ExtractTracePhys (Array< OneD, NekDouble > &outarray) |
| virtual void | v_ExtractTracePhys (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This method extracts the trace (verts in 1D) from the field inarray and puts the values in outarray. | |
| void | SetBoundaryConditionExpansion (const SpatialDomains::MeshGraphSharedPtr &graph1D, const SpatialDomains::BoundaryConditions &bcs, const std::string variable, Array< OneD, MultiRegions::ExpListSharedPtr > &bndCondExpansions, Array< OneD, SpatialDomains::BoundaryConditionShPtr > &bndConditions) |
| Populates the list of boundary condition expansions. | |
| void | SetMultiDomainBoundaryConditionExpansion (const SpatialDomains::MeshGraphSharedPtr &graph1D, const SpatialDomains::BoundaryConditions &bcs, const std::string variable, Array< OneD, MultiRegions::ExpListSharedPtr > &bndCondExpansions, Array< OneD, SpatialDomains::BoundaryConditionShPtr > &bndConditions, int subdomain) |
| Populates the list of boundary condition expansions in multidomain case. | |
| void | GenerateFieldBnd1D (SpatialDomains::BoundaryConditions &bcs, const std::string variable) |
| virtual map< int, RobinBCInfoSharedPtr > | v_GetRobinBCInfo () |
| virtual const Array< OneD, const MultiRegions::ExpListSharedPtr > & | v_GetBndCondExpansions () |
| virtual const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > & | v_GetBndConditions () |
| virtual MultiRegions::ExpListSharedPtr & | v_UpdateBndCondExpansion (int i) |
| virtual Array< OneD, SpatialDomains::BoundaryConditionShPtr > & | v_UpdateBndConditions () |
| virtual void | v_GetBoundaryToElmtMap (Array< OneD, int > &ElmtID, Array< OneD, int > &VertID) |
| virtual void | v_EvaluateBoundaryConditions (const NekDouble time=0.0, const std::string varName="", const NekDouble x2_in=NekConstants::kNekUnsetDouble, const NekDouble x3_in=NekConstants::kNekUnsetDouble) |
| Evaluate all boundary conditions at a given time.. | |
| virtual void | v_HelmSolve (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const FlagList &flags, const StdRegions::ConstFactorMap &factors, const StdRegions::VarCoeffMap &varcoeff, const Array< OneD, const NekDouble > &dirForcing) |
| Solve the Helmholtz equation. | |
 Static Protected Member Functions inherited from Nektar::MultiRegions::ExpList Static Protected Member Functions inherited from Nektar::MultiRegions::ExpList | |
| static SpatialDomains::BoundaryConditionShPtr | GetBoundaryCondition (const SpatialDomains::BoundaryConditionCollection &collection, unsigned int index, const std::string &variable) |
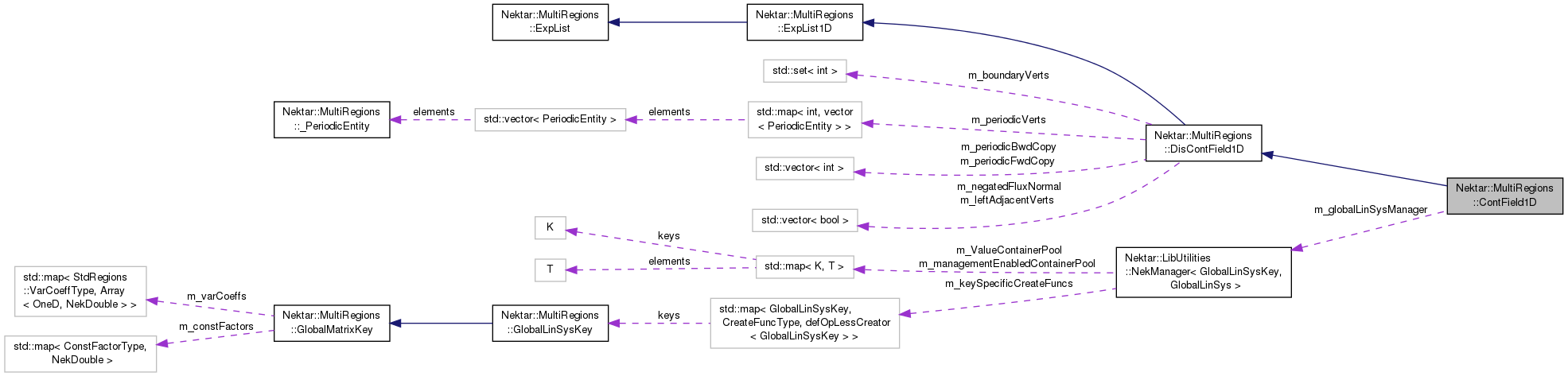
Abstraction of a global continuous one-dimensional spectral/hp element expansion which approximates the solution of a set of partial differential equations.
As opposed to the class #ContExpList1D, the class ContField1D is able to incorporate the boundary conditions imposed to the problem to be solved. Therefore, the class is equipped with three additional data members:
The first data structure, m_bndCondExpansions, contains the point Expansion on the boundary, #m_bndTypes stores information about the type of boundary condition on the different parts of the boundary while #m_bndCondEquations holds the equation of the imposed boundary conditions.
Furthermore, in case of Dirichlet boundary conditions, this class is capable of lifting a known solution satisfying these boundary conditions. If we denote the unknown solution by 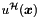 and the known Dirichlet boundary conditions by
and the known Dirichlet boundary conditions by 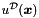 , the expansion then can be decomposed as
, the expansion then can be decomposed as
![\[ u^{\delta}(\boldsymbol{x}_i)=u^{\mathcal{D}}(\boldsymbol{x}_i)+ u^{\mathcal{H}}(\boldsymbol{x}_i)=\sum_{n=0}^{N^{\mathcal{D}}-1} \hat{u}_n^{\mathcal{D}}\Phi_n(\boldsymbol{x}_i)+ \sum_{n={N^{\mathcal{D}}}}^{N_{\mathrm{dof}} -1}\hat{u}_n^{\mathcal{H}} \Phi_n(\boldsymbol{x}_i).\]](form_252.png)
This lifting is accomplished by ordering the known global degrees of freedom, prescribed by the Dirichlet boundary conditions, first in the global array 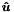 , that is,
, that is,
![\[\boldsymbol{\hat{u}}=\left[ \begin{array}{c} \boldsymbol{\hat{u}}^{\mathcal{D}}\\ \boldsymbol{\hat{u}}^{\mathcal{H}} \end{array} \right].\]](form_254.png)
Such kind of expansions are also referred to as continuoous fields. This class should be used when solving 2D problems using a standard Galerkin approach.
Definition at line 56 of file ContField1D.h.
| Nektar::MultiRegions::ContField1D::ContField1D | ( | ) |
Default constructor.
Constructs an empty 1D continuous field.
Definition at line 86 of file ContField1D.cpp.
| Nektar::MultiRegions::ContField1D::ContField1D | ( | const LibUtilities::SessionReaderSharedPtr & | pSession, |
| const SpatialDomains::MeshGraphSharedPtr & | graph1D, | ||
| const std::string & | variable | ||
| ) |
Set up global continuous field based on an input mesh and boundary conditions.
Given a mesh graph1D, containing information about the domain and the spectral/hp element expansion, this constructor fills the list of local expansions m_exp with the proper expansions, calculates the total number of quadrature points 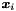 and local expansion coefficients
and local expansion coefficients 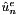 and allocates memory for the arrays m_coeffs and m_phys. Furthermore, it constructs the mapping array (contained in m_locToGloMap) for the transformation between local elemental level and global level, it calculates the total number global expansion coefficients
and allocates memory for the arrays m_coeffs and m_phys. Furthermore, it constructs the mapping array (contained in m_locToGloMap) for the transformation between local elemental level and global level, it calculates the total number global expansion coefficients 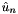 . The constructor also discretises the boundary conditions, specified by the argument bcs, by expressing them in terms of the coefficient of the expansion on the boundary.
. The constructor also discretises the boundary conditions, specified by the argument bcs, by expressing them in terms of the coefficient of the expansion on the boundary.
| graph1D | A 1D mesh, containing information about the domain and the spectral/hp element expansion. |
| bcs | The boundary conditions. |
| variable | An optional parameter to indicate for which variable the field should be constructed. |
Definition at line 117 of file ContField1D.cpp.
References Nektar::MultiRegions::DisContField1D::m_bndCondExpansions, Nektar::MultiRegions::DisContField1D::m_bndConditions, m_locToGloMap, Nektar::MultiRegions::ExpList::m_ncoeffs, Nektar::MultiRegions::DisContField1D::m_periodicVerts, and Nektar::MultiRegions::ExpList::m_session.
| Nektar::MultiRegions::ContField1D::ContField1D | ( | const ContField1D & | In | ) |
Copy constructor.
Constructs a 1D continuous field as a copy of an existing field including all boundary conditions.
| In | Existing continuous field to duplicate. |
Definition at line 142 of file ContField1D.cpp.
| Nektar::MultiRegions::ContField1D::ContField1D | ( | const LibUtilities::SessionReaderSharedPtr & | pSession, |
| const ExpList1D & | In | ||
| ) |
Copy constructor.
Constructs a 1D continuous field as a copy of an existing explist 1D field and adding all the boundary conditions.
| In | Existing explist1D field . |
Definition at line 156 of file ContField1D.cpp.
References m_locToGloMap, and Nektar::MultiRegions::ExpList::m_ncoeffs.
|
virtual |
|
inline |
Assembles the global coefficients  from the local coefficients
from the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}_g[\mbox{map}[e][i]] = \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]+\mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}^{e}[i]$\\ \> \> continue\\ \> continue \end{tabbing}](form_291.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation 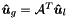 , where
, where 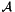 is the
is the 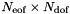 permutation matrix.
permutation matrix.
Definition at line 307 of file ContField1D.h.
References Nektar::MultiRegions::ExpList::m_coeffs, and m_locToGloMap.
Referenced by IProductWRTBase(), MultiplyByInvMassMatrix(), and v_GeneralMatrixOp().
|
inline |
Assembles the global coefficients  from the local coefficients
from the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}_g[\mbox{map}[e][i]] = \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]+\mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}^{e}[i]$\\ \> \> continue\\ \> continue \end{tabbing}](form_291.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation 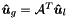 , where
, where 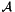 is the
is the 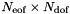 permutation matrix.
permutation matrix.
| inarray | An array of size 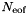 containing the local degrees of freedom containing the local degrees of freedom 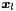 . . |
| outarray | The resulting global degrees of freedom 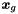 will be stored in this array of size will be stored in this array of size 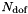 . . |
Definition at line 339 of file ContField1D.h.
References m_locToGloMap.
| void Nektar::MultiRegions::ContField1D::BwdTrans | ( | const Array< OneD, const NekDouble > & | inarray, |
| Array< OneD, NekDouble > & | outarray, | ||
| CoeffState | coeffstate = eLocal |
||
| ) |
This function performs the backward transformation of the spectral/hp element expansion.
Given the coefficients of an expansion, this function evaluates the spectral/hp expansion 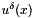 at the quadrature points
at the quadrature points 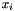 . This operation is evaluated locally by the function ExpList::BwdTrans.
. This operation is evaluated locally by the function ExpList::BwdTrans.
The coefficients of the expansion should be contained in the variable m_coeffs of the ExpList object In. The resulting physical values at the quadrature points 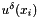 are stored in the array m_phys.
are stored in the array m_phys.
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 227 of file ContField1D.cpp.
References Nektar::MultiRegions::ExpList::BwdTrans_IterPerExp(), Nektar::MultiRegions::eLocal, and Nektar::MultiRegions::ExpList::GlobalToLocal().
Referenced by v_BwdTrans().
| void Nektar::MultiRegions::ContField1D::FwdTrans | ( | const Array< OneD, const NekDouble > & | inarray, |
| Array< OneD, NekDouble > & | outarray, | ||
| CoeffState | coeffstate = eLocal |
||
| ) |
Perform global forward transformation of a function 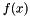 ,.
,.
Given a function 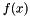 defined at the quadrature points, this function determines the unknown global coefficients
defined at the quadrature points, this function determines the unknown global coefficients 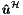 employing a discrete Galerkin projection from physical space to coefficient space. The operation is evaluated by the function GlobalSolve using the global mass matrix.
employing a discrete Galerkin projection from physical space to coefficient space. The operation is evaluated by the function GlobalSolve using the global mass matrix.
The values of the function 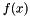 evaluated at the quadrature points
evaluated at the quadrature points 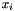 should be contained in the variable m_phys of the ExpList object Sin. The resulting global coefficients
should be contained in the variable m_phys of the ExpList object Sin. The resulting global coefficients 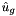 are stored in the array m_coeffs.
are stored in the array m_coeffs.
| inarray | Discrete 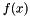 . . |
| outarray | Storage for result. |
| coeffstate |
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 193 of file ContField1D.cpp.
References Nektar::MultiRegions::eGlobal, Nektar::MultiRegions::eLocal, Nektar::StdRegions::eMass, GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), IProductWRTBase(), m_locToGloMap, and Nektar::MultiRegions::ExpList::m_ncoeffs.
Referenced by v_FwdTrans().
| void Nektar::MultiRegions::ContField1D::GeneralMatrixOp | ( | const GlobalMatrixKey & | gkey, |
| const Array< OneD, const NekDouble > & | inarray, | ||
| Array< OneD, NekDouble > & | outarray, | ||
| CoeffState | coeffstate = eLocal |
||
| ) |
Calculates the result of the multiplication of a global matrix of type specified by mkey with a vector given by inarray.
Reimplemented from Nektar::MultiRegions::ExpList.
|
private |
Definition at line 379 of file ContField1D.cpp.
References ASSERTL1, Nektar::MultiRegions::GlobalMatrixKey::LocToGloMapIsDefined(), and m_locToGloMap.
|
inline |
Return the boundary conditions expansion.
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 240 of file ContField1D.h.
References Nektar::MultiRegions::DisContField1D::m_bndCondExpansions.
|
inline |
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 246 of file ContField1D.h.
References Nektar::MultiRegions::DisContField1D::m_bndConditions.
Referenced by v_GetBndConditions().
|
private |
Returns the linear system specified by mkey.
The function searches the map #m_globalLinSys to see if the global matrix has been created before. If not, it calls the function #GenglobalLinSys to generate the requested global system.
| mkey | Key specifying the linear system. |
Definition at line 373 of file ContField1D.cpp.
References m_globalLinSysManager.
Referenced by GlobalSolve().
|
inline |
Returns the map from local to global level.
Definition at line 347 of file ContField1D.h.
References m_locToGloMap.
|
private |
Solve the linear system specified by the key key.
Given a linear system specified by the key key,
![\[\boldsymbol{M}\boldsymbol{\hat{u}}_g=\boldsymbol{\hat{f}},\]](form_265.png)
this function solves this linear system taking into account the boundary conditions specified in the data member m_bndCondExpansions. Therefore, it adds an array 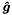 which represents the non-zero surface integral resulting from the weak boundary conditions (e.g. Neumann boundary conditions) to the right hand side, that is,
which represents the non-zero surface integral resulting from the weak boundary conditions (e.g. Neumann boundary conditions) to the right hand side, that is,
![\[\boldsymbol{M}\boldsymbol{\hat{u}}_g=\boldsymbol{\hat{f}}+ \boldsymbol{\hat{g}}.\]](form_267.png)
Furthermore, it lifts the known degrees of freedom which are prescribed by the Dirichlet boundary conditions. As these known coefficients 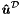 are numbered first in the global coefficient array
are numbered first in the global coefficient array  , the linear system can be decomposed as,
, the linear system can be decomposed as,
![\[\left[\begin{array}{cc} \boldsymbol{M}^{\mathcal{DD}}&\boldsymbol{M}^{\mathcal{DH}}\\ \boldsymbol{M}^{\mathcal{HD}}&\boldsymbol{M}^{\mathcal{HH}} \end{array}\right] \left[\begin{array}{c} \boldsymbol{\hat{u}}^{\mathcal{D}}\\ \boldsymbol{\hat{u}}^{\mathcal{H}} \end{array}\right]= \left[\begin{array}{c} \boldsymbol{\hat{f}}^{\mathcal{D}}\\ \boldsymbol{\hat{f}}^{\mathcal{H}} \end{array}\right]+ \left[\begin{array}{c} \boldsymbol{\hat{g}}^{\mathcal{D}}\\ \boldsymbol{\hat{g}}^{\mathcal{H}} \end{array}\right] \]](form_270.png)
which will then be solved for the unknown coefficients 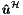 as,
as,
![\[ \boldsymbol{M}^{\mathcal{HH}}\boldsymbol{\hat{u}}^{\mathcal{H}} = \boldsymbol{\hat{f}}^{\mathcal{H}} +\boldsymbol{\hat{g}}^{\mathcal{H}} -\boldsymbol{M}^{\mathcal{HD}}\boldsymbol{\hat{u}}^{\mathcal{D}}\]](form_271.png)
| key | Specifes the linear system to solve. |
| rhs | Forcing term 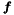 . . |
| inout | Solution vector 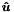 . . |
| dirForcing | . |
Definition at line 335 of file ContField1D.cpp.
References Nektar::SpatialDomains::eDirichlet, GetGlobalLinSys(), Nektar::MultiRegions::DisContField1D::m_bndCondExpansions, Nektar::MultiRegions::DisContField1D::m_bndConditions, m_locToGloMap, and v_ImposeDirichletConditions().
Referenced by FwdTrans(), MultiplyByInvMassMatrix(), and v_HelmSolve().
|
inline |
Scatters from the global coefficients  to the local coefficients
to the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}^{e}[i] = \mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]$ \\ \> \> continue \\ \> continue \end{tabbing}](form_277.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation 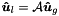 , where
, where 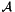 is the
is the 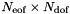 permutation matrix.
permutation matrix.
| inarray | An array of size 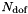 containing the global degrees of freedom containing the global degrees of freedom 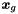 . . |
| outarray | The resulting local degrees of freedom 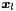 will be stored in this array of size will be stored in this array of size 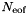 . . |
Definition at line 278 of file ContField1D.h.
References m_locToGloMap.
| void Nektar::MultiRegions::ContField1D::IProductWRTBase | ( | const Array< OneD, const NekDouble > & | inarray, |
| Array< OneD, NekDouble > & | outarray, | ||
| CoeffState | coeffstate = eLocal |
||
| ) |
Calculates the inner product of a function 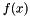 with respect to all global expansion modes
with respect to all global expansion modes 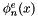 .
.
The operation is evaluated locally (i.e. with respect to all local expansion modes) by the function ExpList::IProductWRTBase. The inner product with respect to the global expansion modes is than obtained by a global assembly operation.
The values of the function 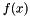 evaluated at the quadrature points
evaluated at the quadrature points 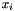 should be contained in the variable m_phys of the ExpList object in. The result is stored in the array m_coeffs.
should be contained in the variable m_phys of the ExpList object in. The result is stored in the array m_coeffs.
| In | An ExpList, containing the discrete evaluation of 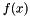 at the quadrature points in its array m_phys. at the quadrature points in its array m_phys. |
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 404 of file ContField1D.cpp.
References Assemble(), Nektar::MultiRegions::eGlobal, Nektar::MultiRegions::ExpList::IProductWRTBase_IterPerExp(), and Nektar::MultiRegions::ExpList::m_ncoeffs.
Referenced by FwdTrans(), v_HelmSolve(), and v_IProductWRTBase().
| void Nektar::MultiRegions::ContField1D::LocalToGlobal | ( | ) |
Gathers the global coefficients  from the local coefficients
from the local coefficients  .
.
Reimplemented from Nektar::MultiRegions::ExpList.
| void Nektar::MultiRegions::ContField1D::MultiplyByInvMassMatrix | ( | const Array< OneD, const NekDouble > & | inarray, |
| Array< OneD, NekDouble > & | outarray, | ||
| CoeffState | coeffstate = eLocal |
||
| ) |
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 250 of file ContField1D.cpp.
References Assemble(), Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eMass, GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), m_locToGloMap, and Nektar::MultiRegions::ExpList::m_ncoeffs.
Referenced by v_MultiplyByInvMassMatrix().
|
privatevirtual |
Definition at line 579 of file ContField1D.cpp.
References BwdTrans().
|
privatevirtual |
|
privatevirtual |
Calculates the result of the multiplication of a global matrix of type specified by mkey with a vector given by inarray.
This is equivalent to the operation:
![\[\boldsymbol{M\hat{u}}_g\]](form_285.png)
where 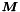 is the global matrix of type specified by mkey. After scattering the global array inarray to local level, this operation is evaluated locally by the function ExpList::GeneralMatrixOp. The global result is then obtained by a global assembly procedure.
is the global matrix of type specified by mkey. After scattering the global array inarray to local level, this operation is evaluated locally by the function ExpList::GeneralMatrixOp. The global result is then obtained by a global assembly procedure.
| mkey | This key uniquely defines the type matrix required for the operation. |
| inarray | The vector  of size of size 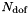 . . |
| outarray | The resulting vector of size 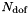 . . |
Definition at line 611 of file ContField1D.cpp.
References Assemble(), Nektar::MultiRegions::eGlobal, Nektar::MultiRegions::ExpList::GeneralMatrixOp_IterPerExp(), Nektar::MultiRegions::ExpList::GlobalToLocal(), and Nektar::MultiRegions::ExpList::m_ncoeffs.
|
privatevirtual |
Definition at line 574 of file ContField1D.cpp.
References GetBndConditions().
Scatters from the global coefficients  to the local coefficients
to the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}^{e}[i] = \mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]$ \\ \> \> continue \\ \> continue \end{tabbing}](form_277.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation 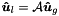 , where
, where 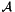 is the
is the 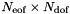 permutation matrix.
permutation matrix.
Definition at line 495 of file ContField1D.cpp.
References Nektar::MultiRegions::ExpList::m_coeffs, and m_locToGloMap.
|
privatevirtual |
Consider the one dimensional Helmholtz equation,
![\[\frac{d^2u}{dx^2}-\lambda u(x) = f(x),\]](form_279.png)
supplemented with appropriate boundary conditions (which are contained in the data member m_bndCondExpansions). Applying a 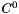 continuous Galerkin discretisation, this equation leads to the following linear system:
continuous Galerkin discretisation, this equation leads to the following linear system:
![\[\left( \boldsymbol{M}+\lambda\boldsymbol{L}\right) \boldsymbol{\hat{u}}_g=\boldsymbol{\hat{f}}\]](form_281.png)
where 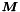 and
and 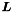 are the mass and Laplacian matrix respectively. This function solves the system above for the global coefficients
are the mass and Laplacian matrix respectively. This function solves the system above for the global coefficients 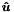 by a call to the function GlobalSolve.
by a call to the function GlobalSolve.
The values of the function 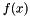 evaluated at the quadrature points
evaluated at the quadrature points 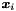 should be contained in the variable m_phys of the ExpList object inarray. The resulting global coefficients
should be contained in the variable m_phys of the ExpList object inarray. The resulting global coefficients  are stored in the array m_coeffs.
are stored in the array m_coeffs.
| inarray | Input containing forcing function 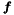 at the quadrature points. at the quadrature points. |
| outarray | Output containing the coefficients 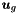 |
| lambda | Parameter value. |
| Sigma | Coefficients of lambda. |
| varcoeff | Variable diffusivity coefficients. |
| coeffstate | |
| dirForcing | Dirichlet Forcing. |
Definition at line 530 of file ContField1D.cpp.
References Nektar::SpatialDomains::eDirichlet, Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eHelmholtz, Nektar::eUseGlobal, GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), IProductWRTBase(), Nektar::FlagList::isSet(), Nektar::MultiRegions::DisContField1D::m_bndCondExpansions, Nektar::MultiRegions::DisContField1D::m_bndConditions, m_locToGloMap, and Vmath::Neg().
|
privatevirtual |
Impose the Dirichlet Boundary Conditions on outarray.
Definition at line 438 of file ContField1D.cpp.
References Nektar::SpatialDomains::eDirichlet, Nektar::MultiRegions::DisContField1D::m_bndCondExpansions, Nektar::MultiRegions::DisContField1D::m_bndConditions, and m_locToGloMap.
Referenced by GlobalSolve().
|
privatevirtual |
Definition at line 587 of file ContField1D.cpp.
References IProductWRTBase().
Gathers the global coefficients  from the local coefficients
from the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}_g[\mbox{map}[e][i]] = \mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}^{e}[i]$\\ \> \> continue\\ \> continue \end{tabbing}](form_272.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation 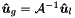 , where
, where 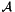 is the
is the 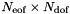 permutation matrix.
permutation matrix.
Definition at line 470 of file ContField1D.cpp.
References Nektar::MultiRegions::ExpList::m_coeffs, and m_locToGloMap.
|
privatevirtual |
Definition at line 430 of file ContField1D.cpp.
References MultiplyByInvMassMatrix().
|
protected |
A enum list declaring how to interpret coeffs, i.e. eLocal, eHybrid or eGlobal.
Definition at line 154 of file ContField1D.h.
|
protected |
A manager which collects all the global linear systems being assembled, such that they should be constructed only once.
Definition at line 164 of file ContField1D.h.
Referenced by GetGlobalLinSys().
|
protected |
(A shared pointer to) a list which collects all the global matrices being assembled, such that they should be constructed only once.
Definition at line 159 of file ContField1D.h.
|
protected |
(A shared pointer to) the object which contains all the required information for the transformation from local to global degrees of freedom.
Definition at line 149 of file ContField1D.h.
Referenced by Assemble(), ContField1D(), FwdTrans(), GenGlobalLinSys(), GetLocalToGlobalMap(), GlobalSolve(), GlobalToLocal(), MultiplyByInvMassMatrix(), v_GlobalToLocal(), v_HelmSolve(), v_ImposeDirichletConditions(), and v_LocalToGlobal().
 1.8.1.2
1.8.1.2