|
Nektar++
|
|
Nektar++
|
This class is the abstraction of a global continuous two- dimensional spectral/hp element expansion which approximates the solution of a set of partial differential equations. More...
#include <ContField2D.h>
Public Member Functions | |
| ContField2D () | |
| The default constructor. | |
| ContField2D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph2D, const std::string &variable="DefaultVar", const bool DeclareCoeffPhysArrays=true, const bool CheckIfSingularSystem=false) | |
| This constructor sets up global continuous field based on an input mesh and boundary conditions. | |
| ContField2D (const ContField2D &In, const SpatialDomains::MeshGraphSharedPtr &graph2D, const std::string &variable, const bool DeclareCoeffPhysArrays=true, const bool CheckIfSingularSystem=false) | |
| Construct a global continuous field with solution type based on another field but using a separate input mesh and boundary conditions. | |
| ContField2D (const ContField2D &In, bool DeclareCoeffPhysArrays=true) | |
| The copy constructor. | |
| virtual | ~ContField2D () |
| The default destructor. | |
| void | GlobalToLocal (Array< OneD, NekDouble > &outarray) const |
Scatters from the global coefficients  to the local coefficients to the local coefficients  . . | |
| void | GlobalToLocal (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) const |
Scatters from the global coefficients  to the local coefficients to the local coefficients  . . | |
| void | LocalToGlobal (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) const |
| void | Assemble () |
Assembles the global coefficients  from the local coefficients from the local coefficients  . . | |
| void | Assemble (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) const |
Assembles the global coefficients  from the local coefficients from the local coefficients  . . | |
| const AssemblyMapCGSharedPtr & | GetLocalToGlobalMap () const |
| Returns the map from local to global level. | |
| void | IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
Calculates the inner product of a function  with respect to all global expansion modes with respect to all global expansion modes 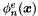 . . | |
| void | FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
Performs the global forward transformation of a function  , subject to the boundary conditions specified. , subject to the boundary conditions specified. | |
| void | BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| Performs the backward transformation of the spectral/hp element expansion. | |
| void | MultiplyByInvMassMatrix (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| Multiply a solution by the inverse mass matrix. | |
| void | LaplaceSolve (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray, const Array< OneD, Array< OneD, NekDouble > > &variablecoeffs=NullNekDoubleArrayofArray, NekDouble time=0.0, CoeffState coeffstate=eLocal) |
| Solves the two-dimensional Laplace equation, subject to the boundary conditions specified. | |
| void | LinearAdvectionEigs (const NekDouble ax, const NekDouble ay, Array< OneD, NekDouble > &Real, Array< OneD, NekDouble > &Imag, Array< OneD, NekDouble > &Evecs=NullNekDouble1DArray) |
| Compute the eigenvalues of the linear advection operator. | |
| const Array< OneD, const MultiRegions::ExpListSharedPtr > & | GetBndCondExpansions () |
| Returns the boundary conditions expansion. | |
| const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > & | GetBndConditions () |
| Returns the boundary conditions. | |
| int | GetGlobalMatrixNnz (const GlobalMatrixKey &gkey) |
 Public Member Functions inherited from Nektar::MultiRegions::DisContField2D Public Member Functions inherited from Nektar::MultiRegions::DisContField2D | |
| DisContField2D () | |
| DisContField2D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph2D, const std::string &variable, const bool SetUpJustDG=true, const bool DeclareCoeffPhysArrays=true) | |
| DisContField2D (const DisContField2D &In, const SpatialDomains::MeshGraphSharedPtr &graph2D, const std::string &variable, const bool SetUpJustDG=false, const bool DeclareCoeffPhysArrays=true) | |
| DisContField2D (const DisContField2D &In, const bool DeclareCoeffPhysArrays=true) | |
| virtual | ~DisContField2D () |
| Default destructor. | |
| GlobalLinSysSharedPtr | GetGlobalBndLinSys (const GlobalLinSysKey &mkey) |
| NekDouble | L2_DGDeriv (const int dir, const Array< OneD, const NekDouble > &soln) |
Calculate the 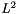 error of the error of the 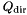 derivative using the consistent DG evaluation of derivative using the consistent DG evaluation of 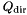 . . | |
| void | EvaluateHDGPostProcessing (Array< OneD, NekDouble > &outarray) |
| Evaluate HDG post-processing to increase polynomial order of solution. | |
| virtual ExpListSharedPtr & | v_GetTrace () |
 Public Member Functions inherited from Nektar::MultiRegions::ExpList2D Public Member Functions inherited from Nektar::MultiRegions::ExpList2D | |
| ExpList2D () | |
| Default constructor. | |
| ExpList2D (const ExpList2D &In, const bool DeclareCoeffPhysArrays=true) | |
| Copy constructor. | |
| ExpList2D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &graph2D, const bool DelcareCoeffPhysArrays=true, const std::string &var="DefaultVar") | |
| Sets up a list of local expansions based on an input mesh. | |
| ExpList2D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::ExpansionMap &expansions, const bool DeclareCoeffPhysArrays=true) | |
| Sets up a list of local expansions based on an expansion Map. | |
| ExpList2D (const LibUtilities::SessionReaderSharedPtr &pSession, const LibUtilities::BasisKey &TriBa, const LibUtilities::BasisKey &TriBb, const LibUtilities::BasisKey &QuadBa, const LibUtilities::BasisKey &QuadBb, const SpatialDomains::MeshGraphSharedPtr &graph2D, const LibUtilities::PointsType TriNb=LibUtilities::SIZE_PointsType) | |
| Sets up a list of local expansions based on an input mesh and separately defined basiskeys. | |
| ExpList2D (const LibUtilities::SessionReaderSharedPtr &pSession, const Array< OneD, const ExpListSharedPtr > &bndConstraint, const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > &bndCond, const LocalRegions::ExpansionVector &locexp, const SpatialDomains::MeshGraphSharedPtr &graph3D, const PeriodicMap &periodicFaces, const bool DeclareCoeffPhysArrays=true, const std::string variable="DefaultVar") | |
| ExpList2D (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::CompositeMap &domain, const SpatialDomains::MeshGraphSharedPtr &graph3D, const std::string variable="DefaultVar") | |
| Specialised constructor for Neumann boundary conditions in DisContField3D and ContField3D. | |
| virtual | ~ExpList2D () |
| Destructor. | |
 Public Member Functions inherited from Nektar::MultiRegions::ExpList Public Member Functions inherited from Nektar::MultiRegions::ExpList | |
| ExpList () | |
| The default constructor. | |
| ExpList (const LibUtilities::SessionReaderSharedPtr &pSession) | |
| The default constructor. | |
| ExpList (const LibUtilities::SessionReaderSharedPtr &pSession, const SpatialDomains::MeshGraphSharedPtr &pGraph) | |
| The default constructor. | |
| ExpList (const ExpList &in, const bool DeclareCoeffPhysArrays=true) | |
| The copy constructor. | |
| virtual | ~ExpList () |
| The default destructor. | |
| int | GetNcoeffs (void) const |
Returns the total number of local degrees of freedom 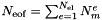 . . | |
| int | GetNcoeffs (const int eid) const |
| Returns the total number of local degrees of freedom for element eid. | |
| ExpansionType | GetExpType (void) |
| Returns the type of the expansion. | |
| void | SetExpType (ExpansionType Type) |
| Returns the type of the expansion. | |
| int | EvalBasisNumModesMax (void) const |
| Evaulates the maximum number of modes in the elemental basis order over all elements. | |
| const Array< OneD, int > | EvalBasisNumModesMaxPerExp (void) const |
| Returns the vector of the number of modes in the elemental basis order over all elements. | |
| int | GetTotPoints (void) const |
Returns the total number of quadrature points m_npoints 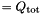 . . | |
| int | GetTotPoints (const int eid) const |
Returns the total number of quadrature points for eid's element 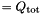 . . | |
| int | GetNpoints (void) const |
Returns the total number of quadrature points m_npoints 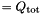 . . | |
| int | Get1DScaledTotPoints (const NekDouble scale) const |
| Returns the total number of qudature points scaled by the factor scale on each 1D direction. | |
| void | SetWaveSpace (const bool wavespace) |
| Sets the wave space to the one of the possible configuration true or false. | |
| void | SetModifiedBasis (const bool modbasis) |
| Set Modified Basis for the stability analysis. | |
| void | SetPhys (int i, NekDouble val) |
| Set the i th value of m_phys to value val. | |
| bool | GetWaveSpace (void) const |
| This function returns the third direction expansion condition, which can be in wave space (coefficient) or not It is stored in the variable m_WaveSpace. | |
| void | SetPhys (const Array< OneD, const NekDouble > &inarray) |
| Fills the array m_phys. | |
| void | SetPhysArray (Array< OneD, NekDouble > &inarray) |
| Sets the array m_phys. | |
| void | SetPhysState (const bool physState) |
This function manually sets whether the array of physical values 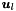 (implemented as m_phys) is filled or not. (implemented as m_phys) is filled or not. | |
| bool | GetPhysState (void) const |
This function indicates whether the array of physical values 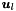 (implemented as m_phys) is filled or not. (implemented as m_phys) is filled or not. | |
| NekDouble | PhysIntegral (void) |
This function integrates a function  over the domain consisting of all the elements of the expansion. over the domain consisting of all the elements of the expansion. | |
| NekDouble | PhysIntegral (const Array< OneD, const NekDouble > &inarray) |
This function integrates a function  over the domain consisting of all the elements of the expansion. over the domain consisting of all the elements of the expansion. | |
| void | IProductWRTBase_IterPerExp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
This function calculates the inner product of a function  with respect to all {local} expansion modes with respect to all {local} expansion modes 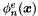 . . | |
| void | IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
This function calculates the inner product of a function  with respect to the derivative (in direction. with respect to the derivative (in direction. | |
| void | FwdTrans_IterPerExp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
This function elementally evaluates the forward transformation of a function 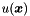 onto the global spectral/hp expansion. onto the global spectral/hp expansion. | |
| void | MultiplyByElmtInvMass (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function elementally mulplies the coefficient space of Sin my the elemental inverse of the mass matrix. | |
| void | SmoothField (Array< OneD, NekDouble > &field) |
| Smooth a field across elements. | |
| void | HelmSolve (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const FlagList &flags, const StdRegions::ConstFactorMap &factors, const StdRegions::VarCoeffMap &varcoeff=StdRegions::NullVarCoeffMap, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solve helmholtz problem. | |
| void | LinearAdvectionDiffusionReactionSolve (const Array< OneD, Array< OneD, NekDouble > > &velocity, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const NekDouble lambda, CoeffState coeffstate=eLocal, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solve Advection Diffusion Reaction. | |
| void | LinearAdvectionReactionSolve (const Array< OneD, Array< OneD, NekDouble > > &velocity, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const NekDouble lambda, CoeffState coeffstate=eLocal, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solve Advection Diffusion Reaction. | |
| void | FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| void | BwdTrans_IterPerExp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function elementally evaluates the backward transformation of the global spectral/hp element expansion. | |
| void | GetCoords (Array< OneD, NekDouble > &coord_0, Array< OneD, NekDouble > &coord_1=NullNekDouble1DArray, Array< OneD, NekDouble > &coord_2=NullNekDouble1DArray) |
This function calculates the coordinates of all the elemental quadrature points 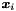 . . | |
| void | HomogeneousFwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal, bool Shuff=true, bool UnShuff=true) |
| void | HomogeneousBwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal, bool Shuff=true, bool UnShuff=true) |
| void | DealiasedProd (const Array< OneD, NekDouble > &inarray1, const Array< OneD, NekDouble > &inarray2, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| void | GetBCValues (Array< OneD, NekDouble > &BndVals, const Array< OneD, NekDouble > &TotField, int BndID) |
| void | NormVectorIProductWRTBase (Array< OneD, const NekDouble > &V1, Array< OneD, const NekDouble > &V2, Array< OneD, NekDouble > &outarray, int BndID) |
| void | ApplyGeomInfo () |
| Apply geometry information to each expansion. | |
| void | WriteTecplotHeader (std::ofstream &outfile, std::string var="") |
| void | WriteTecplotZone (std::ofstream &outfile, int expansion=-1) |
| void | WriteTecplotField (std::ofstream &outfile, int expansion=-1) |
| void | WriteTecplotConnectivity (std::ofstream &outfile, int expansion=-1) |
| void | WriteVtkHeader (std::ofstream &outfile) |
| void | WriteVtkFooter (std::ofstream &outfile) |
| void | WriteVtkPieceHeader (std::ofstream &outfile, int expansion) |
| void | WriteVtkPieceFooter (std::ofstream &outfile, int expansion) |
| void | WriteVtkPieceData (std::ofstream &outfile, int expansion, std::string var="v") |
| int | GetCoordim (int eid) |
| This function returns the dimension of the coordinates of the element eid. | |
| void | SetCoeff (int i, NekDouble val) |
| Set the i th coefficiient in m_coeffs to value val. | |
| void | SetCoeffs (int i, NekDouble val) |
| Set the i th coefficiient in m_coeffs to value val. | |
| void | SetCoeffsArray (Array< OneD, NekDouble > &inarray) |
| Set the m_coeffs array to inarray. | |
| const Array< OneD, const NekDouble > & | GetCoeffs () const |
This function returns (a reference to) the array  (implemented as m_coeffs) containing all local expansion coefficients. (implemented as m_coeffs) containing all local expansion coefficients. | |
| void | ImposeDirichletConditions (Array< OneD, NekDouble > &outarray) |
| Impose Dirichlet Boundary Conditions onto Array. | |
| void | FillBndCondFromField (void) |
| Fill Bnd Condition expansion from the values stored in expansion. | |
| void | LocalToGlobal (void) |
| Put the coefficients into global ordering using m_coeffs. | |
| void | GlobalToLocal (void) |
| Put the coefficients into local ordering and place in m_coeffs. | |
| NekDouble | GetCoeff (int i) |
| Get the i th value (coefficient) of m_coeffs. | |
| NekDouble | GetCoeffs (int i) |
| Get the i th value (coefficient) of m_coeffs. | |
| const Array< OneD, const NekDouble > & | GetPhys () const |
This function returns (a reference to) the array 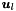 (implemented as m_phys) containing the function (implemented as m_phys) containing the function 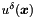 evaluated at the quadrature points. evaluated at the quadrature points. | |
| NekDouble | Linf (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &soln=NullNekDouble1DArray) |
This function calculates the 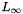 error of the global spectral/hp element approximation. error of the global spectral/hp element approximation. | |
| NekDouble | L2 (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &soln=NullNekDouble1DArray) |
This function calculates the 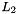 error with respect to soln of the global spectral/hp element approximation. error with respect to soln of the global spectral/hp element approximation. | |
| NekDouble | H1 (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &soln=NullNekDouble1DArray) |
Calculates the 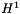 error of the global spectral/hp element approximation. error of the global spectral/hp element approximation. | |
| NekDouble | Integral (const Array< OneD, const NekDouble > &inarray) |
| Array< OneD, const NekDouble > | HomogeneousEnergy (void) |
| This function calculates the energy associated with each one of the modesof a 3D homogeneous nD expansion. | |
| void | SetHomo1DSpecVanVisc (Array< OneD, NekDouble > visc) |
| This function sets the Spectral Vanishing Viscosity in homogeneous1D expansion. | |
| Array< OneD, const unsigned int > | GetZIDs (void) |
| This function returns a vector containing the wave numbers in z-direction associated with the 3D homogenous expansion. Required if a parellelisation is applied in the Fourier direction. | |
| LibUtilities::TranspositionSharedPtr | GetTransposition (void) |
| This function returns the transposition class associaed with the homogeneous expansion. | |
| NekDouble | GetHomoLen (void) |
| This function returns the Width of homogeneous direction associaed with the homogeneous expansion. | |
| Array< OneD, const unsigned int > | GetYIDs (void) |
| This function returns a vector containing the wave numbers in y-direction associated with the 3D homogenous expansion. Required if a parellelisation is applied in the Fourier direction. | |
| void | PhysInterp1DScaled (const NekDouble scale, const Array< OneD, NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function interpolates the physical space points in inarray to outarray using the same points defined in the expansion but where the number of points are rescaled by 1DScale. | |
| void | PhysGalerkinProjection1DScaled (const NekDouble scale, const Array< OneD, NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This function Galerkin projects the physical space points in inarray to outarray where inarray is assumed to be defined in the expansion but where the number of points are rescaled by 1DScale. | |
| int | GetExpSize (void) |
| This function returns the number of elements in the expansion. | |
| int | GetNumElmts (void) |
| This function returns the number of elements in the expansion which may be different for a homogeoenous extended expansionp. | |
| const boost::shared_ptr < LocalRegions::ExpansionVector > | GetExp () const |
| This function returns the vector of elements in the expansion. | |
| LocalRegions::ExpansionSharedPtr & | GetExp (int n) const |
This function returns (a shared pointer to) the local elemental expansion of the 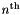 element. element. | |
| LocalRegions::ExpansionSharedPtr & | GetExp (const Array< OneD, const NekDouble > &gloCoord) |
| This function returns (a shared pointer to) the local elemental expansion containing the arbitrary point given by gloCoord. | |
| int | GetExpIndex (const Array< OneD, const NekDouble > &gloCoord, NekDouble tol=0.0, bool returnNearestElmt=false) |
| int | GetExpIndex (const Array< OneD, const NekDouble > &gloCoords, Array< OneD, NekDouble > &locCoords, NekDouble tol=0.0, bool returnNearestElmt=false) |
| int | GetCoeff_Offset (int n) const |
| Get the start offset position for a global list of m_coeffs correspoinding to element n. | |
| int | GetPhys_Offset (int n) const |
| Get the start offset position for a global list of m_phys correspoinding to element n. | |
| int | GetOffset_Elmt_Id (int n) const |
| Get the element id associated with the n th consecutive block of data in m_phys and m_coeffs. | |
| Array< OneD, NekDouble > & | UpdateCoeffs () |
This function returns (a reference to) the array  (implemented as m_coeffs) containing all local expansion coefficients. (implemented as m_coeffs) containing all local expansion coefficients. | |
| Array< OneD, NekDouble > & | UpdatePhys () |
This function returns (a reference to) the array 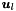 (implemented as m_phys) containing the function (implemented as m_phys) containing the function 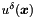 evaluated at the quadrature points. evaluated at the quadrature points. | |
| void | PhysDeriv (Direction edir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d) |
| void | PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray) |
This function discretely evaluates the derivative of a function  on the domain consisting of all elements of the expansion. on the domain consisting of all elements of the expansion. | |
| void | PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d) |
| boost::shared_ptr< ExpList > & | UpdateBndCondExpansion (int i) |
| void | Upwind (const Array< OneD, const Array< OneD, NekDouble > > &Vec, const Array< OneD, const NekDouble > &Fwd, const Array< OneD, const NekDouble > &Bwd, Array< OneD, NekDouble > &Upwind) |
| void | Upwind (const Array< OneD, const NekDouble > &Vn, const Array< OneD, const NekDouble > &Fwd, const Array< OneD, const NekDouble > &Bwd, Array< OneD, NekDouble > &Upwind) |
| boost::shared_ptr< ExpList > & | GetTrace () |
| boost::shared_ptr < AssemblyMapDG > & | GetTraceMap (void) |
| const Array< OneD, const int > & | GetTraceBndMap (void) |
| void | GetNormals (Array< OneD, Array< OneD, NekDouble > > &normals) |
| void | AddTraceIntegral (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray) |
| void | AddTraceIntegral (const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray) |
| void | AddFwdBwdTraceIntegral (const Array< OneD, const NekDouble > &Fwd, const Array< OneD, const NekDouble > &Bwd, Array< OneD, NekDouble > &outarray) |
| void | GetFwdBwdTracePhys (Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| void | GetFwdBwdTracePhys (const Array< OneD, const NekDouble > &field, Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| void | ExtractTracePhys (Array< OneD, NekDouble > &outarray) |
| void | ExtractTracePhys (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| Array< OneD, SpatialDomains::BoundaryConditionShPtr > & | UpdateBndConditions () |
| void | EvaluateBoundaryConditions (const NekDouble time=0.0, const std::string varName="", const NekDouble=NekConstants::kNekUnsetDouble, const NekDouble=NekConstants::kNekUnsetDouble) |
| void | GeneralMatrixOp (const GlobalMatrixKey &gkey, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| This function calculates the result of the multiplication of a matrix of type specified by mkey with a vector given by inarray. | |
| void | GeneralMatrixOp_IterPerExp (const GlobalMatrixKey &gkey, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| void | SetUpPhysNormals () |
| void | GetBoundaryToElmtMap (Array< OneD, int > &ElmtID, Array< OneD, int > &EdgeID) |
| void | GeneralGetFieldDefinitions (std::vector< LibUtilities::FieldDefinitionsSharedPtr > &fielddef, int NumHomoDir=0, Array< OneD, LibUtilities::BasisSharedPtr > &HomoBasis=LibUtilities::NullBasisSharedPtr1DArray, std::vector< NekDouble > &HomoLen=LibUtilities::NullNekDoubleVector, std::vector< unsigned int > &HomoZIDs=LibUtilities::NullUnsignedIntVector, std::vector< unsigned int > &HomoYIDs=LibUtilities::NullUnsignedIntVector) |
| const NekOptimize::GlobalOptParamSharedPtr & | GetGlobalOptParam (void) |
| map< int, RobinBCInfoSharedPtr > | GetRobinBCInfo () |
| void | GetPeriodicEntities (PeriodicMap &periodicVerts, PeriodicMap &periodicEdges, PeriodicMap &periodicFaces=NullPeriodicMap) |
| std::vector < LibUtilities::FieldDefinitionsSharedPtr > | GetFieldDefinitions () |
| void | GetFieldDefinitions (std::vector< LibUtilities::FieldDefinitionsSharedPtr > &fielddef) |
| void | AppendFieldData (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata) |
| Append the element data listed in elements fielddef->m_ElementIDs onto fielddata. | |
| void | AppendFieldData (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata, Array< OneD, NekDouble > &coeffs) |
| Append the data in coeffs listed in elements fielddef->m_ElementIDs onto fielddata. | |
| void | ExtractElmtDataToCoeffs (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata, std::string &field, Array< OneD, NekDouble > &coeffs) |
| Extract the data in fielddata into the coeffs using the basic ExpList Elemental expansions rather than planes in homogeneous case. | |
| void | ExtractCoeffsToCoeffs (const boost::shared_ptr< ExpList > &fromExpList, const Array< OneD, const NekDouble > &fromCoeffs, Array< OneD, NekDouble > &toCoeffs) |
| Extract the data from fromField using fromExpList the coeffs using the basic ExpList Elemental expansions rather than planes in homogeneous case. | |
| void | ExtractDataToCoeffs (LibUtilities::FieldDefinitionsSharedPtr &fielddef, std::vector< NekDouble > &fielddata, std::string &field, Array< OneD, NekDouble > &coeffs) |
| Extract the data in fielddata into the coeffs. | |
| boost::shared_ptr< ExpList > | GetSharedThisPtr () |
| Returns a shared pointer to the current object. | |
| boost::shared_ptr < LibUtilities::SessionReader > | GetSession () |
| Returns the session object. | |
| boost::shared_ptr < LibUtilities::Comm > | GetComm () |
| Returns the comm object. | |
| SpatialDomains::MeshGraphSharedPtr | GetGraph () |
| LibUtilities::BasisSharedPtr | GetHomogeneousBasis (void) |
| boost::shared_ptr< ExpList > & | GetPlane (int n) |
Private Member Functions | |
| void | GlobalSolve (const GlobalLinSysKey &key, const Array< OneD, const NekDouble > &rhs, Array< OneD, NekDouble > &inout, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| Solves the linear system specified by the key key. | |
| GlobalMatrixSharedPtr | GetGlobalMatrix (const GlobalMatrixKey &mkey) |
| Returns the global matrix specified by mkey. | |
| GlobalLinSysSharedPtr | GetGlobalLinSys (const GlobalLinSysKey &mkey) |
| Returns the linear system specified by the key mkey. | |
| GlobalLinSysSharedPtr | GenGlobalLinSys (const GlobalLinSysKey &mkey) |
| virtual void | v_ImposeDirichletConditions (Array< OneD, NekDouble > &outarray) |
| Impose the Dirichlet Boundary Conditions on outarray. | |
| virtual void | v_FillBndCondFromField () |
| virtual void | v_LocalToGlobal (void) |
Gathers the global coefficients  from the local coefficients from the local coefficients  . . | |
| virtual void | v_GlobalToLocal (void) |
Scatters from the global coefficients  to the local coefficients to the local coefficients  . . | |
| virtual void | v_BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| Template method virtual forwarder for FwdTrans(). | |
| virtual void | v_FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| Template method virtual forwarder for FwdTrans(). | |
| virtual void | v_SmoothField (Array< OneD, NekDouble > &field) |
| Template method virtual forwarded for SmoothField(). | |
| virtual void | v_MultiplyByInvMassMatrix (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| Template method virtual forwarder for MultiplyByInvMassMatrix(). | |
| virtual void | v_HelmSolve (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const FlagList &flags, const StdRegions::ConstFactorMap &factors, const StdRegions::VarCoeffMap &varcoeff, const Array< OneD, const NekDouble > &dirForcing) |
| Solves the two-dimensional Helmholtz equation, subject to the boundary conditions specified. | |
| virtual void | v_GeneralMatrixOp (const GlobalMatrixKey &gkey, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate) |
| Calculates the result of the multiplication of a global matrix of type specified by mkey with a vector given by inarray. | |
| virtual void | v_LinearAdvectionDiffusionReactionSolve (const Array< OneD, Array< OneD, NekDouble > > &velocity, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const NekDouble lambda, CoeffState coeffstate=eLocal, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| void | v_LinearAdvectionReactionSolve (const Array< OneD, Array< OneD, NekDouble > > &velocity, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const NekDouble lambda, CoeffState coeffstate=eLocal, const Array< OneD, const NekDouble > &dirForcing=NullNekDouble1DArray) |
| virtual const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > & | v_GetBndConditions () |
| Template method virtual forwarder for GetBndConditions(). | |
Private Attributes | |
| AssemblyMapCGSharedPtr | m_locToGloMap |
| (A shared pointer to) the object which contains all the required information for the transformation from local to global degrees of freedom. | |
| GlobalMatrixMapShPtr | m_globalMat |
| (A shared pointer to) a list which collects all the global matrices being assembled, such that they should be constructed only once. | |
| LibUtilities::NekManager < GlobalLinSysKey, GlobalLinSys > | m_globalLinSysManager |
| A manager which collects all the global linear systems being assembled, such that they should be constructed only once. | |
Additional Inherited Members | |
 Public Attributes inherited from Nektar::MultiRegions::ExpList Public Attributes inherited from Nektar::MultiRegions::ExpList | |
| ExpansionType | m_expType |
 Protected Member Functions inherited from Nektar::MultiRegions::DisContField2D Protected Member Functions inherited from Nektar::MultiRegions::DisContField2D | |
| void | SetUpDG (const std::string="DefaultVar") |
| Set up all DG member variables and maps. | |
| bool | SameTypeOfBoundaryConditions (const DisContField2D &In) |
| void | GenerateBoundaryConditionExpansion (const SpatialDomains::MeshGraphSharedPtr &graph2D, const SpatialDomains::BoundaryConditions &bcs, const std::string &variable, const bool DeclareCoeffPhysArrays=true) |
| This function discretises the boundary conditions by setting up a list of one-dimensional boundary expansions. | |
| void | FindPeriodicEdges (const SpatialDomains::BoundaryConditions &bcs, const std::string &variable) |
| Determine the periodic edges and vertices for the given graph. | |
| bool | IsLeftAdjacentEdge (const int n, const int e) |
| virtual void | v_GetFwdBwdTracePhys (const Array< OneD, const NekDouble > &field, Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| This method extracts the "forward" and "backward" trace data from the array field and puts the data into output vectors Fwd and Bwd. | |
| virtual void | v_GetFwdBwdTracePhys (Array< OneD, NekDouble > &Fwd, Array< OneD, NekDouble > &Bwd) |
| virtual void | v_AddTraceIntegral (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray) |
| virtual void | v_AddTraceIntegral (const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray) |
| Add trace contributions into elemental coefficient spaces. | |
| virtual void | v_AddFwdBwdTraceIntegral (const Array< OneD, const NekDouble > &Fwd, const Array< OneD, const NekDouble > &Bwd, Array< OneD, NekDouble > &outarray) |
| Add trace contributions into elemental coefficient spaces. | |
| virtual void | v_ExtractTracePhys (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray) |
| This method extracts the trace (edges in 2D) from the field inarray and puts the values in outarray. | |
| virtual void | v_ExtractTracePhys (Array< OneD, NekDouble > &outarray) |
| virtual void | v_FillBndCondFromField () |
| virtual void | v_HelmSolve (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const FlagList &flags, const StdRegions::ConstFactorMap &factors, const StdRegions::VarCoeffMap &varcoeff, const Array< OneD, const NekDouble > &dirForcing) |
| virtual void | v_GeneralMatrixOp (const GlobalMatrixKey &gkey, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, CoeffState coeffstate=eLocal) |
| Calculates the result of the multiplication of a global matrix of type specified by mkey with a vector given by inarray. | |
| virtual void | v_GetBoundaryToElmtMap (Array< OneD, int > &ElmtID, Array< OneD, int > &EdgeID) |
| Set up a list of element IDs and edge IDs that link to the boundary conditions. | |
| virtual void | v_GetPeriodicEntities (PeriodicMap &periodicVerts, PeriodicMap &periodicEdges, PeriodicMap &periodicFaces) |
| Obtain a copy of the periodic edges and vertices for this field. | |
| virtual AssemblyMapDGSharedPtr & | v_GetTraceMap () |
| virtual const Array< OneD, const MultiRegions::ExpListSharedPtr > & | v_GetBndCondExpansions () |
| virtual const Array< OneD, const SpatialDomains::BoundaryConditionShPtr > & | v_GetBndConditions () |
| virtual MultiRegions::ExpListSharedPtr & | v_UpdateBndCondExpansion (int i) |
| virtual Array< OneD, SpatialDomains::BoundaryConditionShPtr > & | v_UpdateBndConditions () |
| virtual void | v_EvaluateBoundaryConditions (const NekDouble time=0.0, const std::string varName="", const NekDouble x2_in=NekConstants::kNekUnsetDouble, const NekDouble x3_in=NekConstants::kNekUnsetDouble) |
| virtual map< int, RobinBCInfoSharedPtr > | v_GetRobinBCInfo () |
| Search through the edge expansions and identify which ones have Robin/Mixed type boundary conditions. | |
 Static Protected Member Functions inherited from Nektar::MultiRegions::ExpList Static Protected Member Functions inherited from Nektar::MultiRegions::ExpList | |
| static SpatialDomains::BoundaryConditionShPtr | GetBoundaryCondition (const SpatialDomains::BoundaryConditionCollection &collection, unsigned int index, const std::string &variable) |
 Protected Attributes inherited from Nektar::MultiRegions::DisContField2D Protected Attributes inherited from Nektar::MultiRegions::DisContField2D | |
| Array< OneD, MultiRegions::ExpListSharedPtr > | m_bndCondExpansions |
| An object which contains the discretised boundary conditions. | |
| Array< OneD, SpatialDomains::BoundaryConditionShPtr > | m_bndConditions |
| An array which contains the information about the boundary condition on the different boundary regions. | |
| GlobalLinSysMapShPtr | m_globalBndMat |
| ExpListSharedPtr | m_trace |
| AssemblyMapDGSharedPtr | m_traceMap |
| Array< OneD, Array< OneD, unsigned int > > | m_mapEdgeToElmn |
| Array< OneD, Array< OneD, unsigned int > > | m_signEdgeToElmn |
| Array< OneD, StdRegions::Orientation > | m_edgedir |
| std::set< int > | m_boundaryEdges |
| A set storing the global IDs of any boundary edges. | |
| PeriodicMap | m_periodicVerts |
| A map which identifies groups of periodic vertices. | |
| PeriodicMap | m_periodicEdges |
| A map which identifies pairs of periodic edges. | |
| vector< int > | m_periodicFwdCopy |
| A vector indicating degress of freedom which need to be copied from forwards to backwards space in case of a periodic boundary condition. | |
| vector< int > | m_periodicBwdCopy |
| vector< bool > | m_leftAdjacentEdges |
This class is the abstraction of a global continuous two- dimensional spectral/hp element expansion which approximates the solution of a set of partial differential equations.
The class ContField2D is able to incorporate the boundary conditions imposed to the problem to be solved. Therefore, the class is equipped with three additional data members:
The first data structure, m_bndCondExpansions, contains the one-dimensional spectral/hp expansion on the boundary, #m_bndTypes stores information about the type of boundary condition on the different parts of the boundary while #m_bndCondEquations holds the equation of the imposed boundary conditions.
Furthermore, in case of Dirichlet boundary conditions, this class is capable of lifting a known solution satisfying these boundary conditions. If we denote the unknown solution by 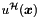 and the known Dirichlet boundary conditions by
and the known Dirichlet boundary conditions by 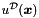 , the expansion then can be decomposed as
, the expansion then can be decomposed as
![\[ u^{\delta}(\boldsymbol{x}_i)=u^{\mathcal{D}}(\boldsymbol{x}_i)+ u^{\mathcal{H}}(\boldsymbol{x}_i)=\sum_{n=0}^{N^{\mathcal{D}}-1} \hat{u}_n^{\mathcal{D}}\Phi_n(\boldsymbol{x}_i)+ \sum_{n={N^{\mathcal{D}}}}^{N_{\mathrm{dof}}-1} \hat{u}_n^{\mathcal{H}} \Phi_n(\boldsymbol{x}_i).\]](form_295.png)
This lifting is accomplished by ordering the known global degrees of freedom, prescribed by the Dirichlet boundary conditions, first in the global array 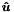 , that is,
, that is,
![\[\boldsymbol{\hat{u}}=\left[ \begin{array}{c} \boldsymbol{\hat{u}}^{\mathcal{D}}\\ \boldsymbol{\hat{u}}^{\mathcal{H}} \end{array} \right].\]](form_254.png)
Such kind of expansions are also referred to as continuous fields. This class should be used when solving 2D problems using a standard Galerkin approach.
Definition at line 56 of file ContField2D.h.
| Nektar::MultiRegions::ContField2D::ContField2D | ( | ) |
The default constructor.
Definition at line 86 of file ContField2D.cpp.
| Nektar::MultiRegions::ContField2D::ContField2D | ( | const LibUtilities::SessionReaderSharedPtr & | pSession, |
| const SpatialDomains::MeshGraphSharedPtr & | graph2D, | ||
| const std::string & | variable = "DefaultVar", |
||
| const bool | DeclareCoeffPhysArrays = true, |
||
| const bool | CheckIfSingularSystem = false |
||
| ) |
This constructor sets up global continuous field based on an input mesh and boundary conditions.
Given a mesh graph2D, containing information about the domain and the spectral/hp element expansion, this constructor fills the list of local expansions m_exp with the proper expansions, calculates the total number of quadrature points 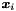 and local expansion coefficients
and local expansion coefficients 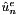 and allocates memory for the arrays m_coeffs and m_phys. Furthermore, it constructs the mapping array (contained in m_locToGloMap) for the transformation between local elemental level and global level, it calculates the total number global expansion coefficients
and allocates memory for the arrays m_coeffs and m_phys. Furthermore, it constructs the mapping array (contained in m_locToGloMap) for the transformation between local elemental level and global level, it calculates the total number global expansion coefficients 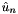 and allocates memory for the array #m_contCoeffs. The constructor also discretises the boundary conditions, specified by the argument bcs, by expressing them in terms of the coefficient of the expansion on the boundary.
and allocates memory for the array #m_contCoeffs. The constructor also discretises the boundary conditions, specified by the argument bcs, by expressing them in terms of the coefficient of the expansion on the boundary.
| graph2D | A mesh, containing information about the domain and the spectral/hp element expansion. |
| bcs | The boundary conditions. |
| variable | An optional parameter to indicate for which variable the field should be constructed. |
Definition at line 118 of file ContField2D.cpp.
References Nektar::MultiRegions::DisContField2D::m_bndCondExpansions, Nektar::MultiRegions::DisContField2D::m_bndConditions, m_locToGloMap, Nektar::MultiRegions::ExpList::m_ncoeffs, Nektar::MultiRegions::DisContField2D::m_periodicEdges, Nektar::MultiRegions::DisContField2D::m_periodicVerts, and Nektar::MultiRegions::ExpList::m_session.
| Nektar::MultiRegions::ContField2D::ContField2D | ( | const ContField2D & | In, |
| const SpatialDomains::MeshGraphSharedPtr & | graph2D, | ||
| const std::string & | variable, | ||
| const bool | DeclareCoeffPhysArrays = true, |
||
| const bool | CheckIfSingularSystem = false |
||
| ) |
Construct a global continuous field with solution type based on another field but using a separate input mesh and boundary conditions.
Given a mesh graph2D, containing information about the domain and the spectral/hp element expansion, this constructor fills the list of local expansions m_exp with the proper expansions, calculates the total number of quadrature points 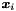 and local expansion coefficients
and local expansion coefficients 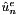 and allocates memory for the arrays m_coeffs and m_phys. Furthermore, it constructs the mapping array (contained in m_locToGloMap) for the transformation between local elemental level and global level, it calculates the total number global expansion coefficients
and allocates memory for the arrays m_coeffs and m_phys. Furthermore, it constructs the mapping array (contained in m_locToGloMap) for the transformation between local elemental level and global level, it calculates the total number global expansion coefficients 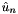 and allocates memory for the array m_coeffs. The constructor also discretises the boundary conditions, specified by the argument bcs, by expressing them in terms of the coefficient of the expansion on the boundary.
and allocates memory for the array m_coeffs. The constructor also discretises the boundary conditions, specified by the argument bcs, by expressing them in terms of the coefficient of the expansion on the boundary.
| In | Existing ContField2D object used to provide the local to global mapping information and global solution type. |
| graph2D | A mesh, containing information about the domain and the spectral/hp element expansion. |
| bcs | The boundary conditions. |
| bc_loc |
Definition at line 168 of file ContField2D.cpp.
References Nektar::MultiRegions::DisContField2D::m_bndCondExpansions, Nektar::MultiRegions::DisContField2D::m_bndConditions, m_locToGloMap, Nektar::MultiRegions::ExpList::m_ncoeffs, Nektar::MultiRegions::DisContField2D::m_periodicEdges, Nektar::MultiRegions::DisContField2D::m_periodicVerts, Nektar::MultiRegions::ExpList::m_session, and Nektar::MultiRegions::DisContField2D::SameTypeOfBoundaryConditions().
| Nektar::MultiRegions::ContField2D::ContField2D | ( | const ContField2D & | In, |
| bool | DeclareCoeffPhysArrays = true |
||
| ) |
The copy constructor.
Initialises the object as a copy of an existing ContField2D object.
| In | Existing ContField2D object. |
| DeclareCoeffPhysArrays | bool to declare if m_phys and m_coeffs should be declared. Default is true |
Definition at line 207 of file ContField2D.cpp.
|
virtual |
|
inline |
Assembles the global coefficients  from the local coefficients
from the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}_g[\mbox{map}[e][i]] = \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]+\mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}^{e}[i]$\\ \> \> continue\\ \> continue \end{tabbing}](form_291.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation 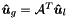 , where
, where 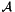 is the
is the 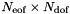 permutation matrix.
permutation matrix.
 and that the resulting global coefficients
and that the resulting global coefficients  will be stored in m_coeffs.
will be stored in m_coeffs. Definition at line 390 of file ContField2D.h.
References Nektar::MultiRegions::ExpList::m_coeffs, and m_locToGloMap.
Referenced by IProductWRTBase(), MultiplyByInvMassMatrix(), and v_GeneralMatrixOp().
|
inline |
Assembles the global coefficients  from the local coefficients
from the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}_g[\mbox{map}[e][i]] = \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]+\mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}^{e}[i]$\\ \> \> continue\\ \> continue \end{tabbing}](form_291.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation 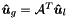 , where
, where 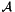 is the
is the 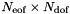 permutation matrix.
permutation matrix.
| inarray | An array of size 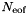 containing the local degrees of freedom containing the local degrees of freedom 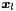 . . |
| outarray | The resulting global degrees of freedom 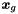 will be stored in this array of size will be stored in this array of size 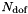 . . |
Definition at line 422 of file ContField2D.h.
References m_locToGloMap.
|
inline |
Performs the backward transformation of the spectral/hp element expansion.
Given the coefficients of an expansion, this function evaluates the spectral/hp expansion 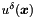 at the quadrature points
at the quadrature points 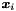 . This operation is evaluated locally by the function ExpList::BwdTrans.
. This operation is evaluated locally by the function ExpList::BwdTrans.
The coefficients of the expansion should be contained in the variable m_coeffs of the ExpList object In. The resulting physical values at the quadrature points 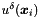 are stored in the array m_phys.
are stored in the array m_phys.
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 498 of file ContField2D.h.
References Nektar::MultiRegions::ExpList::BwdTrans_IterPerExp(), Nektar::StdRegions::eBwdTrans, Nektar::MultiRegions::eGlobal, GetGlobalMatrix(), Nektar::MultiRegions::ExpList::GlobalToLocal(), Nektar::MultiRegions::ExpList::m_globalOptParam, m_locToGloMap, and Nektar::MultiRegions::ExpList::m_ncoeffs.
Referenced by v_BwdTrans(), and v_SmoothField().
| void Nektar::MultiRegions::ContField2D::FwdTrans | ( | const Array< OneD, const NekDouble > & | inarray, |
| Array< OneD, NekDouble > & | outarray, | ||
| CoeffState | coeffstate = eLocal |
||
| ) |
Performs the global forward transformation of a function  , subject to the boundary conditions specified.
, subject to the boundary conditions specified.
Given a function  defined at the quadrature points, this function determines the unknown global coefficients
defined at the quadrature points, this function determines the unknown global coefficients 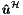 employing a discrete Galerkin projection from physical space to coefficient space. The operation is evaluated by the function GlobalSolve using the global mass matrix.
employing a discrete Galerkin projection from physical space to coefficient space. The operation is evaluated by the function GlobalSolve using the global mass matrix.
The values of the function  evaluated at the quadrature points
evaluated at the quadrature points 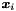 should be contained in the variable m_phys of the ExpList object Sin. The resulting global coefficients
should be contained in the variable m_phys of the ExpList object Sin. The resulting global coefficients 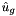 are stored in the array m_coeffs.
are stored in the array m_coeffs.
| Sin | An ExpList, containing the discrete evaluation of  at the quadrature points in its array m_phys. at the quadrature points in its array m_phys. |
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 241 of file ContField2D.cpp.
References Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eMass, GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), IProductWRTBase(), and m_locToGloMap.
Referenced by v_FwdTrans().
|
private |
Definition at line 598 of file ContField2D.cpp.
References ASSERTL1, Nektar::MultiRegions::GlobalMatrixKey::LocToGloMapIsDefined(), and m_locToGloMap.
|
inline |
Returns the boundary conditions expansion.
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 528 of file ContField2D.h.
References Nektar::MultiRegions::DisContField2D::m_bndCondExpansions.
|
inline |
Returns the boundary conditions.
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 534 of file ContField2D.h.
References Nektar::MultiRegions::DisContField2D::m_bndConditions.
Referenced by v_GetBndConditions().
|
private |
Returns the linear system specified by the key mkey.
The function searches the map #m_globalLinSys to see if the global matrix has been created before. If not, it calls the function GenGlobalLinSys to generate the requested global system.
| mkey | This key uniquely defines the requested linear system. |
Definition at line 592 of file ContField2D.cpp.
References m_globalLinSysManager.
Referenced by GlobalSolve().
|
private |
Returns the global matrix specified by mkey.
Returns the global matrix associated with the given GlobalMatrixKey. If the global matrix has not yet been constructed on this field, it is first constructed using GenGlobalMatrix().
| mkey | Global matrix key. |
Definition at line 560 of file ContField2D.cpp.
References ASSERTL1, Nektar::MultiRegions::ExpList::GenGlobalMatrix(), Nektar::iterator, Nektar::MultiRegions::GlobalMatrixKey::LocToGloMapIsDefined(), m_globalMat, and m_locToGloMap.
Referenced by BwdTrans(), IProductWRTBase(), and v_GeneralMatrixOp().
|
inline |
Definition at line 539 of file ContField2D.h.
References ASSERTL1, Nektar::iterator, Nektar::MultiRegions::GlobalMatrixKey::LocToGloMapIsDefined(), and m_globalMat.
|
inline |
Returns the map from local to global level.
Definition at line 431 of file ContField2D.h.
References m_locToGloMap.
|
private |
Solves the linear system specified by the key key.
Given a linear system specified by the key key,
![\[\boldsymbol{M}\boldsymbol{\hat{u}}_g=\boldsymbol{\hat{f}},\]](form_265.png)
this function solves this linear system taking into account the boundary conditions specified in the data member m_bndCondExpansions. Therefore, it adds an array 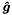 which represents the non-zero surface integral resulting from the weak boundary conditions (e.g. Neumann boundary conditions) to the right hand side, that is,
which represents the non-zero surface integral resulting from the weak boundary conditions (e.g. Neumann boundary conditions) to the right hand side, that is,
![\[\boldsymbol{M}\boldsymbol{\hat{u}}_g=\boldsymbol{\hat{f}}+ \boldsymbol{\hat{g}}.\]](form_267.png)
Furthermore, it lifts the known degrees of freedom which are prescribed by the Dirichlet boundary conditions. As these known coefficients 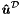 are numbered first in the global coefficient array
are numbered first in the global coefficient array  , the linear system can be decomposed as,
, the linear system can be decomposed as,
![\[\left[\begin{array}{cc} \boldsymbol{M}^{\mathcal{DD}}&\boldsymbol{M}^{\mathcal{DH}}\\ \boldsymbol{M}^{\mathcal{HD}}&\boldsymbol{M}^{\mathcal{HH}} \end{array}\right] \left[\begin{array}{c} \boldsymbol{\hat{u}}^{\mathcal{D}}\\ \boldsymbol{\hat{u}}^{\mathcal{H}} \end{array}\right]= \left[\begin{array}{c} \boldsymbol{\hat{f}}^{\mathcal{D}}\\ \boldsymbol{\hat{f}}^{\mathcal{H}} \end{array}\right]+ \left[\begin{array}{c} \boldsymbol{\hat{g}}^{\mathcal{D}}\\ \boldsymbol{\hat{g}}^{\mathcal{H}} \end{array}\right] \]](form_270.png)
which will then be solved for the unknown coefficients 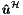 as,
as,
![\[ \boldsymbol{M}^{\mathcal{HH}}\boldsymbol{\hat{u}}^{\mathcal{H}}= \boldsymbol{\hat{f}}^{\mathcal{H}}+ \boldsymbol{\hat{g}}^{\mathcal{H}}- \boldsymbol{M}^{\mathcal{HD}}\boldsymbol{\hat{u}}^{\mathcal{D}}\]](form_306.png)
| mkey | This key uniquely defines the linear system to be solved. |
| Sin | An ExpList, containing the discrete evaluation of the forcing function  at the quadrature points in its array m_phys. at the quadrature points in its array m_phys. |
| ScaleForcing | An optional parameter with which the forcing vector 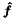 should be multiplied. should be multiplied. |
Definition at line 531 of file ContField2D.cpp.
References GetGlobalLinSys(), m_locToGloMap, and v_ImposeDirichletConditions().
Referenced by FwdTrans(), LaplaceSolve(), MultiplyByInvMassMatrix(), v_HelmSolve(), v_LinearAdvectionDiffusionReactionSolve(), and v_LinearAdvectionReactionSolve().
|
inline |
Scatters from the global coefficients  to the local coefficients
to the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}^{e}[i] = \mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]$ \\ \> \> continue \\ \> continue \end{tabbing}](form_277.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation 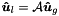 , where
, where 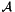 is the
is the 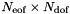 permutation matrix.
permutation matrix.
| outarray | The resulting local degrees of freedom 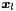 will be stored in this array of size will be stored in this array of size 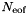 . . |
Definition at line 318 of file ContField2D.h.
References Nektar::MultiRegions::ExpList::m_coeffs, and m_locToGloMap.
|
inline |
Scatters from the global coefficients  to the local coefficients
to the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}^{e}[i] = \mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]$ \\ \> \> continue \\ \> continue \end{tabbing}](form_277.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation 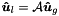 , where
, where 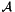 is the
is the 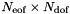 permutation matrix.
permutation matrix.
| inarray | An array of size 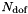 containing the global degrees of freedom containing the global degrees of freedom 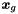 . . |
| outarray | The resulting local degrees of freedom 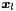 will be stored in this array of size will be stored in this array of size 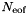 . . |
Definition at line 351 of file ContField2D.h.
References m_locToGloMap.
|
inline |
Calculates the inner product of a function  with respect to all global expansion modes
with respect to all global expansion modes 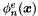 .
.
The operation is evaluated locally (i.e. with respect to all local expansion modes) by the function ExpList::IProductWRTBase. The inner product with respect to the global expansion modes is than obtained by a global assembly operation.
The values of the function  evaluated at the quadrature points
evaluated at the quadrature points 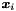 should be contained in the variable m_phys of the ExpList object in. The result is stored in the array m_coeffs.
should be contained in the variable m_phys of the ExpList object in. The result is stored in the array m_coeffs.
| In | An ExpList, containing the discrete evaluation of  at the quadrature points in its array m_phys. at the quadrature points in its array m_phys. |
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 452 of file ContField2D.h.
References Assemble(), Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eIProductWRTBase, GetGlobalMatrix(), Nektar::MultiRegions::ExpList::IProductWRTBase_IterPerExp(), Nektar::MultiRegions::ExpList::m_globalOptParam, m_locToGloMap, and Nektar::MultiRegions::ExpList::m_ncoeffs.
Referenced by FwdTrans(), LaplaceSolve(), v_HelmSolve(), v_LinearAdvectionDiffusionReactionSolve(), v_LinearAdvectionReactionSolve(), and v_SmoothField().
| void Nektar::MultiRegions::ContField2D::LaplaceSolve | ( | const Array< OneD, const NekDouble > & | inarray, |
| Array< OneD, NekDouble > & | outarray, | ||
| const Array< OneD, const NekDouble > & | dirForcing = NullNekDouble1DArray, |
||
| const Array< OneD, Array< OneD, NekDouble > > & | variablecoeffs = NullNekDoubleArrayofArray, |
||
| NekDouble | time = 0.0, |
||
| CoeffState | coeffstate = eLocal |
||
| ) |
Solves the two-dimensional Laplace equation, subject to the boundary conditions specified.
Consider the two dimensional Laplace equation,
![\[\nabla\cdot\left(\boldsymbol{\sigma}\nabla u(\boldsymbol{x})\right) = f(\boldsymbol{x}),\]](form_300.png)
supplemented with appropriate boundary conditions (which are contained in the data member m_bndCondExpansions). In the equation above 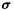 is the (symmetric positive definite) diffusion tensor:
is the (symmetric positive definite) diffusion tensor:
![\[ \sigma = \left[ \begin{array}{cc} \sigma_{00}(\boldsymbol{x},t) & \sigma_{01}(\boldsymbol{x},t) \\ \sigma_{01}(\boldsymbol{x},t) & \sigma_{11}(\boldsymbol{x},t) \end{array} \right]. \]](form_302.png)
Applying a 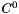 continuous Galerkin discretisation, this equation leads to the following linear system:
continuous Galerkin discretisation, this equation leads to the following linear system:
![\[\boldsymbol{L} \boldsymbol{\hat{u}}_g=\boldsymbol{\hat{f}}\]](form_303.png)
where 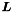 is the Laplacian matrix. This function solves the system above for the global coefficients
is the Laplacian matrix. This function solves the system above for the global coefficients 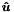 by a call to the function GlobalSolve.
by a call to the function GlobalSolve.
The values of the function  evaluated at the quadrature points
evaluated at the quadrature points 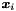 should be contained in the variable m_phys of the ExpList object Sin. The resulting global coefficients
should be contained in the variable m_phys of the ExpList object Sin. The resulting global coefficients  are stored in the array m_coeffs.
are stored in the array m_coeffs.
| Sin | An ExpList, containing the discrete evaluation of the forcing function  at the quadrature points in its array m_phys. at the quadrature points in its array m_phys. |
| variablecoeffs | The (optional) parameter containing the coefficients evaluated at the quadrature points. It is an Array of (three) arrays which stores the laplacian coefficients in the following way
|
| time | The time-level at which the coefficients are evaluated |
Definition at line 382 of file ContField2D.cpp.
References Nektar::SpatialDomains::eDirichlet, Nektar::StdRegions::eFactorTime, Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eLaplacian, Nektar::StdRegions::eVarCoeffD00, Nektar::StdRegions::eVarCoeffD11, Nektar::StdRegions::eVarCoeffD22, Nektar::MultiRegions::ExpList::GetNcoeffs(), GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), IProductWRTBase(), Nektar::MultiRegions::DisContField2D::m_bndCondExpansions, Nektar::MultiRegions::DisContField2D::m_bndConditions, m_locToGloMap, Nektar::MultiRegions::ExpList::m_ncoeffs, and Vmath::Neg().
| void Nektar::MultiRegions::ContField2D::LinearAdvectionEigs | ( | const NekDouble | ax, |
| const NekDouble | ay, | ||
| Array< OneD, NekDouble > & | Real, | ||
| Array< OneD, NekDouble > & | Imag, | ||
| Array< OneD, NekDouble > & | Evecs = NullNekDouble1DArray |
||
| ) |
Compute the eigenvalues of the linear advection operator.
Constructs the GlobalLinearSysKey for the linear advection operator with the supplied parameters, and computes the eigenvectors and eigenvalues of the associated matrix.
| ax | Advection parameter, x. |
| ay | Advection parameter, y. |
| Real | Computed eigenvalues, real component. |
| Imag | Computed eigenvalues, imag component. |
| Evecs | Computed eigenvectors. |
Definition at line 452 of file ContField2D.cpp.
References Nektar::StdRegions::eFactorTime, Nektar::StdRegions::eLinearAdvectionReaction, Nektar::StdRegions::eVarCoeffVelX, Nektar::StdRegions::eVarCoeffVelY, Nektar::MultiRegions::ExpList::GenGlobalMatrixFull(), m_locToGloMap, and Nektar::MultiRegions::ExpList::m_npoints.
|
inline |
Definition at line 358 of file ContField2D.h.
References m_locToGloMap.
| void Nektar::MultiRegions::ContField2D::MultiplyByInvMassMatrix | ( | const Array< OneD, const NekDouble > & | inarray, |
| Array< OneD, NekDouble > & | outarray, | ||
| CoeffState | coeffstate = eLocal |
||
| ) |
Multiply a solution by the inverse mass matrix.
Computes the matrix vector product 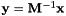 . If coeffstate == eGlobal is set then the elemental system is used directly. If not set, the global system is assembled, the system is solved, and mapped back to the local elemental system.
. If coeffstate == eGlobal is set then the elemental system is used directly. If not set, the global system is assembled, the system is solved, and mapped back to the local elemental system.
| inarray | Input vector 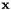 . . |
| outarray | Output vector 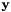 . . |
| coeffState | Flag for using global system. |
Reimplemented from Nektar::MultiRegions::ExpList.
Definition at line 292 of file ContField2D.cpp.
References Assemble(), Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eMass, GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), m_locToGloMap, and Vmath::Vcopy().
Referenced by v_MultiplyByInvMassMatrix(), and v_SmoothField().
|
privatevirtual |
Template method virtual forwarder for FwdTrans().
Definition at line 611 of file ContField2D.cpp.
References BwdTrans().
Definition at line 690 of file ContField2D.cpp.
References Nektar::MultiRegions::ExpList::GetNcoeffs(), Nektar::MultiRegions::ExpList::LocalToGlobal(), Nektar::MultiRegions::DisContField2D::m_bndCondExpansions, Nektar::MultiRegions::ExpList::m_coeffs, m_locToGloMap, and sign.
|
privatevirtual |
Template method virtual forwarder for FwdTrans().
Definition at line 623 of file ContField2D.cpp.
References FwdTrans().
|
privatevirtual |
Calculates the result of the multiplication of a global matrix of type specified by mkey with a vector given by inarray.
This is equivalent to the operation:
![\[\boldsymbol{M\hat{u}}_g\]](form_285.png)
where 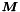 is the global matrix of type specified by mkey. After scattering the global array inarray to local level, this operation is evaluated locally by the function ExpList::GeneralMatrixOp. The global result is then obtained by a global assembly procedure.
is the global matrix of type specified by mkey. After scattering the global array inarray to local level, this operation is evaluated locally by the function ExpList::GeneralMatrixOp. The global result is then obtained by a global assembly procedure.
| mkey | This key uniquely defines the type matrix required for the operation. |
| inarray | The vector  of size of size 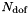 . . |
| outarray | The resulting vector of size 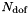 . . |
Definition at line 892 of file ContField2D.cpp.
References Assemble(), Nektar::MultiRegions::eGlobal, Nektar::MultiRegions::ExpList::GeneralMatrixOp_IterPerExp(), GetGlobalMatrix(), Nektar::MultiRegions::GlobalMatrixKey::GetMatrixType(), Nektar::MultiRegions::ExpList::GlobalToLocal(), Nektar::MultiRegions::ExpList::m_globalOptParam, m_locToGloMap, and Nektar::MultiRegions::ExpList::m_ncoeffs.
|
privatevirtual |
Template method virtual forwarder for GetBndConditions().
Definition at line 1042 of file ContField2D.cpp.
References GetBndConditions().
Scatters from the global coefficients  to the local coefficients
to the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}^{e}[i] = \mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}_g[\mbox{map}[e][i]]$ \\ \> \> continue \\ \> continue \end{tabbing}](form_277.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the scatter operation 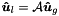 , where
, where 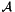 is the
is the 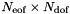 permutation matrix.
permutation matrix.
 and that the resulting local coefficients
and that the resulting local coefficients  will be stored in m_coeffs.
will be stored in m_coeffs. Definition at line 737 of file ContField2D.cpp.
References Nektar::MultiRegions::ExpList::m_coeffs, and m_locToGloMap.
|
privatevirtual |
Solves the two-dimensional Helmholtz equation, subject to the boundary conditions specified.
Consider the two dimensional Helmholtz equation,
![\[\nabla^2u(\boldsymbol{x})-\lambda u(\boldsymbol{x}) = f(\boldsymbol{x}),\]](form_308.png)
supplemented with appropriate boundary conditions (which are contained in the data member m_bndCondExpansions). Applying a 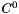 continuous Galerkin discretisation, this equation leads to the following linear system:
continuous Galerkin discretisation, this equation leads to the following linear system:
![\[\left(\boldsymbol{L}+\lambda\boldsymbol{M}\right) \boldsymbol{\hat{u}}_g=\boldsymbol{\hat{f}}\]](form_309.png)
where 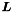 and
and 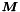 are the Laplacian and mass matrix respectively. This function solves the system above for the global coefficients
are the Laplacian and mass matrix respectively. This function solves the system above for the global coefficients 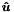 by a call to the function GlobalSolve. It is assumed #m_coeff contains an initial estimate for the solution.
by a call to the function GlobalSolve. It is assumed #m_coeff contains an initial estimate for the solution.
The values of the function  evaluated at the quadrature points
evaluated at the quadrature points 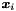 should be contained in the variable m_phys of the ExpList object inarray. The resulting global coefficients
should be contained in the variable m_phys of the ExpList object inarray. The resulting global coefficients  are stored in the array #m_contCoeffs or m_coeffs depending on whether coeffstate is eGlobal or eLocal
are stored in the array #m_contCoeffs or m_coeffs depending on whether coeffstate is eGlobal or eLocal
| inarray | An ExpList, containing the discrete evaluation of the forcing function  at the quadrature points in its array m_phys. at the quadrature points in its array m_phys. |
| lambda | The parameter 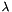 of the Helmholtz equation of the Helmholtz equation |
Definition at line 814 of file ContField2D.cpp.
References Nektar::SpatialDomains::eDirichlet, Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eHelmholtz, Nektar::eUseGlobal, Nektar::MultiRegions::ExpList::GetNcoeffs(), GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), IProductWRTBase(), Nektar::FlagList::isSet(), Nektar::MultiRegions::ExpList::LocalToGlobal(), Nektar::MultiRegions::DisContField2D::m_bndCondExpansions, Nektar::MultiRegions::DisContField2D::m_bndConditions, m_locToGloMap, Vmath::Neg(), and Vmath::Vadd().
|
privatevirtual |
Impose the Dirichlet Boundary Conditions on outarray.
Definition at line 631 of file ContField2D.cpp.
References Nektar::SpatialDomains::eDirichlet, Nektar::MultiRegions::ExpList::GetNcoeffs(), Nektar::iterator, Nektar::MultiRegions::DisContField2D::m_bndCondExpansions, Nektar::MultiRegions::DisContField2D::m_bndConditions, m_locToGloMap, sign, and Vmath::Vcopy().
Referenced by GlobalSolve().
|
privatevirtual |
First compute the inner product of forcing function with respect to base, and then solve the system with the linear advection operator.
| velocity | Array of advection velocities in physical space |
| inarray | Forcing function. |
| outarray | Result. |
| lambda | reaction coefficient |
| coeffstate | State of Coefficients, Local or Global |
| dirForcing | Dirichlet Forcing. |
Definition at line 936 of file ContField2D.cpp.
References Nektar::SpatialDomains::eDirichlet, Nektar::StdRegions::eFactorLambda, Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eLinearAdvectionDiffusionReaction, Nektar::StdRegions::eVarCoeffVelX, Nektar::StdRegions::eVarCoeffVelY, Nektar::MultiRegions::ExpList::GetNcoeffs(), GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), IProductWRTBase(), Nektar::MultiRegions::DisContField2D::m_bndCondExpansions, Nektar::MultiRegions::DisContField2D::m_bndConditions, m_locToGloMap, Vmath::Neg(), and Vmath::Vadd().
|
private |
First compute the inner product of forcing function with respect to base, and then solve the system with the linear advection operator.
| velocity | Array of advection velocities in physical space |
| inarray | Forcing function. |
| outarray | Result. |
| lambda | reaction coefficient |
| coeffstate | State of Coefficients, Local or Global |
| dirForcing | Dirichlet Forcing. |
Definition at line 1005 of file ContField2D.cpp.
References Nektar::StdRegions::eFactorLambda, Nektar::MultiRegions::eGlobal, Nektar::StdRegions::eLinearAdvectionReaction, Nektar::StdRegions::eVarCoeffVelX, Nektar::StdRegions::eVarCoeffVelY, GlobalSolve(), Nektar::MultiRegions::ExpList::GlobalToLocal(), IProductWRTBase(), and m_locToGloMap.
Gathers the global coefficients  from the local coefficients
from the local coefficients  .
.
This operation is evaluated as:
![\begin{tabbing} \hspace{1cm} \= Do \= $e=$ $1, N_{\mathrm{el}}$ \\ \> \> Do \= $i=$ $0,N_m^e-1$ \\ \> \> \> $\boldsymbol{\hat{u}}_g[\mbox{map}[e][i]] = \mbox{sign}[e][i] \cdot \boldsymbol{\hat{u}}^{e}[i]$\\ \> \> continue\\ \> continue \end{tabbing}](form_272.png)
where map ![$[e][i]$](form_273.png) is the mapping array and sign
is the mapping array and sign ![$[e][i]$](form_273.png) is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation
is an array of similar dimensions ensuring the correct modal connectivity between the different elements (both these arrays are contained in the data member m_locToGloMap). This operation is equivalent to the gather operation 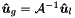 , where
, where  is the
is the  permutation matrix.
permutation matrix.
 and that the resulting global coefficients
and that the resulting global coefficients  will be stored in m_coeffs.
will be stored in m_coeffs. Definition at line 768 of file ContField2D.cpp.
References Nektar::MultiRegions::ExpList::m_coeffs, and m_locToGloMap.
|
privatevirtual |
Template method virtual forwarder for MultiplyByInvMassMatrix().
Definition at line 776 of file ContField2D.cpp.
References MultiplyByInvMassMatrix().
|
privatevirtual |
Template method virtual forwarded for SmoothField().
Definition at line 269 of file ContField2D.cpp.
References BwdTrans(), Nektar::MultiRegions::eGlobal, IProductWRTBase(), m_locToGloMap, and MultiplyByInvMassMatrix().
|
private |
A manager which collects all the global linear systems being assembled, such that they should be constructed only once.
Definition at line 192 of file ContField2D.h.
Referenced by GetGlobalLinSys().
|
private |
(A shared pointer to) a list which collects all the global matrices being assembled, such that they should be constructed only once.
Definition at line 187 of file ContField2D.h.
Referenced by GetGlobalMatrix(), and GetGlobalMatrixNnz().
|
private |
(A shared pointer to) the object which contains all the required information for the transformation from local to global degrees of freedom.
Definition at line 182 of file ContField2D.h.
Referenced by Assemble(), BwdTrans(), ContField2D(), FwdTrans(), GenGlobalLinSys(), GetGlobalMatrix(), GetLocalToGlobalMap(), GlobalSolve(), GlobalToLocal(), IProductWRTBase(), LaplaceSolve(), LinearAdvectionEigs(), LocalToGlobal(), MultiplyByInvMassMatrix(), v_FillBndCondFromField(), v_GeneralMatrixOp(), v_GlobalToLocal(), v_HelmSolve(), v_ImposeDirichletConditions(), v_LinearAdvectionDiffusionReactionSolve(), v_LinearAdvectionReactionSolve(), v_LocalToGlobal(), and v_SmoothField().
 1.8.1.2
1.8.1.2