#include <HexExp.h>

Inheritance diagram for Nektar::LocalRegions::HexExp:

Collaboration diagram for Nektar::LocalRegions::HexExp:

Public Member Functions
	HexExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc, const SpatialDomains::HexGeomSharedPtr &geom)
	Constructor using BasisKey class for quadrature points and order definition. More...

	HexExp (const HexExp &T)
	Copy Constructor. More...

	~HexExp ()
	Destructor. More...

Public Member Functions inherited from Nektar::StdRegions::StdHexExp
	StdHexExp ()

	StdHexExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc)

	StdHexExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc, NekDouble coeffs, NekDouble phys)

	StdHexExp (const StdHexExp &T)

	~StdHexExp ()

Public Member Functions inherited from Nektar::StdRegions::StdExpansion3D
	StdExpansion3D ()

	StdExpansion3D (int numcoeffs, const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb, const LibUtilities::BasisKey &Bc)

	StdExpansion3D (const StdExpansion3D &T)

virtual	~StdExpansion3D ()

void	PhysTensorDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray_d1, Array< OneD, NekDouble > &outarray_d2, Array< OneD, NekDouble > &outarray_d3)
	Calculate the 3D derivative in the local tensor/collapsed coordinate at the physical points. More...

void	BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)

void	IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)

Public Member Functions inherited from Nektar::StdRegions::StdExpansion
	StdExpansion ()
	Default Constructor. More...

	StdExpansion (const int numcoeffs, const int numbases, const LibUtilities::BasisKey &Ba=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bb=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bc=LibUtilities::NullBasisKey)
	Constructor. More...

	StdExpansion (const StdExpansion &T)
	Copy Constructor. More...

virtual	~StdExpansion ()
	Destructor. More...

int	GetNumBases () const
	This function returns the number of 1D bases used in the expansion. More...

const Array< OneD, const LibUtilities::BasisSharedPtr > &	GetBase () const
	This function gets the shared point to basis. More...

const LibUtilities::BasisSharedPtr &	GetBasis (int dir) const
	This function gets the shared point to basis in the dir direction. More...

int	GetNcoeffs (void) const
	This function returns the total number of coefficients used in the expansion. More...

int	GetTotPoints () const
	This function returns the total number of quadrature points used in the element. More...

LibUtilities::BasisType	GetBasisType (const int dir) const
	This function returns the type of basis used in the dir direction. More...

int	GetBasisNumModes (const int dir) const
	This function returns the number of expansion modes in the dir direction. More...

int	EvalBasisNumModesMax (void) const
	This function returns the maximum number of expansion modes over all local directions. More...

LibUtilities::PointsType	GetPointsType (const int dir) const
	This function returns the type of quadrature points used in the dir direction. More...

int	GetNumPoints (const int dir) const
	This function returns the number of quadrature points in the dir direction. More...

const Array< OneD, const NekDouble > &	GetPoints (const int dir) const
	This function returns a pointer to the array containing the quadrature points in dir direction. More...

int	GetNverts () const
	This function returns the number of vertices of the expansion domain. More...

int	GetNedges () const
	This function returns the number of edges of the expansion domain. More...

int	GetEdgeNcoeffs (const int i) const
	This function returns the number of expansion coefficients belonging to the i-th edge. More...

int	GetTotalEdgeIntNcoeffs () const

int	GetEdgeNumPoints (const int i) const
	This function returns the number of quadrature points belonging to the i-th edge. More...

int	DetCartesianDirOfEdge (const int edge)

const LibUtilities::BasisKey	DetEdgeBasisKey (const int i) const

const LibUtilities::BasisKey	DetFaceBasisKey (const int i, const int k) const

int	GetFaceNumPoints (const int i) const
	This function returns the number of quadrature points belonging to the i-th face. More...

int	GetFaceNcoeffs (const int i) const
	This function returns the number of expansion coefficients belonging to the i-th face. More...

int	GetFaceIntNcoeffs (const int i) const

int	GetTotalFaceIntNcoeffs () const

int	GetTraceNcoeffs (const int i) const
	This function returns the number of expansion coefficients belonging to the i-th edge/face. More...

LibUtilities::PointsKey	GetFacePointsKey (const int i, const int j) const

int	NumBndryCoeffs (void) const

int	NumDGBndryCoeffs (void) const

LibUtilities::BasisType	GetEdgeBasisType (const int i) const
	This function returns the type of expansion basis on the i-th edge. More...

const LibUtilities::PointsKey	GetNodalPointsKey () const
	This function returns the type of expansion Nodal point type if defined. More...

int	GetNfaces () const
	This function returns the number of faces of the expansion domain. More...

int	GetNtrace () const
	Returns the number of trace elements connected to this element. More...

LibUtilities::ShapeType	DetShapeType () const
	This function returns the shape of the expansion domain. More...

boost::shared_ptr< StdExpansion >	GetStdExp (void) const

int	GetShapeDimension () const

bool	IsBoundaryInteriorExpansion ()

bool	IsNodalNonTensorialExp ()

void	BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	This function performs the Backward transformation from coefficient space to physical space. More...

void	FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	This function performs the Forward transformation from physical space to coefficient space. More...

void	FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

NekDouble	Integral (const Array< OneD, const NekDouble > &inarray)
	This function integrates the specified function over the domain. More...

void	FillMode (const int mode, Array< OneD, NekDouble > &outarray)
	This function fills the array outarray with the mode-th mode of the expansion. More...

void	IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	this function calculates the inner product of a given function f with the different modes of the expansion More...

void	IProductWRTBase (const Array< OneD, const NekDouble > &base, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, int coll_check)

void	IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

int	GetElmtId ()
	Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...

void	SetElmtId (const int id)
	Set the element id of this expansion when used in a list by returning value of m_elmt_id. More...

void	GetCoords (Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2=NullNekDouble1DArray, Array< OneD, NekDouble > &coords_3=NullNekDouble1DArray)
	this function returns the physical coordinates of the quadrature points of the expansion More...

void	GetCoord (const Array< OneD, const NekDouble > &Lcoord, Array< OneD, NekDouble > &coord)
	given the coordinates of a point of the element in the local collapsed coordinate system, this function calculates the physical coordinates of the point More...

DNekMatSharedPtr	GetStdMatrix (const StdMatrixKey &mkey)

DNekBlkMatSharedPtr	GetStdStaticCondMatrix (const StdMatrixKey &mkey)

IndexMapValuesSharedPtr	GetIndexMap (const IndexMapKey &ikey)

const Array< OneD, const NekDouble > &	GetPhysNormals (void)

void	SetPhysNormals (Array< OneD, const NekDouble > &normal)

virtual void	SetUpPhysNormals (const int edge)

void	NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, Array< OneD, NekDouble > &outarray)

void	NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, NekDouble > &Fy, Array< OneD, NekDouble > &outarray)

void	NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)

void	NormVectorIProductWRTBase (const Array< OneD, const Array< OneD, NekDouble > > &Fvec, Array< OneD, NekDouble > &outarray)

DNekScalBlkMatSharedPtr	GetLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)

void	DropLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)

StdRegions::Orientation	GetForient (int face)

StdRegions::Orientation	GetEorient (int edge)

StdRegions::Orientation	GetPorient (int point)

StdRegions::Orientation	GetCartesianEorient (int edge)

void	SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)

void	SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

int	CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)

void	ExtractDataToCoeffs (const NekDouble data, const std::vector< unsigned int > &nummodes, const int nmodes_offset, NekDouble coeffs)

NekDouble	StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)

int	GetCoordim ()

void	GetBoundaryMap (Array< OneD, unsigned int > &outarray)

void	GetInteriorMap (Array< OneD, unsigned int > &outarray)

int	GetVertexMap (const int localVertexId, bool useCoeffPacking=false)

void	GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)

void	GetFaceInteriorMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)

void	GetEdgeToElementMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int P=-1)

void	GetFaceToElementMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int nummodesA=-1, int nummodesB=-1)

void	GetEdgePhysVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Extract the physical values along edge edge from inarray into outarray following the local edge orientation and point distribution defined by defined in EdgeExp. More...

void	GetEdgePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GetTracePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GetVertexPhysVals (const int vertex, const Array< OneD, const NekDouble > &inarray, NekDouble &outarray)

void	GetEdgeInterpVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GetEdgeQFactors (const int edge, Array< OneD, NekDouble > &outarray)
	Extract the metric factors to compute the contravariant fluxes along edge edge and stores them into outarray following the local edge orientation (i.e. anticlockwise convention). More...

void	GetFacePhysVals (const int face, const boost::shared_ptr< StdExpansion > &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient=eNoOrientation)

void	GetEdgePhysMap (const int edge, Array< OneD, int > &outarray)

void	GetFacePhysMap (const int face, Array< OneD, int > &outarray)

void	MultiplyByQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

DNekMatSharedPtr	CreateGeneralMatrix (const StdMatrixKey &mkey)
	this function generates the mass matrix $\mathbf{M}[i][j] = \int \phi_i(\mathbf{x}) \phi_j(\mathbf{x}) d\mathbf{x}$ More...

void	GeneralMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdMatrixKey &mkey)

void	LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDerivMatrixOp (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDirectionalDerivMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassLevelCurvatureMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LinearAdvectionDiffusionReactionMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)

void	HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

DNekMatSharedPtr	GenMatrix (const StdMatrixKey &mkey)

void	PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)

void	PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	PhysDeriv_s (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_ds)

void	PhysDeriv_n (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_dn)

void	PhysDirectionalDeriv (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &direction, Array< OneD, NekDouble > &outarray)

void	StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)

void	StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	AddRobinMassMatrix (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, DNekMatSharedPtr &inoutmat)

void	AddRobinEdgeContribution (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, Array< OneD, NekDouble > &coeffs)

NekDouble	PhysEvaluate (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
	This function evaluates the expansion at a single (arbitrary) point of the domain. More...

NekDouble	PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)
	This function evaluates the expansion at a single (arbitrary) point of the domain. More...

void	LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)
	Convert local cartesian coordinate xi into local collapsed coordinates eta. More...

const boost::shared_ptr < SpatialDomains::GeomFactors > &	GetMetricInfo (void) const

virtual int	v_GetElmtId ()
	Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...

virtual const Array< OneD, const NekDouble > &	v_GetPhysNormals (void)

virtual void	v_SetPhysNormals (Array< OneD, const NekDouble > &normal)

virtual void	v_SetUpPhysNormals (const int edge)

virtual void	v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, Array< OneD, NekDouble > &outarray)

virtual void	v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)

virtual void	v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)

virtual StdRegions::Orientation	v_GetEorient (int edge)

virtual StdRegions::Orientation	v_GetCartesianEorient (int edge)

virtual StdRegions::Orientation	v_GetPorient (int point)

NekDouble	Linf (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
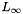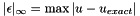	Function to evaluate the discrete $L_\infty$ error $\|\epsilon\|_\infty = \max \|u - u_{exact}\|$ where $u_{exact}$ is given by the array sol. More...

NekDouble	L2 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
	Function to evaluate the discrete 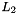error, $\| \epsilon \|_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 dx \right]^{1/2} d\xi_1$ where $u_{exact}$ is given by the array sol. More...

NekDouble	H1 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
	Function to evaluate the discrete 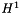error, $\| \epsilon \|^1_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 + \nabla(u - u_{exact})\cdot\nabla(u - u_{exact})\cdot dx \right]^{1/2} d\xi_1$ where $u_{exact}$ is given by the array sol. More...

const NormalVector &	GetEdgeNormal (const int edge) const

void	ComputeEdgeNormal (const int edge)

void	NegateEdgeNormal (const int edge)

bool	EdgeNormalNegated (const int edge)

void	ComputeFaceNormal (const int face)

void	NegateFaceNormal (const int face)

bool	FaceNormalNegated (const int face)

void	ComputeVertexNormal (const int vertex)

const NormalVector &	GetFaceNormal (const int face) const

const NormalVector &	GetVertexNormal (const int vertex) const

const NormalVector &	GetSurfaceNormal (const int id) const

const LibUtilities::PointsKeyVector	GetPointsKeys () const

Array< OneD, unsigned int >	GetEdgeInverseBoundaryMap (int eid)

Array< OneD, unsigned int >	GetFaceInverseBoundaryMap (int fid, StdRegions::Orientation faceOrient=eNoOrientation)

DNekMatSharedPtr	BuildInverseTransformationMatrix (const DNekScalMatSharedPtr &m_transformationmatrix)

void	PhysInterpToSimplexEquiSpaced (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, int npset=-1)
	This function performs an interpolation from the physical space points provided at input into an array of equispaced points which are not the collapsed coordinate. So for a tetrahedron you will only get a tetrahedral number of values. More...

void	GetSimplexEquiSpacedConnectivity (Array< OneD, int > &conn, bool standard=true)
	This function provides the connectivity of local simplices (triangles or tets) to connect the equispaced data points provided by PhysInterpToSimplexEquiSpaced. More...

void	EquiSpacedToCoeffs (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	This function performs a projection/interpolation from the equispaced points sometimes used in post-processing onto the coefficient space. More...

template<class T >
boost::shared_ptr< T >	as ()

void	IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)

Public Member Functions inherited from Nektar::LocalRegions::Expansion3D
	Expansion3D (SpatialDomains::Geometry3DSharedPtr pGeom)

virtual	~Expansion3D ()

void	SetFaceExp (const int face, Expansion2DSharedPtr &f)

Expansion2DSharedPtr	GetFaceExp (const int face)

void	SetTraceToGeomOrientation (Array< OneD, NekDouble > &inout)
	Align trace orientation with the geometry orientation. More...

void	SetFaceToGeomOrientation (const int face, Array< OneD, NekDouble > &inout)
	Align face orientation with the geometry orientation. More...

void	AddHDGHelmholtzFaceTerms (const NekDouble tau, const int edge, Array< OneD, NekDouble > &facePhys, const StdRegions::VarCoeffMap &dirForcing, Array< OneD, NekDouble > &outarray)

void	AddNormTraceInt (const int dir, Array< OneD, ExpansionSharedPtr > &FaceExp, Array< OneD, Array< OneD, NekDouble > > &faceCoeffs, Array< OneD, NekDouble > &outarray)

void	AddNormTraceInt (const int dir, Array< OneD, const NekDouble > &inarray, Array< OneD, ExpansionSharedPtr > &FaceExp, Array< OneD, NekDouble > &outarray, const StdRegions::VarCoeffMap &varcoeffs)

void	AddFaceBoundaryInt (const int face, ExpansionSharedPtr &FaceExp, Array< OneD, NekDouble > &facePhys, Array< OneD, NekDouble > &outarray, const StdRegions::VarCoeffMap &varcoeffs=StdRegions::NullVarCoeffMap)

SpatialDomains::Geometry3DSharedPtr	GetGeom3D () const

void	ReOrientFacePhysMap (const int nvert, const StdRegions::Orientation orient, const int nq0, const int nq1, Array< OneD, int > &idmap)

void	v_NormVectorIProductWRTBase (const Array< OneD, const Array< OneD, NekDouble > > &Fvec, Array< OneD, NekDouble > &outarray)

Public Member Functions inherited from Nektar::LocalRegions::Expansion
	Expansion (SpatialDomains::GeometrySharedPtr pGeom)

	Expansion (const Expansion &pSrc)

virtual	~Expansion ()

DNekScalMatSharedPtr	GetLocMatrix (const LocalRegions::MatrixKey &mkey)

DNekScalMatSharedPtr	GetLocMatrix (const StdRegions::MatrixType mtype, const StdRegions::ConstFactorMap &factors=StdRegions::NullConstFactorMap, const StdRegions::VarCoeffMap &varcoeffs=StdRegions::NullVarCoeffMap)

SpatialDomains::GeometrySharedPtr	GetGeom () const

void	Reset ()

virtual const SpatialDomains::GeomFactorsSharedPtr &	v_GetMetricInfo () const

DNekMatSharedPtr	BuildTransformationMatrix (const DNekScalMatSharedPtr &r_bnd, const StdRegions::MatrixType matrixType)

DNekMatSharedPtr	BuildVertexMatrix (const DNekScalMatSharedPtr &r_bnd)

void	AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)

void	AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)

void	AddFaceNormBoundaryInt (const int face, const boost::shared_ptr< Expansion > &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)

void	DGDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, ExpansionSharedPtr > &EdgeExp, Array< OneD, Array< OneD, NekDouble > > &coeffs, Array< OneD, NekDouble > &outarray)

Protected Member Functions
virtual NekDouble	v_Integral (const Array< OneD, const NekDouble > &inarray)
	Integrate the physical point list inarray over region. More...

virtual void	v_PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2)
	Calculate the derivative of the physical points. More...

virtual void	v_PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Calculate the derivative of the physical points in a single direction. More...

virtual void	v_FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Forward transform from physical quadrature space stored in inarray and evaluate the expansion coefficients and store in (this)->_coeffs. More...

virtual void	v_IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Calculate the inner product of inarray with respect to the elements basis. More...

virtual void	v_IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)
	Calculate the inner product of inarray with respect to the given basis B = base0 * base1 * base2. More...

virtual void	v_IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Calculates the inner product 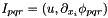$I_{pqr} = (u, \partial_{x_i} \phi_{pqr})$ . More...

void	IProductWRTDerivBase_MatOp (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual NekDouble	v_StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)

virtual NekDouble	v_PhysEvaluate (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
	This function evaluates the expansion at a single (arbitrary) point of the domain. More...

virtual void	v_GetCoord (const Array< OneD, const NekDouble > &Lcoords, Array< OneD, NekDouble > &coords)
	Retrieves the physical coordinates of a given set of reference coordinates. More...

virtual void	v_GetCoords (Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2, Array< OneD, NekDouble > &coords_3)

virtual LibUtilities::ShapeType	v_DetShapeType () const
	Return the region shape using the enum-list of ShapeType. More...

virtual StdRegions::StdExpansionSharedPtr	v_GetStdExp (void) const

virtual void	v_ExtractDataToCoeffs (const NekDouble data, const std::vector< unsigned int > &nummodes, const int mode_offset, NekDouble coeffs)
	Unpack data from input file assuming it comes from the same expansion type. More...

virtual bool	v_GetFaceDGForwards (const int i) const

virtual void	v_GetFacePhysMap (const int face, Array< OneD, int > &outarray)

void	v_ComputeFaceNormal (const int face)

virtual void	v_MassMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_WeakDerivMatrixOp (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_WeakDirectionalDerivMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_MassLevelCurvatureMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

void	v_GeneralMatrixOp_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdRegions::StdMatrixKey &mkey)

virtual DNekMatSharedPtr	v_GenMatrix (const StdRegions::StdMatrixKey &mkey)

virtual DNekMatSharedPtr	v_CreateStdMatrix (const StdRegions::StdMatrixKey &mkey)

DNekScalMatSharedPtr	CreateMatrix (const MatrixKey &mkey)

DNekScalBlkMatSharedPtr	CreateStaticCondMatrix (const MatrixKey &mkey)

virtual DNekScalMatSharedPtr	v_GetLocMatrix (const MatrixKey &mkey)

virtual DNekScalBlkMatSharedPtr	v_GetLocStaticCondMatrix (const MatrixKey &mkey)

void	v_DropLocStaticCondMatrix (const MatrixKey &mkey)

virtual void	v_ComputeLaplacianMetric ()

Protected Member Functions inherited from Nektar::StdRegions::StdHexExp
virtual void	v_StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2)

virtual void	v_StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)

virtual void	v_IProductWRTBase_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &base2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1, bool doCheckCollDir2)

virtual void	v_IProductWRTDerivBase_MatOp (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)

virtual void	v_FillMode (const int mode, Array< OneD, NekDouble > &outarray)

virtual int	v_GetNverts () const

virtual int	v_GetNedges () const

virtual int	v_GetNfaces () const

virtual int	v_NumBndryCoeffs () const

virtual int	v_NumDGBndryCoeffs () const

virtual int	v_GetEdgeNcoeffs (const int i) const

virtual int	v_GetTotalEdgeIntNcoeffs () const

virtual int	v_GetFaceNcoeffs (const int i) const

virtual int	v_GetFaceIntNcoeffs (const int i) const

virtual int	v_GetTotalFaceIntNcoeffs () const

virtual int	v_GetFaceNumPoints (const int i) const

virtual LibUtilities::PointsKey	v_GetFacePointsKey (const int i, const int j) const

virtual int	v_CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)

virtual const LibUtilities::BasisKey	v_DetFaceBasisKey (const int i, const int k) const

virtual LibUtilities::BasisType	v_GetEdgeBasisType (const int i) const

virtual bool	v_IsBoundaryInteriorExpansion ()

virtual void	v_GetFaceToElementMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int nummodesA=-1, int nummodesB=-1)

virtual int	v_GetVertexMap (int localVertexId, bool useCoeffPacking=false)

virtual void	v_GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)

virtual void	v_GetFaceInteriorMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)

virtual void	v_GetInteriorMap (Array< OneD, unsigned int > &outarray)

virtual void	v_GetBoundaryMap (Array< OneD, unsigned int > &outarray)

virtual void	v_MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

Protected Member Functions inherited from Nektar::StdRegions::StdExpansion3D
virtual NekDouble	v_PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)

virtual void	v_LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_NegateFaceNormal (const int face)

virtual bool	v_FaceNormalNegated (const int face)

virtual int	v_GetTraceNcoeffs (const int i) const

Protected Member Functions inherited from Nektar::StdRegions::StdExpansion
DNekMatSharedPtr	CreateStdMatrix (const StdMatrixKey &mkey)

DNekBlkMatSharedPtr	CreateStdStaticCondMatrix (const StdMatrixKey &mkey)
	Create the static condensation of a matrix when using a boundary interior decomposition. More...

IndexMapValuesSharedPtr	CreateIndexMap (const IndexMapKey &ikey)
	Create an IndexMap which contains mapping information linking any specific element shape with either its boundaries, edges, faces, verteces, etc. More...

void	BwdTrans_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GeneralMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp_MatFree_Kernel (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp)

void	LaplacianMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp_MatFree (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDerivMatrixOp_MatFree (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDirectionalDerivMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassLevelCurvatureMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LinearAdvectionDiffusionReactionMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)

void	HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	HelmholtzMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)

Protected Member Functions inherited from Nektar::LocalRegions::Expansion3D
virtual void	v_DGDeriv (const int dir, const Array< OneD, const NekDouble > &incoeffs, Array< OneD, ExpansionSharedPtr > &FaceExp, Array< OneD, Array< OneD, NekDouble > > &faceCoeffs, Array< OneD, NekDouble > &out_d)
	Evaluate coefficients of weak deriviative in the direction dir given the input coefficicents incoeffs and the imposed boundary values in EdgeExp (which will have its phys space updated). More...

virtual void	v_AddFaceNormBoundaryInt (const int face, const ExpansionSharedPtr &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)

virtual void	v_AddRobinMassMatrix (const int face, const Array< OneD, const NekDouble > &primCoeffs, DNekMatSharedPtr &inoutmat)

virtual StdRegions::Orientation	v_GetForient (int face)

virtual void	v_GetTracePhysVals (const int face, const StdRegions::StdExpansionSharedPtr &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient)
	Returns the physical values at the quadrature points of a face Wrapper function to v_GetFacePhysVals. More...

virtual void	v_GetFacePhysVals (const int face, const StdRegions::StdExpansionSharedPtr &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient)

virtual Array< OneD, unsigned int >	v_GetEdgeInverseBoundaryMap (int eid)

virtual Array< OneD, unsigned int >	v_GetFaceInverseBoundaryMap (int fid, StdRegions::Orientation faceOrient=StdRegions::eNoOrientation)

virtual DNekMatSharedPtr	v_BuildTransformationMatrix (const DNekScalMatSharedPtr &r_bnd, const StdRegions::MatrixType matrixType)

virtual DNekMatSharedPtr	v_BuildInverseTransformationMatrix (const DNekScalMatSharedPtr &m_transformationmatrix)
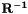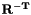	Build inverse and inverse transposed transformation matrix: $\mathbf{R^{-1}}$ and $\mathbf{R^{-T}}$ . More...

virtual DNekMatSharedPtr	v_BuildVertexMatrix (const DNekScalMatSharedPtr &r_bnd)

void	ReOrientTriFacePhysMap (const StdRegions::Orientation orient, const int nq0, const int nq1, Array< OneD, int > &idmap)

void	ReOrientQuadFacePhysMap (const StdRegions::Orientation orient, const int nq0, const int nq1, Array< OneD, int > &idmap)

Protected Member Functions inherited from Nektar::LocalRegions::Expansion
void	ComputeLaplacianMetric ()

void	ComputeQuadratureMetric ()

virtual void	v_MultiplyByQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)

virtual void	v_AddEdgeNormBoundaryInt (const int edge, const boost::shared_ptr< Expansion > &EdgeExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)

virtual void	v_AddFaceNormBoundaryInt (const int face, const boost::shared_ptr< Expansion > &FaceExp, const Array< OneD, const NekDouble > &Fn, Array< OneD, NekDouble > &outarray)

Private Member Functions
	HexExp ()

virtual void	v_LaplacianMatrixOp_MatFree_Kernel (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp)

Private Attributes
LibUtilities::NekManager < MatrixKey, DNekScalMat, MatrixKey::opLess >	m_matrixManager

LibUtilities::NekManager < MatrixKey, DNekScalBlkMat, MatrixKey::opLess >	m_staticCondMatrixManager

Additional Inherited Members
Protected Attributes inherited from Nektar::StdRegions::StdExpansion3D
std::map< int, NormalVector >	m_faceNormals

std::map< int, bool >	m_negatedNormals

Protected Attributes inherited from Nektar::StdRegions::StdExpansion
Array< OneD, LibUtilities::BasisSharedPtr >	m_base

int	m_elmt_id

int	m_ncoeffs

LibUtilities::NekManager < StdMatrixKey, DNekMat, StdMatrixKey::opLess >	m_stdMatrixManager

LibUtilities::NekManager < StdMatrixKey, DNekBlkMat, StdMatrixKey::opLess >	m_stdStaticCondMatrixManager

LibUtilities::NekManager < IndexMapKey, IndexMapValues, IndexMapKey::opLess >	m_IndexMapManager

Protected Attributes inherited from Nektar::LocalRegions::Expansion
SpatialDomains::GeometrySharedPtr	m_geom

SpatialDomains::GeomFactorsSharedPtr	m_metricinfo

MetricMap	m_metrics

Detailed Description

Defines a hexahedral local expansion.

Definition at line 64 of file HexExp.h.

Constructor & Destructor Documentation

Nektar::LocalRegions::HexExp::HexExp	(	const LibUtilities::BasisKey &	Ba,
		const LibUtilities::BasisKey &	Bb,
		const LibUtilities::BasisKey &	Bc,
		const SpatialDomains::HexGeomSharedPtr &	geom
	)

Constructor using BasisKey class for quadrature points and order definition.

Parameters

Ba	Basis key for first coordinate.
Bb	Basis key for second coordinate.
Bc	Basis key for third coordinate.

Definition at line 59 of file HexExp.cpp.

                                                                   :
             StdExpansion  (Ba.GetNumModes()*Bb.GetNumModes()*Bc.GetNumModes(),3,Ba,Bb,Bc),
             StdExpansion3D(Ba.GetNumModes()*Bb.GetNumModes()*Bc.GetNumModes(),Ba,Bb,Bc),
             StdRegions::StdHexExp(Ba,Bb,Bc),
             Expansion     (geom),
             Expansion3D   (geom),
             m_matrixManager(
                     boost::bind(&HexExp::CreateMatrix, this, _1),
                     std::string("HexExpMatrix")),
             m_staticCondMatrixManager(
                     boost::bind(&HexExp::CreateStaticCondMatrix, this, _1),
                     std::string("HexExpStaticCondMatrix"))
         {
         }

Nektar::LocalRegions::HexExp::HexExp ( const HexExp & T )

Copy Constructor.

Parameters

T	HexExp to copy.

Definition at line 83 of file HexExp.cpp.

                                      :
             StdRegions::StdHexExp(T),
             Expansion(T),
             Expansion3D(T),
             m_matrixManager(T.m_matrixManager),
             m_staticCondMatrixManager(T.m_staticCondMatrixManager)
         {
         }

Nektar::LocalRegions::HexExp::~HexExp ( )

Destructor.

Definition at line 95 of file HexExp.cpp.

96 {

97 }

Nektar::LocalRegions::HexExp::HexExp ( )

private

Member Function Documentation

DNekScalMatSharedPtr Nektar::LocalRegions::HexExp::CreateMatrix ( const MatrixKey & mkey )

protected

Definition at line 1308 of file HexExp.cpp.

         {
             DNekScalMatSharedPtr returnval;
             LibUtilities::PointsKeyVector ptsKeys = GetPointsKeys();
 
             ASSERTL2(m_metricinfo->GetGtype() != SpatialDomains::eNoGeomType,
                      "Geometric information is not set up");
 
             switch(mkey.GetMatrixType())
             {
             case StdRegions::eMass:
                 {
                     if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
                             mkey.GetNVarCoeff())
                     {
                         NekDouble one = 1.0;
                         DNekMatSharedPtr mat = GenMatrix(mkey);
                         returnval = MemoryManager<DNekScalMat>
                                                 ::AllocateSharedPtr(one,mat);
                     }
                     else
                     {
                         NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
                         DNekMatSharedPtr mat
                                         = GetStdMatrix(mkey);
                         returnval = MemoryManager<DNekScalMat>
                                                 ::AllocateSharedPtr(jac,mat);
                     }
                 }
                 break;
             case StdRegions::eInvMass:
                 {
                     if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
                     {
                         NekDouble one = 1.0;
                         StdRegions::StdMatrixKey masskey(StdRegions::eMass,
                                                     DetShapeType(), *this);
                         DNekMatSharedPtr mat = GenMatrix(masskey);
                         mat->Invert();
 
                         returnval = MemoryManager<DNekScalMat>
                                                 ::AllocateSharedPtr(one,mat);
                     }
                     else
                     {
                         NekDouble fac = 1.0/(m_metricinfo->GetJac(ptsKeys))[0];
                         DNekMatSharedPtr mat
                                         = GetStdMatrix(mkey);
                         returnval = MemoryManager<DNekScalMat>
                                                 ::AllocateSharedPtr(fac,mat);
                     }
                 }
                 break;
             case StdRegions::eWeakDeriv0:
             case StdRegions::eWeakDeriv1:
             case StdRegions::eWeakDeriv2:
                 {
                     if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
                             mkey.GetNVarCoeff())
                     {
                         NekDouble one = 1.0;
                         DNekMatSharedPtr mat = GenMatrix(mkey);
 
                         returnval = MemoryManager<DNekScalMat>
                                                 ::AllocateSharedPtr(one,mat);
                     }
                     else
                     {
                         NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
                         Array<TwoD, const NekDouble> df
                                     = m_metricinfo->GetDerivFactors(ptsKeys);
                         int dir = 0;
 
                         switch(mkey.GetMatrixType())
                         {
                             case StdRegions::eWeakDeriv0:
                                 dir = 0;
                                 break;
                             case StdRegions::eWeakDeriv1:
                                 dir = 1;
                                 break;
                             case StdRegions::eWeakDeriv2:
                                 dir = 2;
                                 break;
                             default:
                                 break;
                         }
 
                         MatrixKey deriv0key(StdRegions::eWeakDeriv0,
                                             mkey.GetShapeType(), *this);
                         MatrixKey deriv1key(StdRegions::eWeakDeriv1,
                                             mkey.GetShapeType(), *this);
                         MatrixKey deriv2key(StdRegions::eWeakDeriv2,
                                             mkey.GetShapeType(), *this);
 
                         DNekMat &deriv0 = *GetStdMatrix(deriv0key);
                         DNekMat &deriv1 = *GetStdMatrix(deriv1key);
                         DNekMat &deriv2 = *GetStdMatrix(deriv2key);
 
                         int rows = deriv0.GetRows();
                         int cols = deriv1.GetColumns();
 
                         DNekMatSharedPtr WeakDeriv = MemoryManager<DNekMat>
                                                 ::AllocateSharedPtr(rows,cols);
 
                         (*WeakDeriv) = df[3*dir  ][0]*deriv0
                                      + df[3*dir+1][0]*deriv1
                                      + df[3*dir+2][0]*deriv2;
 
                         returnval = MemoryManager<DNekScalMat>
                                             ::AllocateSharedPtr(jac,WeakDeriv);
                     }
                 }
                 break;
             case StdRegions::eLaplacian:
                 {
                     if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
                         mkey.GetNVarCoeff()||
                         mkey.ConstFactorExists(
                                 StdRegions::eFactorSVVCutoffRatio))
                     {
                         NekDouble one = 1.0;
                         DNekMatSharedPtr mat = GenMatrix(mkey);
 
                         returnval = MemoryManager<DNekScalMat>
                                                 ::AllocateSharedPtr(one,mat);
                     }
                     else
                     {
                         MatrixKey lap00key(StdRegions::eLaplacian00,
                                            mkey.GetShapeType(), *this);
                         MatrixKey lap01key(StdRegions::eLaplacian01,
                                            mkey.GetShapeType(), *this);
                         MatrixKey lap02key(StdRegions::eLaplacian02,
                                            mkey.GetShapeType(), *this);
                         MatrixKey lap11key(StdRegions::eLaplacian11,
                                            mkey.GetShapeType(), *this);
                         MatrixKey lap12key(StdRegions::eLaplacian12,
                                            mkey.GetShapeType(), *this);
                         MatrixKey lap22key(StdRegions::eLaplacian22,
                                            mkey.GetShapeType(), *this);
 
                         DNekMat &lap00 = *GetStdMatrix(lap00key);
                         DNekMat &lap01 = *GetStdMatrix(lap01key);
                         DNekMat &lap02 = *GetStdMatrix(lap02key);
                         DNekMat &lap11 = *GetStdMatrix(lap11key);
                         DNekMat &lap12 = *GetStdMatrix(lap12key);
                         DNekMat &lap22 = *GetStdMatrix(lap22key);
 
                         NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
                         Array<TwoD, const NekDouble> gmat
                                             = m_metricinfo->GetGmat(ptsKeys);
 
                         int rows = lap00.GetRows();
                         int cols = lap00.GetColumns();
 
                         DNekMatSharedPtr lap = MemoryManager<DNekMat>
                                                 ::AllocateSharedPtr(rows,cols);
 
                         (*lap)  = gmat[0][0]*lap00
                                 + gmat[4][0]*lap11
                                 + gmat[8][0]*lap22
                                 + gmat[3][0]*(lap01 + Transpose(lap01))
                                 + gmat[6][0]*(lap02 + Transpose(lap02))
                                 + gmat[7][0]*(lap12 + Transpose(lap12));
 
                         returnval = MemoryManager<DNekScalMat>
                                                 ::AllocateSharedPtr(jac,lap);
                     }
                 }
                 break;
             case StdRegions::eHelmholtz:
                 {
                     NekDouble lambda = mkey.GetConstFactor(StdRegions::eFactorLambda);
                     MatrixKey masskey(StdRegions::eMass,
                                       mkey.GetShapeType(), *this);
                     DNekScalMat &MassMat = *(this->m_matrixManager[masskey]);
                     MatrixKey lapkey(StdRegions::eLaplacian,
                                      mkey.GetShapeType(), *this, mkey.GetConstFactors(), mkey.GetVarCoeffs());
                     DNekScalMat &LapMat = *(this->m_matrixManager[lapkey]);
 
                     int rows = LapMat.GetRows();
                     int cols = LapMat.GetColumns();
 
                     DNekMatSharedPtr helm = MemoryManager<DNekMat>::AllocateSharedPtr(rows,cols);
 
                     NekDouble one = 1.0;
                     (*helm) = LapMat + lambda*MassMat;
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,helm);
                 }
                 break;
             case StdRegions::eIProductWRTBase:
                 {
                     if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
                     {
                         NekDouble one = 1.0;
                         DNekMatSharedPtr mat = GenMatrix(mkey);
                         returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
                     }
                     else
                     {
                         NekDouble jac = (m_metricinfo->GetJac(ptsKeys))[0];
                         DNekMatSharedPtr mat = GetStdMatrix(mkey);
                         returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(jac,mat);
                     }
                 }
                 break;
             case StdRegions::eHybridDGHelmholtz:
             case StdRegions::eHybridDGLamToU:
             case StdRegions::eHybridDGLamToQ0:
             case StdRegions::eHybridDGLamToQ1:
             case StdRegions::eHybridDGLamToQ2:
             case StdRegions::eHybridDGHelmBndLam:
             case StdRegions::eInvLaplacianWithUnityMean:
                 {
                     NekDouble one    = 1.0;
 
                     DNekMatSharedPtr mat = GenMatrix(mkey);
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
                 }
                 break;
             case StdRegions::eInvHybridDGHelmholtz:
                 {
                     NekDouble one = 1.0;
 
 //                    StdRegions::StdMatrixKey hkey(StdRegions::eHybridDGHelmholtz,
 //                                                  DetShapeType(),*this,
 //                                                  mkey.GetConstant(0),
 //                                                  mkey.GetConstant(1));
                     MatrixKey hkey(StdRegions::eHybridDGHelmholtz, DetShapeType(), *this, mkey.GetConstFactors(), mkey.GetVarCoeffs());
                     DNekMatSharedPtr mat = GenMatrix(hkey);
 
                     mat->Invert();
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
                 }
                 break;
             case StdRegions::ePreconLinearSpace:
                 {
                     NekDouble one = 1.0;
                     MatrixKey helmkey(StdRegions::eHelmholtz, mkey.GetShapeType(), *this, mkey.GetConstFactors(), mkey.GetVarCoeffs());
                     DNekScalBlkMatSharedPtr helmStatCond = GetLocStaticCondMatrix(helmkey);
                     DNekScalMatSharedPtr A =helmStatCond->GetBlock(0,0);
                     DNekMatSharedPtr R=BuildVertexMatrix(A);
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
                 }
                 break;
             case StdRegions::ePreconLinearSpaceMass:
                 {
                     NekDouble one = 1.0;
                     MatrixKey masskey(StdRegions::eMass, mkey.GetShapeType(), *this);
                     DNekScalBlkMatSharedPtr massStatCond = GetLocStaticCondMatrix(masskey);
                     DNekScalMatSharedPtr A =massStatCond->GetBlock(0,0);
                     DNekMatSharedPtr R=BuildVertexMatrix(A);
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
                 }
                 break;
             case StdRegions::ePreconR:
                 {
                     NekDouble one = 1.0;
                     MatrixKey helmkey(StdRegions::eHelmholtz, mkey.GetShapeType(), *this,mkey.GetConstFactors(), mkey.GetVarCoeffs());
                     DNekScalBlkMatSharedPtr helmStatCond = GetLocStaticCondMatrix(helmkey);
                     DNekScalMatSharedPtr A =helmStatCond->GetBlock(0,0);
 
                     DNekScalMatSharedPtr Atmp;
                     DNekMatSharedPtr R=BuildTransformationMatrix(A,mkey.GetMatrixType());
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
                 }
                 break;
             case StdRegions::ePreconRT:
                 {
                     NekDouble one = 1.0;
                     MatrixKey helmkey(StdRegions::eHelmholtz, mkey.GetShapeType(), *this,mkey.GetConstFactors(), mkey.GetVarCoeffs());
                     DNekScalBlkMatSharedPtr helmStatCond = GetLocStaticCondMatrix(helmkey);
                     DNekScalMatSharedPtr A =helmStatCond->GetBlock(0,0);
 
                     DNekScalMatSharedPtr Atmp;
                     DNekMatSharedPtr RT=BuildTransformationMatrix(A,mkey.GetMatrixType());
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,RT);
                 }
                 break;
             case StdRegions::ePreconRMass:
                 {
                     NekDouble one = 1.0;
                     MatrixKey masskey(StdRegions::eMass, mkey.GetShapeType(), *this);
                     DNekScalBlkMatSharedPtr massStatCond = GetLocStaticCondMatrix(masskey);
                     DNekScalMatSharedPtr A =massStatCond->GetBlock(0,0);
 
                     DNekScalMatSharedPtr Atmp;
                     DNekMatSharedPtr R=BuildTransformationMatrix(A,mkey.GetMatrixType());
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,R);
                 }
                 break;
             case StdRegions::ePreconRTMass:
                 {
                     NekDouble one = 1.0;
                     MatrixKey masskey(StdRegions::eMass, mkey.GetShapeType(), *this);
                     DNekScalBlkMatSharedPtr massStatCond = GetLocStaticCondMatrix(masskey);
                     DNekScalMatSharedPtr A =massStatCond->GetBlock(0,0);
 
                     DNekScalMatSharedPtr Atmp;
                     DNekMatSharedPtr RT=BuildTransformationMatrix(A,mkey.GetMatrixType());
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,RT);
                 }
                 break;
             default:
                 {
                     NekDouble        one = 1.0;
                     DNekMatSharedPtr mat = GenMatrix(mkey);
 
                     returnval = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,mat);
                 }
                 break;
             }
 
             return returnval;
         }

DNekScalBlkMatSharedPtr Nektar::LocalRegions::HexExp::CreateStaticCondMatrix ( const MatrixKey & mkey )

protected

Definition at line 1633 of file HexExp.cpp.

         {
             DNekScalBlkMatSharedPtr returnval;
 
             ASSERTL2(m_metricinfo->GetGtype() != SpatialDomains::eNoGeomType,"Geometric information is not set up");
 
             // set up block matrix system
             unsigned int nbdry = NumBndryCoeffs();
             unsigned int nint = (unsigned int)(m_ncoeffs - nbdry);
             unsigned int exp_size[] = {nbdry,nint};
             unsigned int nblks = 2;
             returnval = MemoryManager<DNekScalBlkMat>::AllocateSharedPtr(nblks,nblks,exp_size,exp_size); //Really need a constructor which takes Arrays
             NekDouble factor = 1.0;
 
             switch(mkey.GetMatrixType())
             {
             case StdRegions::eLaplacian:
             case StdRegions::eHelmholtz: // special case since Helmholtz not defined in StdRegions
 
                 // use Deformed case for both regular and deformed geometries
                 factor = 1.0;
                 goto UseLocRegionsMatrix;
                 break;
             default:
                 if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed ||
                         mkey.GetNVarCoeff())
                 {
                     factor = 1.0;
                     goto UseLocRegionsMatrix;
                 }
                 else
                 {
                     DNekScalMatSharedPtr mat = GetLocMatrix(mkey);
                     factor = mat->Scale();
                     goto UseStdRegionsMatrix;
                 }
                 break;
             UseStdRegionsMatrix:
                 {
                     NekDouble            invfactor = 1.0/factor;
                     NekDouble            one = 1.0;
                     DNekBlkMatSharedPtr  mat = GetStdStaticCondMatrix(mkey);
                     DNekScalMatSharedPtr Atmp;
                     DNekMatSharedPtr     Asubmat;
 
                     returnval->SetBlock(0,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,Asubmat = mat->GetBlock(0,0)));
                     returnval->SetBlock(0,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,Asubmat = mat->GetBlock(0,1)));
                     returnval->SetBlock(1,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,Asubmat = mat->GetBlock(1,0)));
                     returnval->SetBlock(1,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(invfactor,Asubmat = mat->GetBlock(1,1)));
                 }
                 break;
             UseLocRegionsMatrix:
                 {
                     int i,j;
                     NekDouble            invfactor = 1.0/factor;
                     NekDouble            one = 1.0;
                     DNekScalMat &mat = *GetLocMatrix(mkey);
                     DNekMatSharedPtr A = MemoryManager<DNekMat>::AllocateSharedPtr(nbdry,nbdry);
                     DNekMatSharedPtr B = MemoryManager<DNekMat>::AllocateSharedPtr(nbdry,nint);
                     DNekMatSharedPtr C = MemoryManager<DNekMat>::AllocateSharedPtr(nint,nbdry);
                     DNekMatSharedPtr D = MemoryManager<DNekMat>::AllocateSharedPtr(nint,nint);
 
                     Array<OneD,unsigned int> bmap(nbdry);
                     Array<OneD,unsigned int> imap(nint);
                     GetBoundaryMap(bmap);
                     GetInteriorMap(imap);
 
                     for(i = 0; i < nbdry; ++i)
                     {
                         for(j = 0; j < nbdry; ++j)
                         {
                             (*A)(i,j) = mat(bmap[i],bmap[j]);
                         }
 
                         for(j = 0; j < nint; ++j)
                         {
                             (*B)(i,j) = mat(bmap[i],imap[j]);
                         }
                     }
 
                     for(i = 0; i < nint; ++i)
                     {
                         for(j = 0; j < nbdry; ++j)
                         {
                             (*C)(i,j) = mat(imap[i],bmap[j]);
                         }
 
                         for(j = 0; j < nint; ++j)
                         {
                             (*D)(i,j) = mat(imap[i],imap[j]);
                         }
                     }
 
                     // Calculate static condensed system
                     if(nint)
                     {
                         D->Invert();
                         (*B) = (*B)*(*D);
                         (*A) = (*A) - (*B)*(*C);
                     }
 
                     DNekScalMatSharedPtr     Atmp;
 
                     returnval->SetBlock(0,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,A));
                     returnval->SetBlock(0,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(one,B));
                     returnval->SetBlock(1,0,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(factor,C));
                     returnval->SetBlock(1,1,Atmp = MemoryManager<DNekScalMat>::AllocateSharedPtr(invfactor,D));
 
                 }
             }
             return returnval;
         }

void Nektar::LocalRegions::HexExp::IProductWRTDerivBase_MatOp	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protected

Definition at line 490 of file HexExp.cpp.

References ASSERTL1, Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eIProductWRTDerivBase0, Nektar::StdRegions::eIProductWRTDerivBase1, Nektar::StdRegions::eIProductWRTDerivBase2, Nektar::StdRegions::StdExpansion::GetTotPoints(), m_matrixManager, and Nektar::StdRegions::StdExpansion::m_ncoeffs.

         { 
             int nq = GetTotPoints();            
             StdRegions::MatrixType mtype = StdRegions::eIProductWRTDerivBase0;
             
             switch(dir)
             {
             case 0:
                 {
                     mtype = StdRegions::eIProductWRTDerivBase0;
                 }
                 break;
             case 1:
                 {
                     mtype = StdRegions::eIProductWRTDerivBase1;
                 }
                 break;
             case 2:
                 {
                     mtype = StdRegions::eIProductWRTDerivBase2;
                 }
                 break;
             default:
                 {
                     ASSERTL1(false,"input dir is out of range");
                 }
                 break;
             }  
             
             MatrixKey      iprodmatkey(mtype,DetShapeType(),*this);
             DNekScalMatSharedPtr iprodmat = m_matrixManager[iprodmatkey];
             
             Blas::Dgemv('N',m_ncoeffs,nq,iprodmat->Scale(),(iprodmat->GetOwnedMatrix())->GetPtr().get(),
                         m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
         }

void Nektar::LocalRegions::HexExp::IProductWRTDerivBase_SumFac	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protected

Calculates the inner product 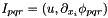$I_{pqr} = (u, \partial_{x_i} \phi_{pqr})$ .

The derivative of the basis functions is performed using the chain rule in order to incorporate the geometric factors. Assuming that the basis functions are a tensor product 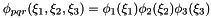$\phi_{pqr}(\xi_1,\xi_2,\xi_3) = \phi_1(\xi_1)\phi_2(\xi_2)\phi_3(\xi_3)$ , in the hexahedral element, this is straightforward and yields the result

$I_{pqr} = \sum_{k=1}^3 \left(u, \frac{\partial u}{\partial \xi_k} \frac{\partial \xi_k}{\partial x_i}\right)$

Parameters

dir	Direction in which to take the derivative.
inarray	The function .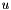
outarray	Value of the inner product.

Definition at line 428 of file HexExp.cpp.

References ASSERTL1, Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Nektar::StdRegions::StdExpansion::m_ncoeffs, Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric(), Vmath::Smul(), Vmath::Vadd(), and Vmath::Vmul().

Referenced by v_IProductWRTDerivBase().

         {   
             ASSERTL1((dir==0)||(dir==1)||(dir==2),"Invalid direction.");
 
             const int nq0 = m_base[0]->GetNumPoints();
             const int nq1 = m_base[1]->GetNumPoints();
             const int nq2 = m_base[2]->GetNumPoints();
             const int nq  = nq0*nq1*nq2;
             const int nm0 = m_base[0]->GetNumModes();
             const int nm1 = m_base[1]->GetNumModes();
  
             const Array<TwoD, const NekDouble>& df =
                                 m_metricinfo->GetDerivFactors(GetPointsKeys());
 
             Array<OneD, NekDouble> alloc(4*nq + m_ncoeffs + nm0*nq2*(nq1+nm1));
             Array<OneD, NekDouble> tmp1 (alloc);               // Quad metric
             Array<OneD, NekDouble> tmp2 (alloc +   nq);        // Dir1 metric
             Array<OneD, NekDouble> tmp3 (alloc + 2*nq);        // Dir2 metric
             Array<OneD, NekDouble> tmp4 (alloc + 3*nq);        // Dir3 metric
             Array<OneD, NekDouble> tmp5 (alloc + 4*nq);        // iprod tmp
             Array<OneD, NekDouble> wsp  (tmp5  +   m_ncoeffs); // Wsp
 
             MultiplyByQuadratureMetric(inarray, tmp1);
 
             if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
             {
                 Vmath::Vmul(nq,&df[3*dir][0],  1,tmp1.get(),1,tmp2.get(),1);
                 Vmath::Vmul(nq,&df[3*dir+1][0],1,tmp1.get(),1,tmp3.get(),1);
                 Vmath::Vmul(nq,&df[3*dir+2][0],1,tmp1.get(),1,tmp4.get(),1);
             }
             else
             {
                 Vmath::Smul(nq, df[3*dir][0],  tmp1.get(),1,tmp2.get(), 1);
                 Vmath::Smul(nq, df[3*dir+1][0],tmp1.get(),1,tmp3.get(), 1);
                 Vmath::Smul(nq, df[3*dir+2][0],tmp1.get(),1,tmp4.get(), 1);
             }  
             
             IProductWRTBase_SumFacKernel(m_base[0]->GetDbdata(),
                                          m_base[1]->GetBdata(),
                                          m_base[2]->GetBdata(),
                                          tmp2,outarray,wsp,
                                          false,true,true);
 
             IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
                                          m_base[1]->GetDbdata(),
                                          m_base[2]->GetBdata(),
                                          tmp3,tmp5,wsp,
                                          true,false,true);
             Vmath::Vadd(m_ncoeffs, tmp5, 1, outarray, 1, outarray, 1);
 
             IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
                                          m_base[1]->GetBdata(),
                                          m_base[2]->GetDbdata(),
                                          tmp4,tmp5,wsp,
                                          true,true,false);
             Vmath::Vadd(m_ncoeffs, tmp5, 1, outarray, 1, outarray, 1);
         }

void Nektar::LocalRegions::HexExp::v_ComputeFaceNormal ( const int face )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 799 of file HexExp.cpp.

References ASSERTL0, Nektar::StdRegions::StdExpansion::DetFaceBasisKey(), Nektar::SpatialDomains::eMovingRegular, Nektar::SpatialDomains::eRegular, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetCoordim(), Nektar::LocalRegions::Expansion::GetGeom(), Nektar::LibUtilities::BasisKey::GetNumPoints(), Nektar::LibUtilities::BasisKey::GetPointsKey(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::LibUtilities::Interp2D(), Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion3D::m_faceNormals, Vmath::Sdiv(), Vmath::Vmul(), Vmath::Vsqrt(), Vmath::Vvtvp(), and Vmath::Zero().

         {
             int i;
             const SpatialDomains::GeomFactorsSharedPtr & geomFactors =
                 GetGeom()->GetMetricInfo();
             SpatialDomains::GeomType type = geomFactors->GetGtype();
             LibUtilities::PointsKeyVector ptsKeys = GetPointsKeys();
             const Array<TwoD, const NekDouble> & df   = geomFactors->GetDerivFactors(ptsKeys);
             const Array<OneD, const NekDouble> & jac  = geomFactors->GetJac(ptsKeys);
 
             LibUtilities::BasisKey tobasis0 = DetFaceBasisKey(face,0);
             LibUtilities::BasisKey tobasis1 = DetFaceBasisKey(face,1);
 
             // Number of quadrature points in face expansion.
             int nq_face = tobasis0.GetNumPoints()*tobasis1.GetNumPoints();
 
             int vCoordDim = GetCoordim();
 
             m_faceNormals[face] = Array<OneD, Array<OneD, NekDouble> >(vCoordDim);
             Array<OneD, Array<OneD, NekDouble> > &normal = m_faceNormals[face];
             for (i = 0; i < vCoordDim; ++i)
             {
                 normal[i] = Array<OneD, NekDouble>(nq_face);
             }
             // Regular geometry case
             if((type == SpatialDomains::eRegular)||(type == SpatialDomains::eMovingRegular))
             {
                 NekDouble fac;
                 // Set up normals
                 switch(face)
                 {
                 case 0:
                     for(i = 0; i < vCoordDim; ++i)
                     {
                         normal[i][0] = -df[3*i+2][0]; 
                     }
                     break;
                 case 1:
                     for(i = 0; i < vCoordDim; ++i)
                     {
                         normal[i][0] = -df[3*i+1][0];
                     }
                     break;
                 case 2:
                     for(i = 0; i < vCoordDim; ++i)
                     {
                         normal[i][0] = df[3*i][0];
                     }
                     break;
                 case 3:
                     for(i = 0; i < vCoordDim; ++i)
                     {
                         normal[i][0] = df[3*i+1][0]; 
                     }
                     break;
                 case 4:
                     for(i = 0; i < vCoordDim; ++i)
                     {
                         normal[i][0] = -df[3*i][0]; 
                     }
                     break;
                 case 5:
                     for(i = 0; i < vCoordDim; ++i)
                     {
                         normal[i][0] = df[3*i+2][0]; 
                     }
                     break;
                 default:
                     ASSERTL0(false,"face is out of range (edge < 5)");
                 }
 
                 // normalise
                 fac = 0.0;
                 for(i =0 ; i < vCoordDim; ++i)
                 {
                     fac += normal[i][0]*normal[i][0];
                 }
                 fac = 1.0/sqrt(fac);
                 for (i = 0; i < vCoordDim; ++i)
                 {
                     Vmath::Fill(nq_face,fac*normal[i][0],normal[i],1);
                 }
         
             }
             else   // Set up deformed normals
             {
                 int j, k;
 
                 int nqe0 = m_base[0]->GetNumPoints();
                 int nqe1 = m_base[1]->GetNumPoints();
                 int nqe2 = m_base[2]->GetNumPoints();
                 int nqe01 = nqe0*nqe1;
                 int nqe02 = nqe0*nqe2;
                 int nqe12 = nqe1*nqe2;
                 
                 int nqe;
                 if (face == 0 || face == 5)
                 {
                     nqe = nqe01;
                 }
                 else if (face == 1 || face == 3)
                 {
                     nqe = nqe02;
                 }
                 else
                 {
                     nqe = nqe12;
                 }
                 
                 LibUtilities::PointsKey points0;
                 LibUtilities::PointsKey points1;
 
                 Array<OneD, NekDouble> faceJac(nqe);
                 Array<OneD, NekDouble> normals(vCoordDim*nqe,0.0);
 
                 // Extract Jacobian along face and recover local
                 // derivates (dx/dr) for polynomial interpolation by
                 // multiplying m_gmat by jacobian
                 switch(face)
                 {
                     case 0:
                         for(j = 0; j < nqe; ++j)
                         {
                             normals[j]       = -df[2][j]*jac[j];
                             normals[nqe+j]   = -df[5][j]*jac[j];
                             normals[2*nqe+j] = -df[8][j]*jac[j];
                             faceJac[j]       = jac[j];
                         }
 
                         points0 = ptsKeys[0];
                         points1 = ptsKeys[1];
                         break;
                     case 1:
                         for (j = 0; j < nqe0; ++j)
                         {
                             for(k = 0; k < nqe2; ++k)
                             {
                                 int idx = j + nqe01*k;
                                 normals[j+k*nqe0]       = -df[1][idx]*jac[idx];
                                 normals[nqe+j+k*nqe0]   = -df[4][idx]*jac[idx];
                                 normals[2*nqe+j+k*nqe0] = -df[7][idx]*jac[idx];
                                 faceJac[j+k*nqe0]       = jac[idx];
                             }
                         }
                         points0 = ptsKeys[0];
                         points1 = ptsKeys[2];
                         break;
                     case 2:
                         for (j = 0; j < nqe1; ++j)
                         {
                             for(k = 0; k < nqe2; ++k)
                             {
                                 int idx = nqe0-1+nqe0*j+nqe01*k;
                                 normals[j+k*nqe1]       = df[0][idx]*jac[idx];
                                 normals[nqe+j+k*nqe1]   = df[3][idx]*jac[idx];
                                 normals[2*nqe+j+k*nqe1] = df[6][idx]*jac[idx];
                                 faceJac[j+k*nqe1]       = jac[idx];
                             }
                         }
                         points0 = ptsKeys[1];
                         points1 = ptsKeys[2];
                         break;
                     case 3:
                         for (j = 0; j < nqe0; ++j)
                         {
                             for(k = 0; k < nqe2; ++k)
                             {
                                 int idx = nqe0*(nqe1-1)+j+nqe01*k;
                                 normals[j+k*nqe0]       = df[1][idx]*jac[idx];
                                 normals[nqe+j+k*nqe0]   = df[4][idx]*jac[idx];
                                 normals[2*nqe+j+k*nqe0] = df[7][idx]*jac[idx];
                                 faceJac[j+k*nqe0]       = jac[idx];
                             }
                         }
                         points0 = ptsKeys[0];
                         points1 = ptsKeys[2];
                         break;
                     case 4:
                         for (j = 0; j < nqe1; ++j)
                         {
                             for(k = 0; k < nqe2; ++k)
                             {
                                 int idx = j*nqe0+nqe01*k;
                                 normals[j+k*nqe1]       = -df[0][idx]*jac[idx];
                                 normals[nqe+j+k*nqe1]   = -df[3][idx]*jac[idx];
                                 normals[2*nqe+j+k*nqe1] = -df[6][idx]*jac[idx];
                                 faceJac[j+k*nqe1]       = jac[idx];
                             }
                         }
                         points0 = ptsKeys[1];
                         points1 = ptsKeys[2];
                         break;
                     case 5:
                         for (j = 0; j < nqe01; ++j)
                         {
                             int idx = j+nqe01*(nqe2-1);
                             normals[j]       = df[2][idx]*jac[idx];
                             normals[nqe+j]   = df[5][idx]*jac[idx];
                             normals[2*nqe+j] = df[8][idx]*jac[idx];
                             faceJac[j]       = jac[idx];
                         }
                         points0 = ptsKeys[0];
                         points1 = ptsKeys[1];
                         break;
                     default:
                     ASSERTL0(false,"face is out of range (face < 5)");
                 }
 
                 Array<OneD, NekDouble> work   (nq_face, 0.0);
                 // Interpolate Jacobian and invert
                 LibUtilities::Interp2D(points0, points1, faceJac,
                                        tobasis0.GetPointsKey(),
                                        tobasis1.GetPointsKey(),
                                        work);
 
                 Vmath::Sdiv(nq_face,1.0,&work[0],1,&work[0],1);
 
                 // interpolate
                 for(i = 0; i < GetCoordim(); ++i)
                 {
                     LibUtilities::Interp2D(points0, points1,
                                            &normals[i*nqe],
                                            tobasis0.GetPointsKey(),
                                            tobasis1.GetPointsKey(),
                                            &normal[i][0]);
                     Vmath::Vmul(nq_face,work,1,normal[i],1,normal[i],1);
                 }
 
                 //normalise normal vectors
                 Vmath::Zero(nq_face,work,1);
                 for(i = 0; i < GetCoordim(); ++i)
                 {
                     Vmath::Vvtvp(nq_face,normal[i],1, normal[i],1,work,1,work,1);
                 }
 
                 Vmath::Vsqrt(nq_face,work,1,work,1);
                 Vmath::Sdiv(nq_face,1.0,work,1,work,1);
 
                 for(i = 0; i < GetCoordim(); ++i)
                 {
                     Vmath::Vmul(nq_face,normal[i],1,work,1,normal[i],1);
                 }
             }
         }

void Nektar::LocalRegions::HexExp::v_ComputeLaplacianMetric ( )

protectedvirtual

Reimplemented from Nektar::LocalRegions::Expansion.

Definition at line 1828 of file HexExp.cpp.

         {
             if (m_metrics.count(eMetricQuadrature) == 0)
             {
                 ComputeQuadratureMetric();
             }
 
             const SpatialDomains::GeomType type = m_metricinfo->GetGtype();
             const unsigned int nqtot = GetTotPoints();
             const unsigned int dim = 3;
             const MetricType m[3][3] = { {eMetricLaplacian00, eMetricLaplacian01, eMetricLaplacian02},
                                        {eMetricLaplacian01, eMetricLaplacian11, eMetricLaplacian12},
                                        {eMetricLaplacian02, eMetricLaplacian12, eMetricLaplacian22}
             };
 
             for (unsigned int i = 0; i < dim; ++i)
             {
                 for (unsigned int j = i; j < dim; ++j)
                 {
                     m_metrics[m[i][j]] = Array<OneD, NekDouble>(nqtot);
                     const Array<TwoD, const NekDouble> &gmat =
                                  m_metricinfo->GetGmat(GetPointsKeys());
                     if (type == SpatialDomains::eDeformed)
                     {
                         Vmath::Vcopy(nqtot, &gmat[i*dim+j][0], 1,
                                             &m_metrics[m[i][j]][0], 1);
                     }
                     else
                     {
                         Vmath::Fill(nqtot, gmat[i*dim+j][0],
                                     &m_metrics[m[i][j]][0], 1);
                     }
                     MultiplyByQuadratureMetric(m_metrics[m[i][j]],
                                                m_metrics[m[i][j]]);
 
                 }
             }
         }

DNekMatSharedPtr Nektar::LocalRegions::HexExp::v_CreateStdMatrix ( const StdRegions::StdMatrixKey & mkey )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1294 of file HexExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             LibUtilities::BasisKey bkey0 = m_base[0]->GetBasisKey();
             LibUtilities::BasisKey bkey1 = m_base[1]->GetBasisKey();
             LibUtilities::BasisKey bkey2 = m_base[2]->GetBasisKey();
 
             StdRegions::StdHexExpSharedPtr tmp = MemoryManager<StdHexExp>
                                         ::AllocateSharedPtr(bkey0,bkey1,bkey2);
 
             return tmp->GetStdMatrix(mkey);
         }

LibUtilities::ShapeType Nektar::LocalRegions::HexExp::v_DetShapeType ( ) const

protectedvirtual

Return the region shape using the enum-list of ShapeType.

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 607 of file HexExp.cpp.

References Nektar::LibUtilities::eHexahedron.

         {
             return LibUtilities::eHexahedron;
         }

void Nektar::LocalRegions::HexExp::v_DropLocStaticCondMatrix ( const MatrixKey & mkey )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1759 of file HexExp.cpp.

References m_staticCondMatrixManager.

         {
             m_staticCondMatrixManager.DeleteObject(mkey);
         }

void Nektar::LocalRegions::HexExp::v_ExtractDataToCoeffs	(	const NekDouble *	data,
		const std::vector< unsigned int > &	nummodes,
		const int	nmode_offset,
		NekDouble *	coeffs
	)

protectedvirtual

Unpack data from input file assuming it comes from the same expansion type.

See also: StdExpansion::ExtractDataToCoeffs

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 613 of file HexExp.cpp.

References ASSERTL0, ASSERTL1, Nektar::LibUtilities::eModified_A, Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion::m_ncoeffs, Vmath::Vcopy(), and Vmath::Zero().

         {
             int data_order0 = nummodes[mode_offset];
             int fillorder0  = min(m_base[0]->GetNumModes(),data_order0);
             int data_order1 = nummodes[mode_offset+1];
             int order1      = m_base[1]->GetNumModes();
             int fillorder1  = min(order1,data_order1);
             int data_order2 = nummodes[mode_offset+2];
             int order2      = m_base[2]->GetNumModes();
             int fillorder2  = min(order2,data_order2);
 
             switch(m_base[0]->GetBasisType())
             {
             case LibUtilities::eModified_A:
                 {
                     int i,j;
                     int cnt  = 0;
                     int cnt1 = 0;
 
                     ASSERTL1(m_base[1]->GetBasisType() ==
                              LibUtilities::eModified_A,
                              "Extraction routine not set up for this basis");
                     ASSERTL1(m_base[2]->GetBasisType() ==
                              LibUtilities::eModified_A,
                              "Extraction routine not set up for this basis");
 
                     Vmath::Zero(m_ncoeffs,coeffs,1);
                     for(j = 0; j < fillorder0; ++j)
                     {
                         for(i = 0; i < fillorder1; ++i)
                         {
                             Vmath::Vcopy(fillorder2, &data[cnt],    1,
                                                      &coeffs[cnt1], 1);
                             cnt  += data_order2;
                             cnt1 += order2;
                         }
 
                         // count out data for j iteration
                         for(i = fillorder1; i < data_order1; ++i)
                         {
                             cnt += data_order2;
                         }
 
                         for(i = fillorder1; i < order1; ++i)
                         {
                             cnt1 += order2;
                         }
                     }
                 }
                 break;
             default:
                 ASSERTL0(false, "basis is either not set up or not "
                                 "hierarchicial");
             }
         }

void Nektar::LocalRegions::HexExp::v_FwdTrans	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Forward transform from physical quadrature space stored in inarray and evaluate the expansion coefficients and store in (this)->_coeffs.

Parameters

inarray	Input array
outarray	Output array

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 286 of file HexExp.cpp.

References Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eInvMass, Nektar::eWrapper, Nektar::StdRegions::StdExpansion::GetNcoeffs(), Nektar::StdRegions::StdExpansion::IProductWRTBase(), Nektar::StdRegions::StdExpansion::m_base, m_matrixManager, Nektar::StdRegions::StdExpansion::m_ncoeffs, and Vmath::Vcopy().

         {
             if( m_base[0]->Collocation() && m_base[1]->Collocation()
                     && m_base[2]->Collocation())
             {
                 Vmath::Vcopy(GetNcoeffs(),&inarray[0],1,&outarray[0],1);
             }
             else
             {
                 IProductWRTBase(inarray,outarray);
 
                 // get Mass matrix inverse
                 MatrixKey             masskey(StdRegions::eInvMass,
                                               DetShapeType(),*this);
                 DNekScalMatSharedPtr  matsys = m_matrixManager[masskey];
 
                 // copy inarray in case inarray == outarray
                 DNekVec in (m_ncoeffs,outarray);
                 DNekVec out(m_ncoeffs,outarray,eWrapper);
 
                 out = (*matsys)*in;
             }
         }

void Nektar::LocalRegions::HexExp::v_GeneralMatrixOp_MatOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1110 of file HexExp.cpp.

References Nektar::LocalRegions::Expansion::GetLocMatrix(), Nektar::StdRegions::StdExpansion::m_ncoeffs, and Vmath::Vcopy().

         {
             //int nConsts = mkey.GetNconstants();
             DNekScalMatSharedPtr   mat = GetLocMatrix(mkey);
 
 //            switch(nConsts)
 //            {
 //            case 0:
 //                {
 //                    mat = GetLocMatrix(mkey.GetMatrixType());
 //                }
 //                break;
 //            case 1:
 //                {
 //                    mat = GetLocMatrix(mkey.GetMatrixType(),mkey.GetConstant(0));
 //                }
 //                break;
 //            case 2:
 //                {
 //                    mat = GetLocMatrix(mkey.GetMatrixType(),mkey.GetConstant(0),mkey.GetConstant(1));
 //                }
 //                break;
 //
 //            default:
 //                {
 //                    NEKERROR(ErrorUtil::efatal, "Unknown number of constants");
 //                }
 //                break;
 //            }
 
             if(inarray.get() == outarray.get())
             {
                 Array<OneD,NekDouble> tmp(m_ncoeffs);
                 Vmath::Vcopy(m_ncoeffs,inarray.get(),1,tmp.get(),1);
 
                 Blas::Dgemv('N',m_ncoeffs,m_ncoeffs,mat->Scale(),(mat->GetOwnedMatrix())->GetPtr().get(),
                             m_ncoeffs, tmp.get(), 1, 0.0, outarray.get(), 1);
             }
             else
             {
                 Blas::Dgemv('N',m_ncoeffs,m_ncoeffs,mat->Scale(),(mat->GetOwnedMatrix())->GetPtr().get(),
                             m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
             }
         }

DNekMatSharedPtr Nektar::LocalRegions::HexExp::v_GenMatrix ( const StdRegions::StdMatrixKey & mkey )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1270 of file HexExp.cpp.

References Nektar::StdRegions::eHybridDGHelmBndLam, Nektar::StdRegions::eHybridDGHelmholtz, Nektar::StdRegions::eHybridDGLamToQ0, Nektar::StdRegions::eHybridDGLamToQ1, Nektar::StdRegions::eHybridDGLamToQ2, Nektar::StdRegions::eHybridDGLamToU, Nektar::StdRegions::eInvLaplacianWithUnityMean, Nektar::StdRegions::StdMatrixKey::GetMatrixType(), and Nektar::LocalRegions::Expansion3D::v_GenMatrix().

         {
             DNekMatSharedPtr returnval;
 
             switch(mkey.GetMatrixType())
             {
             case StdRegions::eHybridDGHelmholtz:
             case StdRegions::eHybridDGLamToU:
             case StdRegions::eHybridDGLamToQ0:
             case StdRegions::eHybridDGLamToQ1:
             case StdRegions::eHybridDGLamToQ2:
             case StdRegions::eHybridDGHelmBndLam:
             case StdRegions::eInvLaplacianWithUnityMean:
                 returnval = Expansion3D::v_GenMatrix(mkey);
                 break;
             default:
                 returnval = StdHexExp::v_GenMatrix(mkey);
             }
 
             return returnval;
         }

void Nektar::LocalRegions::HexExp::v_GetCoord	(	const Array< OneD, const NekDouble > &	Lcoords,
		Array< OneD, NekDouble > &	coords
	)

protectedvirtual

Retrieves the physical coordinates of a given set of reference coordinates.

Parameters

Lcoords	Local coordinates in reference space.
coords	Corresponding coordinates in physical space.

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 575 of file HexExp.cpp.

References ASSERTL1, and Nektar::LocalRegions::Expansion::m_geom.

         {
             int  i;
 
             ASSERTL1(Lcoords[0] >= -1.0 && Lcoords[0] <= 1.0 &&
                      Lcoords[1] >= -1.0 && Lcoords[1] <= 1.0 &&
                      Lcoords[2] >= -1.0 && Lcoords[2] <= 1.0,
                      "Local coordinates are not in region [-1,1]");
 
               m_geom->FillGeom();
 
             for(i = 0; i < m_geom->GetCoordim(); ++i)
             {
                 coords[i] = m_geom->GetCoord(i,Lcoords);
             }
         }

void Nektar::LocalRegions::HexExp::v_GetCoords	(	Array< OneD, NekDouble > &	coords_1,
		Array< OneD, NekDouble > &	coords_2,
		Array< OneD, NekDouble > &	coords_3
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 594 of file HexExp.cpp.

References Nektar::LocalRegions::Expansion::v_GetCoords().

         {
             Expansion::v_GetCoords(coords_0, coords_1, coords_2);
         }

bool Nektar::LocalRegions::HexExp::v_GetFaceDGForwards ( const int i ) const

protectedvirtual

Definition at line 673 of file HexExp.cpp.

References Nektar::StdRegions::eDir1BwdDir1_Dir2BwdDir2, Nektar::StdRegions::eDir1BwdDir2_Dir2FwdDir1, Nektar::StdRegions::eDir1FwdDir1_Dir2FwdDir2, Nektar::StdRegions::eDir1FwdDir2_Dir2BwdDir1, and Nektar::LocalRegions::Expansion3D::GetGeom3D().

         {
             StdRegions::Orientation fo = GetGeom3D()->GetForient(i);
             
             return fo == StdRegions::eDir1FwdDir1_Dir2FwdDir2 || 
                    fo == StdRegions::eDir1BwdDir1_Dir2BwdDir2 ||
                    fo == StdRegions::eDir1BwdDir2_Dir2FwdDir1 ||
                    fo == StdRegions::eDir1FwdDir2_Dir2BwdDir1;
         }

void Nektar::LocalRegions::HexExp::v_GetFacePhysMap	(	const int	face,
		Array< OneD, int > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 683 of file HexExp.cpp.

References ASSERTL0, and Nektar::StdRegions::StdExpansion::m_base.

         {
             int nquad0 = m_base[0]->GetNumPoints();
             int nquad1 = m_base[1]->GetNumPoints();
             int nquad2 = m_base[2]->GetNumPoints();
                         
             int nq0 = 0; 
             int nq1 = 0; 
 
             switch(face)
             {
                 case 0:
                     nq0 = nquad0;
                     nq1 = nquad1;
 
                     //Directions A and B positive
                     if(outarray.num_elements()!=nq0*nq1)
                     {
                         outarray = Array<OneD, int>(nq0*nq1);
                     }
 
                     for (int i = 0; i < nquad0*nquad1; ++i)
                     {
                         outarray[i] = i;
                     }
 
                     break;
                 case 1:
                     nq0 = nquad0;
                     nq1 = nquad2;
                     //Direction A and B positive
                     if(outarray.num_elements()!=nq0*nq1)
                     {
                         outarray = Array<OneD, int>(nq0*nq1);
                     }
                     
                     //Direction A and B positive
                     for (int k = 0; k < nquad2; k++)
                     {
                         for(int i = 0; i < nquad0; ++i)
                         {
                             outarray[k*nquad0 + i] = nquad0*nquad1*k + i;
                         }
                     }                    
                     break;
                 case 2:
                     nq0 = nquad1;
                     nq1 = nquad2;
                     
                     //Direction A and B positive
                     if(outarray.num_elements()!=nq0*nq1)
                     {
                         outarray = Array<OneD, int>(nq0*nq1);
                     }
                     
                     for (int i = 0; i < nquad1*nquad2; i++)
                     {
                         outarray[i] = nquad0-1 + i*nquad0;
                     }
                     break;
                 case 3:
                     nq0 = nquad0;
                     nq1 = nquad2;
                     
                     //Direction A and B positive
                     if(outarray.num_elements()!=nq0*nq1)
                     {
                         outarray = Array<OneD, int>(nq0*nq1);
                     }
 
                     for (int k = 0; k < nquad2; k++)
                     {
                         for (int i = 0; i < nquad0; i++)
                         {
                             outarray[k*nquad0 + i] = (nquad0*(nquad1-1))+(k*nquad0*nquad1) + i;
                         }
                     }                        
                     break;
                 case 4:
                     nq0 = nquad1;
                     nq1 = nquad2;
                     
                     //Direction A and B positive
                     if(outarray.num_elements()!=nq0*nq1)
                     {
                         outarray = Array<OneD, int>(nq0*nq1);
                     }
                     
                     for (int i = 0; i < nquad1*nquad2; i++)
                     {
                         outarray[i] = i*nquad0;
                     }                    
                     break;
                 case 5:
                     nq0 = nquad0;
                     nq1 = nquad1;
                     //Directions A and B positive
                     if(outarray.num_elements()!=nq0*nq1)
                     {
                         outarray = Array<OneD, int>(nq0*nq1);
                     }
 
                     for (int i = 0; i < nquad0*nquad1; i++)
                     {
                         outarray[i] = nquad0*nquad1*(nquad2-1) + i;
                     }
 
                     break;
                 default:
                     ASSERTL0(false,"face value (> 5) is out of range");
                     break;
             }
 
         }

DNekScalMatSharedPtr Nektar::LocalRegions::HexExp::v_GetLocMatrix ( const MatrixKey & mkey )

protectedvirtual

Reimplemented from Nektar::LocalRegions::Expansion.

Definition at line 1747 of file HexExp.cpp.

References m_matrixManager.

         {
             return m_matrixManager[mkey];
         }

DNekScalBlkMatSharedPtr Nektar::LocalRegions::HexExp::v_GetLocStaticCondMatrix ( const MatrixKey & mkey )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1753 of file HexExp.cpp.

References m_staticCondMatrixManager.

         {
             return m_staticCondMatrixManager[mkey];
         }

StdRegions::StdExpansionSharedPtr Nektar::LocalRegions::HexExp::v_GetStdExp ( void ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 559 of file HexExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             return MemoryManager<StdRegions::StdHexExp>
                 ::AllocateSharedPtr(m_base[0]->GetBasisKey(),
                                     m_base[1]->GetBasisKey(),
                                     m_base[2]->GetBasisKey());
         }

void Nektar::LocalRegions::HexExp::v_HelmholtzMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1101 of file HexExp.cpp.

References Nektar::StdRegions::StdExpansion3D::v_HelmholtzMatrixOp_MatFree().

         {
             HexExp::v_HelmholtzMatrixOp_MatFree(inarray,outarray,mkey);
         }

NekDouble Nektar::LocalRegions::HexExp::v_Integral ( const Array< OneD, const NekDouble > & inarray )

protectedvirtual

Integrate the physical point list inarray over region.

Parameters

inarray definition of function to be returned at quadrature points of expansion.

Returns: $\int^1_{-1}\int^1_{-1} \int^1_{-1} u(\eta_1, \eta_2, \eta_3) J[i,j,k] d \eta_1 d \eta_2 d \eta_3$ where $inarray[i,j,k] = u(\eta_{1i},\eta_{2j},\eta_{3k})$ and is the Jacobian evaluated at the quadrature point.

Reimplemented from Nektar::StdRegions::StdExpansion3D.

Definition at line 114 of file HexExp.cpp.

References Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Smul(), and Vmath::Vmul().

         {
             int    nquad0 = m_base[0]->GetNumPoints();
             int    nquad1 = m_base[1]->GetNumPoints();
             int    nquad2 = m_base[2]->GetNumPoints();
             Array<OneD, const NekDouble> jac = m_metricinfo->GetJac(GetPointsKeys());
             NekDouble returnVal;
             Array<OneD,NekDouble> tmp(nquad0*nquad1*nquad2);
 
             // multiply inarray with Jacobian
 
             if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
             {
                 Vmath::Vmul(nquad0*nquad1*nquad2,&jac[0],1,
                             (NekDouble*)&inarray[0],1,&tmp[0],1);
             }
             else
             {
                 Vmath::Smul(nquad0*nquad1*nquad2,(NekDouble) jac[0],
                             (NekDouble*)&inarray[0],1,&tmp[0],1);
             }
 
             // call StdHexExp version;
             returnVal = StdHexExp::v_Integral(tmp);
 
             return  returnVal;
         }

void Nektar::LocalRegions::HexExp::v_IProductWRTBase	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Calculate the inner product of inarray with respect to the elements basis.

Parameters

inarray	Input array of physical space data.
outarray	Output array of data.

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 324 of file HexExp.cpp.

References v_IProductWRTBase_SumFac().

         {
             HexExp::v_IProductWRTBase_SumFac(inarray, outarray);
         }

void Nektar::LocalRegions::HexExp::v_IProductWRTBase_SumFac	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		bool	multiplybyweights = `true`
	)

protectedvirtual

Calculate the inner product of inarray with respect to the given basis B = base0 * base1 * base2.

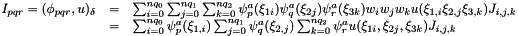
$\begin{array}{rcl} I_{pqr} = (\phi_{pqr}, u)_{\delta} & = & \sum_{i=0}^{nq_0} \sum_{j=0}^{nq_1} \sum_{k=0}^{nq_2} \psi_{p}^{a} (\xi_{1i}) \psi_{q}^{a} (\xi_{2j}) \psi_{r}^{a} (\xi_{3k}) w_i w_j w_k u(\xi_{1,i} \xi_{2,j} \xi_{3,k}) J_{i,j,k}\\ & = & \sum_{i=0}^{nq_0} \psi_p^a(\xi_{1,i}) \sum_{j=0}^{nq_1} \psi_{q}^a(\xi_{2,j}) \sum_{k=0}^{nq_2} \psi_{r}^a u(\xi_{1i},\xi_{2j},\xi_{3k}) J_{i,j,k} \end{array}$
where 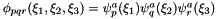$\phi_{pqr} (\xi_1 , \xi_2 , \xi_3) = \psi_p^a ( \xi_1) \psi_{q}^a (\xi_2) \psi_{r}^a (\xi_3)$
which can be implemented as
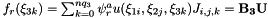
$f_{r} (\xi_{3k}) = \sum_{k=0}^{nq_3} \psi_{r}^a u(\xi_{1i},\xi_{2j},\xi_{3k}) J_{i,j,k} = {\bf B_3 U}$
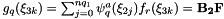
$g_{q} (\xi_{3k}) = \sum_{j=0}^{nq_1} \psi_{q}^a (\xi_{2j}) f_{r} (\xi_{3k}) = {\bf B_2 F}$
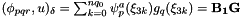
$(\phi_{pqr}, u)_{\delta} = \sum_{k=0}^{nq_0} \psi_{p}^a (\xi_{3k}) g_{q} (\xi_{3k}) = {\bf B_1 G}$

Parameters

base0	Basis to integrate wrt in first dimension.
base1	Basis to integrate wrt in second dimension.
base2	Basis to integrate wrt in third dimension.
inarray	Input array.
outarray	Output array.
coll_check	(not used)

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 363 of file HexExp.cpp.

References Nektar::StdRegions::StdExpansion3D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, and Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric().

Referenced by v_IProductWRTBase().

         {
             int    nquad0 = m_base[0]->GetNumPoints();
             int    nquad1 = m_base[1]->GetNumPoints();
             int    nquad2 = m_base[2]->GetNumPoints();
             int    order0 = m_base[0]->GetNumModes();
             int    order1 = m_base[1]->GetNumModes();
 
             Array<OneD, NekDouble> wsp(nquad0*nquad1*(nquad2+order0) +
                                        order0*order1*nquad2);
 
             if(multiplybyweights)
             {
                 Array<OneD, NekDouble> tmp(inarray.num_elements());
 
                 MultiplyByQuadratureMetric(inarray, tmp);
                IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
                                              m_base[1]->GetBdata(),
                                              m_base[2]->GetBdata(),
                                              tmp,outarray,wsp,
                                              true,true,true);
             }
             else
             {
                IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
                                             m_base[1]->GetBdata(),
                                             m_base[2]->GetBdata(),
                                             inarray,outarray,wsp,
                                             true,true,true);
 
             }
         }

void Nektar::LocalRegions::HexExp::v_IProductWRTDerivBase	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 399 of file HexExp.cpp.

References IProductWRTDerivBase_SumFac().

         {
             HexExp::IProductWRTDerivBase_SumFac(dir,inarray,outarray);
         }

void Nektar::LocalRegions::HexExp::v_LaplacianMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1055 of file HexExp.cpp.

References Nektar::StdRegions::StdExpansion3D::v_LaplacianMatrixOp_MatFree().

         {
             HexExp::v_LaplacianMatrixOp_MatFree(inarray,outarray,mkey);
         }

void Nektar::LocalRegions::HexExp::v_LaplacianMatrixOp	(	const int	k1,
		const int	k2,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1063 of file HexExp.cpp.

         {
             StdExpansion::LaplacianMatrixOp_MatFree(k1,k2,inarray,outarray,
                                                         mkey);
         }

void Nektar::LocalRegions::HexExp::v_LaplacianMatrixOp_MatFree_Kernel	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		Array< OneD, NekDouble > &	wsp
	)

privatevirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1764 of file HexExp.cpp.

         {
             // This implementation is only valid when there are no
             // coefficients associated to the Laplacian operator
             if (m_metrics.count(eMetricLaplacian00) == 0)
             {
                 ComputeLaplacianMetric();
             }
 
             int       nquad0  = m_base[0]->GetNumPoints();
             int       nquad1  = m_base[1]->GetNumPoints();
             int       nquad2  = m_base[2]->GetNumPoints();
             int       nqtot   = nquad0*nquad1*nquad2;
 
             ASSERTL1(wsp.num_elements() >= 6*nqtot,
                      "Insufficient workspace size.");
 
             const Array<OneD, const NekDouble>& base0  = m_base[0]->GetBdata();
             const Array<OneD, const NekDouble>& base1  = m_base[1]->GetBdata();
             const Array<OneD, const NekDouble>& base2  = m_base[2]->GetBdata();
             const Array<OneD, const NekDouble>& dbase0 = m_base[0]->GetDbdata();
             const Array<OneD, const NekDouble>& dbase1 = m_base[1]->GetDbdata();
             const Array<OneD, const NekDouble>& dbase2 = m_base[2]->GetDbdata();
             const Array<OneD, const NekDouble>& metric00 = m_metrics[eMetricLaplacian00];
             const Array<OneD, const NekDouble>& metric01 = m_metrics[eMetricLaplacian01];
             const Array<OneD, const NekDouble>& metric02 = m_metrics[eMetricLaplacian02];
             const Array<OneD, const NekDouble>& metric11 = m_metrics[eMetricLaplacian11];
             const Array<OneD, const NekDouble>& metric12 = m_metrics[eMetricLaplacian12];
             const Array<OneD, const NekDouble>& metric22 = m_metrics[eMetricLaplacian22];
 
             // Allocate temporary storage
             Array<OneD,NekDouble> wsp0(wsp);
             Array<OneD,NekDouble> wsp1(wsp+1*nqtot);
             Array<OneD,NekDouble> wsp2(wsp+2*nqtot);
             Array<OneD,NekDouble> wsp3(wsp+3*nqtot);
             Array<OneD,NekDouble> wsp4(wsp+4*nqtot);
             Array<OneD,NekDouble> wsp5(wsp+5*nqtot);
 
             StdExpansion3D::PhysTensorDeriv(inarray,wsp0,wsp1,wsp2);
 
             // wsp0 = k = g0 * wsp1 + g1 * wsp2 = g0 * du_dxi1 + g1 * du_dxi2
             // wsp2 = l = g1 * wsp1 + g2 * wsp2 = g0 * du_dxi1 + g1 * du_dxi2
             // where g0, g1 and g2 are the metric terms set up in the GeomFactors class
             // especially for this purpose
             Vmath::Vvtvvtp(nqtot,&metric00[0],1,&wsp0[0],1,&metric01[0],1,&wsp1[0],1,&wsp3[0],1);
             Vmath::Vvtvp  (nqtot,&metric02[0],1,&wsp2[0],1,&wsp3[0],1,&wsp3[0],1);
             Vmath::Vvtvvtp(nqtot,&metric01[0],1,&wsp0[0],1,&metric11[0],1,&wsp1[0],1,&wsp4[0],1);
             Vmath::Vvtvp  (nqtot,&metric12[0],1,&wsp2[0],1,&wsp4[0],1,&wsp4[0],1);
             Vmath::Vvtvvtp(nqtot,&metric02[0],1,&wsp0[0],1,&metric12[0],1,&wsp1[0],1,&wsp5[0],1);
             Vmath::Vvtvp  (nqtot,&metric22[0],1,&wsp2[0],1,&wsp5[0],1,&wsp5[0],1);
 
             // outarray = m = (D_xi1 * B)^T * k
             // wsp1     = n = (D_xi2 * B)^T * l
             IProductWRTBase_SumFacKernel(dbase0,base1,base2,wsp3,outarray,wsp0,false,true,true);
             IProductWRTBase_SumFacKernel(base0,dbase1,base2,wsp4,wsp2,    wsp0,true,false,true);
             Vmath::Vadd(m_ncoeffs,wsp2.get(),1,outarray.get(),1,outarray.get(),1);
             IProductWRTBase_SumFacKernel(base0,base1,dbase2,wsp5,wsp2,    wsp0,true,true,false);
             Vmath::Vadd(m_ncoeffs,wsp2.get(),1,outarray.get(),1,outarray.get(),1);
         }

void Nektar::LocalRegions::HexExp::v_MassLevelCurvatureMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1092 of file HexExp.cpp.

         {
             StdExpansion::MassLevelCurvatureMatrixOp_MatFree(inarray,
                                                                 outarray,mkey);
         }

void Nektar::LocalRegions::HexExp::v_MassMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1047 of file HexExp.cpp.

         {
             StdExpansion::MassMatrixOp_MatFree(inarray,outarray,mkey);
         }

void Nektar::LocalRegions::HexExp::v_PhysDeriv	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	out_d0,
		Array< OneD, NekDouble > &	out_d1,
		Array< OneD, NekDouble > &	out_d2
	)

protectedvirtual

Calculate the derivative of the physical points.

For Hexahedral region can use the Tensor_Deriv function defined under StdExpansion.

Parameters

inarray	Input array
out_d0	Derivative of inarray in first direction.
out_d1	Derivative of inarray in second direction.
out_d2	Derivative of inarray in third direction.

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 157 of file HexExp.cpp.

References Nektar::SpatialDomains::eDeformed, Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::m_base, Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Smul(), Vmath::Vmul(), and Vmath::Vvtvp().

         {
             int    nquad0 = m_base[0]->GetNumPoints();
             int    nquad1 = m_base[1]->GetNumPoints();
             int    nquad2 = m_base[2]->GetNumPoints();
             int    ntot   = nquad0 * nquad1 * nquad2;
 
             Array<TwoD, const NekDouble> df =
                                 m_metricinfo->GetDerivFactors(GetPointsKeys());
             Array<OneD,NekDouble> Diff0 = Array<OneD,NekDouble>(ntot);
             Array<OneD,NekDouble> Diff1 = Array<OneD,NekDouble>(ntot);
             Array<OneD,NekDouble> Diff2 = Array<OneD,NekDouble>(ntot);
 
             StdHexExp::v_PhysDeriv(inarray, Diff0, Diff1, Diff2);
 
             if(m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
             {
                 if(out_d0.num_elements())
                 {
                     Vmath::Vmul (ntot,&df[0][0],1,&Diff0[0],1, &out_d0[0], 1);
                     Vmath::Vvtvp(ntot,&df[1][0],1,&Diff1[0],1, &out_d0[0], 1,
                                                                  &out_d0[0],1);
                     Vmath::Vvtvp(ntot,&df[2][0],1,&Diff2[0],1, &out_d0[0], 1,
                                                                  &out_d0[0],1);
                 }
 
                 if(out_d1.num_elements())
                 {
                     Vmath::Vmul (ntot,&df[3][0],1,&Diff0[0],1, &out_d1[0], 1);
                     Vmath::Vvtvp(ntot,&df[4][0],1,&Diff1[0],1, &out_d1[0], 1,
                                                                  &out_d1[0],1);
                     Vmath::Vvtvp(ntot,&df[5][0],1,&Diff2[0],1, &out_d1[0], 1,
                                                                  &out_d1[0],1);
                 }
 
                 if(out_d2.num_elements())
                 {
                     Vmath::Vmul (ntot,&df[6][0],1,&Diff0[0],1, &out_d2[0], 1);
                     Vmath::Vvtvp(ntot,&df[7][0],1,&Diff1[0],1, &out_d2[0], 1,
                                                                  &out_d2[0],1);
                     Vmath::Vvtvp(ntot,&df[8][0],1,&Diff2[0],1, &out_d2[0], 1,
                                                                  &out_d2[0],1);
                 }
             }
             else // regular geometry
             {
                 if(out_d0.num_elements())
                 {
                     Vmath::Smul (ntot,df[0][0],&Diff0[0],1, &out_d0[0], 1);
                     Blas::Daxpy (ntot,df[1][0],&Diff1[0],1, &out_d0[0], 1);
                     Blas::Daxpy (ntot,df[2][0],&Diff2[0],1, &out_d0[0], 1);
                 }
 
                 if(out_d1.num_elements())
                 {
                     Vmath::Smul (ntot,df[3][0],&Diff0[0],1, &out_d1[0], 1);
                     Blas::Daxpy (ntot,df[4][0],&Diff1[0],1, &out_d1[0], 1);
                     Blas::Daxpy (ntot,df[5][0],&Diff2[0],1, &out_d1[0], 1);
                 }
 
                 if(out_d2.num_elements())
                 {
                     Vmath::Smul (ntot,df[6][0],&Diff0[0],1, &out_d2[0], 1);
                     Blas::Daxpy (ntot,df[7][0],&Diff1[0],1, &out_d2[0], 1);
                     Blas::Daxpy (ntot,df[8][0],&Diff2[0],1, &out_d2[0], 1);
                 }
             }
         }

void Nektar::LocalRegions::HexExp::v_PhysDeriv	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Calculate the derivative of the physical points in a single direction.

Parameters

dir	Direction in which to compute derivative. Valid values are 0, 1, 2.
inarray	Input array.
outarray	Output array.

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 240 of file HexExp.cpp.

References ASSERTL1, Nektar::NullNekDouble1DArray, and Nektar::StdRegions::StdExpansion::PhysDeriv().

         {
             switch(dir)
             {
             case 0:
                 {
                     PhysDeriv(inarray, outarray, NullNekDouble1DArray,
                               NullNekDouble1DArray);
                 }
                 break;
             case 1:
                 {
                     PhysDeriv(inarray, NullNekDouble1DArray, outarray,
                               NullNekDouble1DArray);
                 }
                 break;
             case 2:
                 {
                     PhysDeriv(inarray, NullNekDouble1DArray,
                               NullNekDouble1DArray, outarray);
                 }
                 break;
             default:
                 {
                     ASSERTL1(false,"input dir is out of range");
                 }
                 break;
             }
         }

NekDouble Nektar::LocalRegions::HexExp::v_PhysEvaluate	(	const Array< OneD, const NekDouble > &	coords,
		const Array< OneD, const NekDouble > &	physvals
	)

protectedvirtual

This function evaluates the expansion at a single (arbitrary) point of the domain.

Based on the value of the expansion at the quadrature points, this function calculates the value of the expansion at an arbitrary single points (with coordinates 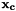$\mathbf{x_c}$ given by the pointer coords). This operation, equivalent to

$u(\mathbf{x_c}) = \sum_p \phi_p(\mathbf{x_c}) \hat{u}_p$

is evaluated using Lagrangian interpolants through the quadrature points:

$u(\mathbf{x_c}) = \sum_p h_p(\mathbf{x_c}) u_p$

This function requires that the physical value array $\mathbf{u}$ (implemented as the attribute #phys) is set.

Parameters

coords the coordinates of the single point

Returns: returns the value of the expansion at the single point

Reimplemented from Nektar::StdRegions::StdExpansion3D.

Definition at line 548 of file HexExp.cpp.

References ASSERTL0, and Nektar::LocalRegions::Expansion::m_geom.

         {
             Array<OneD,NekDouble> Lcoord = Array<OneD,NekDouble>(3);
 
             ASSERTL0(m_geom,"m_geom not defined");
             m_geom->GetLocCoords(coord,Lcoord);
             return StdHexExp::v_PhysEvaluate(Lcoord, physvals);
         }

void Nektar::LocalRegions::HexExp::v_ReduceOrderCoeffs	(	int	numMin,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

This function is used to compute exactly the advective numerical flux on the interface of two elements with different expansions, hence an appropriate number of Gauss points has to be used. The number of Gauss points has to be equal to the number used by the highest polynomial degree of the two adjacent elements

Parameters

numMin	Is the reduced polynomial order
inarray	Input array of coefficients
dumpVar	Output array of reduced coefficients.

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1169 of file HexExp.cpp.

References Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::eOrtho_A, Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::LibUtilities::InterpCoeff3D(), Nektar::StdRegions::StdExpansion::m_base, Vmath::Vcopy(), and Vmath::Zero().

         {
             int n_coeffs = inarray.num_elements();
             int nmodes0  = m_base[0]->GetNumModes();
             int nmodes1  = m_base[1]->GetNumModes();
             int nmodes2  = m_base[2]->GetNumModes();
             int numMax   = nmodes0;
 
             Array<OneD, NekDouble> coeff     (n_coeffs);
             Array<OneD, NekDouble> coeff_tmp1(nmodes0*nmodes1, 0.0);
             Array<OneD, NekDouble> coeff_tmp2(n_coeffs,        0.0);
             Array<OneD, NekDouble> tmp, tmp2, tmp3, tmp4;
 
             Vmath::Vcopy(n_coeffs,inarray,1,coeff_tmp2,1);
 
             const LibUtilities::PointsKey Pkey0(
                 nmodes0, LibUtilities::eGaussLobattoLegendre);
             const LibUtilities::PointsKey Pkey1(
                 nmodes1, LibUtilities::eGaussLobattoLegendre);
             const LibUtilities::PointsKey Pkey2(
                 nmodes2, LibUtilities::eGaussLobattoLegendre);
 
             LibUtilities::BasisKey b0(
                 m_base[0]->GetBasisType(), nmodes0, Pkey0);
             LibUtilities::BasisKey b1(
                 m_base[1]->GetBasisType(), nmodes1, Pkey1);
             LibUtilities::BasisKey b2(
                 m_base[2]->GetBasisType(), nmodes2, Pkey2);
             LibUtilities::BasisKey bortho0(
                 LibUtilities::eOrtho_A,    nmodes0, Pkey0);
             LibUtilities::BasisKey bortho1(
                 LibUtilities::eOrtho_A,    nmodes1, Pkey1);
             LibUtilities::BasisKey bortho2(
                 LibUtilities::eOrtho_A,    nmodes2, Pkey2);
 
             LibUtilities::InterpCoeff3D(
                 b0,      b1,      b2,      coeff_tmp2,
                 bortho0, bortho1, bortho2, coeff);
 
             Vmath::Zero(n_coeffs, coeff_tmp2, 1);
 
             int cnt = 0, cnt2 = 0;
 
             for (int u = 0; u < numMin+1; ++u)
             {
                 for (int i = 0; i < numMin; ++i)
                 {
                     Vmath::Vcopy(numMin,
                                  tmp  = coeff+cnt+cnt2,1,
                                  tmp2 = coeff_tmp1+cnt,1);
 
                     cnt = i*numMax;
                 }
 
                 Vmath::Vcopy(nmodes0*nmodes1,
                              tmp3 = coeff_tmp1,1,
                              tmp4 = coeff_tmp2+cnt2,1);
 
                 cnt2 = u*nmodes0*nmodes1;
             }
 
             LibUtilities::InterpCoeff3D(
                 bortho0, bortho1, bortho2, coeff_tmp2,
                 b0,      b1,      b2,      outarray);
         }

NekDouble Nektar::LocalRegions::HexExp::v_StdPhysEvaluate	(	const Array< OneD, const NekDouble > &	Lcoord,
		const Array< OneD, const NekDouble > &	physvals
	)

protectedvirtual

Given the local cartesian coordinate Lcoord evaluate the value of physvals at this point by calling through to the StdExpansion method

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 540 of file HexExp.cpp.

         {
             // Evaluate point in local coordinates.
             return StdHexExp::v_PhysEvaluate(Lcoord,physvals);
         }

void Nektar::LocalRegions::HexExp::v_SVVLaplacianFilter	(	Array< OneD, NekDouble > &	array,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1238 of file HexExp.cpp.

References Nektar::SpatialDomains::eDeformed, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetPointsKeys(), Nektar::StdRegions::StdExpansion::GetTotPoints(), Nektar::LocalRegions::Expansion::m_metricinfo, Vmath::Vdiv(), Vmath::Vmul(), and Vmath::Vsqrt().

         {
             int nq = GetTotPoints();
             
             // Calculate sqrt of the Jacobian
             Array<OneD, const NekDouble> jac = 
                                     m_metricinfo->GetJac(GetPointsKeys());
             Array<OneD, NekDouble> sqrt_jac(nq);
             if (m_metricinfo->GetGtype() == SpatialDomains::eDeformed)
             {
                 Vmath::Vsqrt(nq,jac,1,sqrt_jac,1);
             }
             else
             {
                 Vmath::Fill(nq,sqrt(jac[0]),sqrt_jac,1);
             }
             
             // Multiply array by sqrt(Jac)
             Vmath::Vmul(nq,sqrt_jac,1,array,1,array,1);
             
             // Apply std region filter
             StdHexExp::v_SVVLaplacianFilter( array, mkey);
             
             // Divide by sqrt(Jac)
             Vmath::Vdiv(nq,array,1,sqrt_jac,1,array,1);
         }

void Nektar::LocalRegions::HexExp::v_WeakDerivMatrixOp	(	const int	i,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdHexExp.

Definition at line 1074 of file HexExp.cpp.

         {
             StdExpansion::WeakDerivMatrixOp_MatFree(i,inarray,outarray,mkey);
         }

void Nektar::LocalRegions::HexExp::v_WeakDirectionalDerivMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdRegions::StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1083 of file HexExp.cpp.

         {
             StdExpansion::WeakDirectionalDerivMatrixOp_MatFree(inarray,
                                                                 outarray,mkey);
         }

Member Data Documentation

LibUtilities::NekManager<MatrixKey, DNekScalMat, MatrixKey::opLess> Nektar::LocalRegions::HexExp::m_matrixManager

private

Definition at line 261 of file HexExp.h.

Referenced by CreateMatrix(), IProductWRTDerivBase_MatOp(), v_FwdTrans(), and v_GetLocMatrix().

LibUtilities::NekManager<MatrixKey, DNekScalBlkMat, MatrixKey::opLess> Nektar::LocalRegions::HexExp::m_staticCondMatrixManager

private

Definition at line 262 of file HexExp.h.

Referenced by v_DropLocStaticCondMatrix(), and v_GetLocStaticCondMatrix().

Public Member Functions

Protected Member Functions

Private Member Functions

Private Attributes

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation