#include <StdTriExp.h>

Inheritance diagram for Nektar::StdRegions::StdTriExp:

Collaboration diagram for Nektar::StdRegions::StdTriExp:

Public Member Functions
	StdTriExp ()

	StdTriExp (const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb)

	StdTriExp (const StdTriExp &T)

	~StdTriExp ()

Public Member Functions inherited from Nektar::StdRegions::StdExpansion2D
	StdExpansion2D ()

	StdExpansion2D (int numcoeffs, const LibUtilities::BasisKey &Ba, const LibUtilities::BasisKey &Bb)

	StdExpansion2D (const StdExpansion2D &T)

virtual	~StdExpansion2D ()

void	PhysTensorDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray_d0, Array< OneD, NekDouble > &outarray_d1)
	Calculate the 2D derivative in the local tensor/collapsed coordinate at the physical points. More...

NekDouble	Integral (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &w0, const Array< OneD, const NekDouble > &w1)

void	BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0=true, bool doCheckCollDir1=true)

void	IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0=true, bool doCheckCollDir1=true)

Public Member Functions inherited from Nektar::StdRegions::StdExpansion
	StdExpansion ()
	Default Constructor. More...

	StdExpansion (const int numcoeffs, const int numbases, const LibUtilities::BasisKey &Ba=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bb=LibUtilities::NullBasisKey, const LibUtilities::BasisKey &Bc=LibUtilities::NullBasisKey)
	Constructor. More...

	StdExpansion (const StdExpansion &T)
	Copy Constructor. More...

virtual	~StdExpansion ()
	Destructor. More...

int	GetNumBases () const
	This function returns the number of 1D bases used in the expansion. More...

const Array< OneD, const LibUtilities::BasisSharedPtr > &	GetBase () const
	This function gets the shared point to basis. More...

const LibUtilities::BasisSharedPtr &	GetBasis (int dir) const
	This function gets the shared point to basis in the dir direction. More...

int	GetNcoeffs (void) const
	This function returns the total number of coefficients used in the expansion. More...

int	GetTotPoints () const
	This function returns the total number of quadrature points used in the element. More...

LibUtilities::BasisType	GetBasisType (const int dir) const
	This function returns the type of basis used in the dir direction. More...

int	GetBasisNumModes (const int dir) const
	This function returns the number of expansion modes in the dir direction. More...

int	EvalBasisNumModesMax (void) const
	This function returns the maximum number of expansion modes over all local directions. More...

LibUtilities::PointsType	GetPointsType (const int dir) const
	This function returns the type of quadrature points used in the dir direction. More...

int	GetNumPoints (const int dir) const
	This function returns the number of quadrature points in the dir direction. More...

const Array< OneD, const NekDouble > &	GetPoints (const int dir) const
	This function returns a pointer to the array containing the quadrature points in dir direction. More...

int	GetNverts () const
	This function returns the number of vertices of the expansion domain. More...

int	GetNedges () const
	This function returns the number of edges of the expansion domain. More...

int	GetEdgeNcoeffs (const int i) const
	This function returns the number of expansion coefficients belonging to the i-th edge. More...

int	GetTotalEdgeIntNcoeffs () const

int	GetEdgeNumPoints (const int i) const
	This function returns the number of quadrature points belonging to the i-th edge. More...

int	DetCartesianDirOfEdge (const int edge)

const LibUtilities::BasisKey	DetEdgeBasisKey (const int i) const

const LibUtilities::BasisKey	DetFaceBasisKey (const int i, const int k) const

int	GetFaceNumPoints (const int i) const
	This function returns the number of quadrature points belonging to the i-th face. More...

int	GetFaceNcoeffs (const int i) const
	This function returns the number of expansion coefficients belonging to the i-th face. More...

int	GetFaceIntNcoeffs (const int i) const

int	GetTotalFaceIntNcoeffs () const

int	GetTraceNcoeffs (const int i) const
	This function returns the number of expansion coefficients belonging to the i-th edge/face. More...

LibUtilities::PointsKey	GetFacePointsKey (const int i, const int j) const

int	NumBndryCoeffs (void) const

int	NumDGBndryCoeffs (void) const

LibUtilities::BasisType	GetEdgeBasisType (const int i) const
	This function returns the type of expansion basis on the i-th edge. More...

const LibUtilities::PointsKey	GetNodalPointsKey () const
	This function returns the type of expansion Nodal point type if defined. More...

int	GetNfaces () const
	This function returns the number of faces of the expansion domain. More...

int	GetNtrace () const
	Returns the number of trace elements connected to this element. More...

LibUtilities::ShapeType	DetShapeType () const
	This function returns the shape of the expansion domain. More...

boost::shared_ptr< StdExpansion >	GetStdExp (void) const

int	GetShapeDimension () const

bool	IsBoundaryInteriorExpansion ()

bool	IsNodalNonTensorialExp ()

void	BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	This function performs the Backward transformation from coefficient space to physical space. More...

void	FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	This function performs the Forward transformation from physical space to coefficient space. More...

void	FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

NekDouble	Integral (const Array< OneD, const NekDouble > &inarray)
	This function integrates the specified function over the domain. More...

void	FillMode (const int mode, Array< OneD, NekDouble > &outarray)
	This function fills the array outarray with the mode-th mode of the expansion. More...

void	IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	this function calculates the inner product of a given function f with the different modes of the expansion More...

void	IProductWRTBase (const Array< OneD, const NekDouble > &base, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, int coll_check)

void	IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

int	GetElmtId ()
	Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...

void	SetElmtId (const int id)
	Set the element id of this expansion when used in a list by returning value of m_elmt_id. More...

void	GetCoords (Array< OneD, NekDouble > &coords_1, Array< OneD, NekDouble > &coords_2=NullNekDouble1DArray, Array< OneD, NekDouble > &coords_3=NullNekDouble1DArray)
	this function returns the physical coordinates of the quadrature points of the expansion More...

void	GetCoord (const Array< OneD, const NekDouble > &Lcoord, Array< OneD, NekDouble > &coord)
	given the coordinates of a point of the element in the local collapsed coordinate system, this function calculates the physical coordinates of the point More...

DNekMatSharedPtr	GetStdMatrix (const StdMatrixKey &mkey)

DNekBlkMatSharedPtr	GetStdStaticCondMatrix (const StdMatrixKey &mkey)

IndexMapValuesSharedPtr	GetIndexMap (const IndexMapKey &ikey)

const Array< OneD, const NekDouble > &	GetPhysNormals (void)

void	SetPhysNormals (Array< OneD, const NekDouble > &normal)

virtual void	SetUpPhysNormals (const int edge)

void	NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, Array< OneD, NekDouble > &outarray)

void	NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, NekDouble > &Fy, Array< OneD, NekDouble > &outarray)

void	NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)

void	NormVectorIProductWRTBase (const Array< OneD, const Array< OneD, NekDouble > > &Fvec, Array< OneD, NekDouble > &outarray)

DNekScalBlkMatSharedPtr	GetLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)

void	DropLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)

StdRegions::Orientation	GetForient (int face)

StdRegions::Orientation	GetEorient (int edge)

StdRegions::Orientation	GetPorient (int point)

StdRegions::Orientation	GetCartesianEorient (int edge)

void	SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)

void	SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

int	CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)

void	ExtractDataToCoeffs (const NekDouble data, const std::vector< unsigned int > &nummodes, const int nmodes_offset, NekDouble coeffs)

NekDouble	StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)

int	GetCoordim ()

void	GetBoundaryMap (Array< OneD, unsigned int > &outarray)

void	GetInteriorMap (Array< OneD, unsigned int > &outarray)

int	GetVertexMap (const int localVertexId, bool useCoeffPacking=false)

void	GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)

void	GetFaceInteriorMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)

void	GetEdgeToElementMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int P=-1)

void	GetFaceToElementMap (const int fid, const Orientation faceOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int nummodesA=-1, int nummodesB=-1)

void	GetEdgePhysVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Extract the physical values along edge edge from inarray into outarray following the local edge orientation and point distribution defined by defined in EdgeExp. More...

void	GetEdgePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GetTracePhysVals (const int edge, const boost::shared_ptr< StdExpansion > &EdgeExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GetVertexPhysVals (const int vertex, const Array< OneD, const NekDouble > &inarray, NekDouble &outarray)

void	GetEdgeInterpVals (const int edge, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GetEdgeQFactors (const int edge, Array< OneD, NekDouble > &outarray)
	Extract the metric factors to compute the contravariant fluxes along edge edge and stores them into outarray following the local edge orientation (i.e. anticlockwise convention). More...

void	GetFacePhysVals (const int face, const boost::shared_ptr< StdExpansion > &FaceExp, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, StdRegions::Orientation orient=eNoOrientation)

void	GetEdgePhysMap (const int edge, Array< OneD, int > &outarray)

void	GetFacePhysMap (const int face, Array< OneD, int > &outarray)

void	MultiplyByQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

DNekMatSharedPtr	CreateGeneralMatrix (const StdMatrixKey &mkey)
	this function generates the mass matrix $\mathbf{M}[i][j] = \int \phi_i(\mathbf{x}) \phi_j(\mathbf{x}) d\mathbf{x}$ More...

void	GeneralMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdMatrixKey &mkey)

void	LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDerivMatrixOp (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDirectionalDerivMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassLevelCurvatureMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LinearAdvectionDiffusionReactionMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)

void	HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

DNekMatSharedPtr	GenMatrix (const StdMatrixKey &mkey)

void	PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)

void	PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	PhysDeriv_s (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_ds)

void	PhysDeriv_n (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_dn)

void	PhysDirectionalDeriv (const Array< OneD, const NekDouble > &inarray, const Array< OneD, const NekDouble > &direction, Array< OneD, NekDouble > &outarray)

void	StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1=NullNekDouble1DArray, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)

void	StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	AddRobinMassMatrix (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, DNekMatSharedPtr &inoutmat)

void	AddRobinEdgeContribution (const int edgeid, const Array< OneD, const NekDouble > &primCoeffs, Array< OneD, NekDouble > &coeffs)

NekDouble	PhysEvaluate (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
	This function evaluates the expansion at a single (arbitrary) point of the domain. More...

NekDouble	PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)
	This function evaluates the expansion at a single (arbitrary) point of the domain. More...

void	LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)
	Convert local cartesian coordinate xi into local collapsed coordinates eta. More...

const boost::shared_ptr < SpatialDomains::GeomFactors > &	GetMetricInfo (void) const

virtual int	v_GetElmtId ()
	Get the element id of this expansion when used in a list by returning value of m_elmt_id. More...

virtual const Array< OneD, const NekDouble > &	v_GetPhysNormals (void)

virtual void	v_SetPhysNormals (Array< OneD, const NekDouble > &normal)

virtual void	v_SetUpPhysNormals (const int edge)

virtual void	v_ExtractDataToCoeffs (const NekDouble data, const std::vector< unsigned int > &nummodes, const int nmode_offset, NekDouble coeffs)
	Unpack data from input file assuming it comes from the same expansion type. More...

virtual void	v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, Array< OneD, NekDouble > &outarray)

virtual void	v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, Array< OneD, NekDouble > &outarray)

virtual void	v_NormVectorIProductWRTBase (const Array< OneD, const NekDouble > &Fx, const Array< OneD, const NekDouble > &Fy, const Array< OneD, const NekDouble > &Fz, Array< OneD, NekDouble > &outarray)

virtual void	v_NormVectorIProductWRTBase (const Array< OneD, const Array< OneD, NekDouble > > &Fvec, Array< OneD, NekDouble > &outarray)

virtual DNekScalBlkMatSharedPtr	v_GetLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)

virtual void	v_DropLocStaticCondMatrix (const LocalRegions::MatrixKey &mkey)

virtual StdRegions::Orientation	v_GetForient (int face)

virtual StdRegions::Orientation	v_GetEorient (int edge)

virtual StdRegions::Orientation	v_GetCartesianEorient (int edge)

virtual StdRegions::Orientation	v_GetPorient (int point)

NekDouble	Linf (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
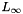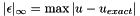	Function to evaluate the discrete $L_\infty$ error $\|\epsilon\|_\infty = \max \|u - u_{exact}\|$ where $u_{exact}$ is given by the array sol. More...

NekDouble	L2 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
	Function to evaluate the discrete 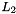error, $\| \epsilon \|_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 dx \right]^{1/2} d\xi_1$ where $u_{exact}$ is given by the array sol. More...

NekDouble	H1 (const Array< OneD, const NekDouble > &phys, const Array< OneD, const NekDouble > &sol=NullNekDouble1DArray)
	Function to evaluate the discrete 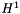error, $\| \epsilon \|^1_{2} = \left [ \int^1_{-1} [u - u_{exact}]^2 + \nabla(u - u_{exact})\cdot\nabla(u - u_{exact})\cdot dx \right]^{1/2} d\xi_1$ where $u_{exact}$ is given by the array sol. More...

const NormalVector &	GetEdgeNormal (const int edge) const

void	ComputeEdgeNormal (const int edge)

void	NegateEdgeNormal (const int edge)

bool	EdgeNormalNegated (const int edge)

void	ComputeFaceNormal (const int face)

void	NegateFaceNormal (const int face)

bool	FaceNormalNegated (const int face)

void	ComputeVertexNormal (const int vertex)

const NormalVector &	GetFaceNormal (const int face) const

const NormalVector &	GetVertexNormal (const int vertex) const

const NormalVector &	GetSurfaceNormal (const int id) const

const LibUtilities::PointsKeyVector	GetPointsKeys () const

Array< OneD, unsigned int >	GetEdgeInverseBoundaryMap (int eid)

Array< OneD, unsigned int >	GetFaceInverseBoundaryMap (int fid, StdRegions::Orientation faceOrient=eNoOrientation)

DNekMatSharedPtr	BuildInverseTransformationMatrix (const DNekScalMatSharedPtr &m_transformationmatrix)

void	PhysInterpToSimplexEquiSpaced (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, int npset=-1)
	This function performs an interpolation from the physical space points provided at input into an array of equispaced points which are not the collapsed coordinate. So for a tetrahedron you will only get a tetrahedral number of values. More...

void	GetSimplexEquiSpacedConnectivity (Array< OneD, int > &conn, bool standard=true)
	This function provides the connectivity of local simplices (triangles or tets) to connect the equispaced data points provided by PhysInterpToSimplexEquiSpaced. More...

void	EquiSpacedToCoeffs (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	This function performs a projection/interpolation from the equispaced points sometimes used in post-processing onto the coefficient space. More...

template<class T >
boost::shared_ptr< T >	as ()

void	IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)

Protected Member Functions
virtual NekDouble	v_Integral (const Array< OneD, const NekDouble > &inarray)
	Integrates the specified function over the domain. More...

virtual void	v_PhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)
	Calculate the derivative of the physical points. More...

virtual void	v_PhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Calculate the derivative of the physical points in a given direction. More...

virtual void	v_StdPhysDeriv (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &out_d0, Array< OneD, NekDouble > &out_d1, Array< OneD, NekDouble > &out_d2=NullNekDouble1DArray)

virtual void	v_StdPhysDeriv (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_BwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Backward tranform for triangular elements. More...

virtual void	v_BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_BwdTrans_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1)

virtual void	v_FwdTrans (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Transform a given function from physical quadrature space to coefficient space. More...

virtual void	v_FwdTrans_BndConstrained (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_IProductWRTBase (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)
	Calculate the inner product of inarray with respect to the basis B=base0[p]*base1[pq] and put into outarray. More...

virtual void	v_IProductWRTBase_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_IProductWRTBase_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, bool multiplybyweights=true)

virtual void	v_IProductWRTBase_SumFacKernel (const Array< OneD, const NekDouble > &base0, const Array< OneD, const NekDouble > &base1, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp, bool doCheckCollDir0, bool doCheckCollDir1)

virtual void	v_IProductWRTDerivBase (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_IProductWRTDerivBase_MatOp (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_LocCoordToLocCollapsed (const Array< OneD, const NekDouble > &xi, Array< OneD, NekDouble > &eta)

virtual void	v_FillMode (const int mode, Array< OneD, NekDouble > &outarray)

virtual int	v_GetNverts () const

virtual int	v_GetNedges () const

virtual LibUtilities::ShapeType	v_DetShapeType () const

virtual int	v_NumBndryCoeffs () const

virtual int	v_NumDGBndryCoeffs () const

virtual int	v_GetEdgeNcoeffs (const int i) const

virtual int	v_GetEdgeNumPoints (const int i) const

virtual int	v_CalcNumberOfCoefficients (const std::vector< unsigned int > &nummodes, int &modes_offset)

virtual LibUtilities::BasisType	v_GetEdgeBasisType (const int i) const

virtual void	v_GetCoords (Array< OneD, NekDouble > &coords_x, Array< OneD, NekDouble > &coords_y, Array< OneD, NekDouble > &coords_z)

virtual bool	v_IsBoundaryInteriorExpansion ()

virtual int	v_DetCartesianDirOfEdge (const int edge)

virtual const LibUtilities::BasisKey	v_DetEdgeBasisKey (const int edge) const

virtual void	v_GetEdgeToElementMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray, int P=-1)

virtual int	v_GetVertexMap (int localVertexId, bool useCoeffPacking=false)

virtual void	v_GetEdgeInteriorMap (const int eid, const Orientation edgeOrient, Array< OneD, unsigned int > &maparray, Array< OneD, int > &signarray)

virtual void	v_GetInteriorMap (Array< OneD, unsigned int > &outarray)

virtual void	v_GetBoundaryMap (Array< OneD, unsigned int > &outarray)

virtual DNekMatSharedPtr	v_GenMatrix (const StdMatrixKey &mkey)

virtual DNekMatSharedPtr	v_CreateStdMatrix (const StdMatrixKey &mkey)

virtual void	v_MassMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_LaplacianMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_SVVLaplacianFilter (Array< OneD, NekDouble > &array, const StdMatrixKey &mkey)

virtual void	v_ReduceOrderCoeffs (int numMin, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_LaplacianMatrixOp (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_WeakDerivMatrixOp (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_HelmholtzMatrixOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_GeneralMatrixOp_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_MultiplyByStdQuadratureMetric (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_GetSimplexEquiSpacedConnectivity (Array< OneD, int > &conn, bool standard=true)

Protected Member Functions inherited from Nektar::StdRegions::StdExpansion2D
virtual NekDouble	v_PhysEvaluate (const Array< OneD, const NekDouble > &coords, const Array< OneD, const NekDouble > &physvals)
	This function evaluates the expansion at a single (arbitrary) point of the domain. More...

virtual NekDouble	v_PhysEvaluate (const Array< OneD, DNekMatSharedPtr > &I, const Array< OneD, const NekDouble > &physvals)

virtual void	v_LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual void	v_HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdRegions::StdMatrixKey &mkey)

virtual int	v_GetTraceNcoeffs (const int i) const

Protected Member Functions inherited from Nektar::StdRegions::StdExpansion
DNekMatSharedPtr	CreateStdMatrix (const StdMatrixKey &mkey)

DNekBlkMatSharedPtr	CreateStdStaticCondMatrix (const StdMatrixKey &mkey)
	Create the static condensation of a matrix when using a boundary interior decomposition. More...

IndexMapValuesSharedPtr	CreateIndexMap (const IndexMapKey &ikey)
	Create an IndexMap which contains mapping information linking any specific element shape with either its boundaries, edges, faces, verteces, etc. More...

void	BwdTrans_MatOp (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	BwdTrans_SumFac (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	IProductWRTDerivBase_SumFac (const int dir, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

void	GeneralMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp_MatFree_Kernel (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wsp)

void	LaplacianMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LaplacianMatrixOp_MatFree (const int k1, const int k2, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDerivMatrixOp_MatFree (const int i, const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	WeakDirectionalDerivMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	MassLevelCurvatureMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	LinearAdvectionDiffusionReactionMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey, bool addDiffusionTerm=true)

void	HelmholtzMatrixOp_MatFree (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

void	HelmholtzMatrixOp_MatFree_GenericImpl (const Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray, const StdMatrixKey &mkey)

virtual void	v_SetCoeffsToOrientation (StdRegions::Orientation dir, Array< OneD, const NekDouble > &inarray, Array< OneD, NekDouble > &outarray)

virtual void	v_SetCoeffsToOrientation (Array< OneD, NekDouble > &coeffs, StdRegions::Orientation dir)

virtual NekDouble	v_StdPhysEvaluate (const Array< OneD, const NekDouble > &Lcoord, const Array< OneD, const NekDouble > &physvals)

Additional Inherited Members
Protected Attributes inherited from Nektar::StdRegions::StdExpansion
Array< OneD, LibUtilities::BasisSharedPtr >	m_base

int	m_elmt_id

int	m_ncoeffs

LibUtilities::NekManager < StdMatrixKey, DNekMat, StdMatrixKey::opLess >	m_stdMatrixManager

LibUtilities::NekManager < StdMatrixKey, DNekBlkMat, StdMatrixKey::opLess >	m_stdStaticCondMatrixManager

LibUtilities::NekManager < IndexMapKey, IndexMapValues, IndexMapKey::opLess >	m_IndexMapManager

Detailed Description

Definition at line 50 of file StdTriExp.h.

Constructor & Destructor Documentation

Nektar::StdRegions::StdTriExp::StdTriExp ( )

Definition at line 47 of file StdTriExp.cpp.

48 {

49 }

Nektar::StdRegions::StdTriExp::StdTriExp	(	const LibUtilities::BasisKey &	Ba,
		const LibUtilities::BasisKey &	Bb
	)

Definition at line 52 of file StdTriExp.cpp.

References ASSERTL0, and Nektar::LibUtilities::BasisKey::GetNumModes().

                                             :
             StdExpansion (LibUtilities::StdTriData::getNumberOfCoefficients(
                               Ba.GetNumModes(),
                               Bb.GetNumModes()),
                           2,Ba,Bb),
             StdExpansion2D(LibUtilities::StdTriData::getNumberOfCoefficients(
                                Ba.GetNumModes(),
                                Bb.GetNumModes()),
                            Ba,Bb)
         {
             ASSERTL0(Ba.GetNumModes() <= Bb.GetNumModes(),
                      "order in 'a' direction is higher than order "
                      "in 'b' direction");
         }

Nektar::StdRegions::StdTriExp::StdTriExp ( const StdTriExp & T )

Definition at line 69 of file StdTriExp.cpp.

                                               :
             StdExpansion(T),
             StdExpansion2D(T)
         {
         }

Nektar::StdRegions::StdTriExp::~StdTriExp ( )

Definition at line 75 of file StdTriExp.cpp.

76 {

77 }

Member Function Documentation

void Nektar::StdRegions::StdTriExp::v_BwdTrans	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Backward tranform for triangular elements.

Note: 'q' (base[1]) runs fastest in this element.

Implements Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 252 of file StdTriExp.cpp.

References v_BwdTrans_SumFac().

         {
             v_BwdTrans_SumFac(inarray,outarray);
         }

void Nektar::StdRegions::StdTriExp::v_BwdTrans_SumFac	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 260 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion2D::BwdTrans_SumFacKernel(), Nektar::StdRegions::StdExpansion::GetNumPoints(), and Nektar::StdRegions::StdExpansion::m_base.

Referenced by v_BwdTrans(), and Nektar::StdRegions::StdNodalTriExp::v_BwdTrans_SumFac().

         {
             Array<OneD, NekDouble> wsp(m_base[0]->GetNumPoints()*
                                        m_base[1]->GetNumModes());
 
             BwdTrans_SumFacKernel(m_base[0]->GetBdata(),
                                   m_base[1]->GetBdata(),
                                   inarray,outarray,wsp);
         }

void Nektar::StdRegions::StdTriExp::v_BwdTrans_SumFacKernel	(	const Array< OneD, const NekDouble > &	base0,
		const Array< OneD, const NekDouble > &	base1,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		Array< OneD, NekDouble > &	wsp,
		bool	doCheckCollDir0,
		bool	doCheckCollDir1
	)

protectedvirtual

Implements Nektar::StdRegions::StdExpansion2D.

Definition at line 272 of file StdTriExp.cpp.

References ASSERTL1, ASSERTL2, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::LibUtilities::eOrtho_B, Nektar::StdRegions::StdExpansion::GetBasisType(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             int  i;
             int  mode;
             int  nquad0  = m_base[0]->GetNumPoints();
             int  nquad1  = m_base[1]->GetNumPoints();
             int  nmodes0 = m_base[0]->GetNumModes();
             int  nmodes1 = m_base[1]->GetNumModes();
 
             ASSERTL1(wsp.num_elements() >= nquad0*nmodes1,
                      "Workspace size is not sufficient");
             ASSERTL2((m_base[1]->GetBasisType() != LibUtilities::eOrtho_B)||
                      (m_base[1]->GetBasisType() != LibUtilities::eModified_B),
                      "Basis[1] is not of general tensor type");
 
             for (i = mode = 0; i < nmodes0; ++i)
             {
                 Blas::Dgemv('N', nquad1,nmodes1-i,1.0,base1.get()+mode*nquad1,
                             nquad1,&inarray[0]+mode,1,0.0,&wsp[0]+i*nquad1,1);
                 mode += nmodes1-i;
             }
 
             // fix for modified basis by splitting top vertex mode
             if(m_base[0]->GetBasisType() == LibUtilities::eModified_A)
             {
                 Blas::Daxpy(nquad1,inarray[1],base1.get()+nquad1,1,
                             &wsp[0]+nquad1,1);
             }
 
             Blas::Dgemm('N','T', nquad0,nquad1,nmodes0,1.0, base0.get(),nquad0,
                         &wsp[0], nquad1,0.0, &outarray[0], nquad0);
         }

int Nektar::StdRegions::StdTriExp::v_CalcNumberOfCoefficients	(	const std::vector< unsigned int > &	nummodes,
		int &	modes_offset
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 804 of file StdTriExp.cpp.

References Nektar::LibUtilities::StdTriData::getNumberOfCoefficients().

         {
             int nmodes = LibUtilities::StdTriData::getNumberOfCoefficients(
                 nummodes[modes_offset],
                 nummodes[modes_offset+1]);
             modes_offset += 2;
 
             return nmodes;
         }

DNekMatSharedPtr Nektar::StdRegions::StdTriExp::v_CreateStdMatrix ( const StdMatrixKey & mkey )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 1335 of file StdTriExp.cpp.

References v_GenMatrix().

         {
             return v_GenMatrix(mkey);
         }

int Nektar::StdRegions::StdTriExp::v_DetCartesianDirOfEdge ( const int edge )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 857 of file StdTriExp.cpp.

References ASSERTL2.

         {
             ASSERTL2(edge >= 0 && edge <= 2, "edge id is out of range");
 
             return edge == 0 ? 0 : 1;
         }

const LibUtilities::BasisKey Nektar::StdRegions::StdTriExp::v_DetEdgeBasisKey ( const int edge ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 864 of file StdTriExp.cpp.

References ASSERTL0, ASSERTL2, Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::eGaussRadauMAlpha1Beta0, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetBasis(), Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::StdRegions::StdExpansion::GetNumPoints(), Nektar::StdRegions::StdExpansion::GetPointsType(), Nektar::StdRegions::StdExpansion::m_base, and Nektar::LibUtilities::NullBasisKey().

         {
             ASSERTL2(i >= 0 && i <= 2, "edge id is out of range");
 
             if (i == 0)
             {
                 return GetBasis(0)->GetBasisKey();
             }
             else
             {
                 switch(m_base[1]->GetBasisType())
                 {
                 case LibUtilities::eModified_B:
                 {
                     switch(m_base[1]->GetPointsType())
                     {
                     case LibUtilities::eGaussRadauMAlpha1Beta0:
                     {
                         LibUtilities::PointsKey pkey(
                                 m_base[1]->GetBasisKey().GetPointsKey().
                                 GetNumPoints()+1,
                                 LibUtilities::eGaussLobattoLegendre);
                         return LibUtilities::BasisKey(
                                 LibUtilities::eModified_A,
                                 m_base[1]->GetNumModes(),pkey);
                         break;
                     }
 
                     default:
                         ASSERTL0(false,"unexpected points distribution");
                         break;
                     }
                 }
                 default:
                     ASSERTL0(false,"Information not available to set edge key");
                     break;
                 }
             }
             return LibUtilities::NullBasisKey;
         }

LibUtilities::ShapeType Nektar::StdRegions::StdTriExp::v_DetShapeType ( ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 751 of file StdTriExp.cpp.

References Nektar::LibUtilities::eTriangle.

         {
             return LibUtilities::eTriangle;
         }

void Nektar::StdRegions::StdTriExp::v_FillMode	(	const int	mode,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 692 of file StdTriExp.cpp.

References ASSERTL2, Nektar::LibUtilities::eModified_A, Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion::m_ncoeffs, Vmath::Vcopy(), and Vmath::Vmul().

Referenced by Nektar::StdRegions::StdNodalTriExp::GenNBasisTransMatrix().

         {
             int   i,m;
             int   nquad0 = m_base[0]->GetNumPoints();
             int   nquad1 = m_base[1]->GetNumPoints();
             int   order0 = m_base[0]->GetNumModes();
             int   order1 = m_base[1]->GetNumModes();
             int   mode0  = 0;
             Array<OneD, const NekDouble> base0 = m_base[0]->GetBdata();
             Array<OneD, const NekDouble> base1 = m_base[1]->GetBdata();
 
             ASSERTL2(mode <= m_ncoeffs,
                      "calling argument mode is larger than "
                      "total expansion order");
 
             m = order1;
             for (i = 0; i < order0; ++i, m+=order1-i)
             {
                 if (m > mode)
                 {
                     mode0 = i;
                     break;
                 }
             }
 
             // deal with top vertex mode in modified basis
             if (mode == 1 &&
                 m_base[0]->GetBasisType() == LibUtilities::eModified_A)
             {
                 Vmath::Fill(nquad0*nquad1 , 1.0, outarray, 1);
             }
             else
             {
                 for (i = 0; i < nquad1; ++i)
                 {
                     Vmath::Vcopy(nquad0,(NekDouble *)(base0.get()+mode0*nquad0),
                                  1,&outarray[0]+i*nquad0,1);
                 }
             }
 
             for(i = 0; i < nquad0; ++i)
             {
                 Vmath::Vmul(nquad1,(NekDouble *)(base1.get() + mode*nquad1),
                             1,&outarray[0]+i,nquad0,&outarray[0]+i,nquad0);
             }
         }

void Nektar::StdRegions::StdTriExp::v_FwdTrans	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Transform a given function from physical quadrature space to coefficient space.

See also: StdExpansion::FwdTrans

Implements Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 312 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::eCopy, Nektar::StdRegions::eInvMass, Nektar::eWrapper, Nektar::StdRegions::StdExpansion::GetStdMatrix(), Nektar::StdRegions::StdExpansion::m_ncoeffs, and v_IProductWRTBase().

         {
             v_IProductWRTBase(inarray,outarray);
 
             // get Mass matrix inverse
             StdMatrixKey      masskey(eInvMass,DetShapeType(),*this);
             DNekMatSharedPtr  matsys = GetStdMatrix(masskey);
 
             // copy inarray in case inarray == outarray
             NekVector<NekDouble> in(m_ncoeffs,outarray,eCopy);
             NekVector<NekDouble> out(m_ncoeffs,outarray,eWrapper);
 
             out = (*matsys)*in;
         }

void Nektar::StdRegions::StdTriExp::v_FwdTrans_BndConstrained	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::TriExp.

Definition at line 330 of file StdTriExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eForwards, Nektar::StdRegions::eMass, Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion::m_ncoeffs, Nektar::StdRegions::StdExpansion::m_stdStaticCondMatrixManager, Nektar::StdRegions::StdExpansion::MassMatrixOp(), sign, v_GetEdgeToElementMap(), v_GetInteriorMap(), v_IProductWRTBase(), v_NumBndryCoeffs(), and Vmath::Vsub().

         {
             int i,j;
             int npoints[2] = {m_base[0]->GetNumPoints(),
                               m_base[1]->GetNumPoints()};
             int nmodes[2]  = {m_base[0]->GetNumModes(),
                               m_base[1]->GetNumModes()};
 
             fill(outarray.get(), outarray.get()+m_ncoeffs, 0.0 );
 
             Array<OneD, NekDouble> physEdge[3];
             Array<OneD, NekDouble> coeffEdge[3];
             for(i = 0; i < 3; i++)
             {
                 physEdge[i]  = Array<OneD, NekDouble>(npoints[i!=0]);
                 coeffEdge[i] = Array<OneD, NekDouble>(nmodes[i!=0]);
             }
 
             for(i = 0; i < npoints[0]; i++)
             {
                 physEdge[0][i] = inarray[i];
             }
 
             for(i = 0; i < npoints[1]; i++)
             {
                 physEdge[1][i] = inarray[npoints[0]-1+i*npoints[0]];
                 physEdge[2][i] = inarray[(npoints[1]-1)*npoints[0]-i*npoints[0]];
             }
 
             StdSegExpSharedPtr segexp[2] = {
                 MemoryManager<StdRegions::StdSegExp>::AllocateSharedPtr(
                     m_base[0]->GetBasisKey()),
                 MemoryManager<StdRegions::StdSegExp>::AllocateSharedPtr(
                     m_base[1]->GetBasisKey())
             };
 
             Array<OneD, unsigned int> mapArray;
             Array<OneD, int>          signArray;
             NekDouble sign;
 
             for (i = 0; i < 3; i++)
             {
                 //segexp[i!=0]->v_FwdTrans_BndConstrained(physEdge[i],coeffEdge[i]);
                 segexp[i!=0]->FwdTrans_BndConstrained(physEdge[i],coeffEdge[i]);
 
                 v_GetEdgeToElementMap(i,eForwards,mapArray,signArray);
                 for (j = 0; j < nmodes[i != 0]; j++)
                 {
                     sign = (NekDouble) signArray[j];
                     outarray[ mapArray[j] ] = sign * coeffEdge[i][j];
                 }
             }
 
             Array<OneD, NekDouble> tmp0(m_ncoeffs);
             Array<OneD, NekDouble> tmp1(m_ncoeffs);
 
             StdMatrixKey      masskey(eMass,DetShapeType(),*this);
             MassMatrixOp(outarray,tmp0,masskey);
             v_IProductWRTBase(inarray,tmp1);
 
             Vmath::Vsub(m_ncoeffs, tmp1, 1, tmp0, 1, tmp1, 1);
 
             // get Mass matrix inverse (only of interior DOF)
             // use block (1,1) of the static condensed system
             // note: this block alreay contains the inverse matrix
             DNekMatSharedPtr matsys =
                 (m_stdStaticCondMatrixManager[masskey])->GetBlock(1,1);
 
             int nBoundaryDofs = v_NumBndryCoeffs();
             int nInteriorDofs = m_ncoeffs - nBoundaryDofs;
 
             Array<OneD, NekDouble> rhs   (nInteriorDofs);
             Array<OneD, NekDouble> result(nInteriorDofs);
 
             v_GetInteriorMap(mapArray);
 
             for (i = 0; i < nInteriorDofs; i++)
             {
                 rhs[i] = tmp1[ mapArray[i] ];
             }
 
             Blas::Dgemv('N',nInteriorDofs,nInteriorDofs,
                         1.0,&(matsys->GetPtr())[0],nInteriorDofs,
                         rhs.get(),1,
                         0.0,result.get(),1);
 
             for (i = 0; i < nInteriorDofs; i++)
             {
                 outarray[ mapArray[i] ] = result[i];
             }
         }

void Nektar::StdRegions::StdTriExp::v_GeneralMatrixOp_MatOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented in Nektar::LocalRegions::TriExp.

Definition at line 1539 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::m_ncoeffs, Nektar::StdRegions::StdExpansion::m_stdMatrixManager, and Vmath::Vcopy().

         {
             DNekMatSharedPtr mat = m_stdMatrixManager[mkey];
 
             if(inarray.get() == outarray.get())
             {
                 Array<OneD,NekDouble> tmp(m_ncoeffs);
                 Vmath::Vcopy(m_ncoeffs,inarray.get(),1,tmp.get(),1);
 
                 Blas::Dgemv('N', m_ncoeffs, m_ncoeffs, 1.0, mat->GetPtr().get(),
                             m_ncoeffs, tmp.get(), 1, 0.0, outarray.get(), 1);
             }
             else
             {
                 Blas::Dgemv('N', m_ncoeffs, m_ncoeffs, 1.0, mat->GetPtr().get(),
                             m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
             }
         }

DNekMatSharedPtr Nektar::StdRegions::StdTriExp::v_GenMatrix ( const StdMatrixKey & mkey )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::TriExp, Nektar::StdRegions::StdNodalTriExp, and Nektar::LocalRegions::NodalTriExp.

Definition at line 1258 of file StdTriExp.cpp.

Referenced by v_CreateStdMatrix().

         {
 
             MatrixType mtype   = mkey.GetMatrixType();
 
             DNekMatSharedPtr Mat;
 
             switch(mtype)
             {
                 case ePhysInterpToEquiSpaced:
                 {
                     int nq0, nq1, nq;
 
                     nq0 = m_base[0]->GetNumPoints();
                     nq1 = m_base[1]->GetNumPoints();
 
                     // take definition from key
                     if(mkey.ConstFactorExists(eFactorConst))
                     {
                         nq = (int) mkey.GetConstFactor(eFactorConst);
                     }
                     else
                     {
                         nq = max(nq0,nq1);
                     }
 
                     int neq = LibUtilities::StdTriData::
                                                 getNumberOfCoefficients(nq,nq);
                     Array<OneD, Array<OneD, NekDouble> > coords(neq);
                     Array<OneD, NekDouble>               coll  (2);
                     Array<OneD, DNekMatSharedPtr>        I     (2);
                     Array<OneD, NekDouble>               tmp   (nq0);
 
 
                     Mat = MemoryManager<DNekMat>::AllocateSharedPtr(neq,nq0*nq1);
                     int cnt = 0;
 
                     for(int i = 0; i < nq; ++i)
                     {
                         for(int j = 0; j < nq-i; ++j,++cnt)
                         {
                             coords[cnt]    = Array<OneD, NekDouble>(2);
                             coords[cnt][0] = -1.0 + 2*j/(NekDouble)(nq-1);
                             coords[cnt][1] = -1.0 + 2*i/(NekDouble)(nq-1);
                         }
                     }
 
                     for(int i = 0; i < neq; ++i)
                     {
                         LocCoordToLocCollapsed(coords[i],coll);
 
                         I[0] = m_base[0]->GetI(coll);
                         I[1] = m_base[1]->GetI(coll+1);
 
                         // interpolate first coordinate direction
                         for (int j  = 0; j < nq1; ++j)
                         {
                             NekDouble fac = (I[1]->GetPtr())[j];
                             Vmath::Smul(nq0, fac, I[0]->GetPtr(), 1, tmp, 1);
 
                             Vmath::Vcopy(nq0, &tmp[0], 1,
                                          Mat->GetRawPtr() + j*nq0*neq + i, neq);
                         }
 
                     }
                     break;
                 }
                 default:
                 {
                     Mat = StdExpansion::CreateGeneralMatrix(mkey);
                     break;
                 }
             }
 
             return Mat;
         }

void Nektar::StdRegions::StdTriExp::v_GetBoundaryMap ( Array< OneD, unsigned int > & outarray )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 1221 of file StdTriExp.cpp.

References ASSERTL1, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::StdRegions::StdExpansion::m_base, and Nektar::StdRegions::StdExpansion::NumBndryCoeffs().

         {
             ASSERTL1(GetBasisType(0) == LibUtilities::eModified_A &&
                      GetBasisType(1) == LibUtilities::eModified_B,
                      "Expansion not of expected type");
             int i;
             int cnt;
             int nummodes0, nummodes1;
             int value;
 
             if (outarray.num_elements()!=NumBndryCoeffs())
             {
                 outarray = Array<OneD, unsigned int>(NumBndryCoeffs());
             }
 
             nummodes0 = m_base[0]->GetNumModes();
             nummodes1 = m_base[1]->GetNumModes();
 
             value = 2*nummodes1-1;
             for(i = 0; i < value; i++)
             {
                 outarray[i]=i;
             }
             cnt = value;
 
             for(i = 0; i < nummodes0-2; i++)
             {
                 outarray[cnt++]=value;
                 value += nummodes1-2-i;
             }
         }

void Nektar::StdRegions::StdTriExp::v_GetCoords	(	Array< OneD, NekDouble > &	coords_x,
		Array< OneD, NekDouble > &	coords_y,
		Array< OneD, NekDouble > &	coords_z
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, and Nektar::LocalRegions::TriExp.

Definition at line 831 of file StdTriExp.cpp.

References Vmath::Fill(), Nektar::StdRegions::StdExpansion::GetNumPoints(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             Array<OneD, const NekDouble> z0 = m_base[0]->GetZ();
             Array<OneD, const NekDouble> z1 = m_base[1]->GetZ();
             int nq0 = GetNumPoints(0);
             int nq1 = GetNumPoints(1);
             int i,j;
 
             for(i = 0; i < nq1; ++i)
             {
                 for(j = 0; j < nq0; ++j)
                 {
                     coords_0[i*nq0+j] = (1+z0[j])*(1-z1[i])/2.0 - 1.0;
                 }
                 Vmath::Fill(nq0,z1[i],&coords_1[0] + i*nq0,1);
             }
         }

LibUtilities::BasisType Nektar::StdRegions::StdTriExp::v_GetEdgeBasisType ( const int i ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 816 of file StdTriExp.cpp.

References ASSERTL2, and Nektar::StdRegions::StdExpansion::GetBasisType().

         {
             ASSERTL2(i >= 0 && i <= 2, "edge id is out of range");
 
             if (i == 0)
             {
                 return GetBasisType(0);
             }
             else
             {
                 return GetBasisType(1);
             }
         }

void Nektar::StdRegions::StdTriExp::v_GetEdgeInteriorMap	(	const int	eid,
		const Orientation	edgeOrient,
		Array< OneD, unsigned int > &	maparray,
		Array< OneD, int > &	signarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 1105 of file StdTriExp.cpp.

References ASSERTL0, Nektar::StdRegions::eBackwards, Nektar::StdRegions::eForwards, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetEdgeBasisType(), Nektar::StdRegions::StdExpansion::GetEdgeNcoeffs(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             ASSERTL0(GetEdgeBasisType(eid) == LibUtilities::eModified_A||
                      GetEdgeBasisType(eid) == LibUtilities::eModified_B,
                      "Mapping not defined for this type of basis");
             int i;
             const int nummodes1 = m_base[1]->GetNumModes();
             const int nEdgeIntCoeffs = GetEdgeNcoeffs(eid)-2;
 
             if(maparray.num_elements() != nEdgeIntCoeffs)
             {
                 maparray = Array<OneD, unsigned int>(nEdgeIntCoeffs);
             }
 
             if(signarray.num_elements() != nEdgeIntCoeffs)
             {
                 signarray = Array<OneD, int>(nEdgeIntCoeffs,1);
             }
             else
             {
                 fill( signarray.get() , signarray.get()+nEdgeIntCoeffs, 1 );
             }
 
             switch(eid)
             {
                 case 0:
                 {
                     int cnt = 2*nummodes1 - 1;
                     for(i = 0; i < nEdgeIntCoeffs; cnt+=nummodes1-2-i, ++i)
                     {
                         maparray[i] = cnt;
                     }
 
                     if(edgeOrient==eBackwards)
                     {
                         for(i = 1; i < nEdgeIntCoeffs; i+=2)
                         {
                             signarray[i] = -1;
                         }
                     }
                     break;
                 }
                 case 1:
                 {
                     for(i = 0; i < nEdgeIntCoeffs; i++)
                     {
                         maparray[i] = nummodes1+1+i;
                     }
 
                     if(edgeOrient==eBackwards)
                     {
                         for(i = 1; i < nEdgeIntCoeffs; i+=2)
                         {
                             signarray[i] = -1;
                         }
                     }
                     break;
                 }
                 case 2:
                 {
                     for(i = 0; i < nEdgeIntCoeffs; i++)
                     {
                         maparray[i] = 2+i;
                     }
 
                     if(edgeOrient==eForwards)
                     {
                         for(i = 1; i < nEdgeIntCoeffs; i+=2)
                         {
                             signarray[i] = -1;
                         }
                     }
                     break;
                 }
                 default:
                 {
                     ASSERTL0(false,"eid must be between 0 and 2");
                     break;
                 }
             }
         }

int Nektar::StdRegions::StdTriExp::v_GetEdgeNcoeffs ( const int i ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 776 of file StdTriExp.cpp.

References ASSERTL2, and Nektar::StdRegions::StdExpansion::GetBasisNumModes().

         {
             ASSERTL2(i >= 0 && i <= 2, "edge id is out of range");
 
             if (i == 0)
             {
                 return GetBasisNumModes(0);
             }
             else
             {
                 return GetBasisNumModes(1);
             }
         }

int Nektar::StdRegions::StdTriExp::v_GetEdgeNumPoints ( const int i ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 790 of file StdTriExp.cpp.

References ASSERTL2, and Nektar::StdRegions::StdExpansion::GetNumPoints().

         {
             ASSERTL2((i >= 0)&&(i <= 2),"edge id is out of range");
 
             if (i == 0)
             {
                 return GetNumPoints(0);
             }
             else
             {
                 return GetNumPoints(1);
             }
         }

void Nektar::StdRegions::StdTriExp::v_GetEdgeToElementMap	(	const int	eid,
		const Orientation	edgeOrient,
		Array< OneD, unsigned int > &	maparray,
		Array< OneD, int > &	signarray,
		int	P = `-1`
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 912 of file StdTriExp.cpp.

References ASSERTL0, ASSERTL1, Nektar::StdRegions::eBackwards, Nektar::StdRegions::eForwards, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetEdgeBasisType(), and Nektar::StdRegions::StdExpansion::m_base.

Referenced by v_FwdTrans_BndConstrained().

         {
             ASSERTL1(GetEdgeBasisType(eid) == LibUtilities::eModified_A ||
                      GetEdgeBasisType(eid) == LibUtilities::eModified_B,
                      "Mapping not defined for this type of basis");
 
             int i;
             int numModes;
             int order0 = m_base[0]->GetNumModes();
             int order1 = m_base[1]->GetNumModes();
 
             switch (eid)
             {
             case 0:
                 numModes = order0;
                 break;
             case 1:
             case 2:
                 numModes = order1;
                 break;
             }
 
             bool checkForZeroedModes = false;
             if (P == -1)
             {
                 P = numModes;
             }
             else if(P != numModes)
             {
                 checkForZeroedModes = true;
             }
 
 
             if(maparray.num_elements() != P)
             {
                 maparray = Array<OneD, unsigned int>(P);
             }
 
             if(signarray.num_elements() != P)
             {
                 signarray = Array<OneD, int>(P,1);
             }
             else
             {
                 fill(signarray.get() , signarray.get()+P, 1);
             }
 
             switch(eid)
             {
                 case 0:
                 {
                     int cnt = 0;
                     for(i = 0; i < P; cnt+=order1-i, ++i)
                     {
                         maparray[i] = cnt;
                     }
 
                     if(edgeOrient==eBackwards)
                     {
                         swap( maparray[0] , maparray[1] );
 
                         for(i = 3; i < P; i+=2)
                         {
                             signarray[i] = -1;
                         }
                     }
                     break;
                 }
                 case 1:
                 {
                     maparray[0] = order1;
                     maparray[1] = 1;
                     for(i = 2; i < P; i++)
                     {
                         maparray[i] = order1-1+i;
                     }
 
                     if(edgeOrient==eBackwards)
                     {
                         swap( maparray[0] , maparray[1] );
 
                         for(i = 3; i < P; i+=2)
                         {
                             signarray[i] = -1;
                         }
                     }
                     break;
                 }
                 case 2:
                 {
                     for(i = 0; i < P; i++)
                     {
                         maparray[i] = i;
                     }
 
                     if(edgeOrient==eForwards)
                     {
                         swap( maparray[0] , maparray[1] );
 
                         for(i = 3; i < P; i+=2)
                         {
                             signarray[i] = -1;
                         }
                     }
                     break;
                 }
             default:
                 ASSERTL0(false,"eid must be between 0 and 2");
                 break;
             }
 
 
             if (checkForZeroedModes)
             {
                 // Zero signmap and set maparray to zero if
                 // elemental modes are not as large as face modes
                 for (int j = numModes; j < P; j++)
                 {
                     signarray[j] = 0.0;
                     maparray[j]  = maparray[0];
                 }
             }
         }

void Nektar::StdRegions::StdTriExp::v_GetInteriorMap ( Array< OneD, unsigned int > & outarray )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 1191 of file StdTriExp.cpp.

References ASSERTL1, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetBasisType(), Nektar::StdRegions::StdExpansion::GetNcoeffs(), Nektar::StdRegions::StdExpansion::m_base, and Nektar::StdRegions::StdExpansion::NumBndryCoeffs().

Referenced by v_FwdTrans_BndConstrained().

         {
             ASSERTL1(GetBasisType(0) == LibUtilities::eModified_A &&
                      GetBasisType(1) == LibUtilities::eModified_B,
                      "Expansion not of a proper type");
 
             int i,j;
             int cnt = 0;
             int nummodes0, nummodes1;
             int startvalue;
             if(outarray.num_elements()!=GetNcoeffs()-NumBndryCoeffs())
             {
                 outarray = Array<OneD, unsigned int>(GetNcoeffs()-NumBndryCoeffs());
             }
 
             nummodes0 = m_base[0]->GetNumModes();
             nummodes1 = m_base[1]->GetNumModes();
 
             startvalue = 2*nummodes1;
 
             for(i = 0; i < nummodes0-2; i++)
             {
                 for(j = 0; j < nummodes1-3-i; j++)
                 {
                     outarray[cnt++]=startvalue+j;
                 }
                 startvalue+=nummodes1-2-i;
             }
         }

int Nektar::StdRegions::StdTriExp::v_GetNedges ( ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 746 of file StdTriExp.cpp.

         {
             return 3;
         }

int Nektar::StdRegions::StdTriExp::v_GetNverts ( ) const

protectedvirtual

Implements Nektar::StdRegions::StdExpansion.

Definition at line 741 of file StdTriExp.cpp.

         {
             return 3;
         }

void Nektar::StdRegions::StdTriExp::v_GetSimplexEquiSpacedConnectivity	(	Array< OneD, int > &	conn,
		bool	standard = `true`
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1610 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::m_base.

         {
             int np1 = m_base[0]->GetNumPoints();
             int np2 = m_base[1]->GetNumPoints();
             int np = max(np1,np2);
 
             conn = Array<OneD, int>(3*(np-1)*(np-1));
 
             int row   = 0;
             int rowp1 = 0;
             int cnt = 0;
             for(int i = 0; i < np-1; ++i)
             {
                 rowp1 += np-i;
                 for(int j = 0; j < np-i-2; ++j)
                 {
                     conn[cnt++] = row   +j;
                     conn[cnt++] = row   +j+1;
                     conn[cnt++] = rowp1 +j;
 
                     conn[cnt++] = rowp1 +j+1;
                     conn[cnt++] = rowp1 +j;
                     conn[cnt++] = row   +j+1;
                 }
 
                 conn[cnt++] = row  +np-i-2;
                 conn[cnt++] = row  +np-i-1;
                 conn[cnt++] = rowp1+np-i-2;
 
                 row += np-i;
             }
         }

int Nektar::StdRegions::StdTriExp::v_GetVertexMap	(	int	localVertexId,
		bool	useCoeffPacking = `false`
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 1041 of file StdTriExp.cpp.

References ASSERTL0, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetEdgeBasisType(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             ASSERTL0(
                 GetEdgeBasisType(localVertexId) == LibUtilities::eModified_A ||
                 GetEdgeBasisType(localVertexId) == LibUtilities::eModified_B,
                 "Mapping not defined for this type of basis");
 
             int localDOF = 0;
             if(useCoeffPacking == true)
             {
                 switch(localVertexId)
                 {
                 case 0:
                     {
                         localDOF = 0;
                         break;
                     }
                 case 1:
                     {
                         localDOF = 1;
                         break;
                     }
                 case 2:
                     {
                         localDOF = m_base[1]->GetNumModes();
                         break;
                     }
                 default:
                     {
                         ASSERTL0(false,"eid must be between 0 and 2");
                         break;
                     }
                 }
             }
             else // follow book format for vertex indexing.
             {
                 switch(localVertexId)
                 {
                 case 0:
                     {
                         localDOF = 0;
                         break;
                     }
                 case 1:
                     {
                         localDOF = m_base[1]->GetNumModes();
                         break;
                     }
                 case 2:
                     {
                         localDOF = 1;
                         break;
                     }
                 default:
                     {
                         ASSERTL0(false,"eid must be between 0 and 2");
                         break;
                     }
                 }
             }
 
             return localDOF;
         }

void Nektar::StdRegions::StdTriExp::v_HelmholtzMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 1381 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion2D::v_HelmholtzMatrixOp_MatFree().

         {
             StdTriExp::v_HelmholtzMatrixOp_MatFree(inarray,outarray,mkey);
         }

NekDouble Nektar::StdRegions::StdTriExp::v_Integral ( const Array< OneD, const NekDouble > & inarray )

protectedvirtual

Integrates the specified function over the domain.

See also: StdRegions::StdExpansion::Integral.

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, and Nektar::LocalRegions::TriExp.

Definition at line 82 of file StdTriExp.cpp.

References Nektar::LibUtilities::eGaussRadauMAlpha1Beta0, Nektar::StdRegions::StdExpansion::GetPointsType(), Nektar::StdRegions::StdExpansion2D::Integral(), Nektar::StdRegions::StdExpansion::m_base, and Vmath::Smul().

         {
             int    i;
             int nquad1 = m_base[1]->GetNumPoints();
             Array<OneD, NekDouble> w1_tmp(nquad1);
 
             Array<OneD, const NekDouble> w0 = m_base[0]->GetW();
             Array<OneD, const NekDouble> w1 = m_base[1]->GetW();
             Array<OneD, const NekDouble> z1 = m_base[1]->GetZ();
 
             switch(m_base[1]->GetPointsType())
             {
             case LibUtilities::eGaussRadauMAlpha1Beta0: // (0,1) Jacobi Inner product
                 {
                     Vmath::Smul(nquad1, 0.5, w1, 1, w1_tmp,1);
                     break;
                 }
             default:
                 {
                     // include jacobian factor on whatever coordinates are defined.
                     for(i = 0; i < nquad1; ++i)
                     {
                         w1_tmp[i] = 0.5*(1-z1[i])*w1[i];
                     }
                     break;
                 }
             }
 
             return StdExpansion2D::Integral(inarray,w0,w1_tmp);
         }

void Nektar::StdRegions::StdTriExp::v_IProductWRTBase	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Calculate the inner product of inarray with respect to the basis B=base0[p]*base1[pq] and put into outarray.

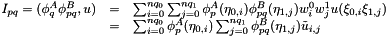
$\begin{array}{rcl} I_{pq} = (\phi^A_q \phi^B_{pq}, u) &=& \sum_{i=0}^{nq_0}\sum_{j=0}^{nq_1} \phi^A_p(\eta_{0,i})\phi^B_{pq}(\eta_{1,j}) w^0_i w^1_j u(\xi_{0,i} \xi_{1,j}) \\ & = & \sum_{i=0}^{nq_0} \phi^A_p(\eta_{0,i}) \sum_{j=0}^{nq_1} \phi^B_{pq}(\eta_{1,j}) \tilde{u}_{i,j} \end{array}$

where

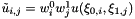
$\tilde{u}_{i,j} = w^0_i w^1_j u(\xi_{0,i},\xi_{1,j})$

which can be implemented as

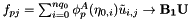
$f_{pj} = \sum_{i=0}^{nq_0} \phi^A_p(\eta_{0,i}) \tilde{u}_{i,j} \rightarrow {\bf B_1 U}$ $I_{pq} = \sum_{j=0}^{nq_1} \phi^B_{pq}(\eta_{1,j}) f_{pj} \rightarrow {\bf B_2[p*skip] f[skip]}$

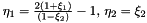
Recall: $\eta_{1} = \frac{2(1+\xi_1)}{(1-\xi_2)}-1, \, \eta_2 = \xi_2$

Note: For the orthgonality of this expansion to be realised the 'q' ordering must run fastest in contrast to the Quad and Hex ordering where 'p' index runs fastest to be consistent with the quadrature ordering.

In the triangular space the i (i.e. 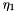$\eta_1$ direction) ordering still runs fastest by convention.

Implements Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 466 of file StdTriExp.cpp.

References v_IProductWRTBase_SumFac().

Referenced by v_FwdTrans(), and v_FwdTrans_BndConstrained().

         {
             StdTriExp::v_IProductWRTBase_SumFac(inarray,outarray);
         }

void Nektar::StdRegions::StdTriExp::v_IProductWRTBase_MatOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented in Nektar::LocalRegions::TriExp.

Definition at line 473 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eIProductWRTBase, Nektar::StdRegions::StdExpansion::GetStdMatrix(), Nektar::StdRegions::StdExpansion::GetTotPoints(), and Nektar::StdRegions::StdExpansion::m_ncoeffs.

         {
             int nq = GetTotPoints();
             StdMatrixKey      iprodmatkey(eIProductWRTBase,DetShapeType(),*this);
             DNekMatSharedPtr  iprodmat = GetStdMatrix(iprodmatkey);
 
             Blas::Dgemv('N',m_ncoeffs,nq,1.0,iprodmat->GetPtr().get(),
                         m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
         }

void Nektar::StdRegions::StdTriExp::v_IProductWRTBase_SumFac	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		bool	multiplybyweights = `true`
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 485 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion2D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, and Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric().

Referenced by v_IProductWRTBase(), and Nektar::StdRegions::StdNodalTriExp::v_IProductWRTBase_SumFac().

         {
             int    nquad0 = m_base[0]->GetNumPoints();
             int    nquad1 = m_base[1]->GetNumPoints();
             int    order0 = m_base[0]->GetNumModes();
 
             if(multiplybyweights)
             {
                 Array<OneD,NekDouble> tmp(nquad0*nquad1+nquad1*order0);
                 Array<OneD,NekDouble> wsp(tmp+nquad0*nquad1);
 
                 // multiply by integration constants
                 MultiplyByQuadratureMetric(inarray,tmp);
                 IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
                                              m_base[1]->GetBdata(),
                                              tmp,outarray,wsp);
             }
             else
             {
                 Array<OneD,NekDouble> wsp(nquad1*order0);
                 IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
                                              m_base[1]->GetBdata(),
                                              inarray,outarray,wsp);
             }
         }

void Nektar::StdRegions::StdTriExp::v_IProductWRTBase_SumFacKernel	(	const Array< OneD, const NekDouble > &	base0,
		const Array< OneD, const NekDouble > &	base1,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		Array< OneD, NekDouble > &	wsp,
		bool	doCheckCollDir0,
		bool	doCheckCollDir1
	)

protectedvirtual

Implements Nektar::StdRegions::StdExpansion2D.

Definition at line 514 of file StdTriExp.cpp.

References ASSERTL1, Vmath::Ddot(), Nektar::LibUtilities::eModified_A, Nektar::StdRegions::StdExpansion::GetBasisType(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             int i;
             int mode;
             int nquad0  = m_base[0]->GetNumPoints();
             int nquad1  = m_base[1]->GetNumPoints();   
             int nmodes0 = m_base[0]->GetNumModes();
             int nmodes1 = m_base[1]->GetNumModes();
 
             ASSERTL1(wsp.num_elements() >= nquad1*nmodes0,
                      "Workspace size is not sufficient");
 
             Blas::Dgemm('T','N',nquad1,nmodes0,nquad0,1.0,inarray.get(),nquad0,
                         base0.get(),nquad0,0.0,wsp.get(),nquad1);
 
             // Inner product with respect to 'b' direction
             for (mode=i=0; i < nmodes0; ++i)
             {
                 Blas::Dgemv('T',nquad1,nmodes1-i,1.0, base1.get()+mode*nquad1,
                             nquad1,wsp.get()+i*nquad1,1, 0.0,
                             outarray.get() + mode,1);
                 mode += nmodes1 - i;
             }
 
             // fix for modified basis by splitting top vertex mode
             if (m_base[0]->GetBasisType() == LibUtilities::eModified_A)
             {
                 outarray[1] += Blas::Ddot(nquad1,base1.get()+nquad1,1,
                                           wsp.get()+nquad1,1);
             }
         }

void Nektar::StdRegions::StdTriExp::v_IProductWRTDerivBase	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::StdRegions::StdNodalTriExp, and Nektar::LocalRegions::TriExp.

Definition at line 553 of file StdTriExp.cpp.

References v_IProductWRTDerivBase_SumFac().

         {
             StdTriExp::v_IProductWRTDerivBase_SumFac(dir,inarray,outarray);
         }

void Nektar::StdRegions::StdTriExp::v_IProductWRTDerivBase_MatOp	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented in Nektar::LocalRegions::TriExp.

Definition at line 561 of file StdTriExp.cpp.

References ASSERTL1, Nektar::StdRegions::StdExpansion::DetShapeType(), Nektar::StdRegions::eIProductWRTDerivBase0, Nektar::StdRegions::eIProductWRTDerivBase1, Nektar::StdRegions::StdExpansion::GetStdMatrix(), Nektar::StdRegions::StdExpansion::GetTotPoints(), and Nektar::StdRegions::StdExpansion::m_ncoeffs.

         {
             int nq = GetTotPoints();
             MatrixType mtype = eIProductWRTDerivBase0;
 
             switch(dir)
             {
                 case 0:
                 {
                     mtype = eIProductWRTDerivBase0;
                     break;
                 }
                 case 1:
                 {
                     mtype = eIProductWRTDerivBase1;
                     break;
                 }
                 default:
                 {
                     ASSERTL1(false,"input dir is out of range");
                     break;
                 }
             }
 
             StdMatrixKey      iprodmatkey(mtype,DetShapeType(),*this);
             DNekMatSharedPtr  iprodmat = GetStdMatrix(iprodmatkey);
 
             Blas::Dgemv('N',m_ncoeffs,nq,1.0,iprodmat->GetPtr().get(),
                         m_ncoeffs, inarray.get(), 1, 0.0, outarray.get(), 1);
         }

void Nektar::StdRegions::StdTriExp::v_IProductWRTDerivBase_SumFac	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 595 of file StdTriExp.cpp.

References ASSERTL1, Nektar::StdRegions::StdExpansion2D::IProductWRTBase_SumFacKernel(), Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion::m_ncoeffs, Nektar::StdRegions::StdExpansion::MultiplyByQuadratureMetric(), Vmath::Smul(), Vmath::Vadd(), and Vmath::Vmul().

Referenced by v_IProductWRTDerivBase(), and Nektar::StdRegions::StdNodalTriExp::v_IProductWRTDerivBase_SumFac().

         {
             int    i;
             int    nquad0  = m_base[0]->GetNumPoints();
             int    nquad1  = m_base[1]->GetNumPoints();
             int    nqtot   = nquad0*nquad1;
             int    nmodes0 = m_base[0]->GetNumModes();
             int    wspsize = max(max(nqtot,m_ncoeffs),nquad1*nmodes0);
 
             Array<OneD, NekDouble> gfac0(2*wspsize);
             Array<OneD, NekDouble> tmp0 (gfac0+wspsize);
 
             const Array<OneD, const NekDouble>& z1 = m_base[1]->GetZ();
 
             // set up geometric factor: 2/(1-z1)
             for(i = 0; i < nquad1; ++i)
             {
                 gfac0[i] = 2.0/(1-z1[i]);
             }
 
             for(i = 0; i < nquad1; ++i)
             {
                 Vmath::Smul(nquad0,gfac0[i],&inarray[0]+i*nquad0,1,
                             &tmp0[0]+i*nquad0,1);
             }
 
             MultiplyByQuadratureMetric(tmp0,tmp0);
 
             switch(dir)
             {
                 case 0:
                 {
                     IProductWRTBase_SumFacKernel(m_base[0]->GetDbdata(),
                                                  m_base[1]->GetBdata(),
                                                  tmp0,outarray,gfac0);
                     break;
                 }
                 case 1:
                 {
                     Array<OneD, NekDouble> tmp3(m_ncoeffs);
                     const Array<OneD, const NekDouble>& z0 = m_base[0]->GetZ();
 
                     for (i = 0; i < nquad0; ++i)
                     {
                         gfac0[i] = 0.5*(1+z0[i]);
                     }
 
                     for (i = 0; i < nquad1; ++i)
                     {
                         Vmath::Vmul(nquad0,&gfac0[0],1,&tmp0[0]+i*nquad0,1,
                                     &tmp0[0]+i*nquad0,1);
                     }
 
                     IProductWRTBase_SumFacKernel(m_base[0]->GetDbdata(),
                                                  m_base[1]->GetBdata(),
                                                  tmp0,tmp3,gfac0);
 
                     MultiplyByQuadratureMetric(inarray,tmp0);
                     IProductWRTBase_SumFacKernel(m_base[0]->GetBdata(),
                                                  m_base[1]->GetDbdata(),
                                                  tmp0,outarray,gfac0);
                     Vmath::Vadd(m_ncoeffs,&tmp3[0],1,&outarray[0],1,
                                 &outarray[0],1);
                     break;
                 }
                 default:
                 {
                     ASSERTL1(false, "input dir is out of range");
                     break;
                 }
             }
         }

bool Nektar::StdRegions::StdTriExp::v_IsBoundaryInteriorExpansion ( )

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 851 of file StdTriExp.cpp.

References Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, and Nektar::StdRegions::StdExpansion::m_base.

         {
             return m_base[0]->GetBasisType() == LibUtilities::eModified_A &&
                    m_base[1]->GetBasisType() == LibUtilities::eModified_B;
         }

void Nektar::StdRegions::StdTriExp::v_LaplacianMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 1353 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion2D::v_LaplacianMatrixOp_MatFree().

         {
             StdTriExp::v_LaplacianMatrixOp_MatFree(inarray,outarray,mkey);
         }

void Nektar::StdRegions::StdTriExp::v_LaplacianMatrixOp	(	const int	k1,
		const int	k2,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 1361 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::LaplacianMatrixOp_MatFree().

         {
             StdExpansion::LaplacianMatrixOp_MatFree(
                 k1,k2,inarray,outarray,mkey);
         }

void Nektar::StdRegions::StdTriExp::v_LocCoordToLocCollapsed	(	const Array< OneD, const NekDouble > &	xi,
		Array< OneD, NekDouble > &	eta
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 675 of file StdTriExp.cpp.

References Nektar::NekConstants::kNekZeroTol.

         {
 
             // set up local coordinate system
             if (fabs(xi[1]-1.0) < NekConstants::kNekZeroTol)
             {
                 eta[0] = -1.0;
                 eta[1] =  1.0;
             }
             else
             {
                 eta[0] = 2*(1+xi[0])/(1-xi[1])-1.0;
                 eta[1] = xi[1];
             }
         }

void Nektar::StdRegions::StdTriExp::v_MassMatrixOp	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 1345 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::MassMatrixOp_MatFree().

         {
             StdExpansion::MassMatrixOp_MatFree(inarray,outarray,mkey);
         }

void Nektar::StdRegions::StdTriExp::v_MultiplyByStdQuadratureMetric	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 1565 of file StdTriExp.cpp.

References ASSERTL0, Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::eGaussRadauMAlpha1Beta0, Nektar::LibUtilities::ePolyEvenlySpaced, Nektar::StdRegions::StdExpansion::GetPointsType(), Nektar::StdRegions::StdExpansion::m_base, and Vmath::Vmul().

         {
             int    i;
             int    nquad0 = m_base[0]->GetNumPoints();
             int    nquad1 = m_base[1]->GetNumPoints();
 
             const Array<OneD, const NekDouble>& w0 = m_base[0]->GetW();
             const Array<OneD, const NekDouble>& w1 = m_base[1]->GetW();
             const Array<OneD, const NekDouble>& z1 = m_base[1]->GetZ();
 
             // multiply by integration constants
             for(i = 0; i < nquad1; ++i)
             {
                 Vmath::Vmul(nquad0,inarray.get()+i*nquad0,1,
                             w0.get(),1, outarray.get()+i*nquad0,1);
             }
 
             switch(m_base[1]->GetPointsType())
             {
                 // Legendre inner product
                 case LibUtilities::ePolyEvenlySpaced:
                 case LibUtilities::eGaussLobattoLegendre:
                     for(i = 0; i < nquad1; ++i)
                     {
                         Blas::Dscal(nquad0,0.5*(1-z1[i])*w1[i],
                                     outarray.get()+i*nquad0,1);
                     }
                     break;
 
                 // (1,0) Jacobi Inner product
                 case LibUtilities::eGaussRadauMAlpha1Beta0:
                     for(i = 0; i < nquad1; ++i)
                     {
                         Blas::Dscal(nquad0,0.5*w1[i],outarray.get()+i*nquad0,1);
                     }
                     break;
 
                 default:
                     ASSERTL0(false, "Unsupported quadrature points type.");
                     break;
             }
         }

int Nektar::StdRegions::StdTriExp::v_NumBndryCoeffs ( ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::StdRegions::StdNodalTriExp.

Definition at line 756 of file StdTriExp.cpp.

References ASSERTL1, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetBasisNumModes(), and Nektar::StdRegions::StdExpansion::GetBasisType().

Referenced by v_FwdTrans_BndConstrained().

         {
             ASSERTL1(GetBasisType(0) == LibUtilities::eModified_A,
                      "BasisType is not a boundary interior form");
             ASSERTL1(GetBasisType(1) == LibUtilities::eModified_B,
                      "BasisType is not a boundary interior form");
 
             return 3 + (GetBasisNumModes(0)-2) + 2*(GetBasisNumModes(1)-2);
         }

int Nektar::StdRegions::StdTriExp::v_NumDGBndryCoeffs ( ) const

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 766 of file StdTriExp.cpp.

References ASSERTL1, Nektar::LibUtilities::eModified_A, Nektar::LibUtilities::eModified_B, Nektar::StdRegions::StdExpansion::GetBasisNumModes(), and Nektar::StdRegions::StdExpansion::GetBasisType().

         {
             ASSERTL1(GetBasisType(0) == LibUtilities::eModified_A,
                      "BasisType is not a boundary interior form");
             ASSERTL1(GetBasisType(1) == LibUtilities::eModified_B,
                      "BasisType is not a boundary interior form");
 
             return GetBasisNumModes(0) + 2*GetBasisNumModes(1);
         }

void Nektar::StdRegions::StdTriExp::v_PhysDeriv	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	out_d0,
		Array< OneD, NekDouble > &	out_d1,
		Array< OneD, NekDouble > &	out_d2 = `NullNekDouble1DArray`
	)

protectedvirtual

Calculate the derivative of the physical points.

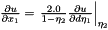
$\frac{\partial u}{\partial x_1} = \left . \frac{2.0}{1-\eta_2} \frac{\partial u}{\partial d\eta_1} \right |_{\eta_2}$

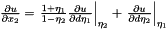
$\frac{\partial u}{\partial x_2} = \left . \frac{1+\eta_1}{1-\eta_2} \frac{\partial u}{\partial d\eta_1} \right |_{\eta_2} + \left . \frac{\partial u}{\partial d\eta_2} \right |_{\eta_1}$

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, and Nektar::LocalRegions::TriExp.

Definition at line 130 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::m_base, Nektar::StdRegions::StdExpansion2D::PhysTensorDeriv(), and Vmath::Vvtvp().

Referenced by v_PhysDeriv(), and v_StdPhysDeriv().

         {
             int    i;
             int    nquad0 = m_base[0]->GetNumPoints();
             int    nquad1 = m_base[1]->GetNumPoints();
             Array<OneD, NekDouble> wsp(nquad0*nquad1);
 
             const Array<OneD, const NekDouble>& z0 = m_base[0]->GetZ();
             const Array<OneD, const NekDouble>& z1 = m_base[1]->GetZ();
 
             // set up geometric factor: 2/(1-z1)
             for (i = 0; i < nquad1; ++i)
             {
                 wsp[i] = 2.0/(1-z1[i]);
             }
 
             if (out_d0.num_elements() > 0)
             {
                 PhysTensorDeriv(inarray, out_d0, out_d1);
 
                 for (i = 0; i < nquad1; ++i)
                 {
                     Blas::Dscal(nquad0,wsp[i],&out_d0[0]+i*nquad0,1);
                 }
 
                 // if no d1 required do not need to calculate both deriv
                 if (out_d1.num_elements() > 0)
                 {
                     // set up geometric factor: (1_z0)/(1-z1)
                     for (i = 0; i < nquad0; ++i)
                     {
                         wsp[i] = 0.5*(1+z0[i]);
                     }
 
                     for (i = 0; i < nquad1; ++i)
                     {
                         Vmath::Vvtvp(nquad0,&wsp[0],1,&out_d0[0]+i*nquad0,
                                      1,&out_d1[0]+i*nquad0,
                                      1,&out_d1[0]+i*nquad0,1);
                     }
                 }
             }
             else if (out_d1.num_elements() > 0)
             {
                 Array<OneD, NekDouble> diff0(nquad0*nquad1);
                 PhysTensorDeriv(inarray, diff0, out_d1);
 
                 for (i = 0; i < nquad1; ++i)
                 {
                     Blas::Dscal(nquad0,wsp[i],&diff0[0]+i*nquad0,1);
                 }
 
                 for (i = 0; i < nquad0; ++i)
                 {
                     wsp[i] = 0.5*(1+z0[i]);
                 }
 
                 for (i = 0; i < nquad1; ++i)
                 {
                     Vmath::Vvtvp(nquad0,&wsp[0],1,&diff0[0]+i*nquad0,
                                  1,&out_d1[0]+i*nquad0,
                                  1,&out_d1[0]+i*nquad0,1);
                 }
             }
         }

void Nektar::StdRegions::StdTriExp::v_PhysDeriv	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	out_d0
	)

protectedvirtual

Calculate the derivative of the physical points in a given direction.

See also: StdRegions::StdExpansion::PhysDeriv

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, and Nektar::LocalRegions::TriExp.

Definition at line 200 of file StdTriExp.cpp.

References ASSERTL1, Nektar::NullNekDouble1DArray, and v_PhysDeriv().

         {
             switch(dir)
             {
                 case 0:
                 {
                     v_PhysDeriv(inarray, outarray, NullNekDouble1DArray);
                     break;
                 }
                 case 1:
                 {
                     v_PhysDeriv(inarray, NullNekDouble1DArray, outarray);
                     break;
                 }
                 default:
                 {
                     ASSERTL1(false,"input dir is out of range");
                     break;
                 }
             }
         }

void Nektar::StdRegions::StdTriExp::v_ReduceOrderCoeffs	(	int	numMin,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::TriExp.

Definition at line 1482 of file StdTriExp.cpp.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr(), Nektar::LibUtilities::eGaussLobattoLegendre, Nektar::LibUtilities::eOrtho_A, Nektar::LibUtilities::eOrtho_B, Nektar::StdRegions::StdExpansion::GetBasisType(), and Nektar::StdRegions::StdExpansion::m_base.

         {
             int n_coeffs = inarray.num_elements();
             int nquad0   = m_base[0]->GetNumPoints();
             int nquad1   = m_base[1]->GetNumPoints();
             Array<OneD, NekDouble> coeff(n_coeffs);
             Array<OneD, NekDouble> coeff_tmp(n_coeffs,0.0);
             Array<OneD, NekDouble> tmp;
             Array<OneD, NekDouble> tmp2;
             int nqtot    = nquad0*nquad1;
             Array<OneD, NekDouble> phys_tmp(nqtot,0.0);
 
             int       nmodes0 = m_base[0]->GetNumModes();
             int       nmodes1 = m_base[1]->GetNumModes();
             int       numMin2 = nmodes0;
             int       i;
 
             const LibUtilities::PointsKey Pkey0(
                 nmodes0, LibUtilities::eGaussLobattoLegendre);
             const LibUtilities::PointsKey Pkey1(
                 nmodes1, LibUtilities::eGaussLobattoLegendre);
 
             LibUtilities::BasisKey b0(m_base[0]->GetBasisType(),nmodes0,Pkey0);
             LibUtilities::BasisKey b1(m_base[1]->GetBasisType(),nmodes1,Pkey1);
 
             LibUtilities::BasisKey bortho0(LibUtilities::eOrtho_A,nmodes0,Pkey0);
             LibUtilities::BasisKey bortho1(LibUtilities::eOrtho_B,nmodes1,Pkey1);
 
             StdRegions::StdTriExpSharedPtr m_OrthoTriExp;
             StdRegions::StdTriExpSharedPtr m_TriExp;
 
             m_TriExp      = MemoryManager<StdRegions::StdTriExp>
                 ::AllocateSharedPtr(b0,      b1);
             m_OrthoTriExp = MemoryManager<StdRegions::StdTriExp>
                 ::AllocateSharedPtr(bortho0, bortho1);
 
             m_TriExp     ->BwdTrans(inarray,phys_tmp);
             m_OrthoTriExp->FwdTrans(phys_tmp, coeff);
 
             for (i = 0; i < n_coeffs; i++)
             {
                 if (i == numMin)
                 {
                     coeff[i] = 0.0;
                     numMin += numMin2 - 1;
                     numMin2 -= 1.0;
                 }
             }
 
             m_OrthoTriExp->BwdTrans(coeff,phys_tmp);
             m_TriExp     ->FwdTrans(phys_tmp, outarray);
 
         }

void Nektar::StdRegions::StdTriExp::v_StdPhysDeriv	(	const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	out_d0,
		Array< OneD, NekDouble > &	out_d1,
		Array< OneD, NekDouble > &	out_d2 = `NullNekDouble1DArray`
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp.

Definition at line 225 of file StdTriExp.cpp.

References v_PhysDeriv().

         {
             StdTriExp::v_PhysDeriv(inarray, out_d0, out_d1);
         }

void Nektar::StdRegions::StdTriExp::v_StdPhysDeriv	(	const int	dir,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Definition at line 234 of file StdTriExp.cpp.

References v_PhysDeriv().

         {
             StdTriExp::v_PhysDeriv(dir,inarray,outarray);
         }

void Nektar::StdRegions::StdTriExp::v_SVVLaplacianFilter	(	Array< OneD, NekDouble > &	array,
		const StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::TriExp.

Definition at line 1390 of file StdTriExp.cpp.

         {
             int qa = m_base[0]->GetNumPoints();
             int qb = m_base[1]->GetNumPoints();
             int nmodes_a = m_base[0]->GetNumModes();
             int nmodes_b = m_base[1]->GetNumModes();
             int nmodes = min(nmodes_a,nmodes_b);
 
             // Declare orthogonal basis.
             LibUtilities::PointsKey pa(qa,m_base[0]->GetPointsType());
             LibUtilities::PointsKey pb(qb,m_base[1]->GetPointsType());
 
             LibUtilities::BasisKey Ba(LibUtilities::eOrtho_A,nmodes_a,pa);
             LibUtilities::BasisKey Bb(LibUtilities::eOrtho_B,nmodes_b,pb);
             StdTriExp OrthoExp(Ba,Bb);
 
             NekDouble  SvvDiffCoeff  = mkey.GetConstFactor(eFactorSVVDiffCoeff);
 
             Array<OneD, NekDouble> orthocoeffs(OrthoExp.GetNcoeffs());
 
 
             if(mkey.HasVarCoeff(eVarCoeffLaplacian)) // Rodrigo's svv mapping 
             {
                 Array<OneD, NekDouble> sqrt_varcoeff(qa*qb);
                 Array<OneD, NekDouble> tmp(qa*qb);
 
                 Vmath::Vsqrt(qa * qb,
                              mkey.GetVarCoeff(eVarCoeffLaplacian), 1,
                              sqrt_varcoeff,                        1);
 
                 // multiply by sqrt(Variable Coefficient) containing h v /p
                 Vmath::Vmul(qa*qb,sqrt_varcoeff,1,array,1,tmp,1);
 
                 // project onto modal  space.
                 OrthoExp.FwdTrans(tmp,orthocoeffs);
 
                 int cnt = 0;
                 for(int j = 0; j < nmodes_a; ++j)
                 {
                     for(int k = 0; k < nmodes_b-j; ++k, ++cnt)
                     {
                         orthocoeffs[cnt] *=
                             (1.0 + SvvDiffCoeff
                                 *pow(j/(nmodes_a-1)+k/(nmodes_b-1),0.5*nmodes));
                     }
                 }
 
                 // backward transform to physical space
                 OrthoExp.BwdTrans(orthocoeffs,tmp);
 
                 // multiply by sqrt(Variable Coefficient) containing h v /p
                 // - split to keep symmetry
                 Vmath::Vmul(qa*qb,sqrt_varcoeff,1,tmp,1,array,1);
             }
             else
             {
                 int j, k , cnt = 0;
                 int cutoff = (int) (mkey.GetConstFactor(eFactorSVVCutoffRatio)*
                                                         min(nmodes_a,nmodes_b));
 
                 NekDouble epsilon = 1.0;
                 int nmodes = min(nmodes_a,nmodes_b);
 
                 // project onto physical space.
                 OrthoExp.FwdTrans(array,orthocoeffs);
 
                 // apply SVV filter (JEL)
                 for(j = 0; j < nmodes_a; ++j)
                 {
                     for(k = 0; k < nmodes_b-j; ++k)
                     {
                         if(j + k >= cutoff)
                         {
                             orthocoeffs[cnt] *= (SvvDiffCoeff
                                 *exp(-(j+k-nmodes)*(j+k-nmodes)
                                     /((NekDouble)((j+k-cutoff+epsilon)
                                             *(j+k-cutoff+epsilon)))));
                         }
                         else
                         {
                             orthocoeffs[cnt] *= 0.0;
                         }
                         cnt++;
                     }
                 }
 
                 // backward transform to physical space
                 OrthoExp.BwdTrans(orthocoeffs,array);
             }
         }

void Nektar::StdRegions::StdTriExp::v_WeakDerivMatrixOp	(	const int	i,
		const Array< OneD, const NekDouble > &	inarray,
		Array< OneD, NekDouble > &	outarray,
		const StdMatrixKey &	mkey
	)

protectedvirtual

Reimplemented from Nektar::StdRegions::StdExpansion.

Reimplemented in Nektar::LocalRegions::NodalTriExp, Nektar::LocalRegions::TriExp, and Nektar::StdRegions::StdNodalTriExp.

Definition at line 1372 of file StdTriExp.cpp.

References Nektar::StdRegions::StdExpansion::WeakDerivMatrixOp_MatFree().

         {
             StdExpansion::WeakDerivMatrixOp_MatFree(i,inarray,outarray,mkey);
         }

Public Member Functions

Protected Member Functions

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation