|
Nektar++
|
|
Nektar++
|
A class to assist in the construction of nodal simplex and hybrid elements in two and three dimensions. More...
#include <NodalUtil.h>
Public Member Functions | |
| NekVector< NekDouble > | GetWeights () |
| Obtain the integration weights for the given nodal distribution. More... | |
| SharedMatrix | GetVandermonde () |
| Return the Vandermonde matrix for the nodal distribution. More... | |
| SharedMatrix | GetVandermondeForDeriv (int dir) |
| Return the Vandermonde matrix of the derivative of the basis functions for the nodal distribution. More... | |
| SharedMatrix | GetDerivMatrix (int dir) |
| Return the derivative matrix for the nodal distribution. More... | |
| SharedMatrix | GetInterpolationMatrix (Array< OneD, Array< OneD, NekDouble > > &xi) |
Construct the interpolation matrix used to evaluate the basis at the points xi inside the element. More... | |
Protected Member Functions | |
| NodalUtil (int degree, int dim) | |
| Set up the NodalUtil object. More... | |
| virtual NekVector< NekDouble > | v_OrthoBasis (const int mode)=0 |
| Return the values of the orthogonal basis at the nodal points for a given mode. More... | |
| virtual NekVector< NekDouble > | v_OrthoBasisDeriv (const int dir, const int mode)=0 |
| Return the values of the derivative of the orthogonal basis at the nodal points for a given mode. More... | |
| virtual boost::shared_ptr < NodalUtil > | v_CreateUtil (Array< OneD, Array< OneD, NekDouble > > &xi)=0 |
| Construct a NodalUtil object of the appropriate element type for a given set of points. More... | |
| virtual NekDouble | v_ModeZeroIntegral ()=0 |
| Return the value of the integral of the zero-th mode for this element. More... | |
| virtual int | v_NumModes ()=0 |
| Calculate the number of degrees of freedom for this element. More... | |
Protected Attributes | |
| int | m_dim |
| Dimension of the nodal element. More... | |
| int | m_degree |
| Degree of the nodal element. More... | |
| int | m_numPoints |
| Total number of nodal points. More... | |
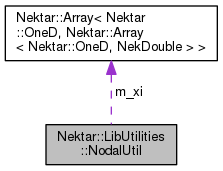
| Array< OneD, Array< OneD, NekDouble > > | m_xi |
| Coordinates of the nodal points defining the basis. More... | |
A class to assist in the construction of nodal simplex and hybrid elements in two and three dimensions.
The NodalUtil class and its subclasses are designed to take care of some common issues that arise when considering triangles, tetrahedra and prismatic elements that are equipped with a nodal Lagrangian basis, defined using a set of nodal points 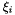 that we store in the array NodalUtil::m_xi. Since one cannot write this basis analytically, we instead construct the Vandermonde matrix
that we store in the array NodalUtil::m_xi. Since one cannot write this basis analytically, we instead construct the Vandermonde matrix
![\[ \mathbf{V}_{ij} = \psi_j(\xi_i) \]](form_105.png)
where 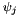 is a basis that spans the polynomial space of the element. The Vandermonde matrix can then be used to construct the integration weights, derivative and interpolation matrices. Although this can be any basis, such as the monomial basis
is a basis that spans the polynomial space of the element. The Vandermonde matrix can then be used to construct the integration weights, derivative and interpolation matrices. Although this can be any basis, such as the monomial basis 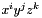 , in practice this is numerically unstable at high polynomial orders. Elements are therefore expected to use the 'traditional' modal orthogonal basis. See Sherwin & Karniadakis or Hesthaven & Warburton for further details of this basis and the surrounding numerical issues.
, in practice this is numerically unstable at high polynomial orders. Elements are therefore expected to use the 'traditional' modal orthogonal basis. See Sherwin & Karniadakis or Hesthaven & Warburton for further details of this basis and the surrounding numerical issues.
This class therefore contains the generic logic needed to construct various matrices, and subclasses override virtual functions that define the orthogonal basis and its derivatives for a particular element type.
Definition at line 84 of file NodalUtil.h.
|
inlineprotected |
Set up the NodalUtil object.
| dim | Dimension of the element. |
| degree | Polynomial degree of the element. |
Definition at line 101 of file NodalUtil.h.
| SharedMatrix Nektar::LibUtilities::NodalUtil::GetDerivMatrix | ( | int | dir | ) |
Return the derivative matrix for the nodal distribution.
This routine constructs and returns the derivative matrices 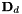 for coordinate directions
for coordinate directions 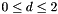 , which can be used to evaluate the derivative of a nodal expansion at the points defined by NodalUtil::m_xi. These are calculated as
, which can be used to evaluate the derivative of a nodal expansion at the points defined by NodalUtil::m_xi. These are calculated as 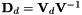 , where
, where 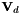 is the derivative Vandermonde matrix and
is the derivative Vandermonde matrix and 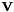 is the Vandermonde matrix.
is the Vandermonde matrix.
| dir | Coordinate direction in which to evaluate the derivative. |
dir. Definition at line 168 of file NodalUtil.cpp.
References GetVandermonde(), and GetVandermondeForDeriv().
| SharedMatrix Nektar::LibUtilities::NodalUtil::GetInterpolationMatrix | ( | Array< OneD, Array< OneD, NekDouble > > & | xi | ) |
Construct the interpolation matrix used to evaluate the basis at the points xi inside the element.
This routine returns a matrix 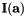 that can be used to evaluate the nodal basis at the points defined by the parameter
that can be used to evaluate the nodal basis at the points defined by the parameter xi, which is denoted by 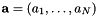 and
and 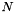 is the number of points in
is the number of points in xi.
In particular, if the array 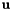 with components
with components 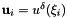 represents the polynomial approximation of a function
represents the polynomial approximation of a function 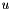 evaluated at the nodal points NodalUtil::m_xi, then the evaluation of
evaluated at the nodal points NodalUtil::m_xi, then the evaluation of 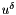 evaluated at the input points
evaluated at the input points 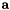 is given by
is given by 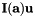 .
.
| xi | An array of first size number of spatial dimensions 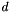 and secondary size the number of points to interpolate. and secondary size the number of points to interpolate. |
xi. Definition at line 202 of file NodalUtil.cpp.
References GetVandermonde(), and v_CreateUtil().
Referenced by Nektar::Utilities::ProcessVarOpti::BuildDerivUtil().
| SharedMatrix Nektar::LibUtilities::NodalUtil::GetVandermonde | ( | ) |
Return the Vandermonde matrix for the nodal distribution.
This routine constructs and returns the Vandermonde matrix 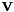 , with each entry as
, with each entry as 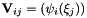 where
where 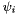 is the orthogonal basis obtained through the abstract function NodalUtil::v_OrthoBasis.
is the orthogonal basis obtained through the abstract function NodalUtil::v_OrthoBasis.
Definition at line 102 of file NodalUtil.cpp.
References m_numPoints, v_NumModes(), and v_OrthoBasis().
Referenced by Nektar::Utilities::ProcessVarOpti::BuildDerivUtil(), GetDerivMatrix(), GetInterpolationMatrix(), GetWeights(), and Nektar::NekMeshUtils::BLMesh::Setup().
| SharedMatrix Nektar::LibUtilities::NodalUtil::GetVandermondeForDeriv | ( | int | dir | ) |
Return the Vandermonde matrix of the derivative of the basis functions for the nodal distribution.
This routine constructs and returns the Vandermonde matrix for the derivative of the basis functions 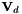 for coordinate directions
for coordinate directions 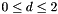 , with each entry as
, with each entry as 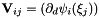 where
where 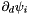 is the derivative of the orthogonal basis obtained through the abstract function NodalUtil::v_OrthoBasisDeriv.
is the derivative of the orthogonal basis obtained through the abstract function NodalUtil::v_OrthoBasisDeriv.
| dir | Direction of derivative in the standard element. |
dir. Definition at line 135 of file NodalUtil.cpp.
References m_numPoints, v_NumModes(), and v_OrthoBasisDeriv().
Referenced by Nektar::Utilities::ProcessVarOpti::BuildDerivUtil(), GetDerivMatrix(), and Nektar::NekMeshUtils::BLMesh::Setup().
Obtain the integration weights for the given nodal distribution.
This routine constructs the integration weights for the given nodal distribution inside NodalUtil::m_xi. To do this we solve the linear system 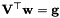 where
where 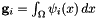 , and we use the fact that under the definition of the orthogonal basis for each element type,
, and we use the fact that under the definition of the orthogonal basis for each element type, 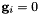 for
for 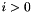 . We use NodalUtil::v_ModeZeroIntegral to return the analytic value of
. We use NodalUtil::v_ModeZeroIntegral to return the analytic value of 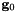 .
.
Definition at line 66 of file NodalUtil.cpp.
References GetVandermonde(), m_numPoints, Nektar::LinearSystem::SolveTranspose(), v_ModeZeroIntegral(), and v_NumModes().
|
protectedpure virtual |
Construct a NodalUtil object of the appropriate element type for a given set of points.
This function is used inside NodalUtil::GetInterpolationMatrix so that the (potentially non-square) Vandermonde matrix can be constructed to create the interpolation matrix at an arbitrary set of points in the domain.
| xi | Distribution of nodal points to create utility with. |
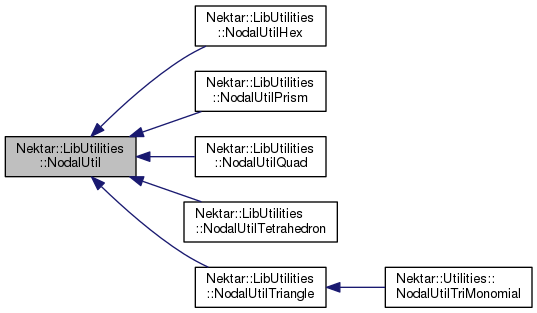
Implemented in Nektar::Utilities::NodalUtilTriMonomial, Nektar::LibUtilities::NodalUtilHex, Nektar::LibUtilities::NodalUtilQuad, Nektar::LibUtilities::NodalUtilPrism, Nektar::LibUtilities::NodalUtilTetrahedron, and Nektar::LibUtilities::NodalUtilTriangle.
Referenced by GetInterpolationMatrix().
|
protectedpure virtual |
Return the value of the integral of the zero-th mode for this element.
Note that for the orthogonal basis under consideration, all modes integrate to zero asides from the zero-th mode. This function is used in NodalUtil::GetWeights to determine integration weights.
Implemented in Nektar::LibUtilities::NodalUtilHex, Nektar::LibUtilities::NodalUtilQuad, Nektar::LibUtilities::NodalUtilPrism, Nektar::LibUtilities::NodalUtilTetrahedron, and Nektar::LibUtilities::NodalUtilTriangle.
Referenced by GetWeights().
|
protectedpure virtual |
Calculate the number of degrees of freedom for this element.
Implemented in Nektar::LibUtilities::NodalUtilHex, Nektar::LibUtilities::NodalUtilQuad, Nektar::LibUtilities::NodalUtilPrism, Nektar::LibUtilities::NodalUtilTetrahedron, and Nektar::LibUtilities::NodalUtilTriangle.
Referenced by GetVandermonde(), GetVandermondeForDeriv(), and GetWeights().
|
protectedpure virtual |
Return the values of the orthogonal basis at the nodal points for a given mode.
| mode | Mode number, which is between 0 and NodalUtil::v_NumModes()
|
mode evaluated at the nodal points. Implemented in Nektar::Utilities::NodalUtilTriMonomial, Nektar::LibUtilities::NodalUtilHex, Nektar::LibUtilities::NodalUtilQuad, Nektar::LibUtilities::NodalUtilPrism, Nektar::LibUtilities::NodalUtilTetrahedron, and Nektar::LibUtilities::NodalUtilTriangle.
Referenced by GetVandermonde().
|
protectedpure virtual |
Return the values of the derivative of the orthogonal basis at the nodal points for a given mode.
| dir | Coordinate direction of derivative. |
| mode | Mode number, which is between 0 and NodalUtil::v_NumModes()
|
Implemented in Nektar::Utilities::NodalUtilTriMonomial, Nektar::LibUtilities::NodalUtilHex, Nektar::LibUtilities::NodalUtilQuad, Nektar::LibUtilities::NodalUtilPrism, Nektar::LibUtilities::NodalUtilTetrahedron, and Nektar::LibUtilities::NodalUtilTriangle.
Referenced by GetVandermondeForDeriv().
|
protected |
Degree of the nodal element.
Definition at line 108 of file NodalUtil.h.
Referenced by Nektar::LibUtilities::NodalUtilHex::NodalUtilHex(), Nektar::LibUtilities::NodalUtilPrism::NodalUtilPrism(), Nektar::LibUtilities::NodalUtilQuad::NodalUtilQuad(), Nektar::LibUtilities::NodalUtilTetrahedron::NodalUtilTetrahedron(), Nektar::LibUtilities::NodalUtilTriangle::NodalUtilTriangle(), Nektar::LibUtilities::NodalUtilTriangle::v_CreateUtil(), Nektar::LibUtilities::NodalUtilTetrahedron::v_CreateUtil(), Nektar::LibUtilities::NodalUtilPrism::v_CreateUtil(), Nektar::LibUtilities::NodalUtilQuad::v_CreateUtil(), Nektar::LibUtilities::NodalUtilHex::v_CreateUtil(), Nektar::Utilities::NodalUtilTriMonomial::v_CreateUtil(), Nektar::LibUtilities::NodalUtilTriangle::v_NumModes(), Nektar::LibUtilities::NodalUtilTetrahedron::v_NumModes(), Nektar::LibUtilities::NodalUtilPrism::v_NumModes(), Nektar::LibUtilities::NodalUtilQuad::v_NumModes(), and Nektar::LibUtilities::NodalUtilHex::v_NumModes().
|
protected |
Dimension of the nodal element.
Definition at line 106 of file NodalUtil.h.
|
protected |
Total number of nodal points.
Definition at line 110 of file NodalUtil.h.
Referenced by GetVandermonde(), GetVandermondeForDeriv(), GetWeights(), Nektar::LibUtilities::NodalUtilHex::NodalUtilHex(), Nektar::LibUtilities::NodalUtilPrism::NodalUtilPrism(), Nektar::LibUtilities::NodalUtilQuad::NodalUtilQuad(), Nektar::LibUtilities::NodalUtilTetrahedron::NodalUtilTetrahedron(), Nektar::LibUtilities::NodalUtilTriangle::NodalUtilTriangle(), Nektar::LibUtilities::NodalUtilTriangle::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilTetrahedron::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilPrism::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilQuad::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilHex::v_OrthoBasis(), Nektar::Utilities::NodalUtilTriMonomial::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilTriangle::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilTetrahedron::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilPrism::v_OrthoBasisDeriv(), Nektar::LibUtilities::NodalUtilQuad::v_OrthoBasisDeriv(), and Nektar::LibUtilities::NodalUtilHex::v_OrthoBasisDeriv().
Coordinates of the nodal points defining the basis.
Definition at line 112 of file NodalUtil.h.
Referenced by Nektar::LibUtilities::NodalUtilHex::NodalUtilHex(), Nektar::LibUtilities::NodalUtilPrism::NodalUtilPrism(), Nektar::LibUtilities::NodalUtilQuad::NodalUtilQuad(), Nektar::LibUtilities::NodalUtilTetrahedron::NodalUtilTetrahedron(), Nektar::LibUtilities::NodalUtilTriangle::NodalUtilTriangle(), Nektar::LibUtilities::NodalUtilQuad::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilHex::v_OrthoBasis(), Nektar::Utilities::NodalUtilTriMonomial::v_OrthoBasis(), Nektar::LibUtilities::NodalUtilQuad::v_OrthoBasisDeriv(), and Nektar::LibUtilities::NodalUtilHex::v_OrthoBasisDeriv().
 1.8.8
1.8.8