Nektar++
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Pages
Public Member Functions | Static Public Member Functions | Static Public Attributes | Protected Member Functions | Protected Attributes | Friends | List of all members
Nektar::CompressibleFlowSystem Class Reference

#include <CompressibleFlowSystem.h>

Inheritance diagram for Nektar::CompressibleFlowSystem:
Inheritance graph
[legend]
Collaboration diagram for Nektar::CompressibleFlowSystem:
Collaboration graph
[legend]

Public Member Functions

virtual ~CompressibleFlowSystem ()
 Destructor for CompressibleFlowSystem class. More...
 
NekDouble GetStabilityLimit (int n)
 Function to calculate the stability limit for DG/CG. More...
 
Array< OneD, NekDouble > GetStabilityLimitVector (const Array< OneD, int > &ExpOrder)
 Function to calculate the stability limit for DG/CG (a vector of them). More...
 
- Public Member Functions inherited from Nektar::SolverUtils::UnsteadySystem
virtual SOLVER_UTILS_EXPORT ~UnsteadySystem ()
 Destructor. More...
 
SOLVER_UTILS_EXPORT NekDouble GetTimeStep (const Array< OneD, const Array< OneD, NekDouble > > &inarray)
 Calculate the larger time-step mantaining the problem stable. More...
 
- Public Member Functions inherited from Nektar::SolverUtils::EquationSystem
virtual SOLVER_UTILS_EXPORT ~EquationSystem ()
 Destructor. More...
 
SOLVER_UTILS_EXPORT void SetUpTraceNormals (void)
 
SOLVER_UTILS_EXPORT void InitObject ()
 Initialises the members of this object. More...
 
SOLVER_UTILS_EXPORT void DoInitialise ()
 Perform any initialisation necessary before solving the problem. More...
 
SOLVER_UTILS_EXPORT void DoSolve ()
 Solve the problem. More...
 
SOLVER_UTILS_EXPORT void TransCoeffToPhys ()
 Transform from coefficient to physical space. More...
 
SOLVER_UTILS_EXPORT void TransPhysToCoeff ()
 Transform from physical to coefficient space. More...
 
SOLVER_UTILS_EXPORT void Output ()
 Perform output operations after solve. More...
 
SOLVER_UTILS_EXPORT NekDouble LinfError (unsigned int field, const Array< OneD, NekDouble > &exactsoln=NullNekDouble1DArray)
 Linf error computation. More...
 
SOLVER_UTILS_EXPORT std::string GetSessionName ()
 Get Session name. More...
 
template<class T >
boost::shared_ptr< T > as ()
 
SOLVER_UTILS_EXPORT void ResetSessionName (std::string newname)
 Reset Session name. More...
 
SOLVER_UTILS_EXPORT
LibUtilities::SessionReaderSharedPtr 		GetSession ()
 Get Session name. More...
 
SOLVER_UTILS_EXPORT
MultiRegions::ExpListSharedPtr 		GetPressure ()
 Get pressure field if available. More...
 
SOLVER_UTILS_EXPORT void PrintSummary (std::ostream &out)
 Print a summary of parameters and solver characteristics. More...
 
SOLVER_UTILS_EXPORT void SetLambda (NekDouble lambda)
 Set parameter m_lambda. More...
 
SOLVER_UTILS_EXPORT void EvaluateFunction (Array< OneD, Array< OneD, NekDouble > > &pArray, std::string pFunctionName, const NekDouble pTime=0.0, const int domain=0)
 Evaluates a function as specified in the session file. More...
 
SOLVER_UTILS_EXPORT void EvaluateFunction (std::vector< std::string > pFieldNames, Array< OneD, Array< OneD, NekDouble > > &pFields, const std::string &pName, const NekDouble &pTime=0.0, const int domain=0)
 Populate given fields with the function from session. More...
 
SOLVER_UTILS_EXPORT void EvaluateFunction (std::vector< std::string > pFieldNames, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields, const std::string &pName, const NekDouble &pTime=0.0, const int domain=0)
 Populate given fields with the function from session. More...
 
SOLVER_UTILS_EXPORT void EvaluateFunction (std::string pFieldName, Array< OneD, NekDouble > &pArray, const std::string &pFunctionName, const NekDouble &pTime=0.0, const int domain=0)
 
SOLVER_UTILS_EXPORT std::string DescribeFunction (std::string pFieldName, const std::string &pFunctionName, const int domain)
 Provide a description of a function for a given field name. More...
 
SOLVER_UTILS_EXPORT void InitialiseBaseFlow (Array< OneD, Array< OneD, NekDouble > > &base)
 Perform initialisation of the base flow. More...
 
SOLVER_UTILS_EXPORT void SetInitialConditions (NekDouble initialtime=0.0, bool dumpInitialConditions=true, const int domain=0)
 Initialise the data in the dependent fields. More...
 
SOLVER_UTILS_EXPORT void EvaluateExactSolution (int field, Array< OneD, NekDouble > &outfield, const NekDouble time)
 Evaluates an exact solution. More...
 
SOLVER_UTILS_EXPORT NekDouble L2Error (unsigned int field, const Array< OneD, NekDouble > &exactsoln, bool Normalised=false)
 Compute the L2 error between fields and a given exact solution. More...
 
SOLVER_UTILS_EXPORT NekDouble L2Error (unsigned int field, bool Normalised=false)
 Compute the L2 error of the fields. More...
 
SOLVER_UTILS_EXPORT Array
< OneD, NekDouble > 		ErrorExtraPoints (unsigned int field)
 Compute error (L2 and L_inf) over an larger set of quadrature points return [L2 Linf]. More...
 
SOLVER_UTILS_EXPORT void WeakAdvectionGreensDivergenceForm (const Array< OneD, Array< OneD, NekDouble > > &F, Array< OneD, NekDouble > &outarray)
 Compute the inner product 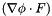$ (\nabla \phi \cdot F) $. More...
 
SOLVER_UTILS_EXPORT void WeakAdvectionDivergenceForm (const Array< OneD, Array< OneD, NekDouble > > &F, Array< OneD, NekDouble > &outarray)
 Compute the inner product 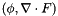$ (\phi, \nabla \cdot F) $. More...
 
SOLVER_UTILS_EXPORT void WeakAdvectionNonConservativeForm (const Array< OneD, Array< OneD, NekDouble > > &V, const Array< OneD, const NekDouble > &u, Array< OneD, NekDouble > &outarray, bool UseContCoeffs=false)
 Compute the inner product 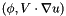$ (\phi, V\cdot \nabla u) $. More...
 
f SOLVER_UTILS_EXPORT void AdvectionNonConservativeForm (const Array< OneD, Array< OneD, NekDouble > > &V, const Array< OneD, const NekDouble > &u, Array< OneD, NekDouble > &outarray, Array< OneD, NekDouble > &wk=NullNekDouble1DArray)
 Compute the non-conservative advection. More...
 
SOLVER_UTILS_EXPORT void WeakDGAdvection (const Array< OneD, Array< OneD, NekDouble > > &InField, Array< OneD, Array< OneD, NekDouble > > &OutField, bool NumericalFluxIncludesNormal=true, bool InFieldIsInPhysSpace=false, int nvariables=0)
 Calculate the weak discontinuous Galerkin advection. More...
 
SOLVER_UTILS_EXPORT void WeakDGDiffusion (const Array< OneD, Array< OneD, NekDouble > > &InField, Array< OneD, Array< OneD, NekDouble > > &OutField, bool NumericalFluxIncludesNormal=true, bool InFieldIsInPhysSpace=false)
 Calculate weak DG Diffusion in the LDG form. More...
 
SOLVER_UTILS_EXPORT void Checkpoint_Output (const int n)
 Write checkpoint file of m_fields. More...
 
SOLVER_UTILS_EXPORT void Checkpoint_Output (const int n, MultiRegions::ExpListSharedPtr &field, std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)
 Write checkpoint file of custom data fields. More...
 
SOLVER_UTILS_EXPORT void Checkpoint_BaseFlow (const int n)
 Write base flow file of m_fields. More...
 
SOLVER_UTILS_EXPORT void WriteFld (const std::string &outname)
 Write field data to the given filename. More...
 
SOLVER_UTILS_EXPORT void WriteFld (const std::string &outname, MultiRegions::ExpListSharedPtr &field, std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)
 Write input fields to the given filename. More...
 
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields)
 Input field data from the given file. More...
 
SOLVER_UTILS_EXPORT void ImportFldToMultiDomains (const std::string &infile, Array< OneD, MultiRegions::ExpListSharedPtr > &pFields, const int ndomains)
 Input field data from the given file to multiple domains. More...
 
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, std::vector< std::string > &fieldStr, Array< OneD, Array< OneD, NekDouble > > &coeffs)
 Output a field. Input field data into array from the given file. More...
 
SOLVER_UTILS_EXPORT void ImportFld (const std::string &infile, MultiRegions::ExpListSharedPtr &pField, std::string &pFieldName)
 Output a field. Input field data into ExpList from the given file. More...
 
SOLVER_UTILS_EXPORT void ScanForHistoryPoints ()
 Builds map of which element holds each history point. More...
 
SOLVER_UTILS_EXPORT void WriteHistoryData (std::ostream &out)
 Probe each history point and write to file. More...
 
SOLVER_UTILS_EXPORT void SessionSummary (SummaryList &vSummary)
 Write out a session summary. More...
 
SOLVER_UTILS_EXPORT Array
< OneD,
MultiRegions::ExpListSharedPtr > & 		UpdateFields ()
 
SOLVER_UTILS_EXPORT
LibUtilities::FieldMetaDataMap & 		UpdateFieldMetaDataMap ()
 Get hold of FieldInfoMap so it can be updated. More...
 
SOLVER_UTILS_EXPORT NekDouble GetFinalTime ()
 Return final time. More...
 
SOLVER_UTILS_EXPORT int GetNcoeffs ()
 
SOLVER_UTILS_EXPORT int GetNcoeffs (const int eid)
 
SOLVER_UTILS_EXPORT int GetNumExpModes ()
 
SOLVER_UTILS_EXPORT const
Array< OneD, int > 		GetNumExpModesPerExp ()
 
SOLVER_UTILS_EXPORT int GetNvariables ()
 
SOLVER_UTILS_EXPORT const
std::string 		GetVariable (unsigned int i)
 
SOLVER_UTILS_EXPORT int GetTraceTotPoints ()
 
SOLVER_UTILS_EXPORT int GetTraceNpoints ()
 
SOLVER_UTILS_EXPORT int GetExpSize ()
 
SOLVER_UTILS_EXPORT int GetPhys_Offset (int n)
 
SOLVER_UTILS_EXPORT int GetCoeff_Offset (int n)
 
SOLVER_UTILS_EXPORT int GetTotPoints ()
 
SOLVER_UTILS_EXPORT int GetTotPoints (int n)
 
SOLVER_UTILS_EXPORT int GetNpoints ()
 
SOLVER_UTILS_EXPORT int GetNumElmVelocity ()
 
SOLVER_UTILS_EXPORT int GetSteps ()
 
SOLVER_UTILS_EXPORT NekDouble GetTimeStep ()
 
SOLVER_UTILS_EXPORT void CopyFromPhysField (const int i, Array< OneD, NekDouble > &output)
 
SOLVER_UTILS_EXPORT void CopyToPhysField (const int i, Array< OneD, NekDouble > &output)
 
SOLVER_UTILS_EXPORT void SetSteps (const int steps)
 
SOLVER_UTILS_EXPORT void ZeroPhysFields ()
 
SOLVER_UTILS_EXPORT void FwdTransFields ()
 
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &flux)
 
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &fluxX, Array< OneD, Array< OneD, NekDouble > > &fluxY)
 
SOLVER_UTILS_EXPORT void GetFluxVector (const int i, const int j, Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &flux)
 
SOLVER_UTILS_EXPORT void NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numflux)
 
SOLVER_UTILS_EXPORT void NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numfluxX, Array< OneD, Array< OneD, NekDouble > > &numfluxY)
 
SOLVER_UTILS_EXPORT void NumFluxforScalar (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &uflux)
 
SOLVER_UTILS_EXPORT void NumFluxforVector (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &qfield, Array< OneD, Array< OneD, NekDouble > > &qflux)
 
SOLVER_UTILS_EXPORT void SetModifiedBasis (const bool modbasis)
 
SOLVER_UTILS_EXPORT int NoCaseStringCompare (const string &s1, const string &s2)
 Perform a case-insensitive string comparison. More...
 
SOLVER_UTILS_EXPORT int GetCheckpointNumber ()
 
SOLVER_UTILS_EXPORT void SetCheckpointNumber (int num)
 
SOLVER_UTILS_EXPORT int GetCheckpointSteps ()
 
SOLVER_UTILS_EXPORT void SetCheckpointSteps (int num)
 
SOLVER_UTILS_EXPORT void SetTime (const NekDouble time)
 
SOLVER_UTILS_EXPORT void SetInitialStep (const int step)
 
SOLVER_UTILS_EXPORT void SetBoundaryConditions (NekDouble time)
 Evaluates the boundary conditions at the given time. More...
 
virtual SOLVER_UTILS_EXPORT bool v_NegatedOp ()
 Virtual function to identify if operator is negated in DoSolve. More...
 

Static Public Member Functions

static
SolverUtils::EquationSystemSharedPtr 		create (const LibUtilities::SessionReaderSharedPtr &pSession)
 Creates an instance of this class. More...
 

Static Public Attributes

static std::string className
 Name of class. More...
 

Protected Member Functions

 CompressibleFlowSystem (const LibUtilities::SessionReaderSharedPtr &pSession)
 
virtual void v_InitObject ()
 Initialization object for CompressibleFlowSystem class. More...
 
virtual void v_GenerateSummary (SolverUtils::SummaryList &s)
 Print a summary of time stepping parameters. More...
 
void GetFluxVector (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &flux)
 Return the flux vector for the compressible Euler equations. More...
 
void GetFluxVectorDeAlias (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &flux)
 Return the flux vector for the compressible Euler equations by using the de-aliasing technique. More...
 
void GetViscousFluxVector (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &derivatives, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &viscousTensor)
 Return the flux vector for the LDG diffusion problem. More...
 
void GetFluxVectorPDESC (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &flux)
 
void GetViscousFluxVectorDeAlias (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &derivatives, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &viscousTensor)
 Return the flux vector for the LDG diffusion problem. More...
 
void SetCommonBC (const std::string &userDefStr, const int n, const NekDouble time, int &cnt, Array< OneD, Array< OneD, NekDouble > > &inarray)
 Set boundary conditions which can be: a) Wall and Symmerty BCs implemented at CompressibleFlowSystem level since they are compressible solver specific; b) Time dependent BCs. More...
 
void WallBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Wall boundary conditions for compressible flow problems. More...
 
void WallViscousBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Wall boundary conditions for viscous compressible flow problems. More...
 
void SymmetryBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Symmetry boundary conditions for compressible flow problems. More...
 
void RiemannInvariantBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Outflow characteristic boundary conditions for compressible flow problems. More...
 
void PressureOutflowNonReflectiveBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Pressure outflow non-reflective boundary conditions for compressible flow problems. More...
 
void PressureOutflowBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Pressure outflow boundary conditions for compressible flow problems. More...
 
void PressureOutflowFileBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Pressure outflow boundary conditions for compressible flow problems. More...
 
void PressureInflowFileBC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Pressure inflow boundary conditions for compressible flow problems where either the density and the velocities are assigned from a file or the full state is assigned from a file (depending on the problem type, either subsonic or supersonic). More...
 
void ExtrapOrder0BC (int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
 Extrapolation of order 0 for all the variables such that, at the boundaries, a trivial Riemann problem is solved. More...
 
void GetVelocityVector (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &velocity)
 
void GetSoundSpeed (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &pressure, Array< OneD, NekDouble > &soundspeed)
 
void GetMach (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &soundspeed, Array< OneD, NekDouble > &mach)
 
void GetTemperature (const Array< OneD, const Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &pressure, Array< OneD, NekDouble > &temperature)
 
void GetPressure (const Array< OneD, const Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &pressure)
 Calculate the pressure field 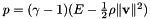$ p = (\gamma-1)(E-\frac{1}{2}\rho\| \mathbf{v} \|^2) $ assuming an ideal gas law. More...
 
void GetPressure (const Array< OneD, const Array< OneD, NekDouble > > &physfield, const Array< OneD, const Array< OneD, NekDouble > > &velocity, Array< OneD, NekDouble > &pressure)
 
void GetEnthalpy (const Array< OneD, const Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &pressure, Array< OneD, NekDouble > &enthalpy)
 
void GetEntropy (const Array< OneD, const Array< OneD, NekDouble > > &physfield, const Array< OneD, const NekDouble > &pressure, const Array< OneD, const NekDouble > &temperature, Array< OneD, NekDouble > &entropy)
 
void GetSmoothArtificialViscosity (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &eps_bar)
 
void GetDynamicViscosity (const Array< OneD, const NekDouble > &temperature, Array< OneD, NekDouble > &mu)
 
void GetStdVelocity (const Array< OneD, const Array< OneD, NekDouble > > &inarray, Array< OneD, NekDouble > &stdV)
 
virtual bool v_PostIntegrate (int step)
 
bool CalcSteadyState (bool output)
 
void GetSensor (const Array< OneD, const Array< OneD, NekDouble > > &physarray, Array< OneD, NekDouble > &Sensor, Array< OneD, NekDouble > &SensorKappa)
 
void GetElementDimensions (Array< OneD, Array< OneD, NekDouble > > &outarray, Array< OneD, NekDouble > &hmin)
 
void GetAbsoluteVelocity (const Array< OneD, const Array< OneD, NekDouble > > &inarray, Array< OneD, NekDouble > &Vtot)
 
void GetArtificialDynamicViscosity (const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &mu_var)
 
void SetVarPOrderElmt (const Array< OneD, const Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &PolyOrder)
 
void GetForcingTerm (const Array< OneD, const Array< OneD, NekDouble > > &inarray, Array< OneD, Array< OneD, NekDouble > > outarrayForcing)
 
virtual NekDouble v_GetTimeStep (const Array< OneD, const Array< OneD, NekDouble > > &inarray)
 Return the timestep to be used for the next step in the time-marching loop. More...
 
virtual void v_SetInitialConditions (NekDouble initialtime=0.0, bool dumpInitialConditions=true, const int domain=0)
 
NekDouble GetGasConstant ()
 
NekDouble GetGamma ()
 
const Array< OneD, const Array
< OneD, NekDouble > > & 		GetVecLocs ()
 
const Array< OneD, const Array
< OneD, NekDouble > > & 		GetNormals ()
 
virtual void v_ExtraFldOutput (std::vector< Array< OneD, NekDouble > > &fieldcoeffs, std::vector< std::string > &variables)
 
- Protected Member Functions inherited from Nektar::SolverUtils::UnsteadySystem
SOLVER_UTILS_EXPORT UnsteadySystem (const LibUtilities::SessionReaderSharedPtr &pSession)
 Initialises UnsteadySystem class members. More...
 
SOLVER_UTILS_EXPORT NekDouble MaxTimeStepEstimator ()
 Get the maximum timestep estimator for cfl control. More...
 
virtual SOLVER_UTILS_EXPORT void v_DoSolve ()
 Solves an unsteady problem. More...
 
virtual SOLVER_UTILS_EXPORT void v_DoInitialise ()
 Sets up initial conditions. More...
 
virtual SOLVER_UTILS_EXPORT void v_AppendOutput1D (Array< OneD, Array< OneD, NekDouble > > &solution1D)
 Print the solution at each solution point in a txt file. More...
 
virtual SOLVER_UTILS_EXPORT void v_NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numflux)
 
virtual SOLVER_UTILS_EXPORT void v_NumericalFlux (Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &numfluxX, Array< OneD, Array< OneD, NekDouble > > &numfluxY)
 
virtual SOLVER_UTILS_EXPORT void v_NumFluxforScalar (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &uflux)
 
virtual SOLVER_UTILS_EXPORT void v_NumFluxforVector (const Array< OneD, Array< OneD, NekDouble > > &ufield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &qfield, Array< OneD, Array< OneD, NekDouble > > &qflux)
 
virtual SOLVER_UTILS_EXPORT bool v_PreIntegrate (int step)
 
virtual SOLVER_UTILS_EXPORT bool v_SteadyStateCheck (int step)
 
SOLVER_UTILS_EXPORT void CheckForRestartTime (NekDouble &time)
 
SOLVER_UTILS_EXPORT void SVVVarDiffCoeff (const Array< OneD, Array< OneD, NekDouble > > vel, StdRegions::VarCoeffMap &varCoeffMap)
 Evaluate the SVV diffusion coefficient according to Moura's paper where it should proportional to h time velocity. More...
 
- Protected Member Functions inherited from Nektar::SolverUtils::EquationSystem
SOLVER_UTILS_EXPORT EquationSystem (const LibUtilities::SessionReaderSharedPtr &pSession)
 Initialises EquationSystem class members. More...
 
int nocase_cmp (const string &s1, const string &s2)
 
virtual SOLVER_UTILS_EXPORT
NekDouble 		v_LinfError (unsigned int field, const Array< OneD, NekDouble > &exactsoln=NullNekDouble1DArray)
 Virtual function for the L_inf error computation between fields and a given exact solution. More...
 
virtual SOLVER_UTILS_EXPORT
NekDouble 		v_L2Error (unsigned int field, const Array< OneD, NekDouble > &exactsoln=NullNekDouble1DArray, bool Normalised=false)
 Virtual function for the L_2 error computation between fields and a given exact solution. More...
 
virtual SOLVER_UTILS_EXPORT void v_TransCoeffToPhys ()
 Virtual function for transformation to physical space. More...
 
virtual SOLVER_UTILS_EXPORT void v_TransPhysToCoeff ()
 Virtual function for transformation to coefficient space. More...
 
virtual SOLVER_UTILS_EXPORT void v_EvaluateExactSolution (unsigned int field, Array< OneD, NekDouble > &outfield, const NekDouble time)
 
SOLVER_UTILS_EXPORT void SetUpBaseFields (SpatialDomains::MeshGraphSharedPtr &mesh)
 
SOLVER_UTILS_EXPORT void ImportFldBase (std::string pInfile, SpatialDomains::MeshGraphSharedPtr pGraph)
 
virtual SOLVER_UTILS_EXPORT void v_Output (void)
 
virtual SOLVER_UTILS_EXPORT
MultiRegions::ExpListSharedPtr 		v_GetPressure (void)
 

Protected Attributes

SolverUtils::RiemannSolverSharedPtr m_riemannSolver
 
SolverUtils::RiemannSolverSharedPtr m_riemannSolverLDG
 
SolverUtils::AdvectionSharedPtr m_advection
 
SolverUtils::DiffusionSharedPtr m_diffusion
 
Array< OneD, Array< OneD,
NekDouble > > 		m_vecLocs
 
NekDouble m_gamma
 
NekDouble m_pInf
 
NekDouble m_rhoInf
 
NekDouble m_uInf
 
NekDouble m_vInf
 
NekDouble m_wInf
 
NekDouble m_UInf
 
NekDouble m_gasConstant
 
NekDouble m_Twall
 
std::string m_ViscosityType
 
std::string m_shockCaptureType
 
std::string m_EqTypeStr
 
NekDouble m_mu
 
NekDouble m_Skappa
 
NekDouble m_Kappa
 
NekDouble m_mu0
 
NekDouble m_FacL
 
NekDouble m_FacH
 
NekDouble m_eps_max
 
NekDouble m_thermalConductivity
 
NekDouble m_Cp
 
NekDouble m_C1
 
NekDouble m_C2
 
NekDouble m_hFactor
 
NekDouble m_Prandtl
 
NekDouble m_amplitude
 
NekDouble m_omega
 
std::ofstream m_errFile
 
int m_steadyStateSteps
 
NekDouble m_steadyStateTol
 
std::vector
< SolverUtils::ForcingSharedPtr > 		m_forcing
 
StdRegions::StdQuadExpSharedPtr m_OrthoQuadExp
 
StdRegions::StdHexExpSharedPtr m_OrthoHexExp
 
bool m_smoothDiffusion
 
Array< OneD, NekDouble > m_pressureStorage
 
Array< OneD, Array< OneD,
NekDouble > > 		m_fieldStorage
 
Array< OneD, Array< OneD,
NekDouble > > 		m_un
 
- Protected Attributes inherited from Nektar::SolverUtils::UnsteadySystem
int m_infosteps
 Number of time steps between outputting status information. More...
 
LibUtilities::TimeIntegrationWrapperSharedPtr m_intScheme
 Wrapper to the time integration scheme. More...
 
LibUtilities::TimeIntegrationSchemeOperators m_ode
 The time integration scheme operators to use. More...
 
LibUtilities::TimeIntegrationSolutionSharedPtr m_intSoln
 
NekDouble m_epsilon
 
bool m_explicitDiffusion
 Indicates if explicit or implicit treatment of diffusion is used. More...
 
bool m_explicitAdvection
 Indicates if explicit or implicit treatment of advection is used. More...
 
bool m_explicitReaction
 Indicates if explicit or implicit treatment of reaction is used. More...
 
bool m_homoInitialFwd
 Flag to determine if simulation should start in homogeneous forward transformed state. More...
 
std::vector< int > m_intVariables
 
std::vector< FilterSharedPtr > m_filters
 
- Protected Attributes inherited from Nektar::SolverUtils::EquationSystem
LibUtilities::CommSharedPtr m_comm
 Communicator. More...
 
LibUtilities::SessionReaderSharedPtr m_session
 The session reader. More...
 
LibUtilities::FieldIOSharedPtr m_fld
 Field input/output. More...
 
map< std::string, Array< OneD,
Array< OneD, float > > > 		m_interpWeights
 Map of the interpolation weights for a specific filename. More...
 
map< std::string, Array< OneD,
Array< OneD, unsigned int > > > 		m_interpInds
 Map of the interpolation indices for a specific filename. More...
 
Array< OneD,
MultiRegions::ExpListSharedPtr > 		m_fields
 Array holding all dependent variables. More...
 
Array< OneD,
MultiRegions::ExpListSharedPtr > 		m_base
 Base fields. More...
 
Array< OneD,
MultiRegions::ExpListSharedPtr > 		m_derivedfields
 Array holding all dependent variables. More...
 
SpatialDomains::BoundaryConditionsSharedPtr m_boundaryConditions
 Pointer to boundary conditions object. More...
 
SpatialDomains::MeshGraphSharedPtr m_graph
 Pointer to graph defining mesh. More...
 
std::string m_sessionName
 Name of the session. More...
 
NekDouble m_time
 Current time of simulation. More...
 
int m_initialStep
 Number of the step where the simulation should begin. More...
 
NekDouble m_fintime
 Finish time of the simulation. More...
 
NekDouble m_timestep
 Time step size. More...
 
NekDouble m_lambda
 Lambda constant in real system if one required. More...
 
std::set< std::string > m_loadedFields
 
NekDouble m_checktime
 Time between checkpoints. More...
 
int m_nchk
 Number of checkpoints written so far. More...
 
int m_steps
 Number of steps to take. More...
 
int m_checksteps
 Number of steps between checkpoints. More...
 
int m_spacedim
 Spatial dimension (>= expansion dim). More...
 
int m_expdim
 Expansion dimension. More...
 
bool m_singleMode
 Flag to determine if single homogeneous mode is used. More...
 
bool m_halfMode
 Flag to determine if half homogeneous mode is used. More...
 
bool m_multipleModes
 Flag to determine if use multiple homogenenous modes are used. More...
 
bool m_useFFT
 Flag to determine if FFT is used for homogeneous transform. More...
 
bool m_homogen_dealiasing
 Flag to determine if dealiasing is used for homogeneous simulations. More...
 
bool m_specHP_dealiasing
 Flag to determine if dealisising is usde for the Spectral/hp element discretisation. More...
 
enum MultiRegions::ProjectionType m_projectionType
 Type of projection; e.g continuous or discontinuous. More...
 
Array< OneD, Array< OneD,
NekDouble > > 		m_traceNormals
 Array holding trace normals for DG simulations in the forwards direction. More...
 
Array< OneD, Array< OneD,
Array< OneD, NekDouble > > > 		m_gradtan
 1 x nvariable x nq More...
 
Array< OneD, Array< OneD,
Array< OneD, NekDouble > > > 		m_tanbasis
 2 x m_spacedim x nq More...
 
Array< OneD, bool > m_checkIfSystemSingular
 Flag to indicate if the fields should be checked for singularity. More...
 
LibUtilities::FieldMetaDataMap m_fieldMetaDataMap
 Map to identify relevant solver info to dump in output fields. More...
 
int m_NumQuadPointsError
 Number of Quadrature points used to work out the error. More...
 
enum HomogeneousType m_HomogeneousType
 
NekDouble m_LhomX
 physical length in X direction (if homogeneous) More...
 
NekDouble m_LhomY
 physical length in Y direction (if homogeneous) More...
 
NekDouble m_LhomZ
 physical length in Z direction (if homogeneous) More...
 
int m_npointsX
 number of points in X direction (if homogeneous) More...
 
int m_npointsY
 number of points in Y direction (if homogeneous) More...
 
int m_npointsZ
 number of points in Z direction (if homogeneous) More...
 
int m_HomoDirec
 number of homogenous directions More...
 
int m_NumMode
 Mode to use in case of single mode analysis. More...
 

Friends

class MemoryManager< CompressibleFlowSystem >
 

Additional Inherited Members

- Public Attributes inherited from Nektar::SolverUtils::UnsteadySystem
NekDouble m_cflSafetyFactor
 CFL safety factor (comprise between 0 to 1). More...
 
- Protected Types inherited from Nektar::SolverUtils::EquationSystem
enum  HomogeneousType { eHomogeneous1D, eHomogeneous2D, eHomogeneous3D, eNotHomogeneous }
 Parameter for homogeneous expansions. More...
 

Detailed Description

Definition at line 52 of file CompressibleFlowSystem.h.

Constructor & Destructor Documentation

Nektar::CompressibleFlowSystem::~CompressibleFlowSystem ( )
virtual

Destructor for CompressibleFlowSystem class.

Definition at line 300 of file CompressibleFlowSystem.cpp.

301  {
302 
303  }
Nektar::CompressibleFlowSystem::CompressibleFlowSystem ( const LibUtilities::SessionReaderSharedPtr &  pSession)
protected

Definition at line 54 of file CompressibleFlowSystem.cpp.

56  : UnsteadySystem(pSession)
57  {
58  }
Nektar::SolverUtils::UnsteadySystem::UnsteadySystem
SOLVER_UTILS_EXPORT UnsteadySystem(const LibUtilities::SessionReaderSharedPtr &pSession)
Initialises UnsteadySystem class members.
Definition: UnsteadySystem.cpp:65

Member Function Documentation

bool Nektar::CompressibleFlowSystem::CalcSteadyState ( bool  output)
protected
static SolverUtils::EquationSystemSharedPtr Nektar::CompressibleFlowSystem::create ( const LibUtilities::SessionReaderSharedPtr &  pSession)
inlinestatic

Creates an instance of this class.

Definition at line 59 of file CompressibleFlowSystem.h.

References Nektar::MemoryManager< DataType >::AllocateSharedPtr().

61  {
62  return MemoryManager<CompressibleFlowSystem>::
63  AllocateSharedPtr(pSession);
64  }
Nektar::MemoryManager::AllocateSharedPtr
static boost::shared_ptr< DataType > AllocateSharedPtr()
Allocate a shared pointer from the memory pool.
Definition: NekMemoryManager.hpp:235
void Nektar::CompressibleFlowSystem::ExtrapOrder0BC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Extrapolation of order 0 for all the variables such that, at the boundaries, a trivial Riemann problem is solved.

Definition at line 1572 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, and Nektar::SolverUtils::EquationSystem::m_spacedim.

Referenced by SetCommonBC().

1576  {
1577  int i, j;
1578  int e, pnt;
1579  int id1, id2, nBCEdgePts;
1580  int nTracePts = GetTraceTotPoints();
1581  int nVariables = physarray.num_elements();
1582  int nDimensions = m_spacedim;
1583 
1584  const Array<OneD, const int> &traceBndMap
1585  = m_fields[0]->GetTraceBndMap();
1586 
1587  // Get physical values of the forward trace
1588  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
1589  for (i = 0; i < nVariables; ++i)
1590  {
1591  Fwd[i] = Array<OneD, NekDouble>(nTracePts);
1592  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
1593  }
1594 
1595  int eMax;
1596 
1597  eMax = m_fields[0]->GetBndCondExpansions()[bcRegion]->GetExpSize();
1598 
1599  // Loop on bcRegions
1600  for (e = 0; e < eMax; ++e)
1601  {
1602  nBCEdgePts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1603  GetExp(e)->GetTotPoints();
1604  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1605  GetPhys_Offset(e) ;
1606  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
1607 
1608  // Loop on points of bcRegion 'e'
1609  for (i = 0; i < nBCEdgePts; i++)
1610  {
1611  pnt = id2+i;
1612 
1613  // Setting up bcs for density
1614  (m_fields[0]->GetBndCondExpansions()[bcRegion]->
1615  UpdatePhys())[id1+i] = Fwd[0][pnt];
1616 
1617  // Setting up bcs for velocities
1618  for (j = 1; j <=nDimensions; ++j)
1619  {
1620  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1621  UpdatePhys())[id1+i] = Fwd[j][pnt];
1622  }
1623 
1624  // Setting up bcs for energy
1625  (m_fields[nVariables-1]->GetBndCondExpansions()[bcRegion]->
1626  UpdatePhys())[id1+i] = Fwd[nVariables-1][pnt];
1627  }
1628  }
1629  }
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
void Nektar::CompressibleFlowSystem::GetAbsoluteVelocity ( const Array< OneD, const Array< OneD, NekDouble > > &  inarray,
Array< OneD, NekDouble > &  Vtot 
)
protected

Referenced by Nektar::EulerADCFE::DoOdeRhs().

void Nektar::CompressibleFlowSystem::GetArtificialDynamicViscosity ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  mu_var 
)
protected

Referenced by Nektar::EulerADCFE::v_InitObject(), and v_InitObject().

void Nektar::CompressibleFlowSystem::GetDynamicViscosity ( const Array< OneD, const NekDouble > &  temperature,
Array< OneD, NekDouble > &  mu 
)
protected

Referenced by GetViscousFluxVector(), and GetViscousFluxVectorDeAlias().

void Nektar::CompressibleFlowSystem::GetElementDimensions ( Array< OneD, Array< OneD, NekDouble > > &  outarray,
Array< OneD, NekDouble > &  hmin 
)
protected
void Nektar::CompressibleFlowSystem::GetEnthalpy ( const Array< OneD, const Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  pressure,
Array< OneD, NekDouble > &  enthalpy 
)
protected
void Nektar::CompressibleFlowSystem::GetEntropy ( const Array< OneD, const Array< OneD, NekDouble > > &  physfield,
const Array< OneD, const NekDouble > &  pressure,
const Array< OneD, const NekDouble > &  temperature,
Array< OneD, NekDouble > &  entropy 
)
protected
void Nektar::CompressibleFlowSystem::GetFluxVector ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  flux 
)
protected

Return the flux vector for the compressible Euler equations.

Parameters
iComponent of the flux vector to calculate.
physfieldFields.
fluxResulting flux.

Definition at line 1638 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetPressure(), GetVelocityVector(), Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_spacedim, Vmath::Vadd(), Vmath::Vcopy(), Vmath::Vmul(), and Vmath::Zero().

Referenced by v_InitObject().

1641  {
1642  int i, j;
1643  int nq = physfield[0].num_elements();
1644  int nVariables = m_fields.num_elements();
1645 
1646  Array<OneD, NekDouble> pressure(nq);
1647  Array<OneD, Array<OneD, NekDouble> > velocity(m_spacedim);
1648 
1649  // Flux vector for the rho equation
1650  for (i = 0; i < m_spacedim; ++i)
1651  {
1652  velocity[i] = Array<OneD, NekDouble>(nq);
1653  Vmath::Vcopy(nq, physfield[i+1], 1, flux[0][i], 1);
1654  }
1655 
1656  GetVelocityVector(physfield, velocity);
1657  GetPressure (physfield, velocity, pressure);
1658 
1659  // Flux vector for the velocity fields
1660  for (i = 0; i < m_spacedim; ++i)
1661  {
1662  for (j = 0; j < m_spacedim; ++j)
1663  {
1664  Vmath::Vmul(nq, velocity[j], 1, physfield[i+1], 1,
1665  flux[i+1][j], 1);
1666  }
1667 
1668  // Add pressure to appropriate field
1669  Vmath::Vadd(nq, flux[i+1][i], 1, pressure, 1, flux[i+1][i], 1);
1670  }
1671 
1672  // Flux vector for energy.
1673  Vmath::Vadd(nq, physfield[m_spacedim+1], 1, pressure, 1,
1674  pressure, 1);
1675 
1676  for (j = 0; j < m_spacedim; ++j)
1677  {
1678  Vmath::Vmul(nq, velocity[j], 1, pressure, 1,
1679  flux[m_spacedim+1][j], 1);
1680  }
1681 
1682  // For the smooth viscosity model
1683  if (nVariables == m_spacedim+3)
1684  {
1685  // Add a zero row for the advective fluxes
1686  for (j = 0; j < m_spacedim; ++j)
1687  {
1688  Vmath::Zero(nq, flux[m_spacedim+2][j], 1);
1689  }
1690  }
1691  }
Nektar::CompressibleFlowSystem::GetVelocityVector
void GetVelocityVector(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &velocity)
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::GetPressure
SOLVER_UTILS_EXPORT MultiRegions::ExpListSharedPtr GetPressure()
Get pressure field if available.
Definition: EquationSystem.h:750
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::GetFluxVectorDeAlias ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  flux 
)
protected

Return the flux vector for the compressible Euler equations by using the de-aliasing technique.

Parameters
iComponent of the flux vector to calculate.
physfieldFields.
fluxResulting flux.

Definition at line 1701 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetPressure(), GetVelocityVector(), Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_spacedim, Vmath::Vadd(), and Vmath::Vmul().

Referenced by v_InitObject().

1704  {
1705  int i, j;
1706  int nq = physfield[0].num_elements();
1707  int nVariables = m_fields.num_elements();
1708 
1709  // Factor to rescale 1d points in dealiasing
1710  NekDouble OneDptscale = 2;
1711  nq = m_fields[0]->Get1DScaledTotPoints(OneDptscale);
1712 
1713  Array<OneD, NekDouble> pressure(nq);
1714  Array<OneD, Array<OneD, NekDouble> > velocity(m_spacedim);
1715 
1716  Array<OneD, Array<OneD, NekDouble> > physfield_interp(nVariables);
1717  Array<OneD, Array<OneD, Array<OneD, NekDouble> > > flux_interp(
1718  nVariables);
1719 
1720  for (i = 0; i < nVariables; ++ i)
1721  {
1722  physfield_interp[i] = Array<OneD, NekDouble>(nq);
1723  flux_interp[i] = Array<OneD, Array<OneD, NekDouble> >(m_spacedim);
1724  m_fields[0]->PhysInterp1DScaled(
1725  OneDptscale, physfield[i], physfield_interp[i]);
1726 
1727  for (j = 0; j < m_spacedim; ++j)
1728  {
1729  flux_interp[i][j] = Array<OneD, NekDouble>(nq);
1730  }
1731  }
1732 
1733  // Flux vector for the rho equation
1734  for (i = 0; i < m_spacedim; ++i)
1735  {
1736  velocity[i] = Array<OneD, NekDouble>(nq);
1737 
1738  // Galerkin project solution back to original space
1739  m_fields[0]->PhysGalerkinProjection1DScaled(
1740  OneDptscale, physfield_interp[i+1], flux[0][i]);
1741  }
1742 
1743  GetVelocityVector(physfield_interp, velocity);
1744  GetPressure (physfield_interp, velocity, pressure);
1745 
1746  // Evaluation of flux vector for the velocity fields
1747  for (i = 0; i < m_spacedim; ++i)
1748  {
1749  for (j = 0; j < m_spacedim; ++j)
1750  {
1751  Vmath::Vmul(nq, velocity[j], 1, physfield_interp[i+1], 1,
1752  flux_interp[i+1][j], 1);
1753  }
1754 
1755  // Add pressure to appropriate field
1756  Vmath::Vadd(nq, flux_interp[i+1][i], 1, pressure,1,
1757  flux_interp[i+1][i], 1);
1758  }
1759 
1760  // Galerkin project solution back to origianl space
1761  for (i = 0; i < m_spacedim; ++i)
1762  {
1763  for (j = 0; j < m_spacedim; ++j)
1764  {
1765  m_fields[0]->PhysGalerkinProjection1DScaled(
1766  OneDptscale, flux_interp[i+1][j], flux[i+1][j]);
1767  }
1768  }
1769 
1770  // Evaluation of flux vector for energy
1771  Vmath::Vadd(nq, physfield_interp[m_spacedim+1], 1, pressure, 1,
1772  pressure, 1);
1773 
1774  for (j = 0; j < m_spacedim; ++j)
1775  {
1776  Vmath::Vmul(nq, velocity[j], 1, pressure, 1,
1777  flux_interp[m_spacedim+1][j], 1);
1778 
1779  // Galerkin project solution back to origianl space
1780  m_fields[0]->PhysGalerkinProjection1DScaled(
1781  OneDptscale,
1782  flux_interp[m_spacedim+1][j],
1783  flux[m_spacedim+1][j]);
1784  }
1785  }
Nektar::CompressibleFlowSystem::GetVelocityVector
void GetVelocityVector(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, NekDouble > > &velocity)
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::GetPressure
SOLVER_UTILS_EXPORT MultiRegions::ExpListSharedPtr GetPressure()
Get pressure field if available.
Definition: EquationSystem.h:750
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::GetFluxVectorPDESC ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  flux 
)
protected
void Nektar::CompressibleFlowSystem::GetForcingTerm ( const Array< OneD, const Array< OneD, NekDouble > > &  inarray,
Array< OneD, Array< OneD, NekDouble > >  outarrayForcing 
)
protected

Referenced by Nektar::EulerADCFE::DoOdeRhs().

NekDouble Nektar::CompressibleFlowSystem::GetGamma ( )
inlineprotected

Definition at line 280 of file CompressibleFlowSystem.h.

References m_gamma.

Referenced by v_InitObject().

281  {
282  return m_gamma;
283  }
NekDouble Nektar::CompressibleFlowSystem::GetGasConstant ( )
inlineprotected

Definition at line 275 of file CompressibleFlowSystem.h.

References m_gasConstant.

276  {
277  return m_gasConstant;
278  }
void Nektar::CompressibleFlowSystem::GetMach ( Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  soundspeed,
Array< OneD, NekDouble > &  mach 
)
protected
const Array<OneD, const Array<OneD, NekDouble> >& Nektar::CompressibleFlowSystem::GetNormals ( )
inlineprotected

Definition at line 290 of file CompressibleFlowSystem.h.

References Nektar::SolverUtils::EquationSystem::m_traceNormals.

Referenced by v_InitObject().

291  {
292  return m_traceNormals;
293  }
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
void Nektar::CompressibleFlowSystem::GetPressure ( const Array< OneD, const Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  pressure 
)
protected

Calculate the pressure field 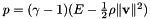$ p = (\gamma-1)(E-\frac{1}{2}\rho\| \mathbf{v} \|^2) $ assuming an ideal gas law.

Parameters
physfieldInput momentum.
pressureComputed pressure field.

Definition at line 2550 of file CompressibleFlowSystem.cpp.

References m_gamma, Nektar::SolverUtils::EquationSystem::m_spacedim, Vmath::Smul(), Vmath::Svtvp(), Vmath::Vdiv(), Vmath::Vmul(), and Vmath::Vvtvp().

2553  {
2554  int nBCEdgePts = physfield[0].num_elements();
2555  NekDouble alpha = -0.5;
2556 
2557  // Calculate ||rho v||^2
2558  Vmath::Vmul(nBCEdgePts, physfield[1], 1, physfield[1], 1, pressure, 1);
2559  for (int i = 1; i < m_spacedim; ++i)
2560  {
2561  Vmath::Vvtvp(nBCEdgePts, physfield[1+i], 1, physfield[1+i], 1,
2562  pressure, 1, pressure, 1);
2563  }
2564  // Divide by rho to get rho*||v||^2
2565  Vmath::Vdiv (nBCEdgePts, pressure, 1, physfield[0], 1, pressure, 1);
2566  // pressure <- E - 0.5*pressure
2567  Vmath::Svtvp(nBCEdgePts, alpha,
2568  pressure, 1, physfield[m_spacedim+1], 1, pressure, 1);
2569  // Multiply by (gamma-1)
2570  Vmath::Smul (nBCEdgePts, m_gamma-1, pressure, 1, pressure, 1);
2571  }
Vmath::Svtvp
void Svtvp(int n, const T alpha, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
svtvp (scalar times vector plus vector): z = alpha*x + y
Definition: Vmath.cpp:471
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::GetPressure ( const Array< OneD, const Array< OneD, NekDouble > > &  physfield,
const Array< OneD, const Array< OneD, NekDouble > > &  velocity,
Array< OneD, NekDouble > &  pressure 
)
protected
void Nektar::CompressibleFlowSystem::GetSensor ( const Array< OneD, const Array< OneD, NekDouble > > &  physarray,
Array< OneD, NekDouble > &  Sensor,
Array< OneD, NekDouble > &  SensorKappa 
)
protected
void Nektar::CompressibleFlowSystem::GetSmoothArtificialViscosity ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  eps_bar 
)
protected

Referenced by v_InitObject().

void Nektar::CompressibleFlowSystem::GetSoundSpeed ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  pressure,
Array< OneD, NekDouble > &  soundspeed 
)
protected

Referenced by Nektar::EulerADCFE::DoOdeRhs().

NekDouble Nektar::CompressibleFlowSystem::GetStabilityLimit ( int  n)

Function to calculate the stability limit for DG/CG.

Array<OneD, NekDouble> Nektar::CompressibleFlowSystem::GetStabilityLimitVector ( const Array< OneD, int > &  ExpOrder)

Function to calculate the stability limit for DG/CG (a vector of them).

void Nektar::CompressibleFlowSystem::GetStdVelocity ( const Array< OneD, const Array< OneD, NekDouble > > &  inarray,
Array< OneD, NekDouble > &  stdV 
)
protected
void Nektar::CompressibleFlowSystem::GetTemperature ( const Array< OneD, const Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  pressure,
Array< OneD, NekDouble > &  temperature 
)
protected

Referenced by Nektar::NavierStokesCFE::DoOdeRhs(), and GetViscousFluxVectorDeAlias().

const Array<OneD, const Array<OneD, NekDouble> >& Nektar::CompressibleFlowSystem::GetVecLocs ( )
inlineprotected

Definition at line 285 of file CompressibleFlowSystem.h.

References m_vecLocs.

Referenced by v_InitObject().

286  {
287  return m_vecLocs;
288  }
Nektar::CompressibleFlowSystem::m_vecLocs
Array< OneD, Array< OneD, NekDouble > > m_vecLocs
Definition: CompressibleFlowSystem.h:83
void Nektar::CompressibleFlowSystem::GetVelocityVector ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, Array< OneD, NekDouble > > &  velocity 
)
protected

Referenced by GetFluxVector(), and GetFluxVectorDeAlias().

void Nektar::CompressibleFlowSystem::GetViscousFluxVector ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  derivativesO1,
Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  viscousTensor 
)
protected

Return the flux vector for the LDG diffusion problem.

Todo:
Complete the viscous flux vector

Definition at line 1792 of file CompressibleFlowSystem.cpp.

References ASSERTL0, Vmath::Fill(), GetDynamicViscosity(), m_Cp, Nektar::SolverUtils::EquationSystem::m_fields, m_mu, m_Prandtl, Nektar::SolverUtils::EquationSystem::m_spacedim, m_thermalConductivity, m_ViscosityType, Vmath::Smul(), Vmath::Vadd(), Vmath::Vcopy(), Vmath::Vmul(), and Vmath::Zero().

Referenced by v_InitObject().

1796  {
1797  int j, k;
1798  int nVariables = m_fields.num_elements();
1799  int nPts = physfield[0].num_elements();
1800 
1801  // Stokes hypotesis
1802  const NekDouble lambda = -2.0/3.0;
1803 
1804  // Auxiliary variables
1805  Array<OneD, NekDouble > mu (nPts, 0.0);
1806  Array<OneD, NekDouble > thermalConductivity(nPts, 0.0);
1807  Array<OneD, NekDouble > mu2 (nPts, 0.0);
1808  Array<OneD, NekDouble > divVel (nPts, 0.0);
1809 
1810  // Variable viscosity through the Sutherland's law
1811  if (m_ViscosityType == "Variable")
1812  {
1813  GetDynamicViscosity(physfield[nVariables-2], mu);
1814  NekDouble tRa = m_Cp / m_Prandtl;
1815  Vmath::Smul(nPts, tRa, &mu[0], 1, &thermalConductivity[0], 1);
1816  }
1817  else
1818  {
1819  Vmath::Fill(nPts, m_mu, &mu[0], 1);
1820  Vmath::Fill(nPts, m_thermalConductivity,
1821  &thermalConductivity[0], 1);
1822  }
1823 
1824  // Computing diagonal terms of viscous stress tensor
1825  Array<OneD, Array<OneD, NekDouble> > tmp(m_spacedim);
1826  Array<OneD, Array<OneD, NekDouble> > Sgg(m_spacedim);
1827 
1828  // mu2 = 2 * mu
1829  Vmath::Smul(nPts, 2.0, &mu[0], 1, &mu2[0], 1);
1830 
1831  // Velocity divergence
1832  for (j = 0; j < m_spacedim; ++j)
1833  {
1834  Vmath::Vadd(nPts, &divVel[0], 1, &derivativesO1[j][j][0], 1,
1835  &divVel[0], 1);
1836  }
1837 
1838  // Velocity divergence scaled by lambda * mu
1839  Vmath::Smul(nPts, lambda, &divVel[0], 1, &divVel[0], 1);
1840  Vmath::Vmul(nPts, &mu[0], 1, &divVel[0], 1, &divVel[0], 1);
1841 
1842  // Diagonal terms of viscous stress tensor (Sxx, Syy, Szz)
1843  // Sjj = 2 * mu * du_j/dx_j - (2 / 3) * mu * sum_j(du_j/dx_j)
1844  for (j = 0; j < m_spacedim; ++j)
1845  {
1846  tmp[j] = Array<OneD, NekDouble>(nPts, 0.0);
1847  Sgg[j] = Array<OneD, NekDouble>(nPts, 0.0);
1848 
1849  Vmath::Vmul(nPts, &mu2[0], 1, &derivativesO1[j][j][0], 1,
1850  &tmp[j][0], 1);
1851 
1852  Vmath::Vadd(nPts, &tmp[j][0], 1, &divVel[0], 1, &Sgg[j][0], 1);
1853  }
1854 
1855  // Extra diagonal terms of viscous stress tensor (Sxy, Sxz, Syz)
1856  // Note: they exist for 2D and 3D problems only
1857  Array<OneD, NekDouble > Sxy(nPts, 0.0);
1858  Array<OneD, NekDouble > Sxz(nPts, 0.0);
1859  Array<OneD, NekDouble > Syz(nPts, 0.0);
1860 
1861  if (m_spacedim == 2)
1862  {
1863  // Sxy = (du/dy + dv/dx)
1864  Vmath::Vadd(nPts, &derivativesO1[0][1][0], 1,
1865  &derivativesO1[1][0][0], 1, &Sxy[0], 1);
1866 
1867  // Sxy = mu * (du/dy + dv/dx)
1868  Vmath::Vmul(nPts, &mu[0], 1, &Sxy[0], 1, &Sxy[0], 1);
1869  }
1870  else if (m_spacedim == 3)
1871  {
1872  // Sxy = (du/dy + dv/dx)
1873  Vmath::Vadd(nPts, &derivativesO1[0][1][0], 1,
1874  &derivativesO1[1][0][0], 1, &Sxy[0], 1);
1875 
1876  // Sxz = (du/dz + dw/dx)
1877  Vmath::Vadd(nPts, &derivativesO1[0][2][0], 1,
1878  &derivativesO1[2][0][0], 1, &Sxz[0], 1);
1879 
1880  // Syz = (dv/dz + dw/dy)
1881  Vmath::Vadd(nPts, &derivativesO1[1][2][0], 1,
1882  &derivativesO1[2][1][0], 1, &Syz[0], 1);
1883 
1884  // Sxy = mu * (du/dy + dv/dx)
1885  Vmath::Vmul(nPts, &mu[0], 1, &Sxy[0], 1, &Sxy[0], 1);
1886 
1887  // Sxz = mu * (du/dy + dv/dx)
1888  Vmath::Vmul(nPts, &mu[0], 1, &Sxz[0], 1, &Sxz[0], 1);
1889 
1890  // Syz = mu * (du/dy + dv/dx)
1891  Vmath::Vmul(nPts, &mu[0], 1, &Syz[0], 1, &Syz[0], 1);
1892  }
1893 
1894  // Energy-related terms
1895  Array<OneD, NekDouble > STx(nPts, 0.0);
1896  Array<OneD, NekDouble > STy(nPts, 0.0);
1897  Array<OneD, NekDouble > STz(nPts, 0.0);
1898 
1899  // Building the viscous flux vector
1900 
1901  // Viscous flux vector for the rho equation
1902  for (k = 0; k < m_spacedim; ++k)
1903  {
1904  Vmath::Zero(nPts, viscousTensor[k][0], 1);
1905  }
1906 
1907  if (m_spacedim == 1)
1908  {
1909  Array<OneD, NekDouble > tmp1(nPts, 0.0);
1910 
1911  // u * Sxx
1912  Vmath::Vmul(nPts, &physfield[0][0], 1, &Sgg[0][0], 1, &STx[0], 1);
1913 
1914  // k * dT/dx
1915  Vmath::Vmul(nPts, &thermalConductivity[0], 1,
1916  &derivativesO1[0][1][0], 1, &tmp1[0], 1);
1917 
1918  // STx = u * Sxx + (K / mu) * dT/dx
1919  Vmath::Vadd(nPts, &STx[0], 1, &tmp1[0], 1, &STx[0], 1);
1920  }
1921  else if (m_spacedim == 2)
1922  {
1923  Array<OneD, NekDouble > tmp1(nPts, 0.0);
1924  Array<OneD, NekDouble > tmp2(nPts, 0.0);
1925 
1926  // Computation of STx
1927 
1928  // u * Sxx
1929  Vmath::Vmul(nPts, &physfield[0][0], 1, &Sgg[0][0], 1, &STx[0], 1);
1930 
1931  // v * Sxy
1932  Vmath::Vmul(nPts, &physfield[1][0], 1, &Sxy[0], 1, &tmp1[0], 1);
1933 
1934  // k * dT/dx
1935  Vmath::Vmul(nPts, &thermalConductivity[0], 1,
1936  &derivativesO1[0][2][0], 1, &tmp2[0], 1);
1937 
1938  // STx = u * Sxx + v * Sxy + K * dT/dx
1939  Vmath::Vadd(nPts, &STx[0], 1, &tmp1[0], 1, &STx[0], 1);
1940  Vmath::Vadd(nPts, &STx[0], 1, &tmp2[0], 1, &STx[0], 1);
1941 
1942  // Computation of STy
1943 
1944  // Re-initialise temporary arrays
1945  Vmath::Zero(nPts, &tmp1[0], 1);
1946  Vmath::Zero(nPts, &tmp2[0], 1);
1947 
1948  // v * Syy
1949  Vmath::Vmul(nPts, &physfield[1][0], 1, &Sgg[1][0], 1, &STy[0], 1);
1950 
1951  // u * Sxy
1952  Vmath::Vmul(nPts, &physfield[0][0], 1, &Sxy[0], 1, &tmp1[0], 1);
1953 
1954  // k * dT/dy
1955  Vmath::Vmul(nPts, &thermalConductivity[0], 1,
1956  &derivativesO1[1][2][0], 1, &tmp2[0], 1);
1957 
1958  // STy = v * Syy + u * Sxy + K * dT/dy
1959  Vmath::Vadd(nPts, &STy[0], 1, &tmp1[0], 1, &STy[0], 1);
1960  Vmath::Vadd(nPts, &STy[0], 1, &tmp2[0], 1, &STy[0], 1);
1961  }
1962  else if (m_spacedim == 3)
1963  {
1964  Array<OneD, NekDouble > tmp1(nPts, 0.0);
1965  Array<OneD, NekDouble > tmp2(nPts, 0.0);
1966  Array<OneD, NekDouble > tmp3(nPts, 0.0);
1967 
1968  // Computation of STx
1969 
1970  // u * Sxx
1971  Vmath::Vmul(nPts, &physfield[0][0], 1, &Sgg[0][0], 1, &STx[0], 1);
1972 
1973  // v * Sxy
1974  Vmath::Vmul(nPts, &physfield[1][0], 1, &Sxy[0], 1, &tmp1[0], 1);
1975 
1976  // v * Sxz
1977  Vmath::Vmul(nPts, &physfield[2][0], 1, &Sxz[0], 1, &tmp2[0], 1);
1978 
1979  // k * dT/dx
1980  Vmath::Vmul(nPts, &thermalConductivity[0], 1,
1981  &derivativesO1[0][3][0], 1, &tmp3[0], 1);
1982 
1983  // STx = u * Sxx + v * Sxy + w * Sxz + (K / mu) * dT/dx
1984  Vmath::Vadd(nPts, &STx[0], 1, &tmp1[0], 1, &STx[0], 1);
1985  Vmath::Vadd(nPts, &STx[0], 1, &tmp2[0], 1, &STx[0], 1);
1986  Vmath::Vadd(nPts, &STx[0], 1, &tmp3[0], 1, &STx[0], 1);
1987 
1988  // Computation of STy
1989 
1990  // Re-initialise temporary arrays
1991  Vmath::Zero(nPts, &tmp1[0], 1);
1992  Vmath::Zero(nPts, &tmp2[0], 1);
1993  Vmath::Zero(nPts, &tmp3[0], 1);
1994 
1995  // v * Syy
1996  Vmath::Vmul(nPts, &physfield[1][0], 1, &Sgg[1][0], 1, &STy[0], 1);
1997 
1998  // u * Sxy
1999  Vmath::Vmul(nPts, &physfield[0][0], 1, &Sxy[0], 1, &tmp1[0], 1);
2000 
2001  // w * Syz
2002  Vmath::Vmul(nPts, &physfield[2][0], 1, &Syz[0], 1, &tmp2[0], 1);
2003 
2004  // k * dT/dy
2005  Vmath::Vmul(nPts, &thermalConductivity[0], 1,
2006  &derivativesO1[1][3][0], 1, &tmp3[0], 1);
2007 
2008  // STy = v * Syy + u * Sxy + w * Syz + K * dT/dy
2009  Vmath::Vadd(nPts, &STy[0], 1, &tmp1[0], 1, &STy[0], 1);
2010  Vmath::Vadd(nPts, &STy[0], 1, &tmp2[0], 1, &STy[0], 1);
2011  Vmath::Vadd(nPts, &STy[0], 1, &tmp3[0], 1, &STy[0], 1);
2012 
2013  // Computation of STz
2014 
2015  // Re-initialise temporary arrays
2016  Vmath::Zero(nPts, &tmp1[0], 1);
2017  Vmath::Zero(nPts, &tmp2[0], 1);
2018  Vmath::Zero(nPts, &tmp3[0], 1);
2019 
2020  // w * Szz
2021  Vmath::Vmul(nPts, &physfield[2][0], 1, &Sgg[2][0], 1, &STz[0], 1);
2022 
2023  // u * Sxz
2024  Vmath::Vmul(nPts, &physfield[0][0], 1, &Sxz[0], 1, &tmp1[0], 1);
2025 
2026  // v * Syz
2027  Vmath::Vmul(nPts, &physfield[1][0], 1, &Syz[0], 1, &tmp2[0], 1);
2028 
2029  // k * dT/dz
2030  Vmath::Vmul(nPts, &thermalConductivity[0], 1,
2031  &derivativesO1[2][3][0], 1, &tmp3[0], 1);
2032 
2033  // STz = w * Szz + u * Sxz + v * Syz + K * dT/dz
2034  Vmath::Vadd(nPts, &STz[0], 1, &tmp1[0], 1, &STz[0], 1);
2035  Vmath::Vadd(nPts, &STz[0], 1, &tmp2[0], 1, &STz[0], 1);
2036  Vmath::Vadd(nPts, &STz[0], 1, &tmp3[0], 1, &STz[0], 1);
2037  }
2038 
2039  switch (m_spacedim)
2040  {
2041  case 1:
2042  {
2043  // f_11v = f_rho = 0
2044  Vmath::Zero(nPts, &viscousTensor[0][0][0], 1);
2045 
2046  // f_21v = f_rhou
2047  Vmath::Vcopy(nPts, &Sgg[0][0], 1, &viscousTensor[0][1][0], 1);
2048 
2049  // f_31v = f_E
2050  Vmath::Vcopy(nPts, &STx[0], 1, &viscousTensor[0][2][0], 1);
2051  break;
2052  }
2053  case 2:
2054  {
2055  // f_11v = f_rho1 = 0
2056  Vmath::Zero(nPts, &viscousTensor[0][0][0], 1);
2057  // f_12v = f_rho2 = 0
2058  Vmath::Zero(nPts, &viscousTensor[1][0][0], 1);
2059 
2060  // f_21v = f_rhou1
2061  Vmath::Vcopy(nPts, &Sgg[0][0], 1, &viscousTensor[0][1][0], 1);
2062  // f_22v = f_rhou2
2063  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor[1][1][0], 1);
2064 
2065  // f_31v = f_rhov1
2066  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor[0][2][0], 1);
2067  // f_32v = f_rhov2
2068  Vmath::Vcopy(nPts, &Sgg[1][0], 1, &viscousTensor[1][2][0], 1);
2069 
2070  // f_41v = f_E1
2071  Vmath::Vcopy(nPts, &STx[0], 1, &viscousTensor[0][3][0], 1);
2072  // f_42v = f_E2
2073  Vmath::Vcopy(nPts, &STy[0], 1, &viscousTensor[1][3][0], 1);
2074  break;
2075  }
2076  case 3:
2077  {
2078  // f_11v = f_rho1 = 0
2079  Vmath::Zero(nPts, &viscousTensor[0][0][0], 1);
2080  // f_12v = f_rho2 = 0
2081  Vmath::Zero(nPts, &viscousTensor[1][0][0], 1);
2082  // f_13v = f_rho3 = 0
2083  Vmath::Zero(nPts, &viscousTensor[2][0][0], 1);
2084 
2085  // f_21v = f_rhou1
2086  Vmath::Vcopy(nPts, &Sgg[0][0], 1, &viscousTensor[0][1][0], 1);
2087  // f_22v = f_rhou2
2088  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor[1][1][0], 1);
2089  // f_23v = f_rhou3
2090  Vmath::Vcopy(nPts, &Sxz[0], 1, &viscousTensor[2][1][0], 1);
2091 
2092  // f_31v = f_rhov1
2093  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor[0][2][0], 1);
2094  // f_32v = f_rhov2
2095  Vmath::Vcopy(nPts, &Sgg[1][0], 1, &viscousTensor[1][2][0], 1);
2096  // f_33v = f_rhov3
2097  Vmath::Vcopy(nPts, &Syz[0], 1, &viscousTensor[2][2][0], 1);
2098 
2099  // f_31v = f_rhow1
2100  Vmath::Vcopy(nPts, &Sxz[0], 1, &viscousTensor[0][3][0], 1);
2101  // f_32v = f_rhow2
2102  Vmath::Vcopy(nPts, &Syz[0], 1, &viscousTensor[1][3][0], 1);
2103  // f_33v = f_rhow3
2104  Vmath::Vcopy(nPts, &Sgg[2][0], 1, &viscousTensor[2][3][0], 1);
2105 
2106  // f_41v = f_E1
2107  Vmath::Vcopy(nPts, &STx[0], 1, &viscousTensor[0][4][0], 1);
2108  // f_42v = f_E2
2109  Vmath::Vcopy(nPts, &STy[0], 1, &viscousTensor[1][4][0], 1);
2110  // f_43v = f_E3
2111  Vmath::Vcopy(nPts, &STz[0], 1, &viscousTensor[2][4][0], 1);
2112  break;
2113  }
2114  default:
2115  {
2116  ASSERTL0(false, "Illegal expansion dimension");
2117  }
2118  }
2119  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Vmath::Fill
void Fill(int n, const T alpha, T *x, const int incx)
Fill a vector with a constant value.
Definition: Vmath.cpp:46
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::CompressibleFlowSystem::GetDynamicViscosity
void GetDynamicViscosity(const Array< OneD, const NekDouble > &temperature, Array< OneD, NekDouble > &mu)
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::GetViscousFluxVectorDeAlias ( const Array< OneD, Array< OneD, NekDouble > > &  physfield,
Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  derivativesO1,
Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &  viscousTensor 
)
protected

Return the flux vector for the LDG diffusion problem.

Todo:
Complete the viscous flux vector

Definition at line 2125 of file CompressibleFlowSystem.cpp.

References ASSERTL0, GetDynamicViscosity(), Nektar::SolverUtils::EquationSystem::GetPressure(), GetTemperature(), Nektar::SolverUtils::EquationSystem::m_fields, m_mu, Nektar::SolverUtils::EquationSystem::m_spacedim, m_thermalConductivity, m_ViscosityType, Vmath::Sadd(), Vmath::Smul(), Vmath::Vadd(), Vmath::Vcopy(), Vmath::Vmul(), and Vmath::Zero().

Referenced by v_InitObject().

2129  {
2130 #if 0
2131  int i, j, k;
2132  int nVariables = m_fields.num_elements();
2133  int nPts = physfield[0].num_elements();
2134 
2135  int variables_phys = physfield.num_elements();
2136 
2137  // Factor to rescale 1d points in dealiasing.
2138  NekDouble OneDptscale = 2;
2139 
2140  // Get number of points to dealias a cubic non-linearity
2141  nPts = m_fields[0]->Get1DScaledTotPoints(OneDptscale);
2142 
2143  int nVariables_aux = derivativesO1[0].num_elements();
2144 
2145  Array<OneD, Array<OneD, NekDouble> > physfield_interp(variables_phys);
2146  Array<OneD, Array<OneD, Array<OneD, NekDouble> > > derivativesO1_interp(
2147  m_spacedim);
2148  Array<OneD, Array<OneD, Array<OneD, NekDouble> > >viscousTensor_interp(
2149  m_spacedim);
2150 
2151  for (i = 0; i < m_spacedim; ++ i)
2152  {
2153  viscousTensor_interp[i] = Array<OneD, Array<OneD, NekDouble> >(
2154  nVariables);
2155  for (j = 0; j < nVariables; ++j)
2156  {
2157  viscousTensor_interp[i][j] = Array<OneD, NekDouble>(nPts);
2158  }
2159  }
2160 
2161  // Stokes hypotesis
2162  NekDouble lambda = -2.0/3.0;
2163 
2164  // Auxiliary variables
2165  Array<OneD, NekDouble > mu (nPts, 0.0);
2166  Array<OneD, NekDouble > mu2 (nPts, 0.0);
2167  Array<OneD, NekDouble > divVel (nPts, 0.0);
2168  Array<OneD, NekDouble > pressure (nPts, 0.0);
2169  Array<OneD, NekDouble > temperature(nPts, 0.0);
2170 
2171  for (i = 0; i < nVariables; ++i)
2172  {
2173  m_fields[0]->PhysInterp1DScaled(
2174  OneDptscale, physfield[i], fields_interp[i]);
2175  }
2176 
2177  for (i = 0; i < variables_phys; ++i)
2178  {
2179  physfield_interp[i] = Array<OneD, NekDouble> (nPts);
2180 
2181  // Interpolation to higher space
2182  m_fields[0]->PhysInterp1DScaled(OneDptscale, physfield[i],
2183  physfield_interp[i]);
2184  }
2185 
2186  for (i = 0; i < m_spacedim; ++i)
2187  {
2188  derivativesO1_interp[i] = Array<OneD, Array<OneD, NekDouble> >(
2189  nVariables_aux);
2190  for (j = 0; j < nVariables_aux; ++j)
2191  {
2192  derivativesO1_interp[i][j] = Array<OneD, NekDouble>(nPts);
2193  m_fields[0]->PhysInterp1DScaled(
2194  OneDptscale, derivativesO1[i][j],
2195  derivativesO1_interp[i][j]);
2196  }
2197  }
2198 
2199  // Thermodynamic related quantities
2200  GetPressure(fields_interp, pressure);
2201  GetTemperature(fields_interp, pressure, temperature);
2202 
2203  // Variable viscosity through the Sutherland's law
2204  if (m_ViscosityType == "Variable")
2205  {
2206  GetDynamicViscosity(fields_interp[variables_phys-1], mu);
2207  }
2208  else
2209  {
2210  Vmath::Sadd(nPts, m_mu, &mu[0], 1, &mu[0], 1);
2211  }
2212 
2213  // Computing diagonal terms of viscous stress tensor
2214  Array<OneD, Array<OneD, NekDouble> > tmp(m_spacedim);
2215  Array<OneD, Array<OneD, NekDouble> > Sgg(m_spacedim);
2216 
2217  // mu2 = 2 * mu
2218  Vmath::Smul(nPts, 2.0, &mu[0], 1, &mu2[0], 1);
2219 
2220  // Velocity divergence
2221  for (j = 0; j < m_spacedim; ++j)
2222  {
2223  Vmath::Vadd(nPts, &divVel[0], 1, &derivativesO1_interp[j][j][0], 1,
2224  &divVel[0], 1);
2225  }
2226 
2227  // Velocity divergence scaled by lambda * mu
2228  Vmath::Smul(nPts, lambda, &divVel[0], 1, &divVel[0], 1);
2229  Vmath::Vmul(nPts, &mu[0], 1, &divVel[0], 1, &divVel[0], 1);
2230 
2231  // Digonal terms of viscous stress tensor (Sxx, Syy, Szz)
2232  // Sjj = 2 * mu * du_j/dx_j - (2 / 3) * mu * sum_j(du_j/dx_j)
2233  for (j = 0; j < m_spacedim; ++j)
2234  {
2235  tmp[j] = Array<OneD, NekDouble>(nPts, 0.0);
2236  Sgg[j] = Array<OneD, NekDouble>(nPts, 0.0);
2237 
2238  Vmath::Vmul(nPts, &mu2[0], 1, &derivativesO1_interp[j][j][0], 1,
2239  &tmp[j][0], 1);
2240 
2241  Vmath::Vadd(nPts, &tmp[j][0], 1, &divVel[0], 1, &Sgg[j][0], 1);
2242  }
2243 
2244  // Extra diagonal terms of viscous stress tensor (Sxy, Sxz, Syz)
2245  // Note: they exist for 2D and 3D problems only
2246  Array<OneD, NekDouble > Sxy(nPts, 0.0);
2247  Array<OneD, NekDouble > Sxz(nPts, 0.0);
2248  Array<OneD, NekDouble > Syz(nPts, 0.0);
2249 
2250  if (m_spacedim == 2)
2251  {
2252  // Sxy = (du/dy + dv/dx)
2253  Vmath::Vadd(nPts, &derivativesO1_interp[0][1][0], 1,
2254  &derivativesO1_interp[1][0][0], 1, &Sxy[0], 1);
2255 
2256  // Sxy = mu * (du/dy + dv/dx)
2257  Vmath::Vmul(nPts, &mu[0], 1, &Sxy[0], 1, &Sxy[0], 1);
2258  }
2259  else if (m_spacedim == 3)
2260  {
2261  // Sxy = (du/dy + dv/dx)
2262  Vmath::Vadd(nPts, &derivativesO1_interp[0][1][0], 1,
2263  &derivativesO1_interp[1][0][0], 1, &Sxy[0], 1);
2264 
2265  // Sxz = (du/dz + dw/dx)
2266  Vmath::Vadd(nPts, &derivativesO1_interp[0][2][0], 1,
2267  &derivativesO1_interp[2][0][0], 1, &Sxz[0], 1);
2268 
2269  // Syz = (dv/dz + dw/dy)
2270  Vmath::Vadd(nPts, &derivativesO1_interp[1][2][0], 1,
2271  &derivativesO1_interp[2][1][0], 1, &Syz[0], 1);
2272 
2273  // Sxy = mu * (du/dy + dv/dx)
2274  Vmath::Vmul(nPts, &mu[0], 1, &Sxy[0], 1, &Sxy[0], 1);
2275 
2276  // Sxz = mu * (du/dy + dv/dx)
2277  Vmath::Vmul(nPts, &mu[0], 1, &Sxz[0], 1, &Sxz[0], 1);
2278 
2279  // Syz = mu * (du/dy + dv/dx)
2280  Vmath::Vmul(nPts, &mu[0], 1, &Syz[0], 1, &Syz[0], 1);
2281  }
2282 
2283  // Energy-related terms
2284  Array<OneD, NekDouble > STx(nPts, 0.0);
2285  Array<OneD, NekDouble > STy(nPts, 0.0);
2286  Array<OneD, NekDouble > STz(nPts, 0.0);
2287  // Building the viscous flux vector
2288  if (i == 0)
2289  {
2290  // Viscous flux vector for the rho equation
2291  for (k = 0; k < m_spacedim; ++k)
2292  {
2293  Vmath::Zero(nPts, viscousTensor_interp[k][i], 1);
2294  }
2295  }
2296 
2297  if (m_spacedim == 1)
2298  {
2299  Array<OneD, NekDouble > tmp1(nPts, 0.0);
2300 
2301  // u * Sxx
2302  Vmath::Vmul(nPts, &physfield_interp[0][0], 1,
2303  &Sgg[0][0], 1, &STx[0], 1);
2304 
2305  // k * dT/dx
2306  Vmath::Smul(nPts, m_thermalConductivity,
2307  &derivativesO1_interp[0][1][0], 1, &tmp1[0], 1);
2308 
2309  // STx = u * Sxx + (K / mu) * dT/dx
2310  Vmath::Vadd(nPts, &STx[0], 1, &tmp1[0], 1, &STx[0], 1);
2311  }
2312  else if (m_spacedim == 2)
2313  {
2314  Array<OneD, NekDouble > tmp1(nPts, 0.0);
2315  Array<OneD, NekDouble > tmp2(nPts, 0.0);
2316 
2317  // Computation of STx
2318 
2319  // u * Sxx
2320  Vmath::Vmul(nPts, &physfield_interp[0][0], 1,
2321  &Sgg[0][0], 1, &STx[0], 1);
2322 
2323  // v * Sxy
2324  Vmath::Vmul(nPts, &physfield_interp[1][0], 1,
2325  &Sxy[0], 1, &tmp1[0], 1);
2326 
2327  // k * dT/dx
2328  Vmath::Smul(nPts, m_thermalConductivity,
2329  &derivativesO1_interp[0][2][0], 1, &tmp2[0], 1);
2330 
2331  // STx = u * Sxx + v * Sxy + K * dT/dx
2332  Vmath::Vadd(nPts, &STx[0], 1, &tmp1[0], 1, &STx[0], 1);
2333  Vmath::Vadd(nPts, &STx[0], 1, &tmp2[0], 1, &STx[0], 1);
2334 
2335  // Computation of STy
2336 
2337  // Re-initialise temporary arrays
2338  Vmath::Zero(nPts, &tmp1[0], 1);
2339  Vmath::Zero(nPts, &tmp2[0], 1);
2340 
2341  // v * Syy
2342  Vmath::Vmul(nPts, &physfield_interp[1][0], 1,
2343  &Sgg[1][0], 1, &STy[0], 1);
2344 
2345  // u * Sxy
2346  Vmath::Vmul(nPts, &physfield_interp[0][0], 1,
2347  &Sxy[0], 1, &tmp1[0], 1);
2348 
2349  // k * dT/dy
2350  Vmath::Smul(nPts, m_thermalConductivity,
2351  &derivativesO1_interp[1][2][0], 1, &tmp2[0], 1);
2352 
2353  // STy = v * Syy + u * Sxy + K * dT/dy
2354  Vmath::Vadd(nPts, &STy[0], 1, &tmp1[0], 1, &STy[0], 1);
2355  Vmath::Vadd(nPts, &STy[0], 1, &tmp2[0], 1, &STy[0], 1);
2356  }
2357  else if (m_spacedim == 3)
2358  {
2359  Array<OneD, NekDouble > tmp1(nPts, 0.0);
2360  Array<OneD, NekDouble > tmp2(nPts, 0.0);
2361  Array<OneD, NekDouble > tmp3(nPts, 0.0);
2362 
2363  // Computation of STx
2364 
2365  // u * Sxx
2366  Vmath::Vmul(nPts, &physfield_interp[0][0], 1,
2367  &Sgg[0][0], 1, &STx[0], 1);
2368 
2369  // v * Sxy
2370  Vmath::Vmul(nPts, &physfield_interp[1][0], 1,
2371  &Sxy[0], 1, &tmp1[0], 1);
2372 
2373  // v * Sxy
2374  Vmath::Vmul(nPts, &physfield_interp[2][0], 1,
2375  &Sxz[0], 1, &tmp2[0], 1);
2376 
2377  // k * dT/dx
2378  Vmath::Smul(nPts, m_thermalConductivity,
2379  &derivativesO1_interp[0][3][0], 1, &tmp3[0], 1);
2380 
2381  // STx = u * Sxx + v * Sxy + w * Sxz + (K / mu) * dT/dx
2382  Vmath::Vadd(nPts, &STx[0], 1, &tmp1[0], 1, &STx[0], 1);
2383  Vmath::Vadd(nPts, &STx[0], 1, &tmp2[0], 1, &STx[0], 1);
2384  Vmath::Vadd(nPts, &STx[0], 1, &tmp3[0], 1, &STx[0], 1);
2385 
2386  // Computation of STy
2387 
2388  // Re-initialise temporary arrays
2389  Vmath::Zero(nPts, &tmp1[0], 1);
2390  Vmath::Zero(nPts, &tmp2[0], 1);
2391  Vmath::Zero(nPts, &tmp3[0], 1);
2392 
2393  // v * Syy
2394  Vmath::Vmul(nPts, &physfield_interp[1][0], 1,
2395  &Sgg[1][0], 1, &STy[0], 1);
2396 
2397  // u * Sxy
2398  Vmath::Vmul(nPts, &physfield_interp[0][0], 1,
2399  &Sxy[0], 1, &tmp1[0], 1);
2400 
2401  // w * Syz
2402  Vmath::Vmul(nPts, &physfield_interp[2][0], 1,
2403  &Syz[0], 1, &tmp2[0], 1);
2404 
2405  // k * dT/dy
2406  Vmath::Smul(nPts, m_thermalConductivity,
2407  &derivativesO1_interp[1][3][0], 1, &tmp3[0], 1);
2408 
2409  // STy = v * Syy + u * Sxy + w * Syz + K * dT/dy
2410  Vmath::Vadd(nPts, &STy[0], 1, &tmp1[0], 1, &STy[0], 1);
2411  Vmath::Vadd(nPts, &STy[0], 1, &tmp2[0], 1, &STy[0], 1);
2412  Vmath::Vadd(nPts, &STy[0], 1, &tmp3[0], 1, &STy[0], 1);
2413 
2414  // Computation of STz
2415 
2416  // Re-initialise temporary arrays
2417  Vmath::Zero(nPts, &tmp1[0], 1);
2418  Vmath::Zero(nPts, &tmp2[0], 1);
2419  Vmath::Zero(nPts, &tmp3[0], 1);
2420 
2421  // w * Szz
2422  Vmath::Vmul(nPts, &physfield_interp[2][0], 1,
2423  &Sgg[2][0], 1, &STz[0], 1);
2424 
2425  // u * Sxz
2426  Vmath::Vmul(nPts, &physfield_interp[0][0], 1,
2427  &Sxz[0], 1, &tmp1[0], 1);
2428 
2429  // v * Syz
2430  Vmath::Vmul(nPts, &physfield_interp[1][0], 1,
2431  &Syz[0], 1, &tmp2[0], 1);
2432 
2433  // k * dT/dz
2434  Vmath::Smul(nPts, m_thermalConductivity,
2435  &derivativesO1_interp[2][3][0], 1, &tmp3[0], 1);
2436 
2437  // STz = w * Szz + u * Sxz + v * Syz + K * dT/dz
2438  Vmath::Vadd(nPts, &STz[0], 1, &tmp1[0], 1, &STz[0], 1);
2439  Vmath::Vadd(nPts, &STz[0], 1, &tmp2[0], 1, &STz[0], 1);
2440  Vmath::Vadd(nPts, &STz[0], 1, &tmp3[0], 1, &STz[0], 1);
2441  }
2442 
2443  switch (m_spacedim)
2444  {
2445  case 1:
2446  {
2447 
2448  int nq = physfield[0].num_elements();
2449  // f_11v = f_rho = 0
2450  Vmath::Zero(nq, &viscousTensor_interp[0][0][0], 1);
2451 
2452  // f_21v = f_rhou
2453  Vmath::Vcopy(nPts, &Sgg[0][0], 1, &viscousTensor_interp[0][1][0], 1);
2454 
2455  // f_31v = f_E
2456  Vmath::Vcopy(nPts, &STx[0], 1, &viscousTensor_interp[0][2][0], 1);
2457  break;
2458  }
2459  case 2:
2460  {
2461  int nq = physfield[0].num_elements();
2462  // f_11v = f_rho1 = 0
2463  Vmath::Zero(nq, &viscousTensor_interp[0][0][0], 1);
2464  // f_12v = f_rho2 = 0
2465  Vmath::Zero(nq, &viscousTensor_interp[1][0][0], 1);
2466 
2467  // f_21v = f_rhou1
2468  Vmath::Vcopy(nPts, &Sgg[0][0], 1, &viscousTensor_interp[0][1][0], 1);
2469  // f_22v = f_rhou2
2470  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor_interp[1][1][0], 1);
2471 
2472  // f_31v = f_rhov1
2473  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor_interp[0][2][0], 1);
2474  // f_32v = f_rhov2
2475  Vmath::Vcopy(nPts, &Sgg[1][0], 1, &viscousTensor_interp[1][2][0], 1);
2476 
2477  // f_41v = f_E1
2478  Vmath::Vcopy(nPts, &STx[0], 1, &viscousTensor_interp[0][3][0], 1);
2479  // f_42v = f_E2
2480  Vmath::Vcopy(nPts, &STy[0], 1, &viscousTensor_interp[1][3][0], 1);
2481  break;
2482  }
2483  case 3:
2484  {
2485  int nq = physfield[0].num_elements();
2486  // f_11v = f_rho1 = 0
2487  Vmath::Zero(nq, &viscousTensor_interp[0][0][0], 1);
2488  // f_12v = f_rho2 = 0
2489  Vmath::Zero(nq, &viscousTensor_interp[1][0][0], 1);
2490  // f_13v = f_rho3 = 0
2491  Vmath::Zero(nq, &viscousTensor_interp[2][0][0], 1);
2492 
2493  // f_21v = f_rhou1
2494  Vmath::Vcopy(nPts, &Sgg[0][0], 1, &viscousTensor_interp[0][1][0], 1);
2495  // f_22v = f_rhou2
2496  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor_interp[1][1][0], 1);
2497  // f_23v = f_rhou3
2498  Vmath::Vcopy(nPts, &Sxz[0], 1, &viscousTensor_interp[2][1][0], 1);
2499 
2500  // f_31v = f_rhov1
2501  Vmath::Vcopy(nPts, &Sxy[0], 1, &viscousTensor_interp[0][2][0], 1);
2502  // f_32v = f_rhov2
2503  Vmath::Vcopy(nPts, &Sgg[1][0], 1, &viscousTensor_interp[1][2][0], 1);
2504  // f_33v = f_rhov3
2505  Vmath::Vcopy(nPts, &Syz[0], 1, &viscousTensor_interp[2][2][0], 1);
2506 
2507  // f_31v = f_rhow1
2508  Vmath::Vcopy(nPts, &Sxz[0], 1, &viscousTensor_interp[0][3][0], 1);
2509  // f_32v = f_rhow2
2510  Vmath::Vcopy(nPts, &Syz[0], 1, &viscousTensor_interp[1][3][0], 1);
2511  // f_33v = f_rhow3
2512  Vmath::Vcopy(nPts, &Sgg[2][0], 1, &viscousTensor_interp[2][3][0], 1);
2513 
2514  // f_41v = f_E1
2515  Vmath::Vcopy(nPts, &STx[0], 1, &viscousTensor_interp[0][4][0], 1);
2516  // f_42v = f_E2
2517  Vmath::Vcopy(nPts, &STy[0], 1, &viscousTensor_interp[1][4][0], 1);
2518  // f_43v = f_E3
2519  Vmath::Vcopy(nPts, &STz[0], 1, &viscousTensor_interp[2][4][0], 1);
2520  break;
2521  }
2522  default:
2523  {
2524  ASSERTL0(false, "Illegal expansion dimension");
2525  }
2526  }
2527 
2528  for (i = 0; i < m_spacedim; ++i)
2529  {
2530  for (j = 1; j < nVariables; ++j)
2531  {
2532  // Galerkin project solution back to origianl space
2533  m_fields[0]->PhysGalerkinProjection1DScaled(
2534  OneDptscale,
2535  viscousTensor_interp[i][j],
2536  viscousTensor[i][j]);
2537  }
2538  }
2539 #endif
2540 }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::CompressibleFlowSystem::GetTemperature
void GetTemperature(const Array< OneD, const Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &pressure, Array< OneD, NekDouble > &temperature)
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Vmath::Sadd
void Sadd(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Add vector y = alpha + x.
Definition: Vmath.cpp:301
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::CompressibleFlowSystem::GetDynamicViscosity
void GetDynamicViscosity(const Array< OneD, const NekDouble > &temperature, Array< OneD, NekDouble > &mu)
Nektar::SolverUtils::EquationSystem::GetPressure
SOLVER_UTILS_EXPORT MultiRegions::ExpListSharedPtr GetPressure()
Get pressure field if available.
Definition: EquationSystem.h:750
Vmath::Zero
void Zero(int n, T *x, const int incx)
Zero vector.
Definition: Vmath.cpp:359
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::PressureInflowFileBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Pressure inflow boundary conditions for compressible flow problems where either the density and the velocities are assigned from a file or the full state is assigned from a file (depending on the problem type, either subsonic or supersonic).

Definition at line 1409 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetExpSize(), Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, m_fieldStorage, m_gamma, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_traceNormals, m_uInf, m_vInf, m_wInf, npts, Vmath::Smul(), Vmath::Vabs(), Vmath::Vadd(), Vmath::Vdiv(), Vmath::Vmul(), Vmath::Vsqrt(), and Vmath::Vvtvp().

Referenced by SetCommonBC().

1413  {
1414  int i, j;
1415  int nTracePts = GetTraceTotPoints();
1416  int nVariables = physarray.num_elements();
1417  int nDimensions = m_spacedim;
1418 
1419  const Array<OneD, const int> &traceBndMap
1420  = m_fields[0]->GetTraceBndMap();
1421 
1422  NekDouble gamma = m_gamma;
1423  NekDouble gammaMinusOne = gamma - 1.0;
1424  NekDouble gammaMinusOneInv = 1.0 / gammaMinusOne;
1425 
1426  Array<OneD, NekDouble> tmp1 (nTracePts, 0.0);
1427  Array<OneD, NekDouble> tmp2 (nTracePts, 0.0);
1428  Array<OneD, NekDouble> VnInf(nTracePts, 0.0);
1429  Array<OneD, NekDouble> velInf(nDimensions, 0.0);
1430 
1431  // Computing the normal velocity for characteristics coming
1432  // from outside the computational domain
1433  velInf[0] = m_uInf;
1434  Vmath::Smul(nTracePts, m_uInf, m_traceNormals[0], 1, VnInf, 1);
1435  if (nDimensions == 2 || nDimensions == 3)
1436  {
1437  velInf[1] = m_vInf;
1438  Vmath::Smul(nTracePts, m_vInf, m_traceNormals[1], 1, tmp1, 1);
1439  Vmath::Vadd(nTracePts, VnInf, 1, tmp1, 1, VnInf, 1);
1440  }
1441  if (nDimensions == 3)
1442  {
1443  velInf[2] = m_wInf;
1444  Vmath::Smul(nTracePts, m_wInf, m_traceNormals[2], 1, tmp2, 1);
1445  Vmath::Vadd(nTracePts, VnInf, 1, tmp2, 1, VnInf, 1);
1446  }
1447 
1448  // Get physical values of the forward trace
1449  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
1450 
1451  for (i = 0; i < nVariables; ++i)
1452  {
1453  Fwd[i] = Array<OneD, NekDouble>(nTracePts, 0.0);
1454  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
1455  }
1456 
1457  // Computing the normal velocity for characteristics coming
1458  // from inside the computational domain
1459  Array<OneD, NekDouble > Vn (nTracePts, 0.0);
1460  Array<OneD, NekDouble > Vel(nTracePts, 0.0);
1461  for (i = 0; i < nDimensions; ++i)
1462  {
1463  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, Vel, 1);
1464  Vmath::Vvtvp(nTracePts, m_traceNormals[i], 1, Vel, 1, Vn, 1, Vn, 1);
1465  }
1466 
1467  // Computing the absolute value of the velocity in order to compute the
1468  // Mach number to decide whether supersonic or subsonic
1469  Array<OneD, NekDouble > absVel(nTracePts, 0.0);
1470  for (i = 0; i < nDimensions; ++i)
1471  {
1472  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, tmp1, 1);
1473  Vmath::Vmul(nTracePts, tmp1, 1, tmp1, 1, tmp1, 1);
1474  Vmath::Vadd(nTracePts, tmp1, 1, absVel, 1, absVel, 1);
1475  }
1476  Vmath::Vsqrt(nTracePts, absVel, 1, absVel, 1);
1477 
1478  // Get speed of sound
1479  Array<OneD, NekDouble > soundSpeed (nTracePts, 0.0);
1480  Array<OneD, NekDouble > pressure (nTracePts, 0.0);
1481 
1482  for (i = 0; i < nTracePts; i++)
1483  {
1484  if (m_spacedim == 1)
1485  {
1486  pressure[i] = (gammaMinusOne) * (Fwd[2][i] -
1487  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i]));
1488  }
1489  else if (m_spacedim == 2)
1490  {
1491  pressure[i] = (gammaMinusOne) * (Fwd[3][i] -
1492  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1493  Fwd[2][i] * Fwd[2][i] / Fwd[0][i]));
1494  }
1495  else
1496  {
1497  pressure[i] = (gammaMinusOne) * (Fwd[4][i] -
1498  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1499  Fwd[2][i] * Fwd[2][i] / Fwd[0][i] +
1500  Fwd[3][i] * Fwd[3][i] / Fwd[0][i]));
1501  }
1502 
1503  soundSpeed[i] = sqrt(gamma * pressure[i] / Fwd[0][i]);
1504  }
1505 
1506  // Get Mach
1507  Array<OneD, NekDouble > Mach(nTracePts, 0.0);
1508  Vmath::Vdiv(nTracePts, Vn, 1, soundSpeed, 1, Mach, 1);
1509  Vmath::Vabs(nTracePts, Mach, 1, Mach, 1);
1510 
1511  // Auxiliary variables
1512  int e, id1, id2, npts, pnt;
1513  NekDouble rhoeb;
1514 
1515  // Loop on the bcRegions
1516  for (e = 0; e < m_fields[0]->GetBndCondExpansions()[bcRegion]->
1517  GetExpSize(); ++e)
1518  {
1519  npts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1520  GetExp(e)->GetTotPoints();
1521  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1522  GetPhys_Offset(e);
1523  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
1524 
1525  // Loop on points of bcRegion 'e'
1526  for (i = 0; i < npts; i++)
1527  {
1528  pnt = id2+i;
1529 
1530  // Subsonic flows
1531  if (Mach[pnt] < 0.99)
1532  {
1533  // Partial extrapolation for subsonic cases
1534  for (j = 0; j < nVariables-1; ++j)
1535  {
1536  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1537  UpdatePhys())[id1+i] = m_fieldStorage[j][id1+i];
1538  }
1539 
1540  // Kinetic energy calculation
1541  NekDouble Ek = 0.0;
1542  for (j = 1; j < nVariables-1; ++j)
1543  {
1544  Ek += 0.5 * (m_fieldStorage[j][id1+i] *
1545  m_fieldStorage[j][id1+i]) /
1546  m_fieldStorage[0][id1+i];
1547  }
1548  rhoeb = gammaMinusOneInv * pressure[pnt] + Ek;
1549 
1550  (m_fields[nVariables-1]->GetBndCondExpansions()[bcRegion]->
1551  UpdatePhys())[id1+i] = rhoeb;
1552  }
1553  // Supersonic flows
1554  else
1555  {
1556  for (j = 0; j < nVariables; ++j)
1557  {
1558  // Extrapolation for supersonic cases
1559  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1560  UpdatePhys())[id1+i] = Fwd[j][pnt];
1561  }
1562  }
1563  }
1564  }
1565  }
Nektar::CompressibleFlowSystem::m_fieldStorage
Array< OneD, Array< OneD, NekDouble > > m_fieldStorage
Definition: CompressibleFlowSystem.h:132
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Vmath::Vabs
void Vabs(int n, const T *x, const int incx, T *y, const int incy)
vabs: y = |x|
Definition: Vmath.cpp:410
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
npts
static std::string npts
Definition: InputFld.cpp:43
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::GetExpSize
SOLVER_UTILS_EXPORT int GetExpSize()
Definition: EquationSystem.h:853
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::PressureOutflowBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Pressure outflow boundary conditions for compressible flow problems.

Definition at line 1084 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetExpSize(), Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, m_gamma, m_pInf, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_traceNormals, m_uInf, m_vInf, m_wInf, npts, Vmath::Smul(), Vmath::Vabs(), Vmath::Vadd(), Vmath::Vdiv(), Vmath::Vmul(), Vmath::Vsqrt(), and Vmath::Vvtvp().

Referenced by SetCommonBC().

1088  {
1089  int i, j;
1090  int nTracePts = GetTraceTotPoints();
1091  int nVariables = physarray.num_elements();
1092  int nDimensions = m_spacedim;
1093 
1094  const Array<OneD, const int> &traceBndMap
1095  = m_fields[0]->GetTraceBndMap();
1096 
1097  NekDouble gamma = m_gamma;
1098  NekDouble gammaMinusOne = gamma - 1.0;
1099  NekDouble gammaMinusOneInv = 1.0 / gammaMinusOne;
1100 
1101  Array<OneD, NekDouble> tmp1 (nTracePts, 0.0);
1102  Array<OneD, NekDouble> tmp2 (nTracePts, 0.0);
1103  Array<OneD, NekDouble> VnInf(nTracePts, 0.0);
1104  Array<OneD, NekDouble> velInf(nDimensions, 0.0);
1105 
1106  // Computing the normal velocity for characteristics coming
1107  // from outside the computational domain
1108  velInf[0] = m_uInf;
1109  Vmath::Smul(nTracePts, m_uInf, m_traceNormals[0], 1, VnInf, 1);
1110  if (nDimensions == 2 || nDimensions == 3)
1111  {
1112  velInf[1] = m_vInf;
1113  Vmath::Smul(nTracePts, m_vInf, m_traceNormals[1], 1, tmp1, 1);
1114  Vmath::Vadd(nTracePts, VnInf, 1, tmp1, 1, VnInf, 1);
1115  }
1116  if (nDimensions == 3)
1117  {
1118  velInf[2] = m_wInf;
1119  Vmath::Smul(nTracePts, m_wInf, m_traceNormals[2], 1, tmp2, 1);
1120  Vmath::Vadd(nTracePts, VnInf, 1, tmp2, 1, VnInf, 1);
1121  }
1122 
1123  // Get physical values of the forward trace
1124  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
1125  for (i = 0; i < nVariables; ++i)
1126  {
1127  Fwd[i] = Array<OneD, NekDouble>(nTracePts);
1128  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
1129  }
1130 
1131  // Computing the normal velocity for characteristics coming
1132  // from inside the computational domain
1133  Array<OneD, NekDouble > Vn (nTracePts, 0.0);
1134  Array<OneD, NekDouble > Vel(nTracePts, 0.0);
1135  for (i = 0; i < nDimensions; ++i)
1136  {
1137  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, Vel, 1);
1138  Vmath::Vvtvp(nTracePts, m_traceNormals[i], 1, Vel, 1, Vn, 1, Vn, 1);
1139  }
1140 
1141  // Computing the absolute value of the velocity in order to compute the
1142  // Mach number to decide whether supersonic or subsonic
1143  Array<OneD, NekDouble > absVel(nTracePts, 0.0);
1144  for (i = 0; i < nDimensions; ++i)
1145  {
1146  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, tmp1, 1);
1147  Vmath::Vmul(nTracePts, tmp1, 1, tmp1, 1, tmp1, 1);
1148  Vmath::Vadd(nTracePts, tmp1, 1, absVel, 1, absVel, 1);
1149  }
1150  Vmath::Vsqrt(nTracePts, absVel, 1, absVel, 1);
1151 
1152  // Get speed of sound
1153  Array<OneD, NekDouble > soundSpeed(nTracePts);
1154  Array<OneD, NekDouble > pressure (nTracePts);
1155 
1156  for (i = 0; i < nTracePts; i++)
1157  {
1158  if (m_spacedim == 1)
1159  {
1160  pressure[i] = (gammaMinusOne) * (Fwd[2][i] -
1161  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i]));
1162  }
1163  else if (m_spacedim == 2)
1164  {
1165  pressure[i] = (gammaMinusOne) * (Fwd[3][i] -
1166  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1167  Fwd[2][i] * Fwd[2][i] / Fwd[0][i]));
1168  }
1169  else
1170  {
1171  pressure[i] = (gammaMinusOne) * (Fwd[4][i] -
1172  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1173  Fwd[2][i] * Fwd[2][i] / Fwd[0][i] +
1174  Fwd[3][i] * Fwd[3][i] / Fwd[0][i]));
1175  }
1176 
1177  soundSpeed[i] = sqrt(gamma * pressure[i] / Fwd[0][i]);
1178  }
1179 
1180  // Get Mach
1181  Array<OneD, NekDouble > Mach(nTracePts, 0.0);
1182  Vmath::Vdiv(nTracePts, Vn, 1, soundSpeed, 1, Mach, 1);
1183  Vmath::Vabs(nTracePts, Mach, 1, Mach, 1);
1184 
1185  // Auxiliary variables
1186  int e, id1, id2, npts, pnt;
1187  NekDouble rhoeb;
1188 
1189  // Loop on the bcRegions
1190  for (e = 0; e < m_fields[0]->GetBndCondExpansions()[bcRegion]->
1191  GetExpSize(); ++e)
1192  {
1193  npts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1194  GetExp(e)->GetTotPoints();
1195  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1196  GetPhys_Offset(e) ;
1197  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
1198 
1199  // Loop on points of bcRegion 'e'
1200  for (i = 0; i < npts; i++)
1201  {
1202  pnt = id2+i;
1203 
1204  // Subsonic flows
1205  if (Mach[pnt] < 0.99)
1206  {
1207  // Kinetic energy calculation
1208  NekDouble Ek = 0.0;
1209  for (j = 1; j < nVariables-1; ++j)
1210  {
1211  Ek += 0.5 * (Fwd[j][pnt] * Fwd[j][pnt]) / Fwd[0][pnt];
1212  }
1213 
1214  rhoeb = m_pInf * gammaMinusOneInv + Ek;
1215 
1216  // Partial extrapolation for subsonic cases
1217  for (j = 0; j < nVariables-1; ++j)
1218  {
1219  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1220  UpdatePhys())[id1+i] = Fwd[j][pnt];
1221  }
1222 
1223  (m_fields[nVariables-1]->GetBndCondExpansions()[bcRegion]->
1224  UpdatePhys())[id1+i] = rhoeb;
1225  }
1226  // Supersonic flows
1227  else
1228  {
1229  for (j = 0; j < nVariables; ++j)
1230  {
1231  // Extrapolation for supersonic cases
1232  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1233  UpdatePhys())[id1+i] = Fwd[j][pnt];
1234  }
1235  }
1236  }
1237  }
1238  }
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Vmath::Vabs
void Vabs(int n, const T *x, const int incx, T *y, const int incy)
vabs: y = |x|
Definition: Vmath.cpp:410
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
npts
static std::string npts
Definition: InputFld.cpp:43
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::GetExpSize
SOLVER_UTILS_EXPORT int GetExpSize()
Definition: EquationSystem.h:853
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::PressureOutflowFileBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Pressure outflow boundary conditions for compressible flow problems.

Definition at line 1245 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetExpSize(), Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, m_gamma, m_pressureStorage, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_traceNormals, m_uInf, m_vInf, m_wInf, npts, Vmath::Smul(), Vmath::Vabs(), Vmath::Vadd(), Vmath::Vdiv(), Vmath::Vmul(), Vmath::Vsqrt(), and Vmath::Vvtvp().

Referenced by SetCommonBC().

1249  {
1250  int i, j;
1251  int nTracePts = GetTraceTotPoints();
1252  int nVariables = physarray.num_elements();
1253  int nDimensions = m_spacedim;
1254 
1255  const Array<OneD, const int> &traceBndMap
1256  = m_fields[0]->GetTraceBndMap();
1257 
1258  NekDouble gamma = m_gamma;
1259  NekDouble gammaMinusOne = gamma - 1.0;
1260  NekDouble gammaMinusOneInv = 1.0 / gammaMinusOne;
1261 
1262  Array<OneD, NekDouble> tmp1 (nTracePts, 0.0);
1263  Array<OneD, NekDouble> tmp2 (nTracePts, 0.0);
1264  Array<OneD, NekDouble> VnInf(nTracePts, 0.0);
1265  Array<OneD, NekDouble> velInf(nDimensions, 0.0);
1266 
1267  // Computing the normal velocity for characteristics coming
1268  // from outside the computational domain
1269  velInf[0] = m_uInf;
1270  Vmath::Smul(nTracePts, m_uInf, m_traceNormals[0], 1, VnInf, 1);
1271  if (nDimensions == 2 || nDimensions == 3)
1272  {
1273  velInf[1] = m_vInf;
1274  Vmath::Smul(nTracePts, m_vInf, m_traceNormals[1], 1, tmp1, 1);
1275  Vmath::Vadd(nTracePts, VnInf, 1, tmp1, 1, VnInf, 1);
1276  }
1277  if (nDimensions == 3)
1278  {
1279  velInf[2] = m_wInf;
1280  Vmath::Smul(nTracePts, m_wInf, m_traceNormals[2], 1, tmp2, 1);
1281  Vmath::Vadd(nTracePts, VnInf, 1, tmp2, 1, VnInf, 1);
1282  }
1283 
1284  // Get physical values of the forward trace
1285  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
1286 
1287  for (i = 0; i < nVariables; ++i)
1288  {
1289  Fwd[i] = Array<OneD, NekDouble>(nTracePts, 0.0);
1290  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
1291  }
1292 
1293  // Computing the normal velocity for characteristics coming
1294  // from inside the computational domain
1295  Array<OneD, NekDouble > Vn (nTracePts, 0.0);
1296  Array<OneD, NekDouble > Vel(nTracePts, 0.0);
1297  for (i = 0; i < nDimensions; ++i)
1298  {
1299  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, Vel, 1);
1300  Vmath::Vvtvp(nTracePts, m_traceNormals[i], 1, Vel, 1, Vn, 1, Vn, 1);
1301  }
1302 
1303  // Computing the absolute value of the velocity in order to compute the
1304  // Mach number to decide whether supersonic or subsonic
1305  Array<OneD, NekDouble > absVel(nTracePts, 0.0);
1306  for (i = 0; i < nDimensions; ++i)
1307  {
1308  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, tmp1, 1);
1309  Vmath::Vmul(nTracePts, tmp1, 1, tmp1, 1, tmp1, 1);
1310  Vmath::Vadd(nTracePts, tmp1, 1, absVel, 1, absVel, 1);
1311  }
1312  Vmath::Vsqrt(nTracePts, absVel, 1, absVel, 1);
1313 
1314  // Get speed of sound
1315  Array<OneD, NekDouble > soundSpeed (nTracePts, 0.0);
1316  Array<OneD, NekDouble > pressure (nTracePts, 0.0);
1317 
1318  for (i = 0; i < nTracePts; i++)
1319  {
1320  if (m_spacedim == 1)
1321  {
1322  pressure[i] = (gammaMinusOne) * (Fwd[2][i] -
1323  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i]));
1324  }
1325  else if (m_spacedim == 2)
1326  {
1327  pressure[i] = (gammaMinusOne) * (Fwd[3][i] -
1328  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1329  Fwd[2][i] * Fwd[2][i] / Fwd[0][i]));
1330  }
1331  else
1332  {
1333  pressure[i] = (gammaMinusOne) * (Fwd[4][i] -
1334  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1335  Fwd[2][i] * Fwd[2][i] / Fwd[0][i] +
1336  Fwd[3][i] * Fwd[3][i] / Fwd[0][i]));
1337  }
1338 
1339  soundSpeed[i] = sqrt(gamma * pressure[i] / Fwd[0][i]);
1340  }
1341 
1342  // Get Mach
1343  Array<OneD, NekDouble > Mach(nTracePts, 0.0);
1344  Vmath::Vdiv(nTracePts, Vn, 1, soundSpeed, 1, Mach, 1);
1345  Vmath::Vabs(nTracePts, Mach, 1, Mach, 1);
1346 
1347  // Auxiliary variables
1348  int e, id1, id2, npts, pnt;
1349  NekDouble rhoeb;
1350 
1351  // Loop on the bcRegions
1352  for (e = 0; e < m_fields[0]->GetBndCondExpansions()[bcRegion]->
1353  GetExpSize(); ++e)
1354  {
1355  npts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1356  GetExp(e)->GetTotPoints();
1357  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1358  GetPhys_Offset(e);
1359  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
1360 
1361  // Loop on points of bcRegion 'e'
1362  for (i = 0; i < npts; i++)
1363  {
1364  pnt = id2+i;
1365 
1366  // Subsonic flows
1367  if (Mach[pnt] < 0.99)
1368  {
1369  // Kinetic energy calculation
1370  NekDouble Ek = 0.0;
1371  for (j = 1; j < nVariables-1; ++j)
1372  {
1373  Ek += 0.5 * (Fwd[j][pnt] * Fwd[j][pnt]) / Fwd[0][pnt];
1374  }
1375 
1376  rhoeb = m_pressureStorage[id1+i] * gammaMinusOneInv + Ek;
1377 
1378  // Partial extrapolation for subsonic cases
1379  for (j = 0; j < nVariables-1; ++j)
1380  {
1381  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1382  UpdatePhys())[id1+i] = Fwd[j][pnt];
1383  }
1384 
1385  (m_fields[nVariables-1]->GetBndCondExpansions()[bcRegion]->
1386  UpdatePhys())[id1+i] = rhoeb;
1387  }
1388  // Supersonic flows
1389  else
1390  {
1391  for (j = 0; j < nVariables; ++j)
1392  {
1393  // Extrapolation for supersonic cases
1394  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1395  UpdatePhys())[id1+i] = Fwd[j][pnt];
1396  }
1397  }
1398  }
1399  }
1400  }
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Vmath::Vabs
void Vabs(int n, const T *x, const int incx, T *y, const int incy)
vabs: y = |x|
Definition: Vmath.cpp:410
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
npts
static std::string npts
Definition: InputFld.cpp:43
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::CompressibleFlowSystem::m_pressureStorage
Array< OneD, NekDouble > m_pressureStorage
Definition: CompressibleFlowSystem.h:129
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::GetExpSize
SOLVER_UTILS_EXPORT int GetExpSize()
Definition: EquationSystem.h:853
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::PressureOutflowNonReflectiveBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Pressure outflow non-reflective boundary conditions for compressible flow problems.

Definition at line 924 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetExpSize(), Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, m_gamma, m_pInf, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_traceNormals, m_uInf, m_vInf, m_wInf, npts, Vmath::Smul(), Vmath::Vabs(), Vmath::Vadd(), Vmath::Vdiv(), Vmath::Vmul(), Vmath::Vsqrt(), and Vmath::Vvtvp().

Referenced by SetCommonBC().

928  {
929  int i, j;
930  int nTracePts = GetTraceTotPoints();
931  int nVariables = physarray.num_elements();
932  int nDimensions = m_spacedim;
933 
934  const Array<OneD, const int> &traceBndMap
935  = m_fields[0]->GetTraceBndMap();
936 
937  NekDouble gamma = m_gamma;
938  NekDouble gammaMinusOne = gamma - 1.0;
939  NekDouble gammaMinusOneInv = 1.0 / gammaMinusOne;
940 
941  Array<OneD, NekDouble> tmp1 (nTracePts, 0.0);
942  Array<OneD, NekDouble> tmp2 (nTracePts, 0.0);
943  Array<OneD, NekDouble> VnInf(nTracePts, 0.0);
944  Array<OneD, NekDouble> velInf(nDimensions, 0.0);
945 
946  // Computing the normal velocity for characteristics coming
947  // from outside the computational domain
948  velInf[0] = m_uInf;
949  Vmath::Smul(nTracePts, m_uInf, m_traceNormals[0], 1, VnInf, 1);
950  if (nDimensions == 2 || nDimensions == 3)
951  {
952  velInf[1] = m_vInf;
953  Vmath::Smul(nTracePts, m_vInf, m_traceNormals[1], 1, tmp1, 1);
954  Vmath::Vadd(nTracePts, VnInf, 1, tmp1, 1, VnInf, 1);
955  }
956  if (nDimensions == 3)
957  {
958  velInf[2] = m_wInf;
959  Vmath::Smul(nTracePts, m_wInf, m_traceNormals[2], 1, tmp2, 1);
960  Vmath::Vadd(nTracePts, VnInf, 1, tmp2, 1, VnInf, 1);
961  }
962 
963  // Get physical values of the forward trace
964  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
965  for (i = 0; i < nVariables; ++i)
966  {
967  Fwd[i] = Array<OneD, NekDouble>(nTracePts);
968  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
969  }
970 
971  // Computing the normal velocity for characteristics coming
972  // from inside the computational domain
973  Array<OneD, NekDouble > Vn (nTracePts, 0.0);
974  Array<OneD, NekDouble > Vel(nTracePts, 0.0);
975  for (i = 0; i < nDimensions; ++i)
976  {
977  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, Vel, 1);
978  Vmath::Vvtvp(nTracePts, m_traceNormals[i], 1, Vel, 1, Vn, 1, Vn, 1);
979  }
980 
981  // Computing the absolute value of the velocity in order to compute the
982  // Mach number to decide whether supersonic or subsonic
983  Array<OneD, NekDouble > absVel(nTracePts, 0.0);
984  for (i = 0; i < nDimensions; ++i)
985  {
986  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, tmp1, 1);
987  Vmath::Vmul(nTracePts, tmp1, 1, tmp1, 1, tmp1, 1);
988  Vmath::Vadd(nTracePts, tmp1, 1, absVel, 1, absVel, 1);
989  }
990  Vmath::Vsqrt(nTracePts, absVel, 1, absVel, 1);
991 
992  // Get speed of sound
993  Array<OneD, NekDouble > soundSpeed(nTracePts);
994  Array<OneD, NekDouble > pressure (nTracePts);
995 
996  for (i = 0; i < nTracePts; i++)
997  {
998  if (m_spacedim == 1)
999  {
1000  pressure[i] = (gammaMinusOne) * (Fwd[2][i] -
1001  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i]));
1002  }
1003  else if (m_spacedim == 2)
1004  {
1005  pressure[i] = (gammaMinusOne) * (Fwd[3][i] -
1006  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1007  Fwd[2][i] * Fwd[2][i] / Fwd[0][i]));
1008  }
1009  else
1010  {
1011  pressure[i] = (gammaMinusOne) * (Fwd[4][i] -
1012  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
1013  Fwd[2][i] * Fwd[2][i] / Fwd[0][i] +
1014  Fwd[3][i] * Fwd[3][i] / Fwd[0][i]));
1015  }
1016 
1017  soundSpeed[i] = sqrt(gamma * pressure[i] / Fwd[0][i]);
1018  }
1019 
1020  // Get Mach
1021  Array<OneD, NekDouble > Mach(nTracePts, 0.0);
1022  Vmath::Vdiv(nTracePts, Vn, 1, soundSpeed, 1, Mach, 1);
1023  Vmath::Vabs(nTracePts, Mach, 1, Mach, 1);
1024 
1025  // Auxiliary variables
1026  int e, id1, id2, npts, pnt;
1027  NekDouble rhoeb;
1028 
1029  // Loop on the bcRegions
1030  for (e = 0; e < m_fields[0]->GetBndCondExpansions()[bcRegion]->
1031  GetExpSize(); ++e)
1032  {
1033  npts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1034  GetExp(e)->GetTotPoints();
1035  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
1036  GetPhys_Offset(e) ;
1037  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
1038 
1039  // Loop on points of bcRegion 'e'
1040  for (i = 0; i < npts; i++)
1041  {
1042  pnt = id2+i;
1043 
1044  // Subsonic flows
1045  if (Mach[pnt] < 0.99)
1046  {
1047  // Kinetic energy calculation
1048  NekDouble Ek = 0.0;
1049  for (j = 1; j < nVariables-1; ++j)
1050  {
1051  Ek += 0.5 * (Fwd[j][pnt] * Fwd[j][pnt]) / Fwd[0][pnt];
1052  }
1053 
1054  rhoeb = m_pInf * gammaMinusOneInv + Ek;
1055 
1056  // Partial extrapolation for subsonic cases
1057  for (j = 0; j < nVariables-1; ++j)
1058  {
1059  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1060  UpdatePhys())[id1+i] = Fwd[j][pnt];
1061  }
1062 
1063  (m_fields[nVariables-1]->GetBndCondExpansions()[bcRegion]->
1064  UpdatePhys())[id1+i] = 2.0 * rhoeb - Fwd[nVariables-1][pnt];
1065  }
1066  // Supersonic flows
1067  else
1068  {
1069  for (j = 0; j < nVariables; ++j)
1070  {
1071  // Extrapolation for supersonic cases
1072  (m_fields[j]->GetBndCondExpansions()[bcRegion]->
1073  UpdatePhys())[id1+i] = Fwd[j][pnt];
1074  }
1075  }
1076  }
1077  }
1078  }
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Vmath::Vabs
void Vabs(int n, const T *x, const int incx, T *y, const int incy)
vabs: y = |x|
Definition: Vmath.cpp:410
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
npts
static std::string npts
Definition: InputFld.cpp:43
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::GetExpSize
SOLVER_UTILS_EXPORT int GetExpSize()
Definition: EquationSystem.h:853
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::RiemannInvariantBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Outflow characteristic boundary conditions for compressible flow problems.

Definition at line 667 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, m_gamma, m_pInf, m_rhoInf, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_traceNormals, m_uInf, m_vInf, m_wInf, Vmath::Smul(), Vmath::Vabs(), Vmath::Vadd(), Vmath::Vdiv(), Vmath::Vmul(), Vmath::Vsqrt(), and Vmath::Vvtvp().

Referenced by SetCommonBC().

671  {
672  int i, j;
673  int nTracePts = GetTraceTotPoints();
674  int nVariables = physarray.num_elements();
675  int nDimensions = m_spacedim;
676 
677  const Array<OneD, const int> &traceBndMap
678  = m_fields[0]->GetTraceBndMap();
679 
680  NekDouble gamma = m_gamma;
681  NekDouble gammaInv = 1.0 / gamma;
682  NekDouble gammaMinusOne = gamma - 1.0;
683  NekDouble gammaMinusOneInv = 1.0 / gammaMinusOne;
684 
685  Array<OneD, NekDouble> tmp1 (nTracePts, 0.0);
686  Array<OneD, NekDouble> tmp2 (nTracePts, 0.0);
687  Array<OneD, NekDouble> VnInf(nTracePts, 0.0);
688  Array<OneD, NekDouble> velInf(nDimensions, 0.0);
689 
690  // Computing the normal velocity for characteristics coming
691  // from outside the computational domain
692  velInf[0] = m_uInf;
693  Vmath::Smul(nTracePts, m_uInf, m_traceNormals[0], 1, VnInf, 1);
694  if (nDimensions == 2 || nDimensions == 3)
695  {
696  velInf[1] = m_vInf;
697  Vmath::Smul(nTracePts, m_vInf, m_traceNormals[1], 1, tmp1, 1);
698  Vmath::Vadd(nTracePts, VnInf, 1, tmp1, 1, VnInf, 1);
699  }
700  if (nDimensions == 3)
701  {
702  velInf[2] = m_wInf;
703  Vmath::Smul(nTracePts, m_wInf, m_traceNormals[2], 1, tmp2, 1);
704  Vmath::Vadd(nTracePts, VnInf, 1, tmp2, 1, VnInf, 1);
705  }
706 
707  // Get physical values of the forward trace
708  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
709  for (i = 0; i < nVariables; ++i)
710  {
711  Fwd[i] = Array<OneD, NekDouble>(nTracePts);
712  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
713  }
714 
715  // Computing the normal velocity for characteristics coming
716  // from inside the computational domain
717  Array<OneD, NekDouble > Vn (nTracePts, 0.0);
718  Array<OneD, NekDouble > Vel(nTracePts, 0.0);
719  for (i = 0; i < nDimensions; ++i)
720  {
721  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, Vel, 1);
722  Vmath::Vvtvp(nTracePts, m_traceNormals[i], 1, Vel, 1, Vn, 1, Vn, 1);
723  }
724 
725  // Computing the absolute value of the velocity in order to compute the
726  // Mach number to decide whether supersonic or subsonic
727  Array<OneD, NekDouble > absVel(nTracePts, 0.0);
728  for (i = 0; i < nDimensions; ++i)
729  {
730  Vmath::Vdiv(nTracePts, Fwd[i+1], 1, Fwd[0], 1, tmp1, 1);
731  Vmath::Vmul(nTracePts, tmp1, 1, tmp1, 1, tmp1, 1);
732  Vmath::Vadd(nTracePts, tmp1, 1, absVel, 1, absVel, 1);
733  }
734  Vmath::Vsqrt(nTracePts, absVel, 1, absVel, 1);
735 
736  // Get speed of sound
737  Array<OneD, NekDouble > soundSpeed(nTracePts);
738  Array<OneD, NekDouble > pressure (nTracePts);
739 
740  for (i = 0; i < nTracePts; i++)
741  {
742  if (m_spacedim == 1)
743  {
744  pressure[i] = (gammaMinusOne) * (Fwd[2][i] -
745  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i]));
746  }
747  else if (m_spacedim == 2)
748  {
749  pressure[i] = (gammaMinusOne) * (Fwd[3][i] -
750  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
751  Fwd[2][i] * Fwd[2][i] / Fwd[0][i]));
752  }
753  else
754  {
755  pressure[i] = (gammaMinusOne) * (Fwd[4][i] -
756  0.5 * (Fwd[1][i] * Fwd[1][i] / Fwd[0][i] +
757  Fwd[2][i] * Fwd[2][i] / Fwd[0][i] +
758  Fwd[3][i] * Fwd[3][i] / Fwd[0][i]));
759  }
760 
761  soundSpeed[i] = sqrt(gamma * pressure[i] / Fwd[0][i]);
762  }
763 
764  // Get Mach
765  Array<OneD, NekDouble > Mach(nTracePts, 0.0);
766  Vmath::Vdiv(nTracePts, Vn, 1, soundSpeed, 1, Mach, 1);
767  Vmath::Vabs(nTracePts, Mach, 1, Mach, 1);
768 
769  // Auxiliary variables
770  int eMax;
771  int e, id1, id2, nBCEdgePts, pnt;
772  NekDouble cPlus, rPlus, cMinus, rMinus, VDBC, VNBC;
773  Array<OneD, NekDouble> velBC(nDimensions, 0.0);
774  Array<OneD, NekDouble> rhoVelBC(nDimensions, 0.0);
775  NekDouble rhoBC, EBC, cBC, sBC, pBC;
776 
777  eMax = m_fields[0]->GetBndCondExpansions()[bcRegion]->GetExpSize();
778 
779  // Loop on bcRegions
780  for (e = 0; e < eMax; ++e)
781  {
782  nBCEdgePts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
783  GetExp(e)->GetTotPoints();
784 
785  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
786  GetPhys_Offset(e);
787  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
788 
789  // Loop on the points of the bcRegion
790  for (i = 0; i < nBCEdgePts; i++)
791  {
792  pnt = id2+i;
793 
794  // Impose inflow Riemann invariant
795  if (Vn[pnt] <= 0.0)
796  {
797  // Subsonic flows
798  if (Mach[pnt] < 1.00)
799  {
800  // + Characteristic from inside
801  cPlus = sqrt(gamma * pressure[pnt] / Fwd[0][pnt]);
802  rPlus = Vn[pnt] + 2.0 * cPlus * gammaMinusOneInv;
803 
804  // - Characteristic from boundary
805  cMinus = sqrt(gamma * m_pInf / m_rhoInf);
806  rMinus = VnInf[pnt] - 2.0 * cMinus * gammaMinusOneInv;
807  }
808  else
809  {
810  // + Characteristic from inside
811  cPlus = sqrt(gamma * m_pInf / m_rhoInf);
812  rPlus = VnInf[pnt] + 2.0 * cPlus * gammaMinusOneInv;
813 
814  // + Characteristic from inside
815  cMinus = sqrt(gamma * m_pInf / m_rhoInf);
816  rMinus = VnInf[pnt] - 2.0 * cPlus * gammaMinusOneInv;
817  }
818 
819  // Riemann boundary variables
820  VNBC = 0.5 * (rPlus + rMinus);
821  cBC = 0.25 * gammaMinusOne * (rPlus - rMinus);
822  VDBC = VNBC - VnInf[pnt];
823 
824  // Thermodynamic boundary variables
825  sBC = m_pInf / (pow(m_rhoInf, gamma));
826  rhoBC = pow((cBC * cBC) / (gamma * sBC), gammaMinusOneInv);
827  pBC = rhoBC * cBC * cBC * gammaInv;
828 
829  // Kinetic energy initialiasation
830  NekDouble EkBC = 0.0;
831 
832  // Boundary velocities
833  for ( j = 0; j < nDimensions; ++j)
834  {
835  velBC[j] = velInf[j] + VDBC * m_traceNormals[j][pnt];
836  rhoVelBC[j] = rhoBC * velBC[j];
837  EkBC += 0.5 * rhoBC * velBC[j]*velBC[j];
838  }
839 
840  // Boundary energy
841  EBC = pBC * gammaMinusOneInv + EkBC;
842 
843  // Imposing Riemann Invariant boundary conditions
844  (m_fields[0]->GetBndCondExpansions()[bcRegion]->
845  UpdatePhys())[id1+i] = rhoBC;
846  for (j = 0; j < nDimensions; ++j)
847  {
848  (m_fields[j+1]->GetBndCondExpansions()[bcRegion]->
849  UpdatePhys())[id1+i] = rhoVelBC[j];
850  }
851  (m_fields[nDimensions+1]->GetBndCondExpansions()[bcRegion]->
852  UpdatePhys())[id1+i] = EBC;
853 
854  }
855  else // Impose outflow Riemann invariant
856  {
857  // Subsonic flows
858  if (Mach[pnt] < 1.00)
859  {
860  // + Characteristic from inside
861  cPlus = sqrt(gamma * pressure[pnt] / Fwd[0][pnt]);
862  rPlus = Vn[pnt] + 2.0 * cPlus * gammaMinusOneInv;
863 
864  // - Characteristic from boundary
865  cMinus = sqrt(gamma * m_pInf / m_rhoInf);
866  rMinus = VnInf[pnt] - 2.0 * cMinus * gammaMinusOneInv;
867  }
868  else
869  {
870  // + Characteristic from inside
871  cPlus = sqrt(gamma * pressure[pnt] / Fwd[0][pnt]);
872  rPlus = Vn[pnt] + 2.0 * cPlus * gammaMinusOneInv;
873 
874  // + Characteristic from inside
875  cMinus = sqrt(gamma * pressure[pnt] / Fwd[0][pnt]);
876  rMinus = Vn[pnt] - 2.0 * cPlus * gammaMinusOneInv;
877  }
878 
879  // Riemann boundary variables
880  VNBC = 0.5 * (rPlus + rMinus);
881  cBC = 0.25 * gammaMinusOne * (rPlus - rMinus);
882  VDBC = VNBC - Vn[pnt];
883 
884  // Thermodynamic boundary variables
885  sBC = pressure[pnt] / (pow(Fwd[0][pnt], gamma));
886  rhoBC = pow((cBC * cBC) / (gamma * sBC), gammaMinusOneInv);
887  pBC = rhoBC * cBC * cBC * gammaInv;
888 
889  // Kinetic energy initialiasation
890  NekDouble EkBC = 0.0;
891 
892  // Boundary velocities
893  for ( j = 0; j < nDimensions; ++j)
894  {
895  velBC[j] = Fwd[j+1][pnt] / Fwd[0][pnt] +
896  VDBC * m_traceNormals[j][pnt];
897  rhoVelBC[j] = rhoBC * velBC[j];
898  EkBC += 0.5 * rhoBC * velBC[j]*velBC[j];
899  }
900 
901  // Boundary energy
902  EBC = pBC * gammaMinusOneInv + EkBC;
903 
904  // Imposing Riemann Invariant boundary conditions
905  (m_fields[0]->GetBndCondExpansions()[bcRegion]->
906  UpdatePhys())[id1+i] = rhoBC;
907  for (j = 0; j < nDimensions; ++j)
908  {
909  (m_fields[j+1]->GetBndCondExpansions()[bcRegion]->
910  UpdatePhys())[id1+i] = rhoVelBC[j];
911  }
912  (m_fields[nDimensions+1]->GetBndCondExpansions()[bcRegion]->
913  UpdatePhys())[id1+i] = EBC;
914  }
915  }
916  }
917  }
Vmath::Vsqrt
void Vsqrt(int n, const T *x, const int incx, T *y, const int incy)
sqrt y = sqrt(x)
Definition: Vmath.cpp:394
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Vmath::Vdiv
void Vdiv(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x/y.
Definition: Vmath.cpp:227
Vmath::Vabs
void Vabs(int n, const T *x, const int incx, T *y, const int incy)
vabs: y = |x|
Definition: Vmath.cpp:410
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Vmath::Vadd
void Vadd(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Add vector z = x+y.
Definition: Vmath.cpp:285
Vmath::Vmul
void Vmul(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Multiply vector z = x*y.
Definition: Vmath.cpp:169
void Nektar::CompressibleFlowSystem::SetCommonBC ( const std::string &  userDefStr,
const int  n,
const NekDouble  time,
int &  cnt,
Array< OneD, Array< OneD, NekDouble > > &  inarray 
)
protected

Set boundary conditions which can be: a) Wall and Symmerty BCs implemented at CompressibleFlowSystem level since they are compressible solver specific; b) Time dependent BCs.

Parameters
inarrayfields array.
timetime.

Definition at line 322 of file CompressibleFlowSystem.cpp.

References ASSERTL0, ExtrapOrder0BC(), Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_session, PressureInflowFileBC(), PressureOutflowBC(), PressureOutflowFileBC(), PressureOutflowNonReflectiveBC(), RiemannInvariantBC(), SymmetryBC(), WallBC(), and WallViscousBC().

Referenced by Nektar::NavierStokesCFE::SetBoundaryConditions(), Nektar::EulerADCFE::SetBoundaryConditions(), and Nektar::EulerCFE::SetBoundaryConditions().

328  {
329  std::string varName;
330  int nvariables = m_fields.num_elements();
331 
332  if(!userDefStr.empty())
333  {
334  if(boost::iequals(userDefStr,"Wall"))
335  {
336  WallBC(n, cnt, inarray);
337  }
338  else if(boost::iequals(userDefStr,"WallViscous") ||
339  boost::iequals(userDefStr,"WallAdiabatic"))
340  {
341  // Wall Boundary Condition
342  WallViscousBC(n, cnt, inarray);
343  }
344  else if(boost::iequals(userDefStr,"Symmetry"))
345  {
346  // Symmetric Boundary Condition
347  SymmetryBC(n, cnt, inarray);
348  }
349  else if(boost::iequals(userDefStr,"RiemannInvariant"))
350  {
351  // Riemann invariant characteristic Boundary Condition
352  RiemannInvariantBC(n, cnt, inarray);
353  }
354  else if(boost::iequals(userDefStr,"PressureOutflowNonReflective"))
355  {
356  // Pressure outflow non-reflective Boundary Condition
357  PressureOutflowNonReflectiveBC(n, cnt, inarray);
358  }
359  else if(boost::iequals(userDefStr,"PressureOutflow"))
360  {
361  // Pressure outflow Boundary Condition
362  PressureOutflowBC(n, cnt, inarray);
363  }
364  else if(boost::iequals(userDefStr,"PressureOutflowFile"))
365  {
366  // Pressure outflow Boundary Condition from file
367  PressureOutflowFileBC(n, cnt, inarray);
368  }
369  else if(boost::iequals(userDefStr,"PressureInflowFile"))
370  {
371  // Pressure inflow Boundary Condition from file
372  PressureInflowFileBC(n, cnt, inarray);
373  }
374  else if(boost::iequals(userDefStr,"ExtrapOrder0"))
375  {
376  // Extrapolation of the data at the boundaries
377  ExtrapOrder0BC(n, cnt, inarray);
378  }
379  else if(boost::iequals(userDefStr,"TimeDependent"))
380  {
381  for (int i = 0; i < nvariables; ++i)
382  {
383  varName = m_session->GetVariable(i);
384  m_fields[i]->EvaluateBoundaryConditions(time, varName);
385  }
386  }
387  else
388  {
389  string errmsg = "Unrecognised boundary condition: ";
390  errmsg += userDefStr;
391  ASSERTL0(false,errmsg.c_str());
392  }
393  }
394  }
Nektar::CompressibleFlowSystem::ExtrapOrder0BC
void ExtrapOrder0BC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Extrapolation of order 0 for all the variables such that, at the boundaries, a trivial Riemann proble...
Definition: CompressibleFlowSystem.cpp:1572
Nektar::CompressibleFlowSystem::RiemannInvariantBC
void RiemannInvariantBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Outflow characteristic boundary conditions for compressible flow problems.
Definition: CompressibleFlowSystem.cpp:667
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::CompressibleFlowSystem::SymmetryBC
void SymmetryBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Symmetry boundary conditions for compressible flow problems.
Definition: CompressibleFlowSystem.cpp:571
Nektar::CompressibleFlowSystem::PressureOutflowNonReflectiveBC
void PressureOutflowNonReflectiveBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Pressure outflow non-reflective boundary conditions for compressible flow problems.
Definition: CompressibleFlowSystem.cpp:924
Nektar::CompressibleFlowSystem::PressureOutflowFileBC
void PressureOutflowFileBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Pressure outflow boundary conditions for compressible flow problems.
Definition: CompressibleFlowSystem.cpp:1245
Nektar::CompressibleFlowSystem::PressureOutflowBC
void PressureOutflowBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Pressure outflow boundary conditions for compressible flow problems.
Definition: CompressibleFlowSystem.cpp:1084
Nektar::CompressibleFlowSystem::WallViscousBC
void WallViscousBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Wall boundary conditions for viscous compressible flow problems.
Definition: CompressibleFlowSystem.cpp:496
Nektar::CompressibleFlowSystem::WallBC
void WallBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Wall boundary conditions for compressible flow problems.
Definition: CompressibleFlowSystem.cpp:399
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::m_session
LibUtilities::SessionReaderSharedPtr m_session
The session reader.
Definition: EquationSystem.h:452
Nektar::CompressibleFlowSystem::PressureInflowFileBC
void PressureInflowFileBC(int bcRegion, int cnt, Array< OneD, Array< OneD, NekDouble > > &physarray)
Pressure inflow boundary conditions for compressible flow problems where either the density and the v...
Definition: CompressibleFlowSystem.cpp:1409
void Nektar::CompressibleFlowSystem::SetVarPOrderElmt ( const Array< OneD, const Array< OneD, NekDouble > > &  physfield,
Array< OneD, NekDouble > &  PolyOrder 
)
protected
void Nektar::CompressibleFlowSystem::SymmetryBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Symmetry boundary conditions for compressible flow problems.

Definition at line 571 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_traceNormals, Vmath::Smul(), Vmath::Vcopy(), Vmath::Vsub(), and Vmath::Vvtvp().

Referenced by SetCommonBC().

575  {
576  int i;
577  int nTracePts = GetTraceTotPoints();
578  int nVariables = physarray.num_elements();
579 
580  const Array<OneD, const int> &traceBndMap
581  = m_fields[0]->GetTraceBndMap();
582 
583  // Get physical values of the forward trace (from exp to phys)
584  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
585  for (i = 0; i < nVariables; ++i)
586  {
587  Fwd[i] = Array<OneD, NekDouble>(nTracePts);
588  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
589  }
590 
591  // Take into account that for PDE based shock capturing, eps = 0 at the
592  // wall.
593  int e, id1, id2, nBCEdgePts, eMax;
594 
595  eMax = m_fields[0]->GetBndCondExpansions()[bcRegion]->GetExpSize();
596 
597  for (e = 0; e < eMax; ++e)
598  {
599  nBCEdgePts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
600  GetExp(e)->GetTotPoints();
601  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
602  GetPhys_Offset(e);
603  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
604 
605  if (nVariables == m_spacedim+3)
606  {
607  NekDouble factor = 0.0;
608  NekDouble factor2 = 1.0;
609 
610  Array<OneD, NekDouble > tmp2(nBCEdgePts, 0.0);
611  Vmath::Smul(nBCEdgePts,
612  factor,
613  &Fwd[nVariables-1][id2], 1,
614  &tmp2[0], 1);
615 
616  Vmath::Vsub(nBCEdgePts,
617  &Fwd[nVariables-1][id2], 1,
618  &tmp2[0], 1,
619  &Fwd[nVariables-1][id2], 1);
620 
621  Vmath::Smul(nBCEdgePts,
622  factor2,
623  &Fwd[nVariables-1][id2], 1,
624  &Fwd[nVariables-1][id2], 1);
625  }
626 
627  // For 2D/3D, define: v* = v - 2(v.n)n
628  Array<OneD, NekDouble> tmp(nBCEdgePts, 0.0);
629 
630  // Calculate (v.n)
631  for (i = 0; i < m_spacedim; ++i)
632  {
633  Vmath::Vvtvp(nBCEdgePts,
634  &Fwd[1+i][id2], 1,
635  &m_traceNormals[i][id2], 1,
636  &tmp[0], 1,
637  &tmp[0], 1);
638  }
639 
640  // Calculate 2.0(v.n)
641  Vmath::Smul(nBCEdgePts, -2.0, &tmp[0], 1, &tmp[0], 1);
642 
643  // Calculate v* = v - 2.0(v.n)n
644  for (i = 0; i < m_spacedim; ++i)
645  {
646  Vmath::Vvtvp(nBCEdgePts,
647  &tmp[0], 1,
648  &m_traceNormals[i][id2], 1,
649  &Fwd[1+i][id2], 1,
650  &Fwd[1+i][id2], 1);
651  }
652 
653  // Copy boundary adjusted values into the boundary expansion
654  for (i = 0; i < nVariables; ++i)
655  {
656  Vmath::Vcopy(nBCEdgePts, &Fwd[i][id2], 1,
657  &(m_fields[i]->GetBndCondExpansions()[bcRegion]->
658  UpdatePhys())[id1], 1);
659  }
660  }
661  }
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Vmath::Vsub
void Vsub(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Subtract vector z = x-y.
Definition: Vmath.cpp:329
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
virtual void Nektar::CompressibleFlowSystem::v_ExtraFldOutput ( std::vector< Array< OneD, NekDouble > > &  fieldcoeffs,
std::vector< std::string > &  variables 
)
protectedvirtual

Reimplemented from Nektar::SolverUtils::EquationSystem.

void Nektar::CompressibleFlowSystem::v_GenerateSummary ( SolverUtils::SummaryList &  s)
protectedvirtual

Print a summary of time stepping parameters.

Print out a summary with some relevant information.

Reimplemented from Nektar::SolverUtils::UnsteadySystem.

Reimplemented in Nektar::EulerADCFE, Nektar::EulerCFE, and Nektar::NavierStokesCFE.

Definition at line 308 of file CompressibleFlowSystem.cpp.

Referenced by Nektar::NavierStokesCFE::v_GenerateSummary(), Nektar::EulerCFE::v_GenerateSummary(), and Nektar::EulerADCFE::v_GenerateSummary().

309  {
310  UnsteadySystem::v_GenerateSummary(s);
311  }
virtual NekDouble Nektar::CompressibleFlowSystem::v_GetTimeStep ( const Array< OneD, const Array< OneD, NekDouble > > &  inarray)
protectedvirtual

Return the timestep to be used for the next step in the time-marching loop.

See also
UnsteadySystem::GetTimeStep

Reimplemented from Nektar::SolverUtils::UnsteadySystem.

void Nektar::CompressibleFlowSystem::v_InitObject ( )
protectedvirtual

Initialization object for CompressibleFlowSystem class.

Reimplemented from Nektar::SolverUtils::UnsteadySystem.

Reimplemented in Nektar::EulerADCFE, Nektar::NavierStokesCFE, and Nektar::EulerCFE.

Definition at line 63 of file CompressibleFlowSystem.cpp.

References ASSERTL0, Nektar::LibUtilities::NekFactory< tKey, tBase, >::CreateInstance(), Nektar::MultiRegions::eDiscontinuous, Nektar::MultiRegions::eGalerkin, Nektar::SolverUtils::GetAdvectionFactory(), GetArtificialDynamicViscosity(), Nektar::SolverUtils::GetDiffusionFactory(), GetFluxVector(), GetFluxVectorDeAlias(), GetGamma(), GetNormals(), Nektar::SolverUtils::EquationSystem::GetPressure(), Nektar::SolverUtils::GetRiemannSolverFactory(), GetSmoothArtificialViscosity(), GetVecLocs(), GetViscousFluxVector(), GetViscousFluxVectorDeAlias(), Nektar::SolverUtils::Forcing::Load(), m_advection, m_amplitude, m_C1, m_C2, m_Cp, m_diffusion, m_eps_max, m_EqTypeStr, m_FacH, m_FacL, Nektar::SolverUtils::EquationSystem::m_fields, m_fieldStorage, m_forcing, m_gamma, m_gasConstant, m_hFactor, Nektar::SolverUtils::UnsteadySystem::m_homoInitialFwd, m_Kappa, m_mu, m_mu0, m_omega, m_pInf, m_Prandtl, m_pressureStorage, Nektar::SolverUtils::EquationSystem::m_projectionType, m_rhoInf, m_riemannSolver, m_riemannSolverLDG, Nektar::SolverUtils::EquationSystem::m_session, m_shockCaptureType, m_Skappa, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_specHP_dealiasing, m_steadyStateTol, m_thermalConductivity, m_Twall, m_uInf, m_UInf, m_vecLocs, m_vInf, m_ViscosityType, m_wInf, and Vmath::Vcopy().

Referenced by Nektar::EulerCFE::v_InitObject(), Nektar::NavierStokesCFE::v_InitObject(), and Nektar::EulerADCFE::v_InitObject().

64  {
65  UnsteadySystem::v_InitObject();
66 
67  ASSERTL0(m_session->DefinesSolverInfo("UPWINDTYPE"),
68  "No UPWINDTYPE defined in session.");
69 
70  // Do not forwards transform initial condition
71  m_homoInitialFwd = false;
72 
73  // Set up locations of velocity vector.
74  m_vecLocs = Array<OneD, Array<OneD, NekDouble> >(1);
75  m_vecLocs[0] = Array<OneD, NekDouble>(m_spacedim);
76  for (int i = 0; i < m_spacedim; ++i)
77  {
78  m_vecLocs[0][i] = 1 + i;
79  }
80 
81  // Get gamma parameter from session file.
82  ASSERTL0(m_session->DefinesParameter("Gamma"),
83  "Compressible flow sessions must define a Gamma parameter.");
84  m_session->LoadParameter("Gamma", m_gamma, 1.4);
85 
86  // Get E0 parameter from session file.
87  ASSERTL0(m_session->DefinesParameter("pInf"),
88  "Compressible flow sessions must define a pInf parameter.");
89  m_session->LoadParameter("pInf", m_pInf, 101325);
90 
91  // Get rhoInf parameter from session file.
92  ASSERTL0(m_session->DefinesParameter("rhoInf"),
93  "Compressible flow sessions must define a rhoInf parameter.");
94  m_session->LoadParameter("rhoInf", m_rhoInf, 1.225);
95 
96  // Get uInf parameter from session file.
97  ASSERTL0(m_session->DefinesParameter("uInf"),
98  "Compressible flow sessions must define a uInf parameter.");
99  m_session->LoadParameter("uInf", m_uInf, 0.1);
100 
101  m_UInf = m_uInf;
102 
103  // Get vInf parameter from session file.
104  if (m_spacedim == 2 || m_spacedim == 3)
105  {
106  ASSERTL0(m_session->DefinesParameter("vInf"),
107  "Compressible flow sessions must define a vInf parameter"
108  "for 2D/3D problems.");
109  m_session->LoadParameter("vInf", m_vInf, 0.0);
110  m_UInf = sqrt(m_uInf*m_uInf + m_vInf*m_vInf);
111  }
112 
113  // Get wInf parameter from session file.
114  if (m_spacedim == 3)
115  {
116  ASSERTL0(m_session->DefinesParameter("wInf"),
117  "Compressible flow sessions must define a wInf parameter"
118  "for 3D problems.");
119  m_session->LoadParameter("wInf", m_wInf, 0.0);
120  m_UInf = sqrt(m_uInf*m_uInf + m_vInf*m_vInf + m_wInf*m_wInf);
121  }
122 
123  m_session->LoadParameter ("GasConstant", m_gasConstant, 287.058);
124  m_session->LoadParameter ("Twall", m_Twall, 300.15);
125  m_session->LoadSolverInfo("ViscosityType", m_ViscosityType, "Constant");
126  m_session->LoadParameter ("mu", m_mu, 1.78e-05);
127  m_session->LoadParameter ("Skappa", m_Skappa, -2.048);
128  m_session->LoadParameter ("Kappa", m_Kappa, 0.0);
129  m_session->LoadParameter ("mu0", m_mu0, 1.0);
130  m_session->LoadParameter ("FL", m_FacL, 0.0);
131  m_session->LoadParameter ("FH", m_FacH, 0.0);
132  m_session->LoadParameter ("hFactor", m_hFactor, 1.0);
133  m_session->LoadParameter ("epsMax", m_eps_max, 1.0);
134  m_session->LoadParameter ("C1", m_C1, 3.0);
135  m_session->LoadParameter ("C2", m_C2, 5.0);
136  m_session->LoadSolverInfo("ShockCaptureType",
137  m_shockCaptureType, "Off");
138  m_session->LoadParameter ("thermalConductivity",
139  m_thermalConductivity, 0.0257);
140 
141  m_EqTypeStr = m_session->GetSolverInfo("EQTYPE");
142 
143  m_Cp = m_gamma / (m_gamma - 1.0) * m_gasConstant;
144  m_Prandtl = m_Cp * m_mu / m_thermalConductivity;
145 
146  m_session->LoadParameter("amplitude", m_amplitude, 0.001);
147  m_session->LoadParameter("omega", m_omega, 1.0);
148  m_session->LoadParameter("SteadyStateTol", m_steadyStateTol, 0.0);
149 
150  // Forcing terms for the sponge region
151  m_forcing = SolverUtils::Forcing::Load(m_session, m_fields,
152  m_fields.num_elements());
153 
154  // Loop over Boundary Regions for PressureOutflowFileBC
155  int nvariables = m_fields.num_elements();
156  Array<OneD, Array<OneD, NekDouble> > tmpStorage(nvariables);
157  for (int n = 0; n < m_fields[0]->GetBndConditions().num_elements(); ++n)
158  {
159  // PressureOutflowFile Boundary Condition
160  if (m_fields[0]->GetBndConditions()[n]->GetUserDefined() ==
161  "PressureOutflowFile")
162  {
163  int numBCPts = m_fields[0]->
164  GetBndCondExpansions()[n]->GetNpoints();
165  m_pressureStorage = Array<OneD, NekDouble>(numBCPts, 0.0);
166  for (int i = 0; i < nvariables; ++i)
167  {
168  tmpStorage[i] = Array<OneD, NekDouble>(numBCPts, 0.0);
169 
170  Vmath::Vcopy(
171  numBCPts,
172  m_fields[i]->GetBndCondExpansions()[n]->GetPhys(), 1,
173  tmpStorage[i], 1);
174  }
175  GetPressure(tmpStorage, m_pressureStorage);
176  }
177  }
178 
179  // Loop over Boundary Regions for PressureInflowFileBC
180  m_fieldStorage = Array<OneD, Array<OneD, NekDouble> > (nvariables);
181  for (int n = 0; n < m_fields[0]->GetBndConditions().num_elements(); ++n)
182  {
183  // PressureInflowFile Boundary Condition
184  if (m_fields[0]->GetBndConditions()[n]->GetUserDefined() ==
185  "PressureInflowFile")
186  {
187  int numBCPts = m_fields[0]->
188  GetBndCondExpansions()[n]->GetNpoints();
189  for (int i = 0; i < nvariables; ++i)
190  {
191  m_fieldStorage[i] = Array<OneD, NekDouble>(numBCPts, 0.0);
192  Vmath::Vcopy(
193  numBCPts,
194  m_fields[i]->GetBndCondExpansions()[n]->GetPhys(), 1,
195  m_fieldStorage[i], 1);
196  }
197  }
198  }
199 
200  // Type of advection class to be used
201  switch(m_projectionType)
202  {
203  // Continuous field
204  case MultiRegions::eGalerkin:
205  {
206  ASSERTL0(false, "Continuous field not supported.");
207  break;
208  }
209  // Discontinuous field
210  case MultiRegions::eDiscontinuous:
211  {
212  string advName, diffName, riemName;
213 
214  // Setting up advection and diffusion operators
215  m_session->LoadSolverInfo("AdvectionType", advName, "WeakDG");
216  m_session->LoadSolverInfo("DiffusionType", diffName, "LDGNS");
217 
218  m_advection = SolverUtils::GetAdvectionFactory()
219  .CreateInstance(advName, advName);
220  m_diffusion = SolverUtils::GetDiffusionFactory()
221  .CreateInstance(diffName, diffName);
222 
223  if (m_specHP_dealiasing)
224  {
225  m_advection->SetFluxVector(&CompressibleFlowSystem::
226  GetFluxVectorDeAlias, this);
227  m_diffusion->SetFluxVectorNS(
228  &CompressibleFlowSystem::GetViscousFluxVectorDeAlias,
229  this);
230  }
231  else
232  {
233  m_advection->SetFluxVector (&CompressibleFlowSystem::
234  GetFluxVector, this);
235  m_diffusion->SetFluxVectorNS(&CompressibleFlowSystem::
236  GetViscousFluxVector, this);
237  }
238 
239  if (m_shockCaptureType=="Smooth" && m_EqTypeStr=="EulerADCFE")
240  {
241  m_advection->SetFluxVector(&CompressibleFlowSystem::
242  GetFluxVector, this);
243 
244  m_diffusion->SetArtificialDiffusionVector(
245  &CompressibleFlowSystem::GetSmoothArtificialViscosity, this);
246  }
247  if (m_shockCaptureType=="NonSmooth" && m_EqTypeStr=="EulerADCFE")
248  {
249  m_advection->SetFluxVector(&CompressibleFlowSystem::
250  GetFluxVector, this);
251 
252  m_diffusion->SetArtificialDiffusionVector(
253  &CompressibleFlowSystem::GetArtificialDynamicViscosity, this);
254  }
255 
256  // Setting up Riemann solver for advection operator
257  m_session->LoadSolverInfo("UpwindType", riemName, "Average");
258 
259  m_riemannSolver = SolverUtils::GetRiemannSolverFactory()
260  .CreateInstance(riemName);
261 
262  // Setting up upwind solver for diffusion operator
263  m_riemannSolverLDG = SolverUtils::GetRiemannSolverFactory()
264  .CreateInstance("UpwindLDG");
265 
266  // Setting up parameters for advection operator Riemann solver
267  m_riemannSolver->SetParam (
268  "gamma", &CompressibleFlowSystem::GetGamma, this);
269  m_riemannSolver->SetAuxVec(
270  "vecLocs", &CompressibleFlowSystem::GetVecLocs, this);
271  m_riemannSolver->SetVector(
272  "N", &CompressibleFlowSystem::GetNormals, this);
273 
274  // Setting up parameters for diffusion operator Riemann solver
275  m_riemannSolverLDG->SetParam (
276  "gamma", &CompressibleFlowSystem::GetGamma, this);
277  m_riemannSolverLDG->SetVector(
278  "vecLocs", &CompressibleFlowSystem::GetVecLocs, this);
279  m_riemannSolverLDG->SetVector(
280  "N", &CompressibleFlowSystem::GetNormals, this);
281 
282  // Concluding initialisation of advection / diffusion operators
283  m_advection->SetRiemannSolver (m_riemannSolver);
284  m_diffusion->SetRiemannSolver (m_riemannSolverLDG);
285  m_advection->InitObject (m_session, m_fields);
286  m_diffusion->InitObject (m_session, m_fields);
287  break;
288  }
289  default:
290  {
291  ASSERTL0(false, "Unsupported projection type.");
292  break;
293  }
294  }
295  }
ASSERTL0
#define ASSERTL0(condition, msg)
Definition: ErrorUtil.hpp:161
Nektar::CompressibleFlowSystem::m_fieldStorage
Array< OneD, Array< OneD, NekDouble > > m_fieldStorage
Definition: CompressibleFlowSystem.h:132
Nektar::SolverUtils::UnsteadySystem::m_homoInitialFwd
bool m_homoInitialFwd
Flag to determine if simulation should start in homogeneous forward transformed state.
Definition: UnsteadySystem.h:80
Nektar::LibUtilities::NekFactory::CreateInstance
tBaseSharedPtr CreateInstance(tKey idKey BOOST_PP_COMMA_IF(MAX_PARAM) BOOST_PP_ENUM_BINARY_PARAMS(MAX_PARAM, tParam, x))
Create an instance of the class referred to by idKey.
Definition: NekFactory.hpp:162
Nektar::CompressibleFlowSystem::GetViscousFluxVector
void GetViscousFluxVector(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &derivatives, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &viscousTensor)
Return the flux vector for the LDG diffusion problem.
Definition: CompressibleFlowSystem.cpp:1792
Nektar::CompressibleFlowSystem::m_riemannSolverLDG
SolverUtils::RiemannSolverSharedPtr m_riemannSolverLDG
Definition: CompressibleFlowSystem.h:80
Nektar::SolverUtils::GetDiffusionFactory
DiffusionFactory & GetDiffusionFactory()
Definition: Diffusion.cpp:42
Nektar::SolverUtils::EquationSystem::m_projectionType
enum MultiRegions::ProjectionType m_projectionType
Type of projection; e.g continuous or discontinuous.
Definition: EquationSystem.h:514
Nektar::SolverUtils::EquationSystem::m_specHP_dealiasing
bool m_specHP_dealiasing
Flag to determine if dealisising is usde for the Spectral/hp element discretisation.
Definition: EquationSystem.h:512
Nektar::CompressibleFlowSystem::GetArtificialDynamicViscosity
void GetArtificialDynamicViscosity(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &mu_var)
Nektar::SolverUtils::Forcing::Load
static SOLVER_UTILS_EXPORT std::vector< ForcingSharedPtr > Load(const LibUtilities::SessionReaderSharedPtr &pSession, const Array< OneD, MultiRegions::ExpListSharedPtr > &pFields, const unsigned int &pNumForcingFields=0)
Definition: Forcing.cpp:84
Nektar::CompressibleFlowSystem::m_vecLocs
Array< OneD, Array< OneD, NekDouble > > m_vecLocs
Definition: CompressibleFlowSystem.h:83
Nektar::CompressibleFlowSystem::GetViscousFluxVectorDeAlias
void GetViscousFluxVectorDeAlias(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &derivatives, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &viscousTensor)
Return the flux vector for the LDG diffusion problem.
Definition: CompressibleFlowSystem.cpp:2125
Nektar::CompressibleFlowSystem::GetVecLocs
const Array< OneD, const Array< OneD, NekDouble > > & GetVecLocs()
Definition: CompressibleFlowSystem.h:285
Nektar::CompressibleFlowSystem::GetFluxVectorDeAlias
void GetFluxVectorDeAlias(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &flux)
Return the flux vector for the compressible Euler equations by using the de-aliasing technique...
Definition: CompressibleFlowSystem.cpp:1701
Nektar::SolverUtils::GetRiemannSolverFactory
RiemannSolverFactory & GetRiemannSolverFactory()
Definition: RiemannSolver.cpp:63
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::SolverUtils::GetAdvectionFactory
AdvectionFactory & GetAdvectionFactory()
Gets the factory for initialising advection objects.
Definition: Advection.cpp:46
Nektar::CompressibleFlowSystem::m_pressureStorage
Array< OneD, NekDouble > m_pressureStorage
Definition: CompressibleFlowSystem.h:129
Nektar::CompressibleFlowSystem::m_advection
SolverUtils::AdvectionSharedPtr m_advection
Definition: CompressibleFlowSystem.h:81
Nektar::CompressibleFlowSystem::m_diffusion
SolverUtils::DiffusionSharedPtr m_diffusion
Definition: CompressibleFlowSystem.h:82
Nektar::CompressibleFlowSystem::GetNormals
const Array< OneD, const Array< OneD, NekDouble > > & GetNormals()
Definition: CompressibleFlowSystem.h:290
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Nektar::SolverUtils::EquationSystem::m_session
LibUtilities::SessionReaderSharedPtr m_session
The session reader.
Definition: EquationSystem.h:452
Nektar::CompressibleFlowSystem::GetSmoothArtificialViscosity
void GetSmoothArtificialViscosity(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, NekDouble > &eps_bar)
Nektar::SolverUtils::EquationSystem::GetPressure
SOLVER_UTILS_EXPORT MultiRegions::ExpListSharedPtr GetPressure()
Get pressure field if available.
Definition: EquationSystem.h:750
Nektar::CompressibleFlowSystem::m_riemannSolver
SolverUtils::RiemannSolverSharedPtr m_riemannSolver
Definition: CompressibleFlowSystem.h:79
Nektar::CompressibleFlowSystem::GetFluxVector
void GetFluxVector(const Array< OneD, Array< OneD, NekDouble > > &physfield, Array< OneD, Array< OneD, Array< OneD, NekDouble > > > &flux)
Return the flux vector for the compressible Euler equations.
Definition: CompressibleFlowSystem.cpp:1638
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
Nektar::CompressibleFlowSystem::m_forcing
std::vector< SolverUtils::ForcingSharedPtr > m_forcing
Definition: CompressibleFlowSystem.h:122
virtual bool Nektar::CompressibleFlowSystem::v_PostIntegrate ( int  step)
protectedvirtual

Reimplemented from Nektar::SolverUtils::UnsteadySystem.

virtual void Nektar::CompressibleFlowSystem::v_SetInitialConditions ( NekDouble  initialtime = 0.0,
bool  dumpInitialConditions = true,
const int  domain = 0 
)
protectedvirtual

Set the physical fields based on a restart file, or a function describing the initial condition given in the session.

Parameters
initialtimeTime at which to evaluate the function.
dumpInitialConditionsWrite the initial condition to file?

Reimplemented from Nektar::SolverUtils::EquationSystem.

Reimplemented in Nektar::EulerADCFE, Nektar::EulerCFE, and Nektar::NavierStokesCFE.

Referenced by Nektar::NavierStokesCFE::v_SetInitialConditions(), Nektar::EulerCFE::v_SetInitialConditions(), and Nektar::EulerADCFE::v_SetInitialConditions().

void Nektar::CompressibleFlowSystem::WallBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Wall boundary conditions for compressible flow problems.

Definition at line 399 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_spacedim, Nektar::SolverUtils::EquationSystem::m_traceNormals, Vmath::Smul(), Vmath::Vcopy(), Vmath::Vsub(), and Vmath::Vvtvp().

Referenced by SetCommonBC().

403  {
404  int i;
405  int nTracePts = GetTraceTotPoints();
406  int nVariables = physarray.num_elements();
407 
408  const Array<OneD, const int> &traceBndMap
409  = m_fields[0]->GetTraceBndMap();
410 
411  // Get physical values of the forward trace
412  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
413  for (i = 0; i < nVariables; ++i)
414  {
415  Fwd[i] = Array<OneD, NekDouble>(nTracePts);
416  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
417  }
418 
419  // Adjust the physical values of the trace to take
420  // user defined boundaries into account
421  int e, id1, id2, nBCEdgePts, eMax;
422 
423  eMax = m_fields[0]->GetBndCondExpansions()[bcRegion]->GetExpSize();
424 
425  for (e = 0; e < eMax; ++e)
426  {
427  nBCEdgePts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
428  GetExp(e)->GetTotPoints();
429  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
430  GetPhys_Offset(e);
431  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
432 
433  // Boundary condition for epsilon term.
434  if (nVariables == m_spacedim+3)
435  {
436  NekDouble factor = 1.0;
437  NekDouble factor2 = 1.0;
438 
439  Array<OneD, NekDouble > tmp2(nBCEdgePts, 0.0);
440  Vmath::Smul(nBCEdgePts,
441  factor,
442  &Fwd[nVariables-1][id2], 1,
443  &tmp2[0], 1);
444 
445  Vmath::Vsub(nBCEdgePts,
446  &Fwd[nVariables-1][id2], 1,
447  &tmp2[0], 1,
448  &Fwd[nVariables-1][id2], 1);
449 
450  Vmath::Smul(nBCEdgePts,
451  factor2,
452  &Fwd[nVariables-1][id2], 1,
453  &Fwd[nVariables-1][id2], 1);
454 
455  }
456 
457  // For 2D/3D, define: v* = v - 2(v.n)n
458  Array<OneD, NekDouble> tmp(nBCEdgePts, 0.0);
459 
460  // Calculate (v.n)
461  for (i = 0; i < m_spacedim; ++i)
462  {
463  Vmath::Vvtvp(nBCEdgePts,
464  &Fwd[1+i][id2], 1,
465  &m_traceNormals[i][id2], 1,
466  &tmp[0], 1,
467  &tmp[0], 1);
468  }
469 
470  // Calculate 2.0(v.n)
471  Vmath::Smul(nBCEdgePts, -2.0, &tmp[0], 1, &tmp[0], 1);
472 
473  // Calculate v* = v - 2.0(v.n)n
474  for (i = 0; i < m_spacedim; ++i)
475  {
476  Vmath::Vvtvp(nBCEdgePts,
477  &tmp[0], 1,
478  &m_traceNormals[i][id2], 1,
479  &Fwd[1+i][id2], 1,
480  &Fwd[1+i][id2], 1);
481  }
482 
483  // Copy boundary adjusted values into the boundary expansion
484  for (i = 0; i < nVariables; ++i)
485  {
486  Vmath::Vcopy(nBCEdgePts, &Fwd[i][id2], 1,
487  &(m_fields[i]->GetBndCondExpansions()[bcRegion]->
488  UpdatePhys())[id1], 1);
489  }
490  }
491  }
Vmath::Vvtvp
void Vvtvp(int n, const T *w, const int incw, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
vvtvp (vector times vector plus vector): z = w*x + y
Definition: Vmath.cpp:428
Nektar::SolverUtils::EquationSystem::m_traceNormals
Array< OneD, Array< OneD, NekDouble > > m_traceNormals
Array holding trace normals for DG simulations in the forwards direction.
Definition: EquationSystem.h:516
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Vmath::Vsub
void Vsub(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Subtract vector z = x-y.
Definition: Vmath.cpp:329
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047
void Nektar::CompressibleFlowSystem::WallViscousBC ( int  bcRegion,
int  cnt,
Array< OneD, Array< OneD, NekDouble > > &  physarray 
)
protected

Wall boundary conditions for viscous compressible flow problems.

Definition at line 496 of file CompressibleFlowSystem.cpp.

References Nektar::SolverUtils::EquationSystem::GetPhys_Offset(), Nektar::SolverUtils::EquationSystem::GetTraceTotPoints(), Nektar::SolverUtils::EquationSystem::m_fields, Nektar::SolverUtils::EquationSystem::m_spacedim, Vmath::Neg(), Vmath::Smul(), Vmath::Vcopy(), and Vmath::Vsub().

Referenced by SetCommonBC().

500  {
501  int i;
502  int nTracePts = GetTraceTotPoints();
503  int nVariables = physarray.num_elements();
504 
505  const Array<OneD, const int> &traceBndMap
506  = m_fields[0]->GetTraceBndMap();
507 
508  // Get physical values of the forward trace
509  Array<OneD, Array<OneD, NekDouble> > Fwd(nVariables);
510  for (i = 0; i < nVariables; ++i)
511  {
512  Fwd[i] = Array<OneD, NekDouble>(nTracePts);
513  m_fields[i]->ExtractTracePhys(physarray[i], Fwd[i]);
514  }
515 
516  // Take into account that for PDE based shock capturing, eps = 0 at the
517  // wall. Adjust the physical values of the trace to take user defined
518  // boundaries into account
519  int e, id1, id2, nBCEdgePts, eMax;
520 
521  eMax = m_fields[0]->GetBndCondExpansions()[bcRegion]->GetExpSize();
522 
523  for (e = 0; e < eMax; ++e)
524  {
525  nBCEdgePts = m_fields[0]->GetBndCondExpansions()[bcRegion]->
526  GetExp(e)->GetTotPoints();
527  id1 = m_fields[0]->GetBndCondExpansions()[bcRegion]->
528  GetPhys_Offset(e);
529  id2 = m_fields[0]->GetTrace()->GetPhys_Offset(traceBndMap[cnt+e]);
530 
531  if (nVariables == m_spacedim+3)
532  {
533  NekDouble factor = 0.0;
534  NekDouble factor2 = 1.0;
535 
536  Array<OneD, NekDouble > tmp2(nBCEdgePts, 0.0);
537  Vmath::Smul(nBCEdgePts,
538  factor,
539  &Fwd[nVariables-1][id2], 1,
540  &tmp2[0], 1);
541 
542  Vmath::Vsub(nBCEdgePts,
543  &Fwd[nVariables-1][id2], 1,
544  &tmp2[0], 1,
545  &Fwd[nVariables-1][id2], 1);
546 
547  Vmath::Smul(nBCEdgePts,
548  factor2,
549  &Fwd[nVariables-1][id2], 1,
550  &Fwd[nVariables-1][id2], 1);
551  }
552 
553  for (i = 0; i < m_spacedim; i++)
554  {
555  Vmath::Neg(nBCEdgePts, &Fwd[i+1][id2], 1);
556  }
557 
558  // Copy boundary adjusted values into the boundary expansion
559  for (i = 0; i < nVariables; ++i)
560  {
561  Vmath::Vcopy(nBCEdgePts, &Fwd[i][id2], 1,
562  &(m_fields[i]->GetBndCondExpansions()[bcRegion]->
563  UpdatePhys())[id1], 1);
564  }
565  }
566  }
Vmath::Smul
void Smul(int n, const T alpha, const T *x, const int incx, T *y, const int incy)
Scalar multiply y = alpha*y.
Definition: Vmath.cpp:199
Nektar::SolverUtils::EquationSystem::m_spacedim
int m_spacedim
Spatial dimension (>= expansion dim).
Definition: EquationSystem.h:492
Vmath::Neg
void Neg(int n, T *x, const int incx)
Negate x = -x.
Definition: Vmath.cpp:382
Nektar::NekDouble
double NekDouble
Definition: NektarUnivTypeDefs.hpp:44
Vmath::Vsub
void Vsub(int n, const T *x, const int incx, const T *y, const int incy, T *z, const int incz)
Subtract vector z = x-y.
Definition: Vmath.cpp:329
Nektar::SolverUtils::EquationSystem::GetTraceTotPoints
SOLVER_UTILS_EXPORT int GetTraceTotPoints()
Definition: EquationSystem.h:843
Nektar::SolverUtils::EquationSystem::GetPhys_Offset
SOLVER_UTILS_EXPORT int GetPhys_Offset(int n)
Definition: EquationSystem.h:858
Nektar::SolverUtils::EquationSystem::m_fields
Array< OneD, MultiRegions::ExpListSharedPtr > m_fields
Array holding all dependent variables.
Definition: EquationSystem.h:460
Vmath::Vcopy
void Vcopy(int n, const T *x, const int incx, T *y, const int incy)
Definition: Vmath.cpp:1047

Friends And Related Function Documentation

friend class MemoryManager< CompressibleFlowSystem >
friend

Definition at line 56 of file CompressibleFlowSystem.h.

Member Data Documentation

string Nektar::CompressibleFlowSystem::className
static
Initial value:
=
SolverUtils::GetEquationSystemFactory().RegisterCreatorFunction(
"CompressibleFlowSystem",
CompressibleFlowSystem::create,
"Auxiliary functions for the compressible flow system.")

Name of class.

Definition at line 66 of file CompressibleFlowSystem.h.

SolverUtils::AdvectionSharedPtr Nektar::CompressibleFlowSystem::m_advection
protected

Definition at line 81 of file CompressibleFlowSystem.h.

Referenced by Nektar::NavierStokesCFE::DoOdeRhs(), Nektar::EulerCFE::DoOdeRhs(), Nektar::EulerADCFE::DoOdeRhs(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_amplitude
protected

Definition at line 109 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_C1
protected

Definition at line 105 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_C2
protected

Definition at line 106 of file CompressibleFlowSystem.h.

Referenced by Nektar::EulerADCFE::DoOdeRhs(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_Cp
protected

Definition at line 104 of file CompressibleFlowSystem.h.

Referenced by GetViscousFluxVector(), and v_InitObject().

SolverUtils::DiffusionSharedPtr Nektar::CompressibleFlowSystem::m_diffusion
protected

Definition at line 82 of file CompressibleFlowSystem.h.

Referenced by Nektar::NavierStokesCFE::DoOdeRhs(), Nektar::EulerADCFE::DoOdeRhs(), Nektar::EulerADCFE::v_InitObject(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_eps_max
protected

Definition at line 102 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

std::string Nektar::CompressibleFlowSystem::m_EqTypeStr
protected

Definition at line 95 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

std::ofstream Nektar::CompressibleFlowSystem::m_errFile
protected

Definition at line 113 of file CompressibleFlowSystem.h.

NekDouble Nektar::CompressibleFlowSystem::m_FacH
protected

Definition at line 101 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_FacL
protected

Definition at line 100 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

Array<OneD, Array<OneD, NekDouble> > Nektar::CompressibleFlowSystem::m_fieldStorage
protected

Definition at line 132 of file CompressibleFlowSystem.h.

Referenced by PressureInflowFileBC(), and v_InitObject().

std::vector<SolverUtils::ForcingSharedPtr> Nektar::CompressibleFlowSystem::m_forcing
protected

Definition at line 122 of file CompressibleFlowSystem.h.

Referenced by Nektar::NavierStokesCFE::DoOdeRhs(), Nektar::EulerCFE::DoOdeRhs(), Nektar::EulerADCFE::DoOdeRhs(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_gamma
protected

Definition at line 84 of file CompressibleFlowSystem.h.

Referenced by Nektar::EulerCFE::EvaluateIsentropicVortex(), Nektar::EulerCFE::GetExactRinglebFlow(), GetGamma(), GetPressure(), PressureInflowFileBC(), PressureOutflowBC(), PressureOutflowFileBC(), PressureOutflowNonReflectiveBC(), RiemannInvariantBC(), Nektar::EulerCFE::SetBoundaryRinglebFlow(), Nektar::EulerCFE::SetInitialRinglebFlow(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_gasConstant
protected

Definition at line 91 of file CompressibleFlowSystem.h.

Referenced by GetGasConstant(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_hFactor
protected

Definition at line 107 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_Kappa
protected

Definition at line 98 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_mu
protected

Definition at line 96 of file CompressibleFlowSystem.h.

Referenced by GetViscousFluxVector(), GetViscousFluxVectorDeAlias(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_mu0
protected

Definition at line 99 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_omega
protected

Definition at line 110 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

StdRegions::StdHexExpSharedPtr Nektar::CompressibleFlowSystem::m_OrthoHexExp
protected

Definition at line 124 of file CompressibleFlowSystem.h.

StdRegions::StdQuadExpSharedPtr Nektar::CompressibleFlowSystem::m_OrthoQuadExp
protected

Definition at line 123 of file CompressibleFlowSystem.h.

NekDouble Nektar::CompressibleFlowSystem::m_pInf
protected

Definition at line 85 of file CompressibleFlowSystem.h.

Referenced by PressureOutflowBC(), PressureOutflowNonReflectiveBC(), RiemannInvariantBC(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_Prandtl
protected

Definition at line 108 of file CompressibleFlowSystem.h.

Referenced by GetViscousFluxVector(), and v_InitObject().

Array<OneD, NekDouble> Nektar::CompressibleFlowSystem::m_pressureStorage
protected

Definition at line 129 of file CompressibleFlowSystem.h.

Referenced by PressureOutflowFileBC(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_rhoInf
protected

Definition at line 86 of file CompressibleFlowSystem.h.

Referenced by RiemannInvariantBC(), and v_InitObject().

SolverUtils::RiemannSolverSharedPtr Nektar::CompressibleFlowSystem::m_riemannSolver
protected

Definition at line 79 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

SolverUtils::RiemannSolverSharedPtr Nektar::CompressibleFlowSystem::m_riemannSolverLDG
protected

Definition at line 80 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

std::string Nektar::CompressibleFlowSystem::m_shockCaptureType
protected

Definition at line 94 of file CompressibleFlowSystem.h.

Referenced by Nektar::EulerADCFE::DoOdeRhs(), Nektar::EulerADCFE::v_InitObject(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_Skappa
protected

Definition at line 97 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

bool Nektar::CompressibleFlowSystem::m_smoothDiffusion
protected

Definition at line 125 of file CompressibleFlowSystem.h.

Referenced by Nektar::EulerADCFE::v_InitObject().

int Nektar::CompressibleFlowSystem::m_steadyStateSteps
protected

Definition at line 116 of file CompressibleFlowSystem.h.

NekDouble Nektar::CompressibleFlowSystem::m_steadyStateTol
protected

Definition at line 119 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_thermalConductivity
protected

Definition at line 103 of file CompressibleFlowSystem.h.

Referenced by GetViscousFluxVector(), GetViscousFluxVectorDeAlias(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_Twall
protected

Definition at line 92 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_uInf
protected

Definition at line 87 of file CompressibleFlowSystem.h.

Referenced by PressureInflowFileBC(), PressureOutflowBC(), PressureOutflowFileBC(), PressureOutflowNonReflectiveBC(), RiemannInvariantBC(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_UInf
protected

Definition at line 90 of file CompressibleFlowSystem.h.

Referenced by v_InitObject().

Array<OneD, Array<OneD, NekDouble> > Nektar::CompressibleFlowSystem::m_un
protected

Definition at line 135 of file CompressibleFlowSystem.h.

Array<OneD, Array<OneD, NekDouble> > Nektar::CompressibleFlowSystem::m_vecLocs
protected

Definition at line 83 of file CompressibleFlowSystem.h.

Referenced by GetVecLocs(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_vInf
protected

Definition at line 88 of file CompressibleFlowSystem.h.

Referenced by PressureInflowFileBC(), PressureOutflowBC(), PressureOutflowFileBC(), PressureOutflowNonReflectiveBC(), RiemannInvariantBC(), and v_InitObject().

std::string Nektar::CompressibleFlowSystem::m_ViscosityType
protected

Definition at line 93 of file CompressibleFlowSystem.h.

Referenced by GetViscousFluxVector(), GetViscousFluxVectorDeAlias(), and v_InitObject().

NekDouble Nektar::CompressibleFlowSystem::m_wInf
protected

Definition at line 89 of file CompressibleFlowSystem.h.

Referenced by PressureInflowFileBC(), PressureOutflowBC(), PressureOutflowFileBC(), PressureOutflowNonReflectiveBC(), RiemannInvariantBC(), and v_InitObject().

Generated on Wed Mar 23 2016 20:14:27 for Nektar++ by   doxygen 1.8.8